基于改进Jaya算法和组合相关函数的结构损伤识别
2023-10-31张广才赵文龙万春风
张广才, 赵文龙, 万春风
(东南大学 混凝土及预应力混凝土结构教育部重点实验室,南京 211189)
重大工程结构,如大跨空间结构、超高层建筑、大跨径桥梁、海上采油平台、大型水坝,设计使用寿命长达几十年甚至上百年。长期服役期间,因地震、台风、洪水等自然灾害,以及环境侵蚀、材料老化、锈蚀、超载等不利因素的耦合作用,结构承力构件易出现裂缝、疲劳、脱落等损伤,如未能及时发现并修复,损伤逐渐累积可能导致结构整体坍塌,引发灾难性事故[1]。因此,为保证结构使用安全、减少运维成本,进行连续结构健康监测和损伤识别研究具有重要的理论和现实意义。
经过几十年的发展,国内外学者已提出了一系列损伤识别方法,其中基于振动测试的结构损伤识别方法利用预安装在结构上的传感器测量位移、速度、加速度、应变等动态响应,反向识别出结构刚度、质量、阻尼等物理特性的变化进而判断结构损伤情况,已取得丰硕的研究成果。基于振动测试的损伤识别方法可大致分为传统方法和非传统方法,传统方法主要包括基于固有频率、模态振型、模态应变能、曲率模态、传递率函数、扩展卡尔曼滤波、响应灵敏度、小波分析等方法[2-9],但存在对小损伤不敏感、对局部损伤不敏感、需要较多传感器、噪声鲁棒性差等缺点。随着软计算方法的发展,基于神经网络和群智能优化算法的非传统识别方法受到越来越多关注。神经网络具有较强的并行计算、自我学习、非线性映射能力和鲁棒性,但需要大量的训练样本,计算效率低。群智能优化算法,如遗传算法、粒子群优化算法、蚁狮优化算法、布谷鸟搜索、树种算法、鲸鱼算法等[10-15],因搜索能力强,易于实施,且不需要已知较好的初始值和梯度信息等优点被广泛研究和应用。然而,以上群智能优化算法需要设置特定于算法的参数,而这些参数会影响算法的有效性,如算法参数设置不当将可能增加计算成本甚至陷入局部最优解。为此,Rao[16]提出一种无特定参数的优化算法,命名为Jaya算法,其核心思想在于子代个体向最优解移动同时远离最差解,进而不断提高解的质量,已应用于电气工程、机械设计、热工程、结构工程等领域[17-20]。虽然Jaya算法在标准函数测试以及若干工程优化设计中表现出比遗传算法,粒子群算法,教学优化算法、人工蜂群算法等智能算法更优的性能,但Jaya算法仍然存在收敛速度慢、易陷入局部最优而提前收敛等问题[21]。为提高算法性能,在传统Jaya算法基础上引入三种新的策略得到改进Jaya(improved Jaya, I-Jaya)算法。首先,Hammersley序列初始化种群,使初始种群均匀覆盖整个搜索空间,增加种群的多样性;其次,引入Lévy飞行机制在最优解附近随机搜索,提高最优解的质量以逃离局部最优;最后,引入经验学习策略提高全局搜索能力,更好的平衡全局搜索和局部搜索。
加速度是较容易获取的动力响应之一,且含有丰富的结构损伤信息。作用在工程结构上的随机激励,如风荷载和交通荷载,往往难以准确获取,因此,利用未知随机激励下工程结构的加速度响应识别损伤更符合其实际服役状态,具有重要的研究意义。Li等[22]提出加速度的自/互相相关矩阵的协方差,识别白噪声激励下结构的局部刚度损伤。Ni等[23]利用多个测点的加速度响应构造自相关、互相关函数,成功识别未知随机激励下的结构损伤。在此基础上,Wang等[24]将四种优化算法与加速度互相关函数结合成功识别结构参数。然而,以上研究均需要定义参考点,如果参考点处加速度响应的测量精度差可能会影响互相关函数的识别效果,甚至得到错误的识别结果[25]。针对此问题,本文提出组合相关函数的方法,计算加速度互相关函数的组合,该方法不需要定义参考点。
本文首先介绍Jaya算法的基本原理和实现流程;然后,将Hammersley序列初始化、Lévy飞行搜索、经验学习策略,引入Jaya得到改进Jaya算法;其次,提出组合相关函数,并介绍了损伤识别的步骤;最后,采用白噪声激励下多自由度体系算例验证基于改进Jaya算法和组合相关函数的损伤识别方法的有效性,并详细讨论了噪声等级、采样频率、采样时间、数据点数、传感器数量、模型误差等因素对损伤识别结果的影响
1 优化算法
1.1 Jaya算法
Jaya算法是近年新提出的一种基于全局搜索的群智能优化算法,用于求解约束和无约束优化问题。该算法的显著特点是无算法控制参数,仅需要设置种群规模和最大迭代次数,这极大提高了优化算法的计算效率。Jaya算法可大致分为初始化种群、更新个体、贪婪选择和输出最优解4个部分。
(1)初始化种群:Jaya算法在搜索空间内随机生成初始种群Xi,j
(1)
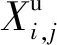
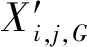
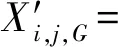
rand2×(Xworst,j,G-|Xi,j,G|)
(2)
式中:Xi,j,G和|Xi,j,G|分别为在第G次迭代时第i个体的第j维变量及其绝对值;rand1和rand2为[0, 1]均匀分布的随机数;Xbest,j,G和Xworst,j,G分别为第G次迭代时最优解和最差解的第j维变量值;等号右侧第二项rand1×(Xbest,j,G-|Xi,j,G|)为个体朝向最优解移动,第三项rand2×(Xworst,j,G-|Xi,j,G|)为个体远离最差解。
(3)贪婪选择:比较更新前后的解Xi,G和X′i,G,选择适应性更优的解存活到下一代
(3)
式中:Xi,G+1和Xi,G分别为第G+1和第G次迭代时的第i个体;X′i,G为Xi,G迭代更新后的个体;f(Xi,G)和f(X′i,G)分别为Xi,G更新前后的适应性值。
(4)输出最优解:重复更新个体和贪婪选择直到达到最大迭代次数或满足收敛条件,输出识别的最优解。
1.2 改进Jaya算法
1.2.1 Hammersley序列初始化
Jaya算法在给定搜索空间内随机生成个体,操作简单、易于实现,但存在明显的不稳定性。如果初始种群同时分布在有限的局部区域,后续迭代更新的个体将限制在一定范围内,这可能导致优化算法陷入局部最优解。为了增加种群的多样性和算法的遍历性,使用低差异序列初始化Jaya算法。与伪随机数相比,低差异序列可以在高维空间生成更加均匀的样本。Hammersley序列是一种被广泛应用的低差异序列,该序列利用计算机二进制表示的特性,将给定十进制数的二进制表示镜像到小数点后,并构造一个介于[0, 1]的值,其主要步骤如下:
步骤1任意一个自然数n都可以表示为基数P的数位和形式
(4)
式中,m=[logp(n)],[]为提取内部数字的整数部分。
步骤2将式(4)中的系数{nm,…,n1,n0}反序排列,并放在小数点后,其值可表示为
步骤3自然数n在k维空间的Hammersley序列为
ψk(n)=(n/N,φP1(n),φP2(n),…,φPk-1(n))
(6)
式中:n=0,1,…,N-1;N为生成的样本点数目;P1,P2,…,Pk-1为质数。
由Logistics映射、Tent映射、Random序列和Hammersley序列四种初始化方法生成100个样本点的统计结果,如图1所示。由图1可以发现,Logistics和Tent映射生成的点在局部区域过于稀疏或集中,而Hammersley序列在搜索空间内生成均匀的样本点,因此利用该序列初始化种群能够使初始种群均匀覆盖整个搜索空间,有利于提高算法的种群多样性。
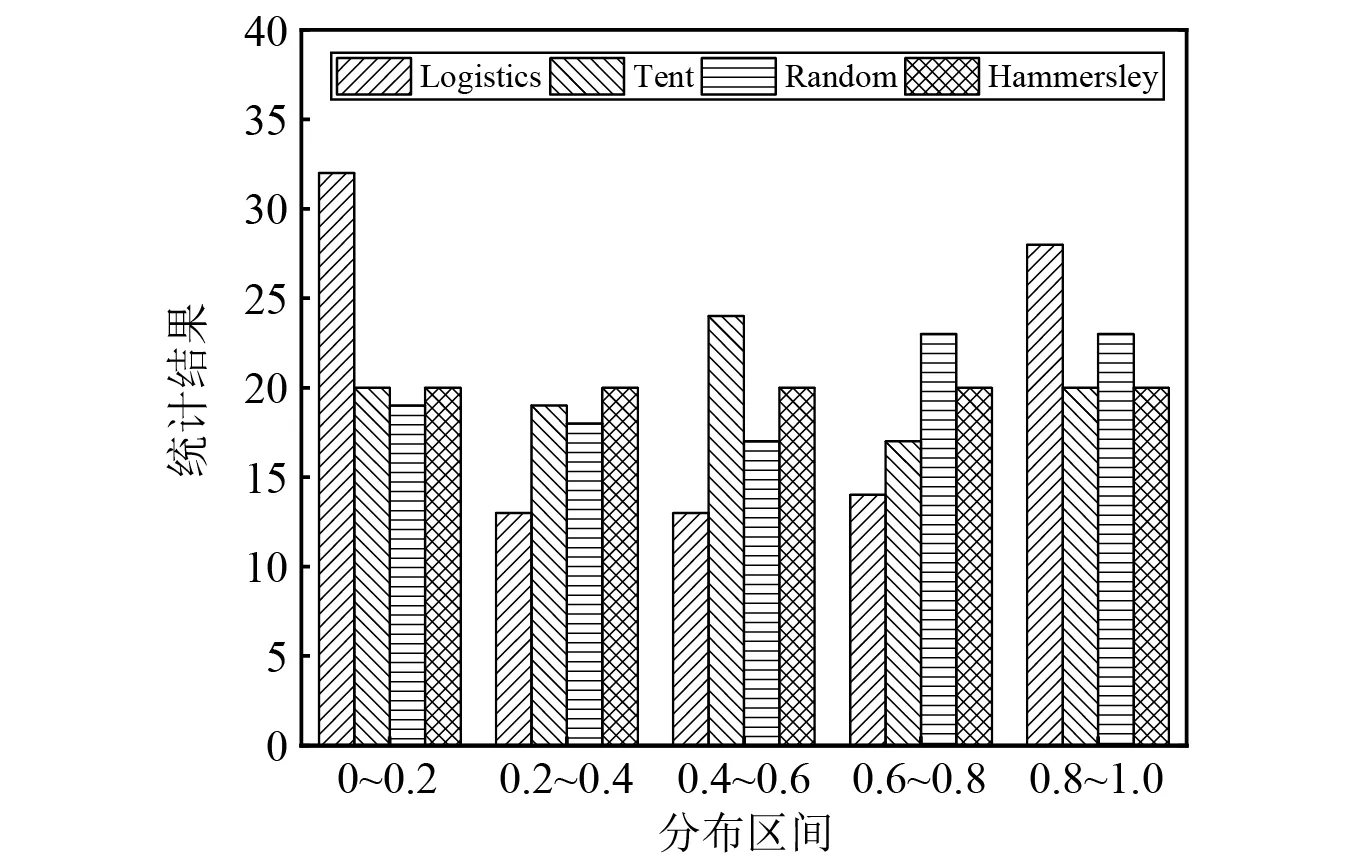
图1 四种初始化方法生成100个样本点的统计结果
使用Hammersley序列初始化种群时,在搜索空间内映射生成np个个体,映射方法为
(7)
式中,ψ(i,j)为Hammersley序列生成的样本点。
1.2.2 Lévy飞行搜索
Lévy飞行是一种随机搜索的非高斯随机过程,其步长符合莱维分布。由式(2)可知,Jaya算法的最优解引导其他个体向其位置移动,在搜索过程中起着重要作用。然而,求解复杂的多峰值优化问题时,最优个体可能陷于局部最优区域,此时种群内的其他个体易被吸引到该区域,导致陷入局部最优解而过早收敛。为此,将Lévy飞行与Jaya算法结合,在最优解附近随机搜索,充分发挥Lévy飞行强大的搜索能力,有利于增大搜索范围以跳出局部最优点。
种群内某一个体Xi通过Lévy飞行生成新的个体Xi+1
Xi+1=Xi+κ⊕L(λ)
(8)
式中:κ为步长控制参数;⊕为点对点乘法;λ为莱维分布指数,0<λ≤2。
步长step的计算方式为
(9)
式中:Xbest为当前迭代的最优解;Xr为种群内随机选择的个体但与最优解不同;u和v服从正态分布,表达式为
(10)
式中,σu和σv的取值分别为
(11)
式中,Γ为Gamma函数。
最优解Xbest的更新方式为
(12)
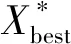
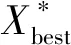
1.2.3 经验学习策略
Jaya算法同时考虑全局最优解和最差解更新种群个体,虽然可以加快算法的收敛速度,提高局部搜索能力,但种群多样性和全局搜索能力可能会随着收敛速度的加快而下降。为了提高种群多样性和全局搜索能力,引入一种基于种群内其他个体信息的经验学习策略。具体而言,从种群内随机选择另外两个不同个体Xk和Xl,然后利用其差值确定的搜索方向来更新当前个体Xi
(13)
式中:Xp,j和Xq,j分别为第p和第q个个体的第j维变量;rand为区间[0, 1]的随机数。
引入Hammersley序列初始化、Lévy飞行搜索、经验学习策略,得到改进Jaya算法,流程图如图2所示。以上改进机制没有添加任何新的算法参数,即I-Jaya算法不需要设置任何特定于算法的参数,结构清晰、易于操作。
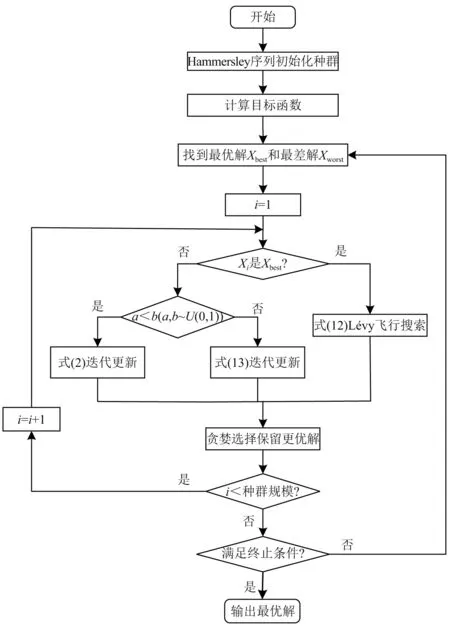
图2 I-Jaya算法流程图
2 组合相关函数
N自由度线性结构体系在外荷载激励下的运动方程为
(14)
假设结构的初始位移和速度为0,则荷载激励下该结构的第μ自由度的加速度响应为
(15)
(16)
结构上任意两自由度μ和ς之间的加速度互相关函数为
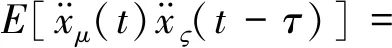
E[F(μ1)F(μ2)]dμ1dμ2
(17)
式中:μ1和μ2为很小的时间间隔;E[F(μ1)F(μ2)]=Sδ(μ1-μ2),当μ1=μ2时
(18)
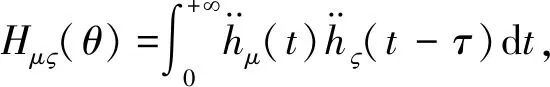
如结构上同时布置n个测点,则以某一测点w为参考点的加速度互相关函数Rw为
Rw=[Rw,1,Rw,2,…,Rw,n]
(19)
如不指定某一测点为参考点,计算加速度响应互相关函数的组合,得到无参考点的组合相关函数R
R=[R1,2,R1,3,…,R1,n,R2,3,…,R2,n,…,Rn-1,n]
(20)
3 损伤识别步骤
采用折减单元刚度模拟结构的局部损伤,引入损伤因子αe(e=1,2,…,ne)
(21)
本文提出基于I-Jaya算法和组合相关函数的损伤识别方法,大致步骤如下:
步骤1引入结构刚度损伤,测量未知随机激励下损伤结构的加速度响应,然后由式(20)计算所有加速度互相关函数的组合,得到测量值的组合相关函数Rmea。
步骤2利用I-Jaya算法中的Hammersley序列初始化种群,得到初始结构参数。
步骤3对初始种群内的个体计算目标函数obj
(22)
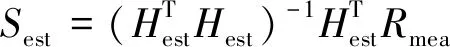
步骤4确定全局最优解Xbest和最差解Xworst,并利用I-Jaya算法迭代更新结构参数θ,使组合相关函数Rmea和Rest尽可能接近。
步骤5重复步骤3、步骤4直到达到最大迭代次数或满足其他终止条件,输出最优结构参数,得到结构损伤位置和程度。
4 算例验证
采用10自由度结构体系验证基于I-Jaya算法和组合相关函数的结构损伤识别方法的有效性,并对优化算法、噪声等级、采样频率、采样时间、数据点数、传感器数量和模型误差等因素对损伤识别结果的影响进行详细分析。
图3为10自由度剪切型结构[26],其参数如表1所示。第10层水平施加了均值为0、标准差为1、幅值为200 N的随机激励,3个加速度计分别安装在1层、5层、9层采集水平方向的加速度响应,采样总时间为1 800 s,采样频率为200 Hz,可计算得到组合相关函数R=[R1,5,R1,9,R5,9],选择R1,5,R1,9,R5,9的前100个数据点,共300个数据点用于损伤识别。假定单元3和单元8分别发生30%和20%的刚度损伤,即α3=0.3,α8=0.2。

表1 10自由度结构参数
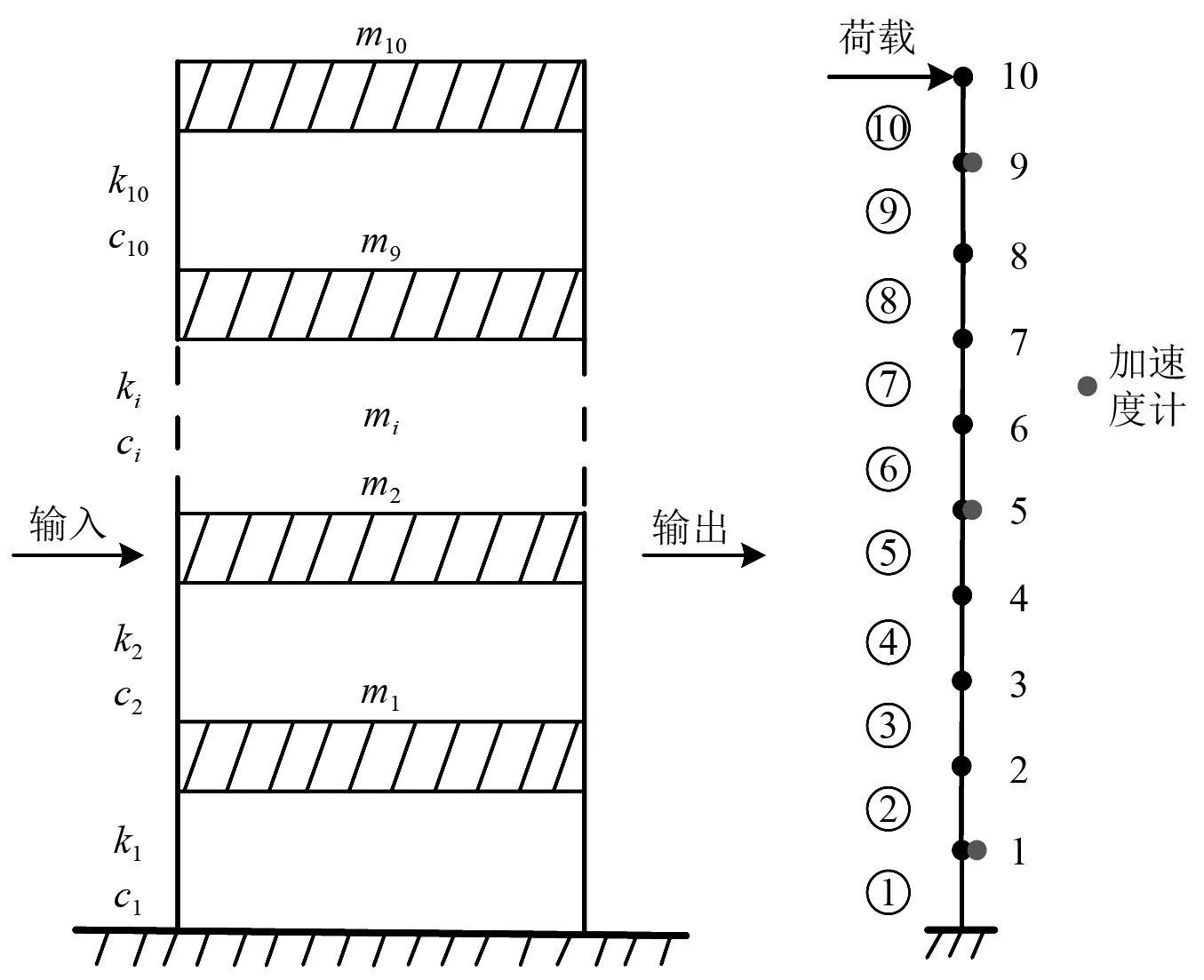
图3 10自由度结构模型
4.1 识别方法的有效性
采用遗传算法(genetic algorithm, GA)、Jaya和I-Jaya三种算法对比分析I-Jaya算法的性能,GA[27]的参数设置:种群规模为100,最大迭代次数为100,变异概率为0.2,交叉概率为0.8; Jaya算法的参数设置:种群规模为100,最大迭代次数为100;I-Jaya算法的参数设置:种群规模为60,最大迭代次数为50。为保证计算结果的准确性,各工况下优化算法分别计算5次,并取平均值作为最终的识别结果。
图4和表2分别为GA,Jaya,I-Jaya三种算法的目标函数收敛曲线和计算时间。可以明显观察到I-Jaya算法取得最优的计算效率,GA的优化能力最差,达到最大迭代次数100时目标函数值仍然小于200,GA,Jaya和I-Jaya三种算法的最终目标函数值分别为190.29,468.45,677.75。此外,由表2可知,GA,Jaya和I-Jaya的总评价次数分别为10 000,10 000和3 000。I-Jaya算法总计算时间为260.8 s,明显低于GA和Jaya算法所需的853.2 s和936.4 s。以上结果表明,与GA和Jaya相比,I-Jaya算法能够以最少的计算成本获得最优的计算结果。
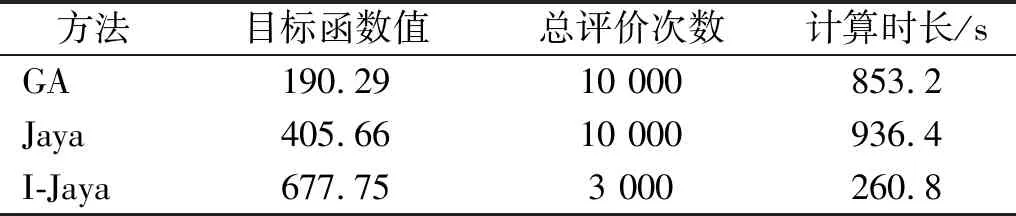
表2 三种算法的计算时间
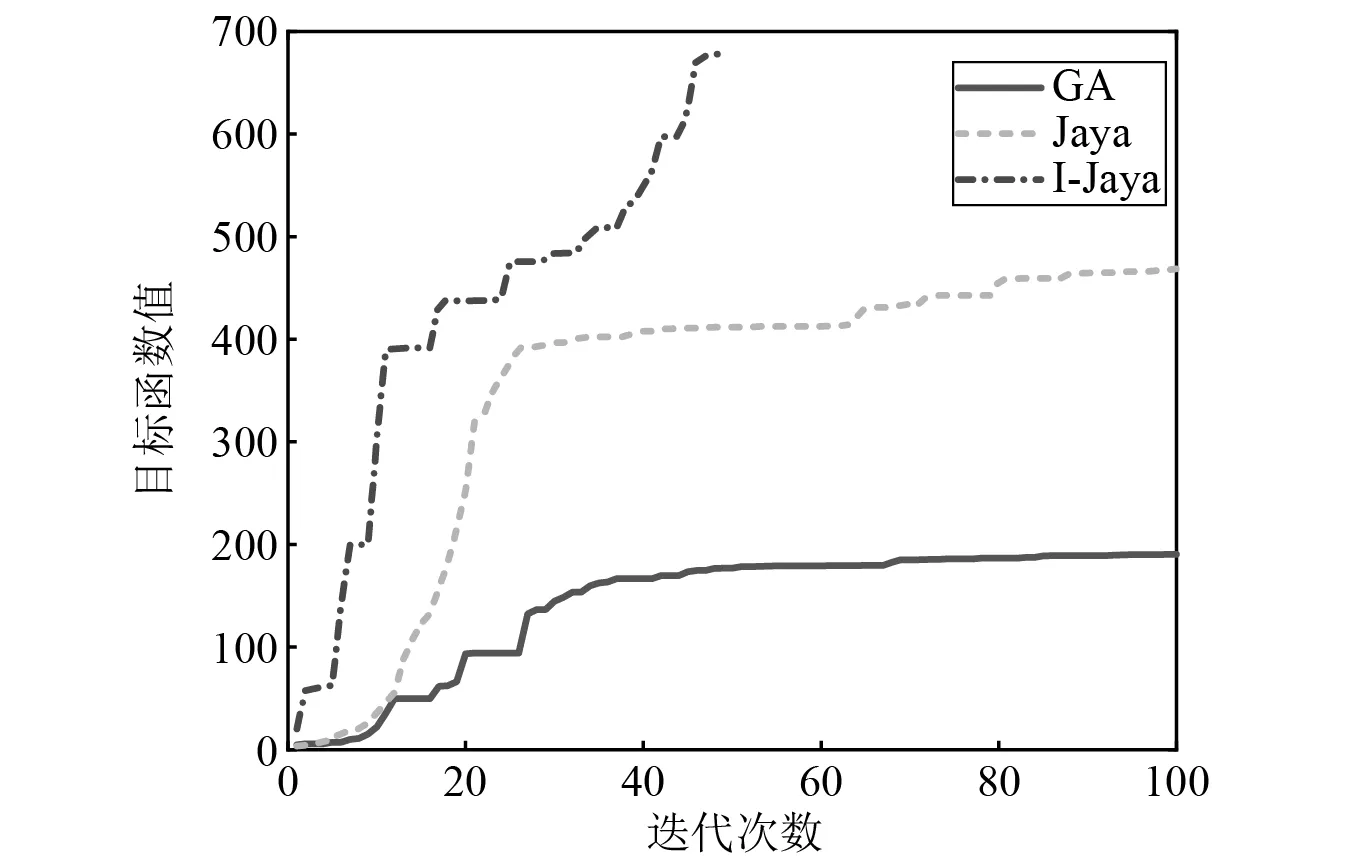
图4 目标函数迭代收敛图
无噪声时基于GA,Jaya和I-Jaya算法的10自由度结构的损伤识别结果,如图5所示。由图5可以发现,GA算法虽然能够识别损伤单元位置,但单元4、单元5、单元9存在明显的错误识别;Jaya算法能够成功识别损伤单元的位置,但不能准确识别单元3和单元8的损伤程度,最大和平均识别误差分别为2.55%和0.98%;I-Jaya算法既可以成功定位损伤单元的位置,又可以准确识别出单元损伤程度,且几乎没有错误识别,最大识别误差仅为1.88%,这表明基于I-Jaya算法和组合相关函数的损伤识别方法能够准确且高效识别结构损伤。
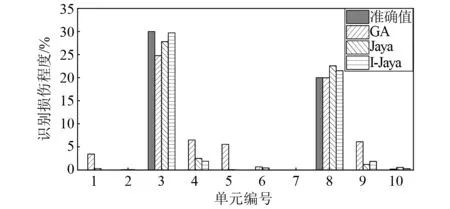
图5 10自由度结构损伤识别结果(无噪声)
为测试本文提出的损伤识别方法的鲁棒性,下面进一步研究其他因素对识别结果的影响。
4.2 噪声等级的影响
(23)
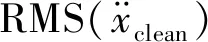
考虑10%,20%,30%三种噪声等级,使用I-Jaya算法的损伤识别结果如图6所示。由图6可以发现,随着噪声等级增加,识别误差逐渐增大,10%,20%,30%噪声时平均误差分别为0.77%,0.95%和1.01%,最大误差分别为2.94%,3.14%和4.94%。但即使在30%噪声等级下,最大识别误差不超过5%,这表明本文提出的组合相关函数具有良好的噪声鲁棒性。
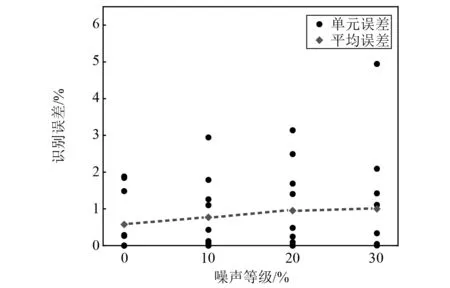
图6 不同噪声下的损伤识别结果
下面进一步分析组合相关函数对噪声不敏感的原因,0和20%噪声时互相关函数R5,9的对比结果,如图7所示。由图7可以发现,有无噪声时两者几乎重合,利用相对误差(relative error,RE)和皮尔森相关系数(Pearson correlation coefficient,PCC)量化
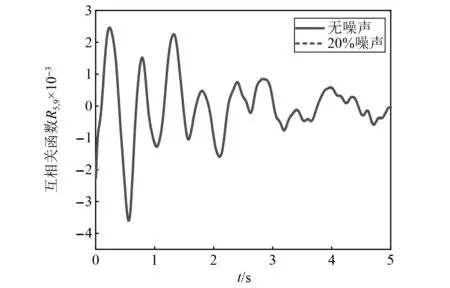
图7 0和20%噪声时R5,9对比图
(24)
(25)
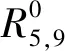
式(24)和式(25)计算结果分别为RE=1.47%,PCC=0.998 9,含有0和20%噪声时R5,9变化很小,这表明基于组合相关函数的方法对噪声不敏感。
4.3 采样频率的影响
10自由度结构的前10阶固有频率分别为0.76 Hz,1.98 Hz,3.29 Hz,4.47 Hz,5.63 Hz,6.59 Hz,7.43 Hz,7.98 Hz,8.75 Hz,9.25 Hz。采用5 Hz,10 Hz,20 Hz,50 Hz,100 Hz,200 Hz共六种不同的采样频率来研究其对识别结果的影响。不同采样频率下的识别误差,如图8所示。由图8可以发现,随着采样频率的增大,平均识别误差逐渐减小。当采样频率为5 Hz和10 Hz时,最大识别误差超过6%;而当采样频率大于20 Hz时得到较小识别误差。以上结果表明,较低的采样频率难以得到高阶模态的响应信息,不利于准确识别结构的局部损伤,因此结构振动测试前应根据结构固有频率合理选择采样频率。
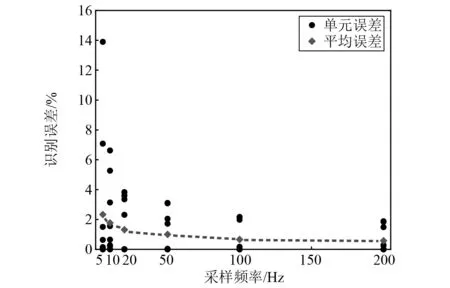
图8 不同采样频率下的识别误差
4.4 采样时间的影响
计算加速度响应的组合相关函数需要较长采样时间,共考虑5 min,10 min,20 min,30 min,40 min,60 min六种采样时间,研究其对识别结果的影响。 不同采样时间下的识别误差,如图9所示。由图9可以发现,随着采样时间的增加,识别误差逐渐减小。当采样时间不超过20 min时,最大识别误差超过6%,而采样时间大于30 min后识别误差变化不明显,但由表3可知,随着采样时间增加计算时间也明显增加,这表明盲目增加采样时间不能进一步提高识别精度,却消耗了更多计算时间。因此,在可接受的误差范围内,为节省计算成本,应合理选择采样时间。
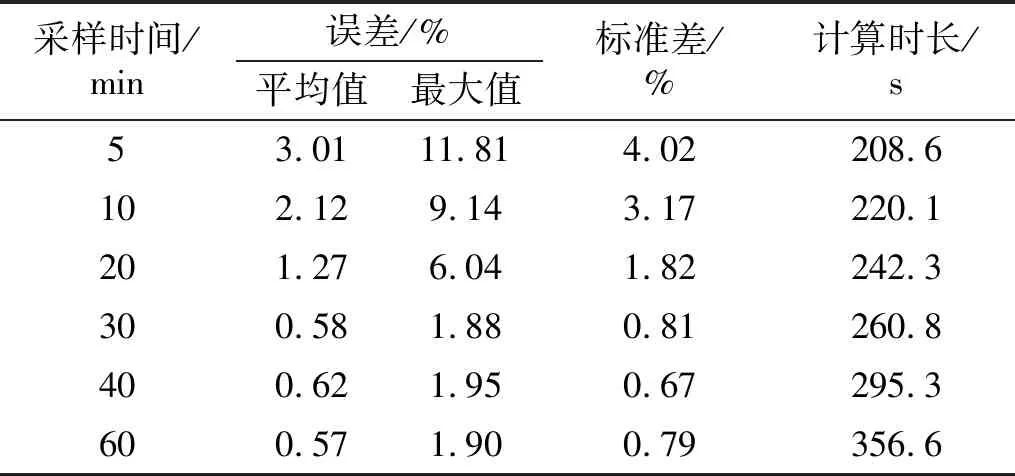
表3 不同采样时间下的识别结果
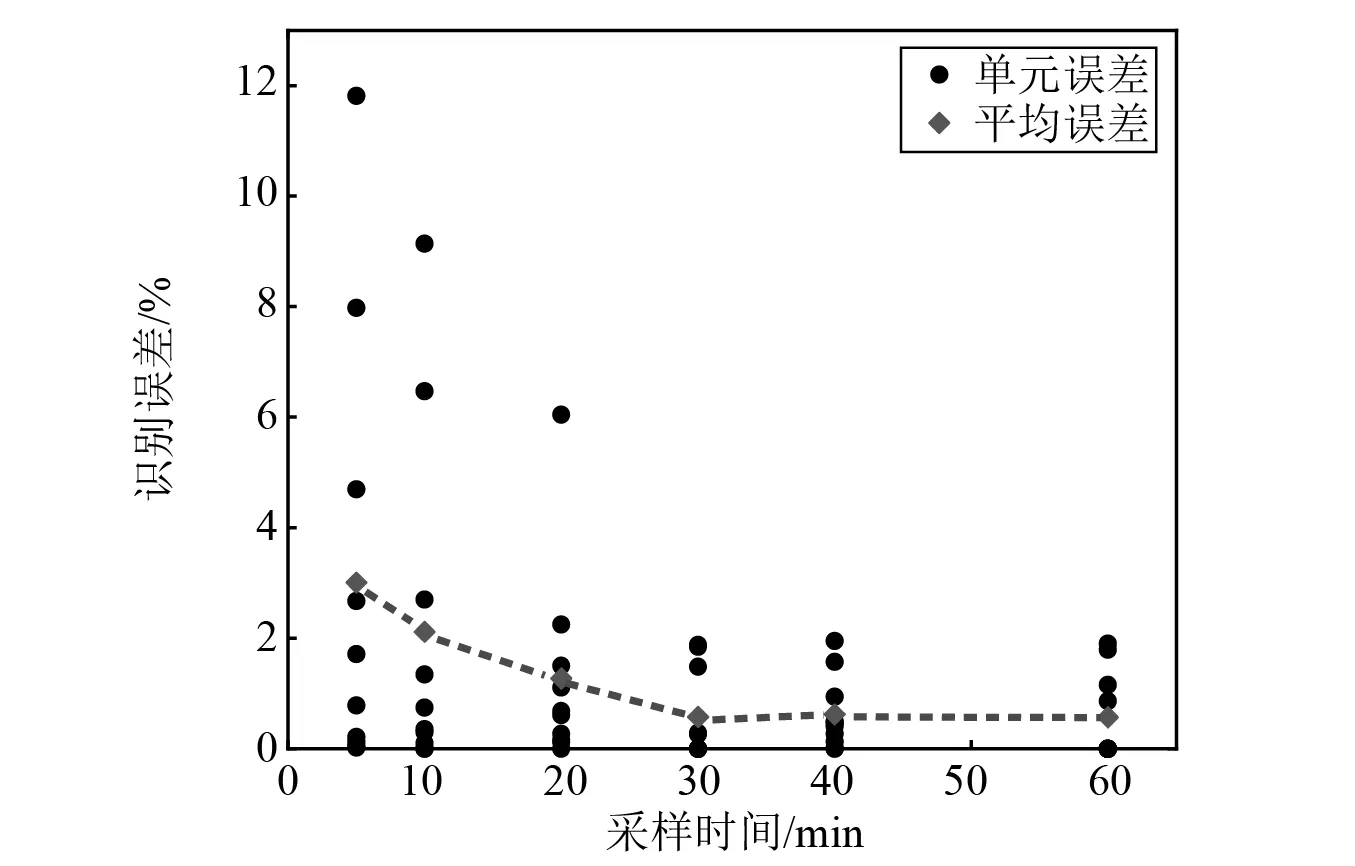
图9 不同采样时间下的识别误差
4.5 数据点数的影响
利用组合相关函数R=[R1,5,R1,9,R5,9]识别结构损伤时,需要确定互相关函数的数据点数量,考虑50,100,150,200,250,300共六种数据点数研究其对计算效率和识别精度的影响,结果如图10和表4所示。对比数据点数为100和300时,最大识别误差分别为1.88%和5.44%,计算时间分别为260.8 s 和776.7 s。可以发现,采用更多的数据点数没有提高结果的准确性,反而消耗更多的计算资源。为进一步研究该异常现象的原因,统计测量组合相关函数Rmea与估计组合相关函数Rest之间的相对误差,如表5所示,测量值与估计值的相对误差随着数据点数的增加逐渐累积,不利于识别结果的准确性。因此,综合考虑计算效率和识别精度,有必要合理选择数据点数量。
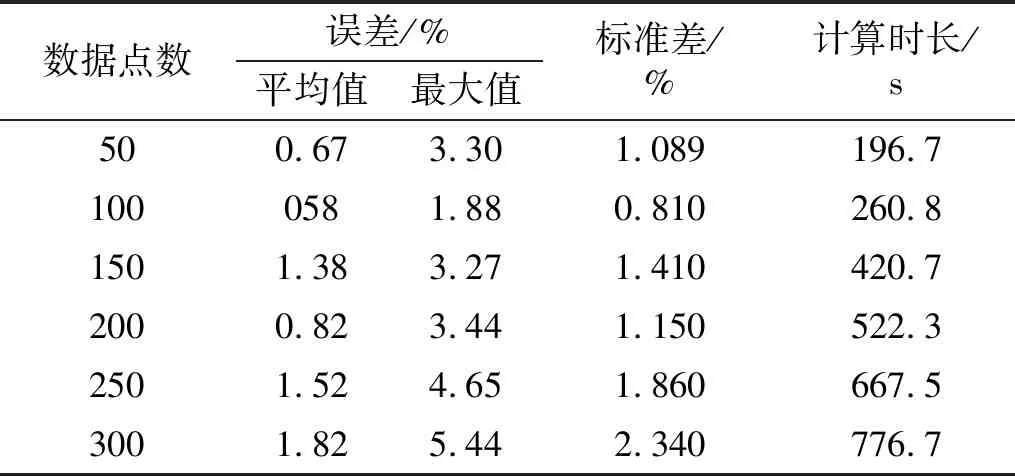
表4 不同数据点数时的识别结果
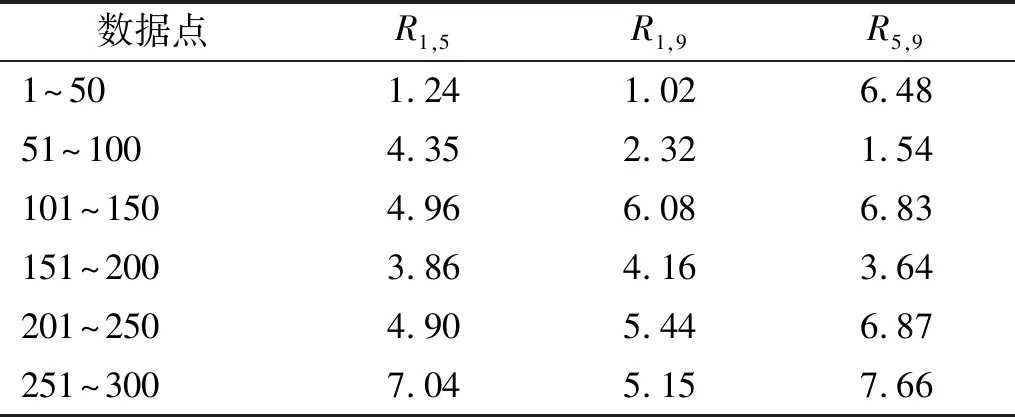
表5 互相关函数的相对误差
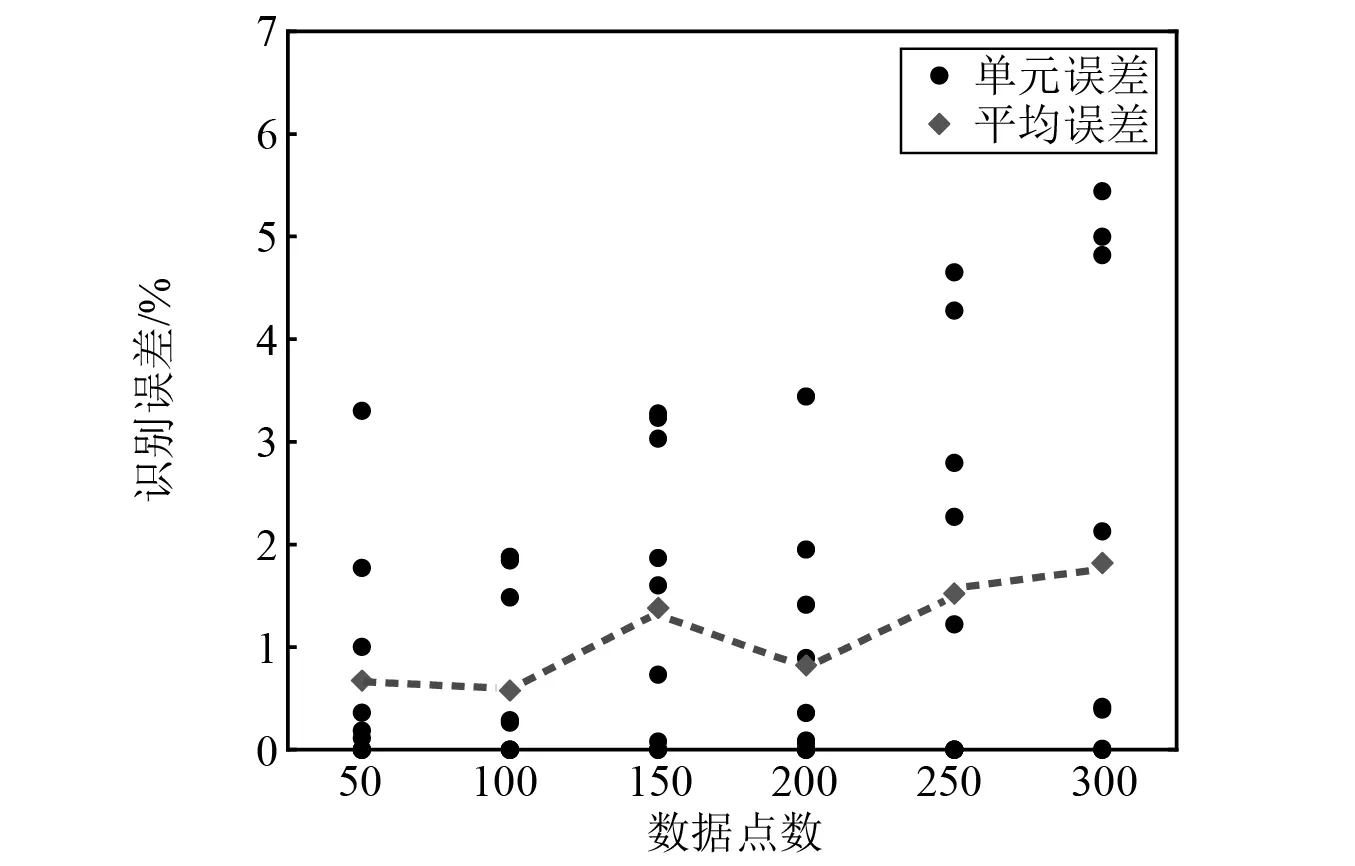
图10 不同数据点数时识别误差
4.6 传感器数量的影响
为研究传感器数量对识别结果的影响,考虑2,3,4,5共四种不同的传感器布置方案。2个传感器布置在4层、7层,得到组合相关函数R=[R4,7];3个传感器布置在1层、5层、9层,得到组合相关函数R=[R1,5,R1,9,R5,9];4个传感器布置在1层、3层、6层、9层,得到组合相关函数R=[R1,3,R1,6,R1,9,R3,6,R3,9,R6,9];5个传感器布置在1层、3层、5层、7层、9层,得到组合相关函数R=[R1,3,R1,5,R1,7,R1,9,R3,5,R3,7,R3,9,R5,7,R5,9,R7,9]。图11和表6分别为采用不同传感器布置方案时的识别误差和计算时间,可以明显观察到,平均识别误差随着传感器数目的增加而减小,采用3个以上的传感器时平均误差略有下降,但计算时间却明显增加。对比采用3个和5个传感器的识别结果,平均误差分别为0.58%和0.34%,计算时间分别为260.8 s和670.4 s。以上结果表明,盲目增加传感器数量并不能显著提高识别精度,反而增加了大量计算时间。 因此,在可接受的误差范围内,为节省计算资源,应合理选择传感器数量。
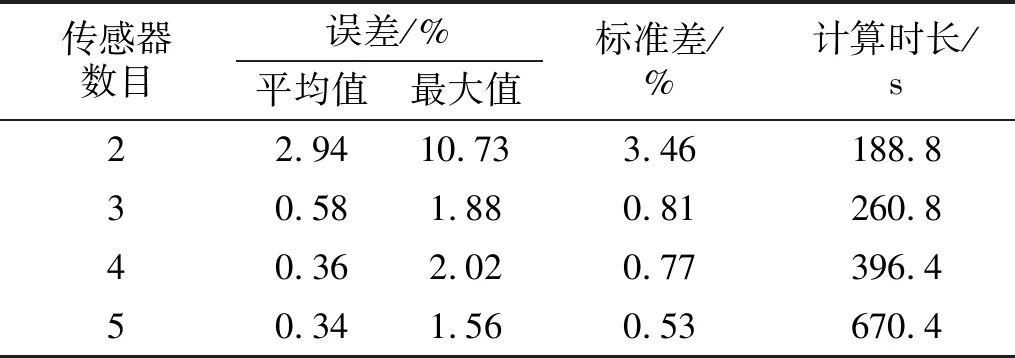
表6 不同传感器数量下的识别结果
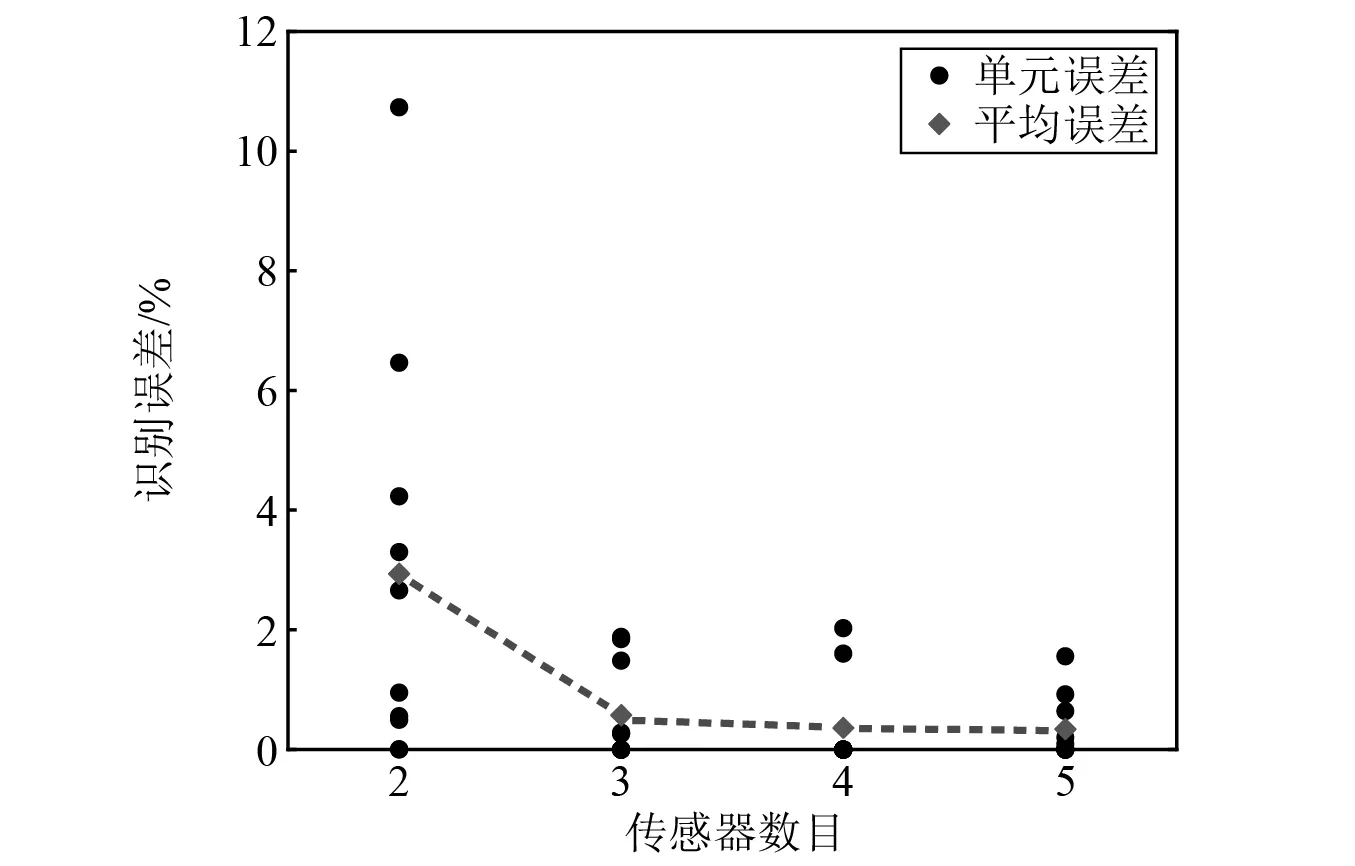
图11 不同传感器数量时的识别误差
4.7 模型误差的影响
本文提出的损伤识别方法需要不断修正有限元模型,结构模型的准确性将影响识别结果,因此,有必要考虑模型误差的影响。在[-1, 1]生成随机数乘以模型误差和结构参数值,引入0,5%,10%,15%和20%共五种模型误差考虑其对识别结果的影响,将含有模型误差的结构参数当作与识别参数比较的准确值,识别结果如图12所示。模型误差为0,5%,10%,15%和20%时,平均误差分别为0.58%,2.32%,5.75%和7.62%,10.96%,最大误差分别为1.88%,4.97%,11.21%,16.69%,18.93%,可以发现,模型误差显著影响了识别结果的准确性。因此,有必要通过划分更多单元、采用高阶单元类型和更精确的材料性质、边界条件等方法建立结构的有限元模型,而且损伤识别前应利用模型修正技术减小模型与实际结构的差异。
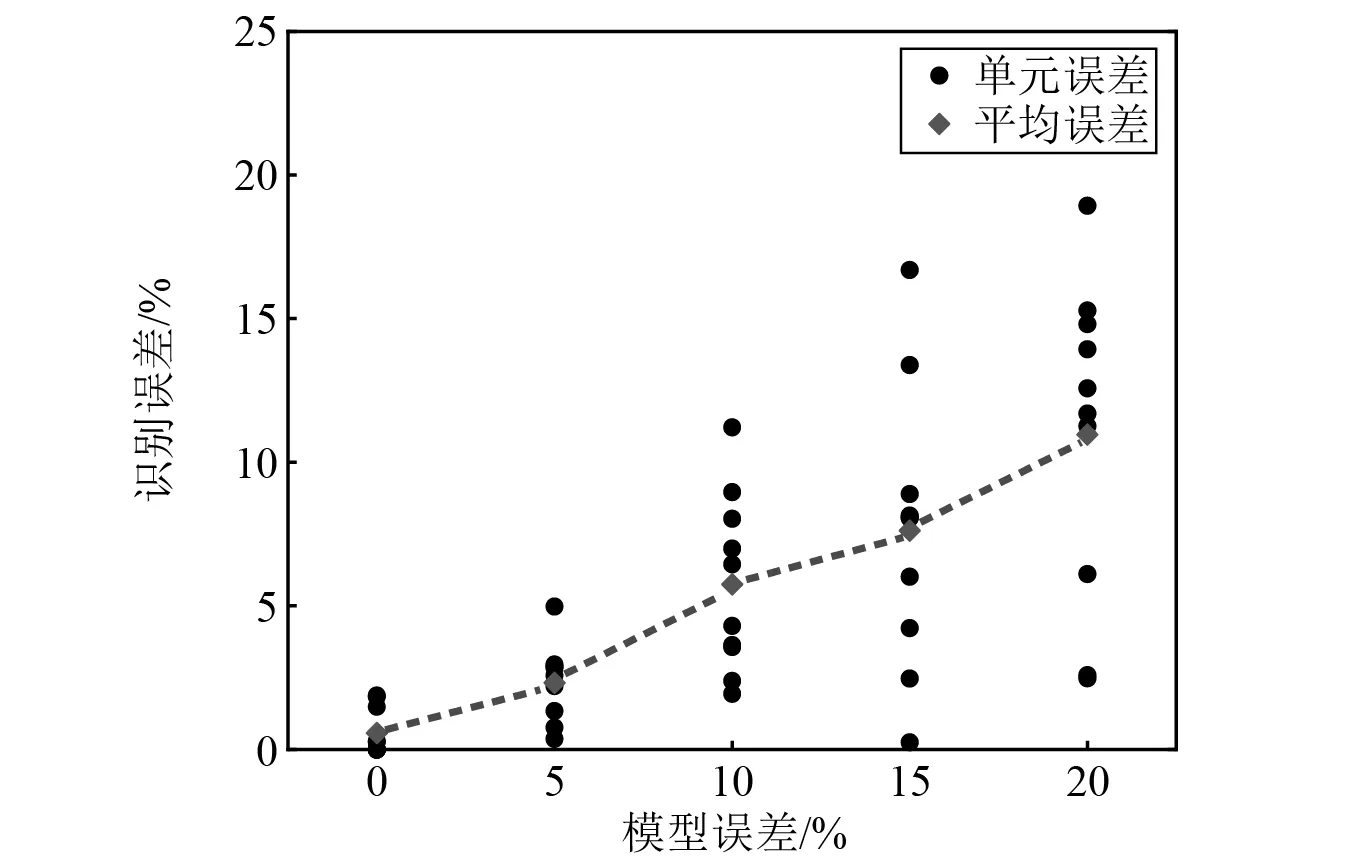
图12 不同模型误差下的识别误差
5 结 论
本文提出基于I-Jaya算法和组合相关函数的结构损伤识别方法,通过10自由度结构验证了该识别方法的有效性,并对优化算法、噪声等级、采样频率、采样时间、数据点数、传感器数量和模型误差等因素对识别结果的影响进行了分析,得出以下结论:
(1)引入Hammersley序列初始化、Lévy飞行搜索、经验学习策略三种改进机制,得到I-Jaya算法,该算法无需设置任何特定于算法的参数,结构清晰,操作简单。与GA和Jaya算法相比,I-Jaya算法可以更好实现全局搜索和局部搜索间的平衡,并在识别精度、计算效率等方面取得更优的性能。
(2)本文提出的组合相关函数无需定义参考点,且具有良好的噪声鲁棒性,即使在20%的噪声污染下,基于I-Jaya算法和组合相关函数的结构损伤识别方法仍能准确识别结构损伤的位置和程度。
(3)较低的采样频率不利于准确识别结构的局部损伤,结构振动测试前应根据结构固有频率合理选择采样频率。模型误差会降低识别结果的准确性,结构损伤识别前应利用模型修正技术得到与实际结构更加一致的有限元模型。
(4)盲目增加采样时间、数据点数、传感器数量将消耗更多的计算成本,但不能显著提高识别精度,甚至识别误差随着数据点数增加而累积。综合考虑计算效率和识别精度,应合理选择采样时间、数据点数和传感器数量。
