动车传动系统的振动特征分析
2023-10-31杨绍普梁儒全杨月婷
杨 柳, 杨绍普, 梁儒全, 杨月婷
(1.临沂大学 机械与车辆工程学院,山东 临沂 276000;2.石家庄铁道大学 机械工程学院,石家庄 050043)
近几年,由于动车关键部件健康管理技术的需求,制造商及其研究院校更加关注动车关键部件的振动机理及其故障演变规律,如何能够准确的表征关键部件振动响应特征成为研究重点。因此,建立完备的动车传动系统动力模型,模拟动车的实际运行状态,研究传动系统的关键部件的振动特征。完备的动力学模型不仅能够节约研究成本且能够为系统关键部件故障诊断及运行维修提供理论指导。
国内外学者,建立了整车动力学模型,研究了整车运行平稳性、轮轨接触影响及车体振动特性的影响。Zhai等[1]提出了车辆-轨道耦合动力学模型,研究了车辆-轨道垂向和横向响应功率谱特征,分析了轨道对车辆振动的影响。Chen等[2]基于车辆轨道耦合动力学模型,将齿轮传动引入模型中,研究了不同工况下动车齿轮箱的振动特征。徐宁[3]建立了考虑电机-联轴器-齿轮箱的车辆模型,并分析了车体振动传动规律和响应特性。Wang等[4]针对城市列车纵向垂向振动异响问题,引入变位齿轮模型,分析了齿轮裂纹、剥落等时域响应振动特征。黄冠华等[5]利用仿真软件建立动车模型,研究了在轮轨激励影响下齿轮箱箱体的振动特征。Shenani等[6]利用有限元软件,建立了柔性车体模型,研究了轮轨接触力对构建的影响。孙刚[7]建立了动车传动系统有限元模型,研究了车辆构架及其电机的振动响应特征。Anders等[8]分析了列车实测数据下轮轨接触应力,并通过钢轨塑性累加时域特征计算出了轮轨磨耗周期。金学松等[9]考虑轮轨接触特征,给出了轮轨磨耗及形成机理。Wang等[10]基于CHR380刚性整车模型,考虑轴承-齿轮等关键部件,研究了不同载荷及轮对变形下轴承振动特性。查浩等[11]建立轴箱轴承动力学模型,分析轮轨激励变化对轴承振动寿命影响。Zhang等[12]改进了轨道车辆耦合动力学模型,研究了不同转速下对系统振动的响应特征。Chen等[13]基于车辆耦合动力学模型,分析车辆启停对车辆关键部件的影响。
考虑上述问题,本文针对动车服役时不仅承受轮轨接触力、电机不平衡力等外部激励的作用,同时也需承受轴承-齿轮内部接触产生的激励,建立动车传动系统刚柔耦合动力学模型,能够更好的研究传动系统关键部件的振动响应特征。比较不同工况下传动系统关键部件的主要振动响应特征,掌握系统振动规律,为后续开展动车关键部件的疲劳测试及振动分析提供理论基础。
1 刚柔耦合动力学模型
受随机轮轨激扰力,动车传动系统为高维强非线性复杂系统。为研究动车关键零部件的振动特征,本文考虑轮轨接触、轴承接触变形及轴承、齿轮啮合、构架的影响,建立了动车传动刚柔耦合多体系统动力学模型,如图1所示。动车传动系统模型主要包括构架、电机、轮对、齿轮箱、轴承及悬挂弹,其中,电机与构架相连接,动力由齿轮箱传递给轮对,轮轨踏面接触实现车辆移动,轮对轴箱轴承内圈与轮对相连,轴箱通过减振弹簧与构架相连,建立模型中轮对为柔性体,其他为刚性体。

图1 传动系统模型图
1.1 柔性轮对转子模型
基于有限元法网格划分轮对轴,每个单元节点的柔性坐标为Rf(x,y,z,t)=(ui,vi,wi,φi,φi,θi) 。系统动力学简图如图2所示,考虑横向弯曲和扭转变形,轮对质心刚体运动坐标Rr=(X,Y,Z),柔性轮对转轴任意节点位移表达式为
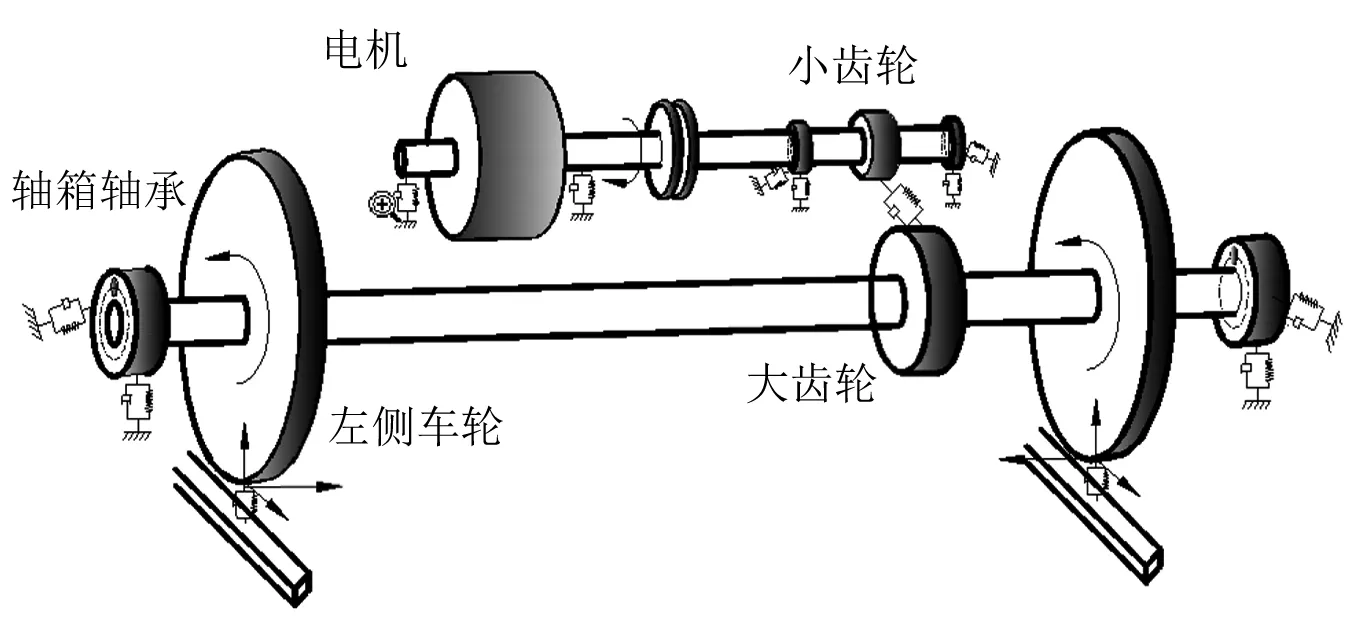
图2 传动系统动力学简图
R=Rr+Rf
(1)
任意节点速度
(2)
轮对绕轴旋转转速
V=Ω×Rr=(0,ΩZ,-ΩY)
(3)
将式(2)、式(3)代入式(1)中得
(4)
轮对动能表达式
(5)
式中:ρ为密度;A为单元横截面积;Ω为转速;IO为极转动惯量;Id为转动惯量。
模型中考虑轴向、扭转、剪切和弯曲变形而产生的应变势能为
(6)
式中:μ为剪切因子;E,G分别为转子材料的弹性模量、剪切模量。
将式(1)、式(4)、式(5)和式(6)代入拉格朗日方程
(7)
式中,Qi为外力,轮对柔性任意节点处系统动力学方程为
(8)
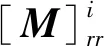
1.2 齿轮啮合单元模型
高速动车齿轮箱齿轮单元动力学模型如图3所示。主动轮与从动齿轮节点处坐标为{q}c=(uci,vci,wcj,θix,θiy,θiz,ucj,vcj,wcj,θjx,θjy,θjz),其中,kc(t)为齿轮时变啮合刚度[14],c(t)齿轮啮合的综合阻尼系数;mi,mj为主从动齿轮质量;Ti,Tj分别为输入、输出转矩;ei,ej为主从齿轮偏心距;βij为螺旋角;ψij为法向压力角。
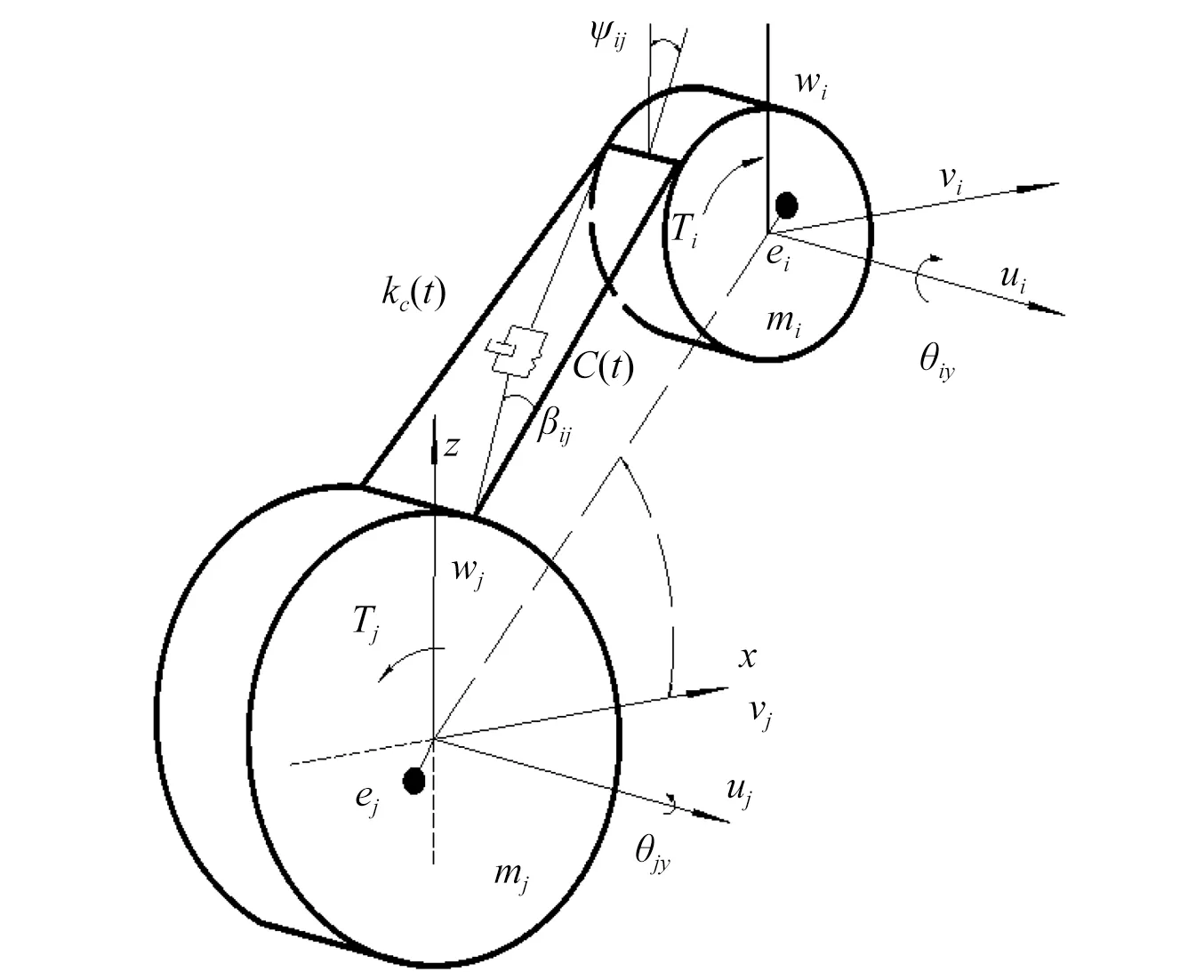
图3 斜齿轮啮合单元模型
假设齿轮啮合时,齿轮基体不变形及齿轮啮合端面弹性变形,主动轮齿轮的动力学方程为
(9)
从动轮齿轮的动力学方程为
(10)
式中,d(t)=sgn(uci-wci)sinψij+(vci-vcj)cosψij+sgn(uci-ucj)+riθxisinψij+rjθzjcosψij-riθyjcosψij,sgn为符号函数,将式(9)、式(10)整理为
(11)
式中,[M]c,[C]c,[G]c和[K]c分别为齿轮质量矩阵,阻尼矩阵,陀螺项和时变刚度矩阵,其中斜齿轮啮合节点时变啮合刚度[K]c的表达形式为
(12)
其中
Aij=[-sinβij,sinψijcosβij,cosψijcosβij,sgnricosβij, sgnrisinψijsinβij,sgnricosψijsinβij;
sinβij,-sinψijcosβij,-cosψijcosβij,sgnricosβij,
sgnrisinψijsinβij,sgnricosψijsinβij;]
式中,ri和rj分别为主、从动齿轮的半径。
齿轮啮合点荷载力为
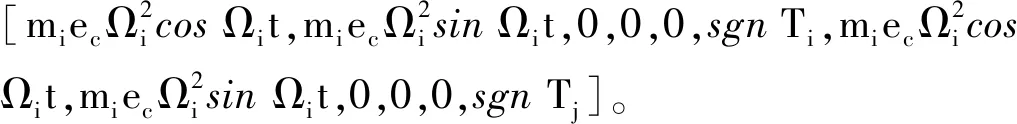
1.3 圆锥滚子轴承节点
考虑轴承轴向作用力及法向接触力的影响,高速动车轴承轴箱圆锥滚子轴承动力学模型如图4所示,由非线性赫兹接触理论,可得滚动体与滚道所产生的荷载力
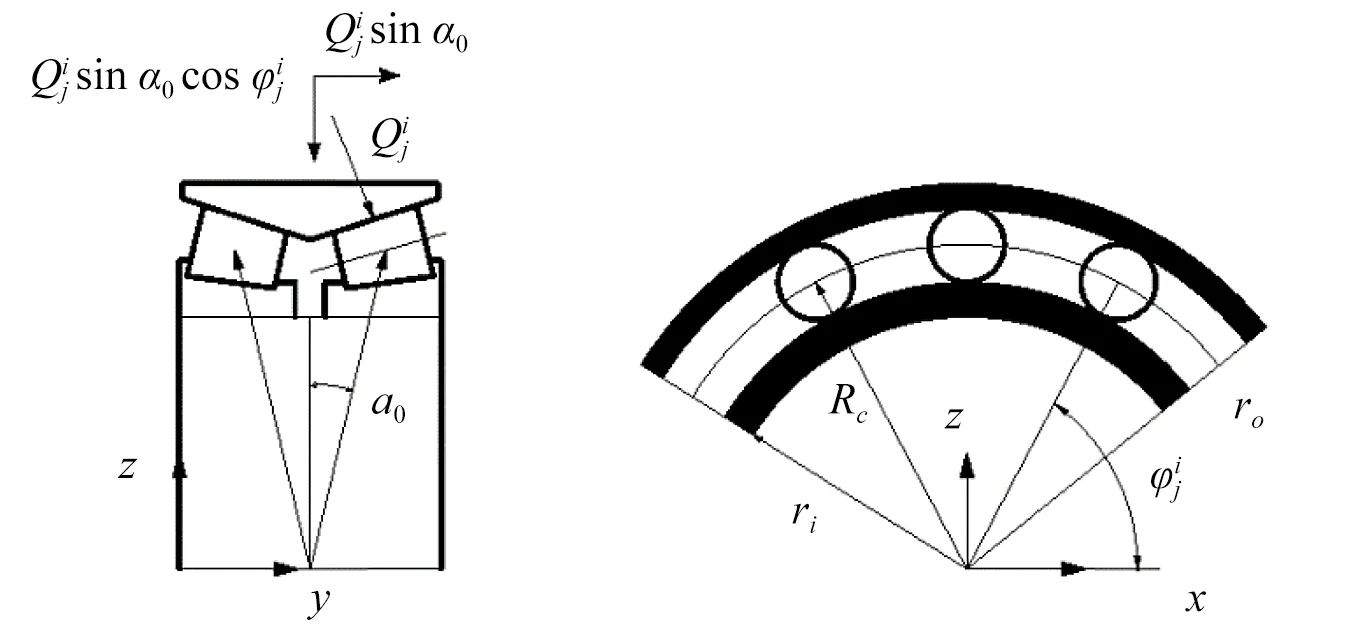
图4 轴承接触单元模型
(13)
(14)
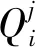
轴承第j个滚子接触载荷力为
(15)
式中:Kbe为轴承内、外圈表面接触刚度,其表达式为
式中,Ki,Ko为内、外圈刚度。Δ为轴承径向变形量,其表达式为
(16)
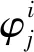
轴承节点的动力学方程为
(17)
式中,[M]b,[C]b,[K]b和[F]b分别为轴承质量矩阵,阻尼矩阵、支撑刚度和接触作用力。
1.4 车轮节点动力学模型
轮轨结构示意模型如图5所示,轮轨接触力为FN及蠕滑力为Fl,车轮节点坐标为(uli,vli,wli,φli,φli,θli,i=1,2),考虑到滚接触引起的变形,利用拉格朗日方法,车轮节点动力学方程为
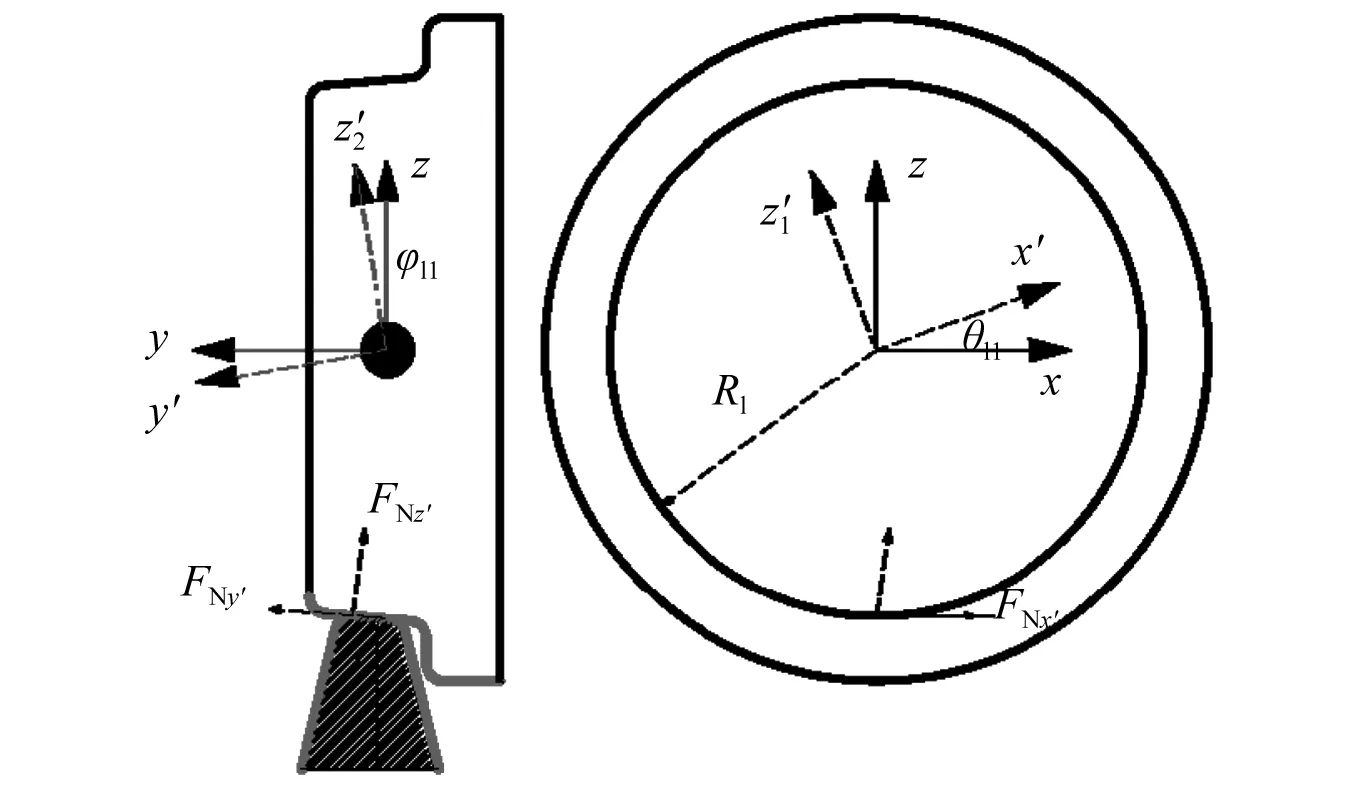
图5 车轮钢轨接触单元模型
(18)
式中,[M]l,[C]l,[G]l和[K]l分别为轮对质量矩阵、阻尼矩阵、陀螺项和支撑刚度矩阵。
车轮中心初始参考坐标为{x,y,z},车轮节点变形之后的坐标为
(19)
式中:φli为车轮侧滚;φli为车轮摇头。
车轮轮毂为刚性体,主要考虑轮轨接触型面特征,轮轨接触踏面如图6所示。将轮轨接触表面进行切片,初始状态下车轮与轨道任意接触节点的坐标为
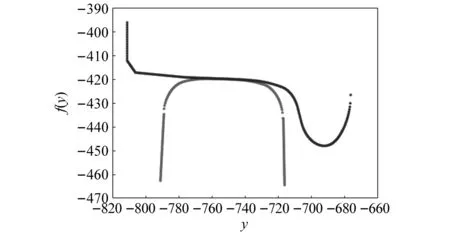
图6 轮轨接触型面
(20)
式中,下标im,is分为车轮沿x和y方向分割数中任意坐标,代入式(19),可得变形后接触点坐标。
沿车轮y方向,轮轨任意接触点的垂向距离表示为
(21)
柔性轮对则不能采用迹线法求取接触点位置,本文利用轮轨变形之后横向位移搜寻轮轨接触区域点,公式如下
(22)
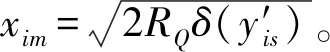
由Piotrowski[15]给出Non-Hertzian法向接触应力,计算公式为
(23)
式中:E和v分别为轮轨弹性模量和泊松比;D为接触区域;δ为变形量。考虑轮轨接触相对滑移,轮轨法向接触力为
(24)
式中,ε为黏着系数。
切向接触应力计算,对滑移单元面积积分得
F=∬slipτdxdy,Fx=fvxN′,Fy=fvyN′
(25)
式中,vx,vy分别为车轮节点纵向和横向滑动率。
1.5 系统整体动力学方程
基于拉格朗日法,考虑轴承、齿轮及轮对因素的影响,系统整体动力学方程为
(26)
式中:{q}=[u1,v1,w1,φ1,φ1,θ1,…θn]T,n为节点个数;[M],[C],[G],[K]和[Q]分别为系统整体质量矩阵、阻尼矩阵、陀螺项、刚度矩阵、载荷矩阵。
2 高速动车传动系统振动分析
高速动车CRH380型号为研究对象,模型主要参数如下:转向架质量mv=2.2 t,车轮质量ml=1.1 t,齿轮箱齿轮质量mc1=20 kg,mc2=120 kg,齿数为z1=14,z2=63齿宽系数Bg=80 mm。轴箱轴承NJ2232 型号,滚子个数NB=17,ri=160 mm和ro=210 mm分别为轴承内、外圈半径,主动轴运行转速n1=1 600 r/min。其他轮轴参数详见文献[16]。
2.1 系统幅频响应特征
考虑时变啮合刚度Km影响,系统前16阶固有频率值如图7所示。局部放大图7,1阶固有频率特征如图8所示,随齿轮时变啮合刚度的变化,系统固有频率值有明显的波动。齿轮刚度不变条件下,系统各阶固有频率如图9所示。
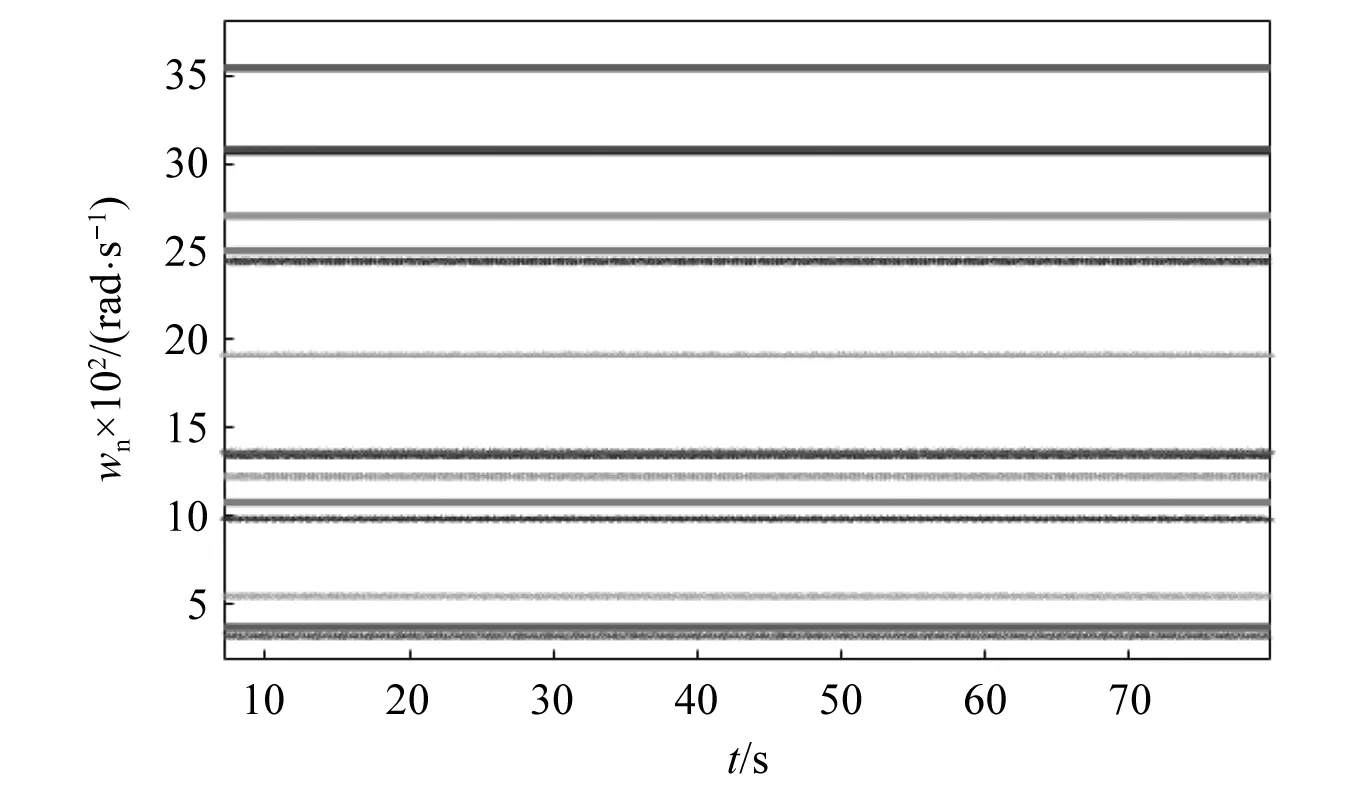
图7 系统固有频率
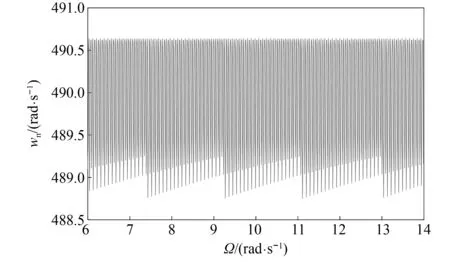
图8 固有频率局部图
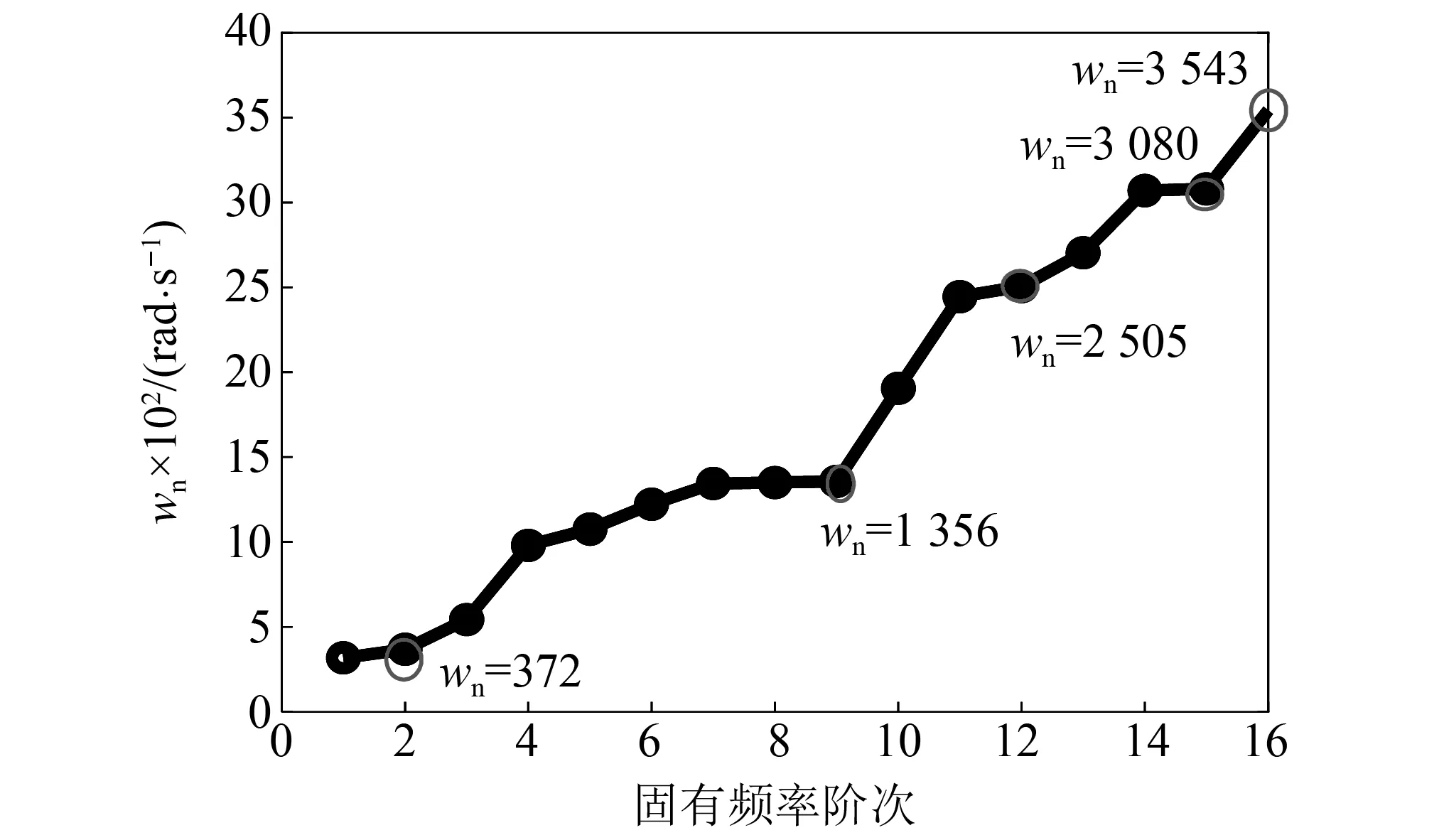
图9 各阶固有频率
系统振动幅频响应如图10所示,主轴角频率w=368 rad/s与第2阶固有频率值wn=372 rad/s近似相等时,系统出现共振现象。当主轴角速度w=3 079 rad/s与第15阶固有频率值wn=3 080 rad/s临近时,系统共振幅值最大。因此,动车启动、运行及停车时都应该越过临界角速度wn,避免引起系统振动幅值过大。
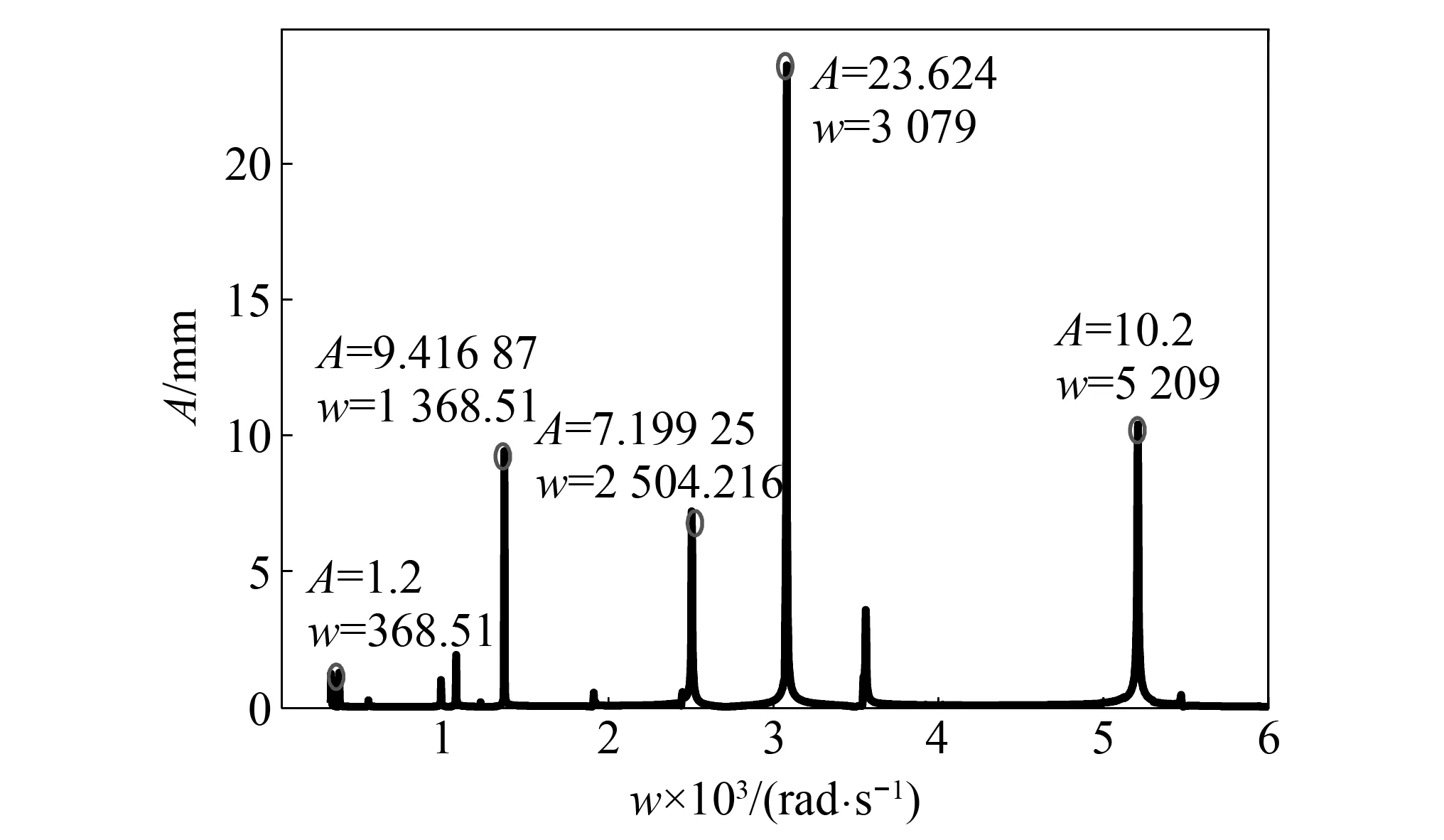
图10 系统幅频响应
2.2 不同工况下系统时域响应特征
动车前期运行时,无随机轮轨激励条件下,当转速w1=277 rad/s,w2=368 rad/s,w3=450 rad/s,w4=520 rad/s,w6=600 rad/s时,左侧轴箱轴承加速度时域响应如图11所示。主轴角速度w=368 rad/s时,加速度时域响应十分突出。轴承节点频域响应特征如图12所示,能够找到明显的齿轮啮合频率及其倍频特征,而系统固有频率处振动幅值并不明显。加速度响应的最大幅值如图13所示,当主轴角速度w=368 rad/s与wn=372 rad/s近似相等时,加速度响应幅值明显较大,但随着速度的增加,加速度幅值响应逐渐提高。
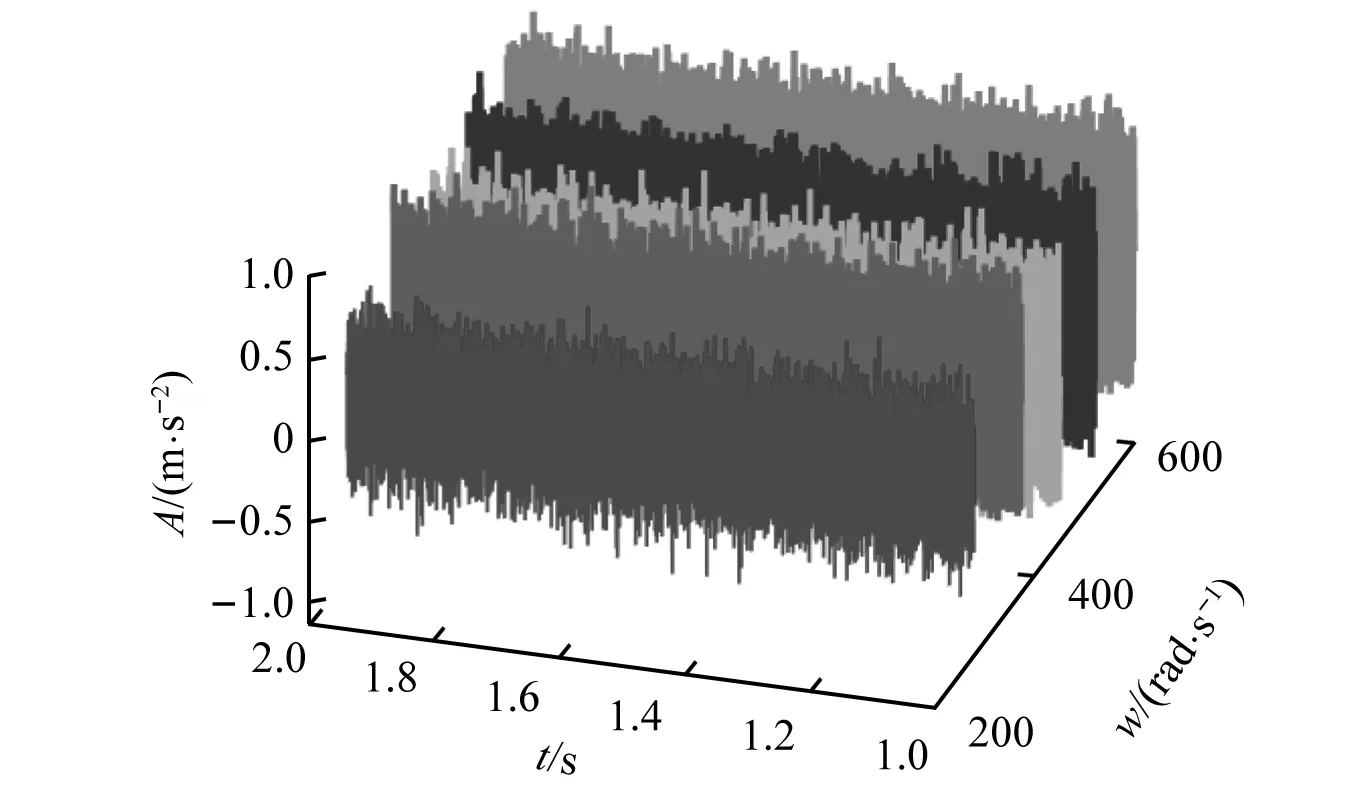
图11 左侧轴箱垂向振动时域响应
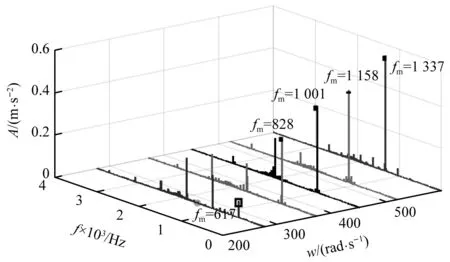
图12 频域响应
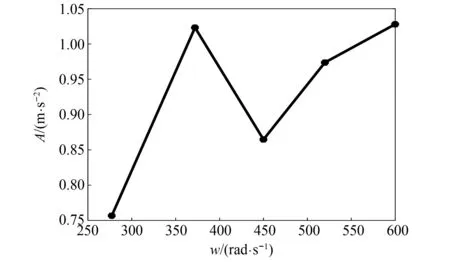
图13 加速度最大振动幅值
加载正常随机轮轨干扰激励及不同速度,左侧轴箱轴承垂向振动响应如图14所示。当主轴角速度w=368 rad/s接近固有频率wn=372 rad/s时,系统振动加速度响应峰值较大。轴承节点频域响应特征如图15所示,能够找到齿轮啮合频率及其倍频特征,随机轨道谱作用下,系统固有频率处频域响应明显。不同转速条件下,加速度响应的最大幅值如图16所示,主轴角速度w=368 rad/s与wn=372 rad/s邻近时,系统加速度振动响应较大。结论如下:无轮轨随机干扰时,轴承节点振动特征主要以齿轮啮合频率主。轮轨随机干扰较大时,轴承节点有明显的齿轮啮合频率及固有频率。
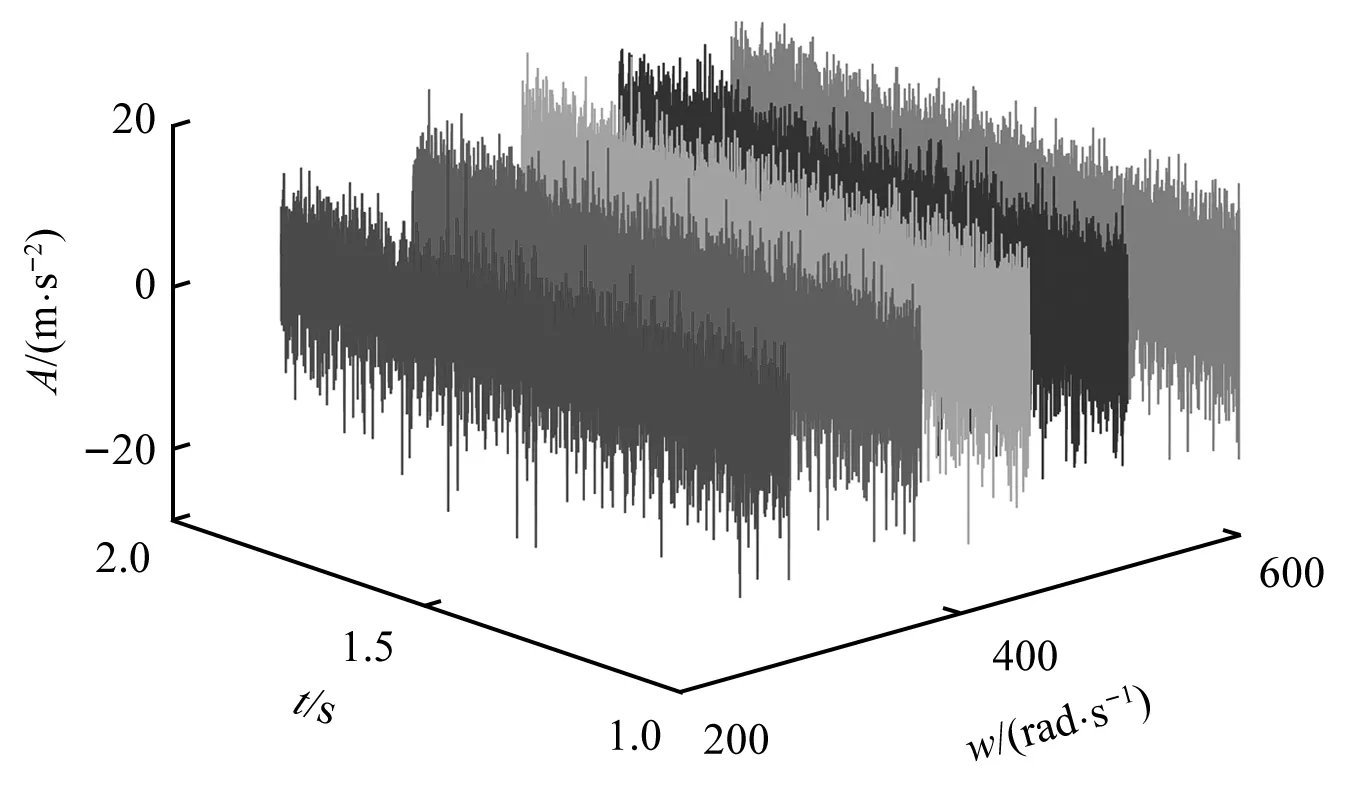
图14 左侧轴箱垂向振动时域响应
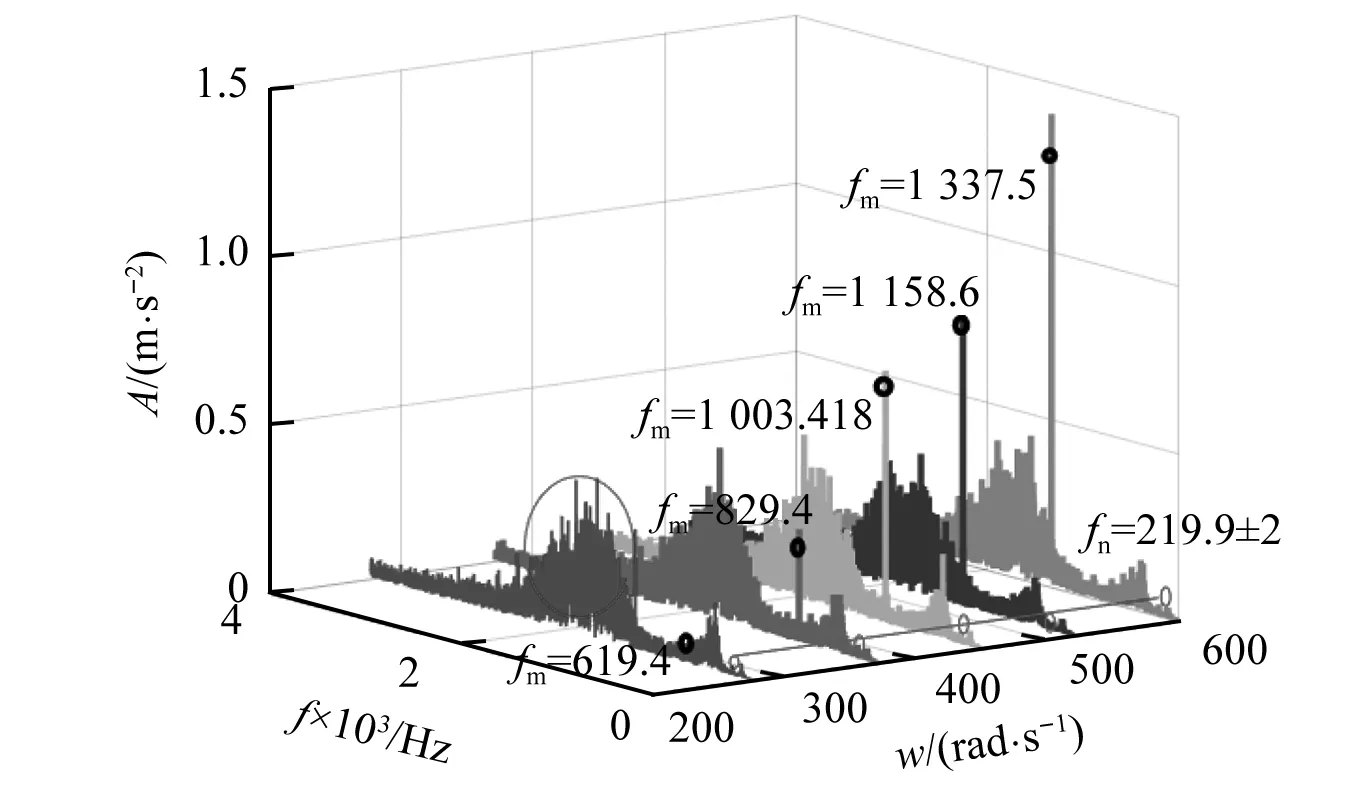
图15 频域响应
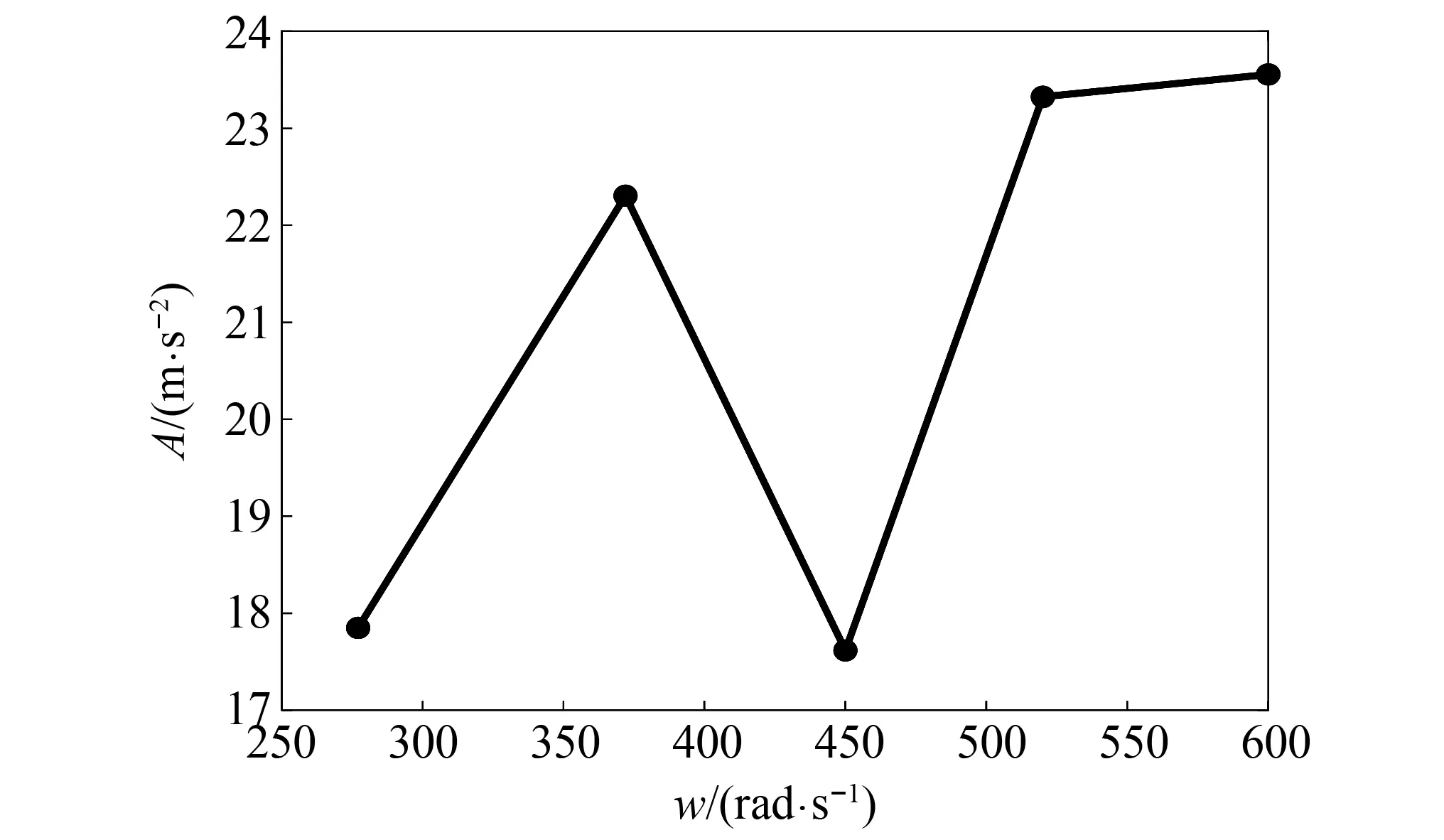
图16 加速度最大振动幅值
随机轮轨激励条件下,当主轴角速度w=600 rad/s时,齿轮节点与左侧车轮节点加速度垂向时域响应如图17所示,齿轮与车轮节点加速度振动幅值基本保持一致,车轮节点加速度幅值伴有轮轨冲击引起的脉冲。频域响应图中,齿轮节点频域特征主要有齿轮啮合频率及其倍频特征,具有转轴引起的边频特征;而车轮节点频域响应特征中仅有1阶啮合频率特征及随机轮轨干扰频率,系统固有频率特征并不明显。
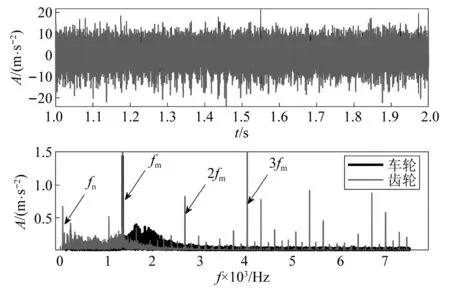
图17 车轮与齿轮节点加速度振动
为了验证高速动车传动系统动力学模型的准确性及可行性,采用标准动车组跟踪试验数据与动力学仿真数据进行对比,主要对比左侧轴箱轴承的垂向振动,加速度传感器具体安装位置如图18所示,采样频率f=12 800 Hz,动车运行速度V=100±5 km/h。

图18 加速度安装位置
动力学模型结果与实测标动跟踪数据的时域频域仿真对比如图19和图20。如图19所示,相同转速条件下,左侧轴箱仿真加速度时域响应均方根值RMS=6.804 7×10-5与试验采集的RMS=6.714 6×10-5基本保持一致,仿真与实测数据存在一定相位差,但总体的振动趋势基本一致相似。如图20所示,仿真数据与实测数据的频域对比,都存在明显的齿轮啮合频率特征fm=861.1 Hz及倍频特征2fm=1 722.17 Hz,且振幅大小上基本一致。其中,仿真与实测数据在固有频率fn=217.03 Hz及fn=1 690 Hz处的振动能量十分突出。

图19 左侧轴箱轴承垂向时域响应
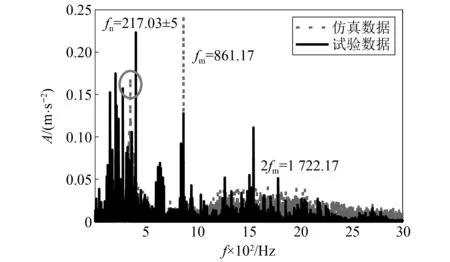
图20 频域响应
3 结 论
基于刚柔耦合动力学理论,考虑轴承-齿轮-轮对结构特征,建立了动车传动系统刚柔耦合动力学模型。求解了系统固有频率,探究了系统幅频响应特征,研究了不同工况下传动系统主要振动响应变化。总结论如下:
(1) 动车传动系统模型数据与实测数据对比结果基本一致,保证了模型的可靠性。
(2) 系统固有频率特征受齿轮啮合刚度的影响,具有时变特性。
(3) 无随机干扰下,系统振动主要以齿轮啮合频率为主,随机干扰下,轴承节点有明显的共振现象。齿轮节点振动主要以齿轮啮合频率与转轴边频特征,车轮节点处振动伴随有轮轨强干扰频率,节点频率有明显区别。
以上分析结果对研究动车传动系统关键部件故障的振动机理和演化规律具有一定的价值。
