含集中质量的斜置输流管路的流体诱发振动分析

刘 伟, 赵千里

(常州机电职业技术学院 机械工程学院,江苏 常州 213164)

随着人类在探索土地、深海、太空等领域的不断深入,对各类机械装备的性能也提出了越来越苛刻的要求,输流管路作为大部分整机系统不可或缺的组成部分,因其在制造材料以及截面形状等方面具有多样性,还因其便于生产制造、可通过组合构造任意空间构型等特点,输流管路被广泛应用于各种场合,如:空间站机械臂的液压系统,长距离石油、天然气的传输系统,城市的供热管网系统,中央空调的送风系统,农田灌溉用水泵的抽水、送水系统,化工行业液体原料的输送系统等。

正因如此广泛的应用范围,导致在正常服役期间,输流管路难免会因内部流体压力不均、流速过快、存在杂质、材料本身存在缺陷、外部存在激振源等因素而诱发管路系统发生机械振动。在近半个世纪以来,借助飞速发展的自然科学技术,学者们从多个方面对管路的流固耦合振动问题开展了研究逐渐形成了两大研究分支[1]：其一,建立问题的数学模型;其二,开发高效准确的数值方法。

目前,人们在建立研究输流管路流固耦合振动问题的数学模型时多以梁模型为理论基础,如:以Paidoussis教授为首的科研团队[2-7]基于Euler-Bernoulli梁模型,从支承、材料属性、空间构型、激励等方面出发建立了管路的振动微分方程,并提出了许多重要的理论,如:Paidoussis耦合模态颤振、关于弯管轴线是否可伸长的三大理论等。

在数值方法方面,在近半个世纪以来,随着计算机技术的不断进步,大量的数值方法也随之发展起来,在求解管路振动特性方面典型的方法主要包括:传递矩阵法[8],微分变换法[9],微分求积法[10]或其广义形式[11],格林函数法[12]等。

前面提到的所有研究结果的共同点在于:管路的放置方向为水平或竖直。考虑到在实际的工程应用中,倾斜安置的管路并不少见,如:草坪的喷洒灌溉系统、喷泉的供水系统等。此外,很多场合下管路上需要添加附加质量以控制系统的动力学表现,如:消防车的水炮、发电站冷却塔内的喷淋管路、含喷嘴的喷泉供水管路及含附加质量的城市洒水车的出水管路等,然而,同时研究这两个因素对管路振动特性的影响的报道却鲜有提及。

由于多数场合下管路两端的支承沿管路轴线方向具有一定的长度,可以近似视为固定-固定的支承形式,因此,本文重点研究在该支承形式下含集中质量的斜置输流管路的流体诱发振动特性。首先,以数学表达式表示了由倾斜角度和集中质量引起的管路受力的变化,而后将它们引入Euler-Bernoulli型输流直管基本的流体诱发振动微分方程,得到了系统的动力学偏微分方程;其次,基于作者提出的基于新型形函数的Galerkin法[13]对上述偏微分方程进行离散,经过推导,获得了计算系统固有频率的特征方程;最后,研究了倾角和集中质量对管路固有频率及临界流速的影响。

1 振动微分方程

含集中质量的斜置输流管路的力学模型如图1所示,其中管路总长以L表示,单位为m。

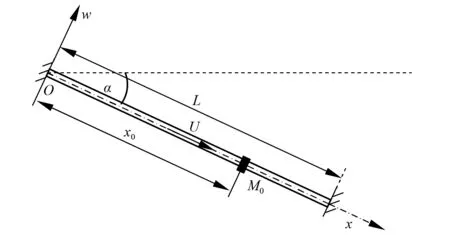
图1 含集中质量的斜置输流管路的力学模型

一般而言,如果不计轴向张力、内部压力、管路材料的能量耗散、管路和流体间的阻尼等因素,输流直管的横向振动微分方程可表示为

式中:E为弹性模量,N/m2;I为横截面惯性矩,m4;w为截面的横向位移,m;x为位置坐标,m;t为时间,s;mf为单位长度流体的质量,kg/m;mp为单位长度管路的质量,kg/m;U为横截面内流体的平均流速,m/s。

在式(1)中,等号左端从左至右依次表示管路的弯曲回复力,流体的离心力,流体的科氏力以及管路和流体的惯性力。该式适用于水平放置且在力学模型上与Euler-Bernoulli梁相近的管路系统。而当管路倾斜放置时,需要计入管路连同流体微元以及附加质量的重力对横向振动的影响,为便于描述,将重力沿管路轴线方向和与之垂直的法向分解为两个分力,则上述影响主要体现在:

(1)重力在轴线方向的分力引起的附加力[14],并且在法线方向产生分力;

(2)附加质量引起惯性力发生变化和产生转动惯性力[15]。

因此,以上两个因素引起的附加项可以表示为

(2)

式中:Γ=mf+mp+M0δ(x-x0);M0为附加质量,kg;J0为转动惯量,kg·m2,其定义为集中质量与它在转动过程中回转半径的平方的乘积;g为重力加速度,m/s2;x0为附加质量的安置坐标,m;α为管路的倾斜角度,rad。

将式(2)代入式(1),于是图1所示管路的控制方程可以表示为

从微分方程的角度来看,式(3)所描述的非齐次偏微分方程与对应的齐次方程的通解一致。而且,从振动力学的角度来看,考虑到管路中心线的法向分力仅能影响振动的平衡位置而与系统的固有特性无关,因此,为了求式(3)的通解,可将其改写为

(4)

式(4)的无量纲形式为

式中:κ=λ+γδ(ξ-ξ0);ε=γδ(ξ-ξ0)/λ。且各参量的定义为

(6)

对于如图1所示的两端固定式输流直管,其无量纲的边界条件可以表示为

η(0,τ)=η′(0,τ)=η(1,τ)=η′(1,τ)=0

(7)

2 Galerkin法推导特征方程

式(5)的解可由Galerkin法表示为

(8)

式中:N为形函数的个数;φn为第n个形函数;qn为与之对应的时间相关项。

将式(8)代入式(5),可得

(9)

分别将各形函数与式(9)相乘并将结果关于ξ在区间[0,1]内积分,经过整理可得

(10)

其中,

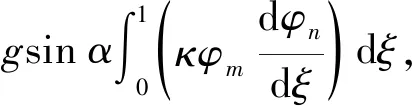
经过整理,式(10)可以表示为

(11)

式(11)的解可以表示为

q=q0exp(iωτ)

(12)

将式(12)代入式(11),经过整理可得

[K+iωG-ω2M]q0=0

(13)

因此,为了得到q0的非平凡解,需满足

|K+iωG-ω2M|=0

(14)

式(14)即为求解系统特征值的特征方程。由上述推到过程可知,为了最终求解式(14),需要知道形函数向量的具体形式,本文采用赵千里等研究中的形函数表达式,即

φn=anξn+1(1-ξ)2, (n=1, 2, …,N)

(15)

其中,

形函数向量则表示为

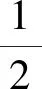
(N+2)(N+3)(N+4)ξN+1}T

(16)

将式(15)引入式(9)～式(14)便可得到系统的特征值。根据上述过程,可知特征值ωj(j=1,2,3,…)仅与E,I,L,U,mf,mp,M,x0和α等系统参数有关且必然为复数,据孙志礼等所述,它的实部表示系统的固有频率,虚部与系统的阻尼有关。

3 计算结果与分析

以某段两端固定式输流直管为例,其中,管路部分的已知参数包括:长度L=1 000 mm,弹性模量E=2.06×1011Pa,密度横截面内、外圆半径分别为r1=12 mm,r2=14 mm,密度ρp=7 800 kg/m3,而管路内部的流体为水,密度ρf=1 000 kg/m3,经式(6)参量的定义计算,质量比β=0.262。赵千里等验证了当函数个数N=8时,本文方法与格林函数法的解已经十分相近,随着N的增加,本方法的计算结果将无限接近精确解。综合考虑计算精度和计算效率,下面的计算均取N=8。下面研究分别固有频率与倾角和集中质量的关系(过程中,出于贴近工程实际的考虑,任取水的流速U=35 m/s),临界流速与倾角和集中质量的关系,且如无特殊说明,所有参数均采用无量纲的形式。

3.1 固有频率与倾角的关系

下面计算当γ=μ=0.01,且ξ0=0.4时,倾角α变化时系统的前四阶固有频率随倾角的变化关系,结果如表1所示。

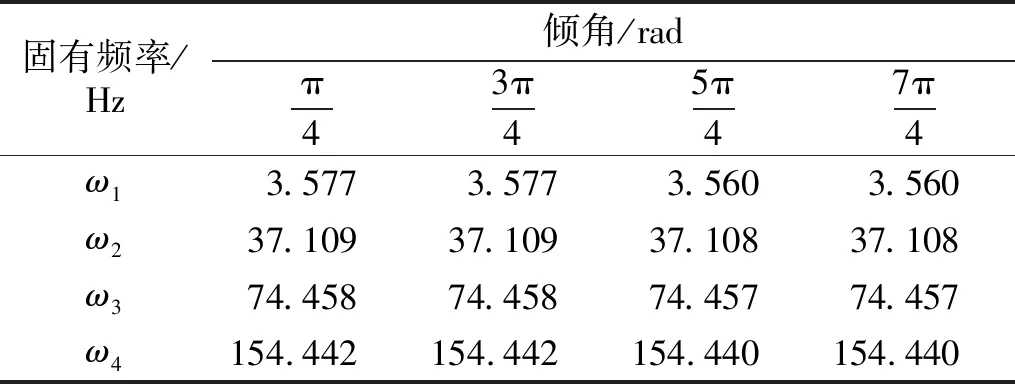
表1 固有频率随倾角的变化

如表1所示,由于原始计算数据的原因,导致当倾角α变化时,各阶固有频率的变化并不明显,但依然能够发现:当管路向下倾斜(即α<π)时,计算结果比向上倾斜(即α>π)时的大,意味着同等参数水平下,向上倾斜的管路的刚度更低。

3.2 固有频率与集中质量的关系

(1)固有频率与γ和μ的关系

取α=0,ξ0=0.2,且其余参数不变,通过计算,得到固有频率随γ和μ的变化曲线,结果如图2所示。

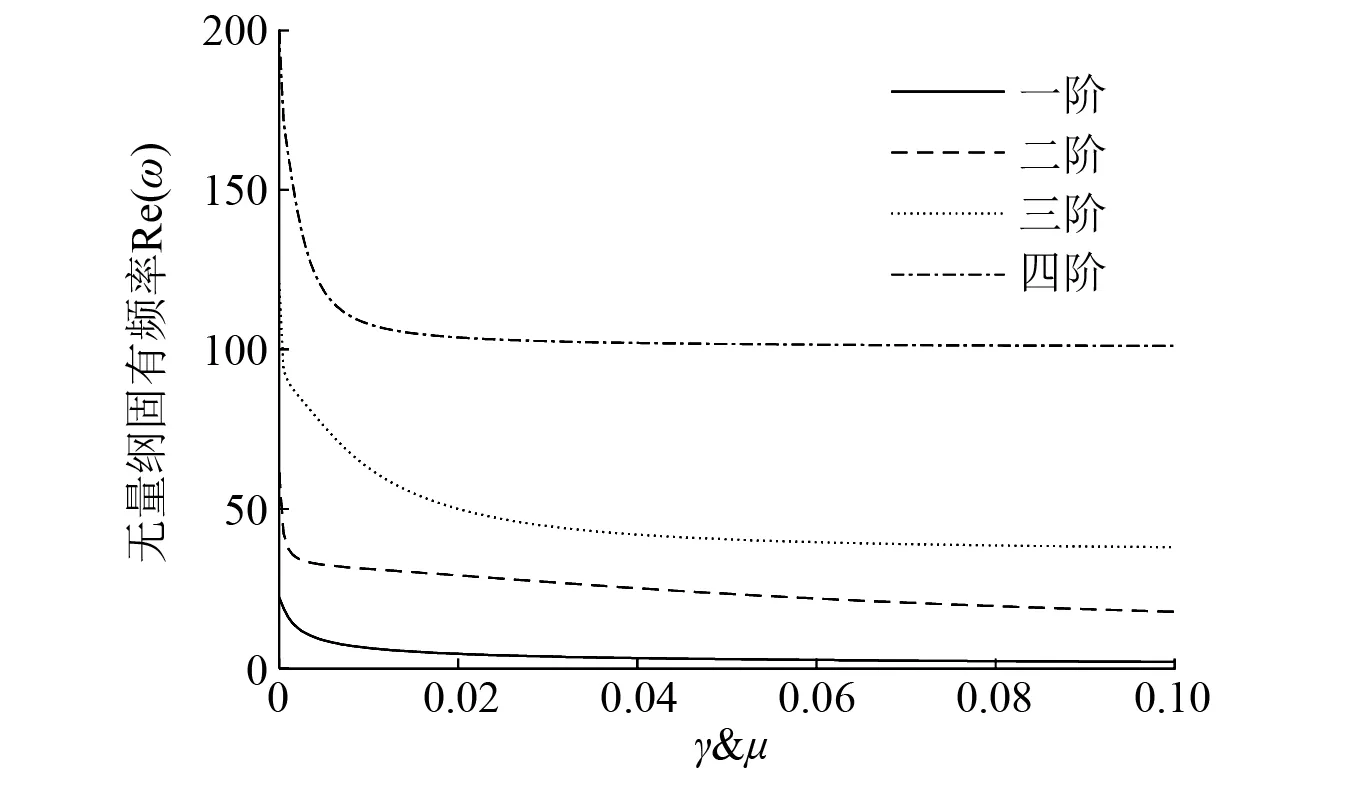
图2 固有频率随γ和μ的变化曲线

由图2发现,随着γ和μ的增加,所有前四阶固有频率在最初阶段均急速减小,而后减小趋势放缓。

(2)固有频率与ξ0的关系

取α=0,γ=μ=0.01,且其余参数不变,通过计算,得到固有频率随ξ0的变化曲线,结果如图3所示。

图3 固有频率随ξ0的变化曲线

由图3发现,随ξ0的增加,固有频率产生波动形式的变化,此外,由于此处管路两端的支承形式均为固定式,导致计算结果关于ξ0=0.5对称。

3.3 临界流速与集中质量的关系

(1)临界流速与γ和μ的关系

取α=0,ξ0=0.2,其余参数不变,通过计算,得到在不同组γ和μ的前提下固有频率随流速的变化曲线,结果如图4所示。

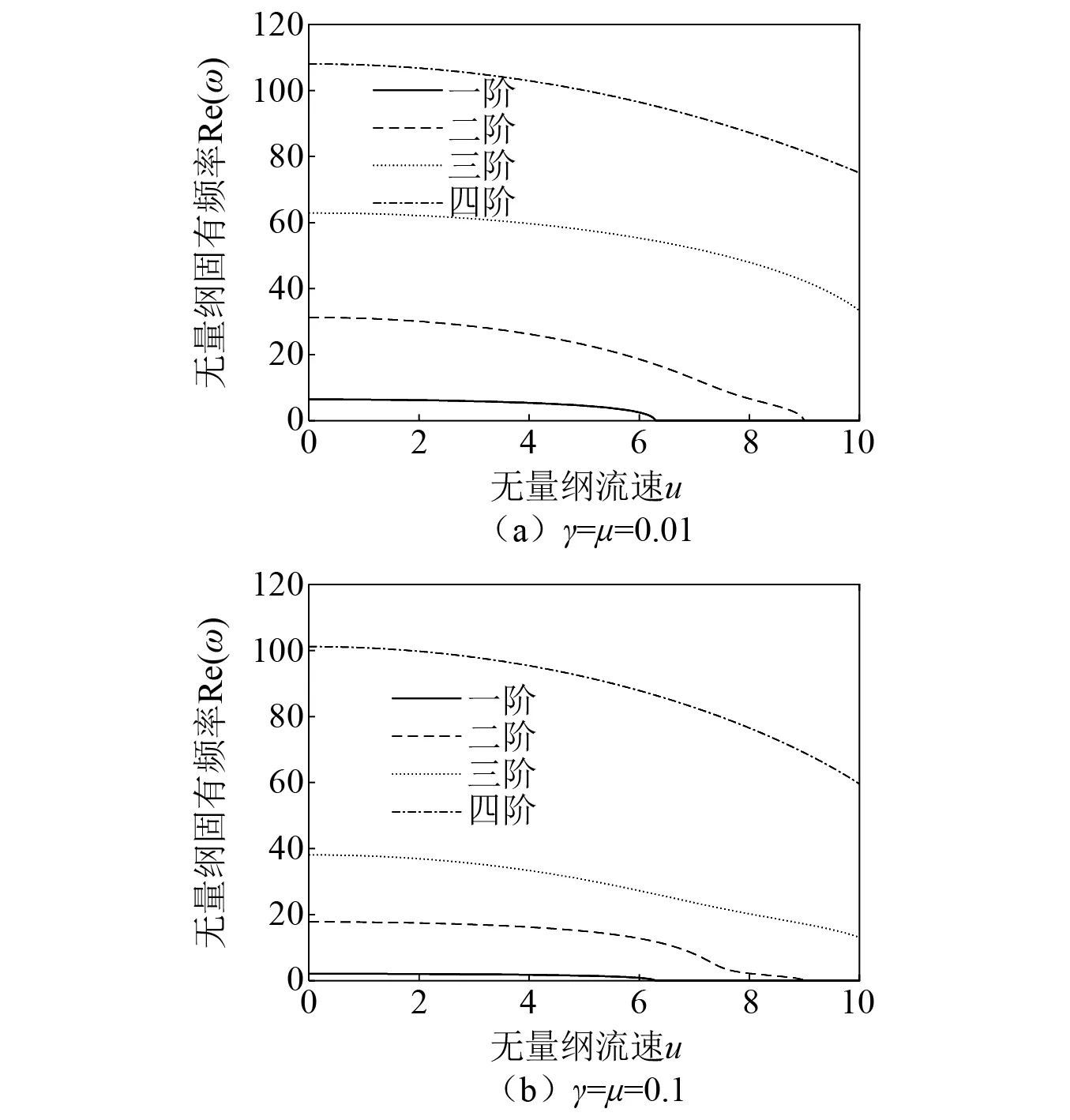
图4 不同γ和μ下固有频率随流速的变化关系

根据图4可以发现:①随着γ和μ的增加,在未发生任何形式的失稳前,所有固有频率均减小;②当γ和μ继续增大,前两阶模态的发散失稳临界流速始终保持不变,其中,一阶对应u1=6.284,二阶为u2=8.987。

(2)临界流速与ξ0的关系

取α=0,γ=μ=0.01,且其余参数不变,通过计算,得到在不同ξ0的前提下固有频率随流速的变化曲线,结果如图5所示。

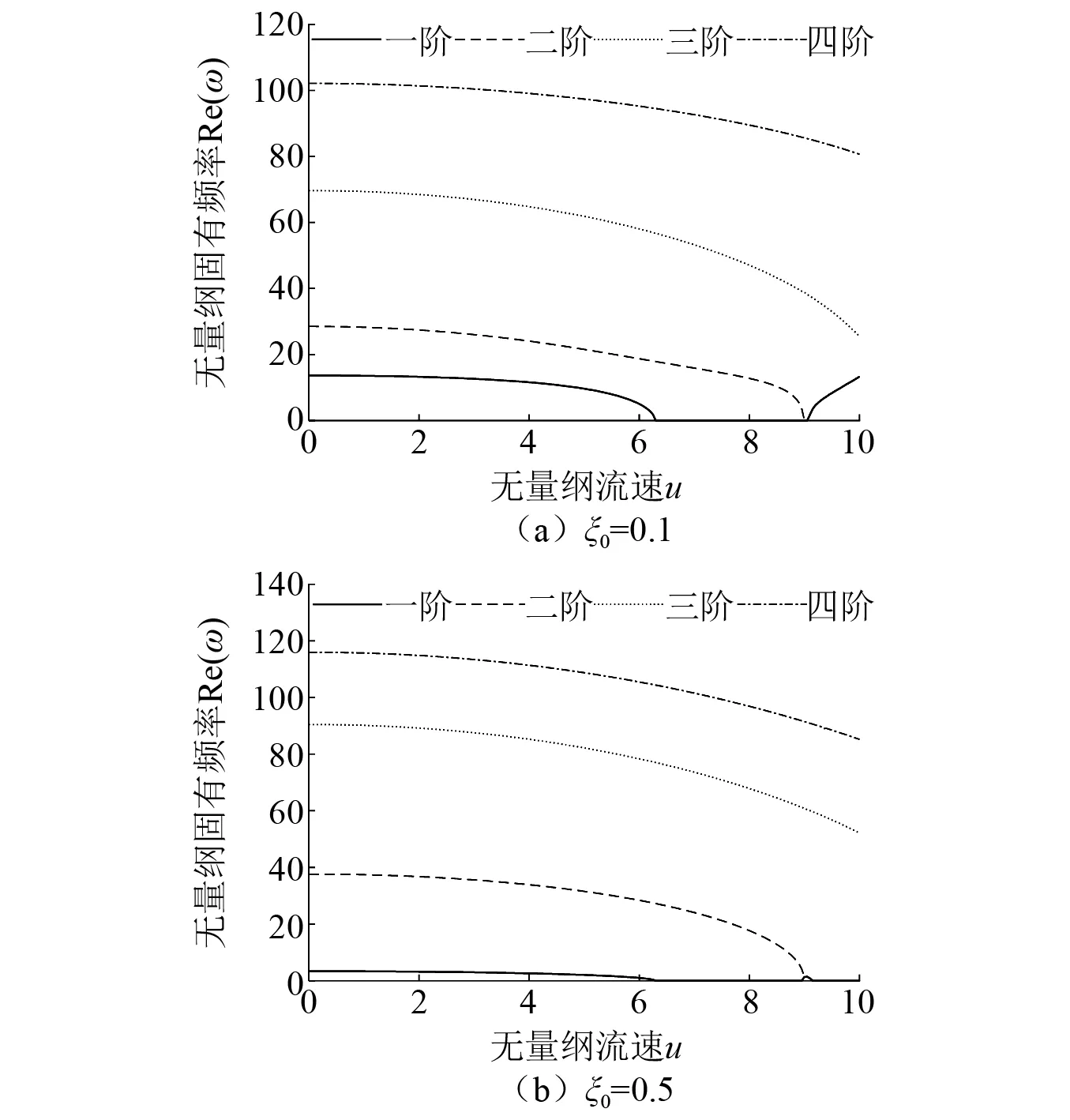
图5 不同ξ0下固有频率随流速的变化关系

由图5结合图4(a),发现无论ξ0如何变化,一阶模态发散临界流速始终保持u1=6.284不变,但在此临界值以后出现的失稳形式有所差异,具体表现为:当ξ0=0.1时,二阶模态首先出现发散,且临界流速为u2=8.987,之后在u=9.084开始一阶、二阶模态合二为一;而当ξ0=0.2时,仅二阶模态发生发散失稳,且与之对应的临界流速仍为u2=8.987,之后直到u=10,一阶、二阶模态始终处于发散状态;但是,当ξ0=0.5时,由于一阶模态发散的提前结束,二阶模态在未发生发散时便与一阶模态耦合,发生颤振,与之对应的流速的临界值为uc=8.976,之后二者合二为一,然后在u=9.121再次发散。

4 结 论

(1)通过引入重力和倾角这两个因素,建立了含集中质量的斜置输流直管的横向振动微分方程,利用基于新型形函数的Galerkin法对该微分方程进行了离散,推导得到了计算管路固有频率的特征方程。

(2)经过实例计算,发现:同等参数水平下,向上倾斜的管路的刚度更低;随集中质量的增加,在既定的流速下,固有频率首先急速减小,然后趋势放缓,但集中质量的改变不会影响发散临界流速的计算结果;随集中质量安置坐标的增加,在既定的流速下,固有频率波动变化,且安置坐标能够引起临界流速和失稳形式的变化。

(3)研究可被借鉴用于研究具有其他支承形式、附加元素的管路的流固耦合振动问题,为后续的振动可靠性等问题的研究作了良好的理论及计算方法方面的铺垫。