单元整体教学中大概念“锚点”价值的分析与应用
——以“长方形和正方形的面积计算”课时为例
2023-10-31苏州大学附属吴江学校215006
苏州大学附属吴江学校 (215006) 顾 健
淮阴师范学院 (223300) 任建波
按照整体论的观点,学习应该被视为一个具有内在生成性的自然整体,这意味着学习应该是以整体的方式进行,而不是分而习之。大概念统摄的单元整体教学设计为学生开展“整体的方式”学习提供了可能。开展大概念统摄的单元整体教学,首先需要对单元进行整体教学分析,既包括解读教材、提炼大概念,又包括研究学生、分析学生学习起点,在此基础上,依据大概念的中心性、可持久性、网络状和可迁移性等特征,将大概念的“锚点”价值充分彰显,并渗透和应用到学习活动的联结、过渡和建构之中。本文以苏教版教材三年级下册第六单元“长方形和正方形的面积计算”一课为例,在分析单元整体教学中大概念“锚点”价值的基础上,对课时教学进行实践探索。
一、单元整体教学分析
1.解读教材、提炼大概念
本单元是平面图形面积计算的起步,从一维的度量转到二维的度量,起着承上启下的作用。从知识脉络上看(如图1),知识点在教材上呈线性排列,将面积单位的教学分为两段,中间穿插面积计算,这是因为面积单位之间的进率很难从面积单位本身得出,借助正方形面积更容易理解。教材的编排关注了单元结构,但是前后知识和方法的关联略显不足,比如,长度、角、体积的度量本质都是单位个数的累积,如果不将其置于更大的视野中,学生难以形成“度量”的上位概念并搭建整体迁移的支架。

图1 教材内容分析
基于以上分析,结合《义务教育数学课程标准(2022 年版)》对相关内容的要求,可提炼出本单元的大概念:面积是“数”单位面积的个数,图形面积具有可加性。在前后知识的相融互通中理解面积,增强几何直观和推理意识等。
2.研究学生、分析学习起点
选取本校三年级5个班学生(共196名)进行前测,测试内容和相关结果如下。
前测题1.观察下面的生活现象(如图2、图3),用笔涂一涂、画一画或写一写,表示它们的不同。

图2 粉刷墙面

图3 栅栏围地

表1 前测题1的测试结果
【分析】从统计结果来看,能识别“面积”的学生占比高达65.3%,这主要有两个原因:一是生活中有接触,如“我的手掌比你的大”“我家电视机屏幕比教室里一体机的小”,学生的表达体现了对“面积”的初步感知;二是教材中的渗透,如一年级下册“认识图形”单元习题“在正方形、长方形、三角形和圆里分别涂不同的颜色”已经孕伏“面积”的意义。
前测题2.图4 中的小正方形表示1 平方厘米,①②长方形的面积分别是多少?
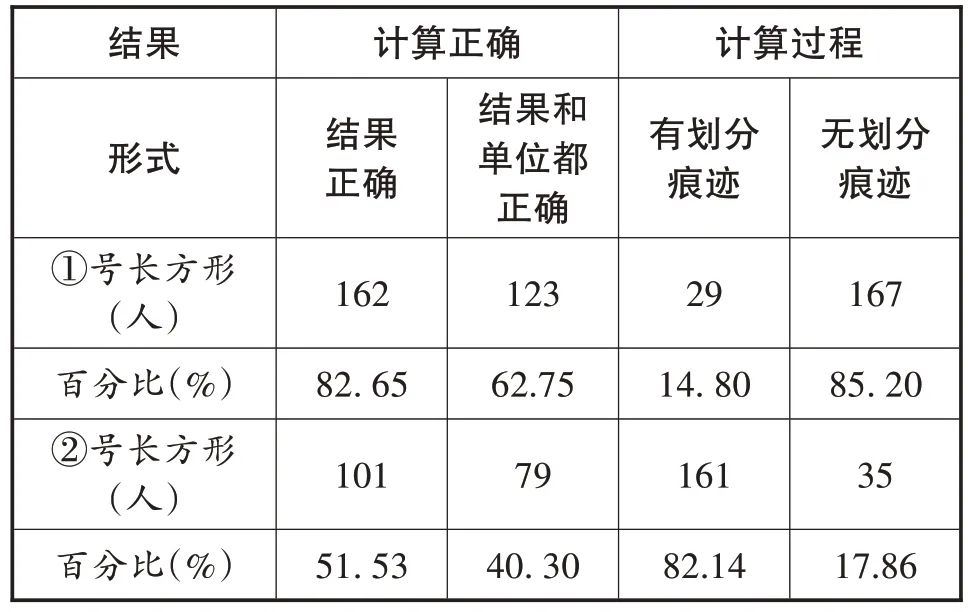
表2 前测题2的测试结果

图4
【分析】统计结果表明,学生借助单位面积用“全覆盖”方式求①号长方形的面积的正确率达82.65%,而利用“沿边摆放”方法求②号长方形的面积的正确率只有51.53%,说明学生自主探究有一定的困难。进一步分析,有82.14%都采用了划分单位面积的方法,说明教师要关注这一年龄阶段学生直观想象和推理能力的培养。
前测题3.你会计算图5 中长方形的面积吗?请列式并说明理由。

表3 前测题3的测试结果

图5
【分析】从数据上看,一旦没有“单位面积”辅助思考,学生的计算正确率骤然下降,只有65.81%,其中,计算正确的学生中有48.06%对长方形进行了划分。虽然前测题2 已有暗示,但是学生并不能建立单位面积的个数与长、宽数值之间的联系。这说明教学中要重视长方形面积计算的推导过程,引导学生感悟长度、周长、面积等度量方法的内在一致性。
不难发现,很多学生已经知道了长方形的面积计算方法,但是对“面积大小和计算”的认识仍然浮于表面,难以迁移和感受度量方法的一致性。教学中要着重引导学生经历用面积单位度量长方形的过程,关联线段的“测量属性”,进而推导出长方形和正方形的面积计算公式,为学生后续学习角、圆的面积、长方体的体积做铺垫。
二、教学活动实践
[片段1]关联旧知,激疑启思
师:还记得怎样测量线段的长度吗?(出示图6)请说一说测量的过程。

图6
生1:用1 厘米的线段去量,4 个1 厘米就是4厘米。
师:线段长几个1 厘米就是几厘米。如果想知道图7中图形的面积大小,首先要知道什么?
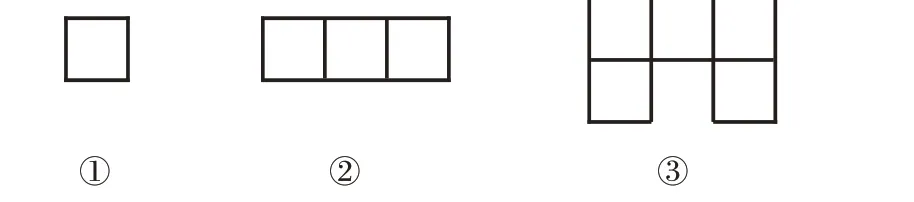
图7
生2:知道一个小正方形的面积是多少。
师:如果一个小正方的面积是1平方厘米,图7中图形的面积分别是多少?
生3:分别是1 平方厘米、3 平方厘米、5 平方厘米。
师:你是怎么想的?
生3:每个图形中有多少个面积是1 平方厘米的小正方形,面积就是多少平方厘米。
[设计意图]通过对测量线段长度方法的回顾,使得学生的度量经验自然迁移到面积测量之中,学生初步建立“单位测量属性”的知识锚点。在判断图7②、③图形面积时,学生还发现,虽然形状不同,但是都与小正方形的个数有关,由此感知面积的可度量属性。
[片段2]实验操作,探究规律
师:利用1 平方厘米的透明方格纸,拼出一个长方形,并记录在学习单上(见表4)。

表4 学习记录单
师:观察表格,说一说你的发现。
生1:我摆的长方形有4 排,每排有5 个,一共有20个1平方厘米的小正方形,这个长方形的面积是20平方厘米。
生2:我发现长方形的面积与小正方形的个数相同。
师(出示图8):根据同学们的发现,可以用这样的方式表示它们的关系。
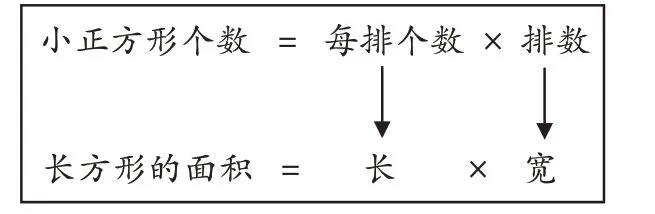
图8
[设计意图]学习单给出了思考和观察的路径,让探索有方向。学生在操作中感受到长方形的面积与小正方形(单位面积)个数之间的关系,学习单为聚焦面积概念的本质提供了丰富的表象;通过观察、说理,学生发现了每排个数与长之间的联系、排数与宽之间的联系;通过推理,学生验证了长方形的面积与单位面积个数之间的关系。虽然从前测的结果来看,“算”更接近学生的思维实际,但是很多学生对面积的理解还是停留在了数值上的相等。
[片段3]抽象推理,得出模型
师(出示长为4 厘米,宽为3 厘米的长方形图片,图略):根据刚才的结论,测量出这个长方形的面积至少需要多少个面积为1 平方厘米的小正方形?
生1:不用铺满,只需要沿着它的长摆4 个,沿着它的宽摆3个,一共需要6个小正方形,长方形的面积是4×3=12(平方厘米)。
生2:如果不怕麻烦,只需要一个小正方形,一边铺一边画线,同样能算出长方形的面积是12 平方厘米。
师:如果没有小正方形,怎么能知道这个长方形的面积?
生3:可以用尺子量一量,长是4 厘米,宽是3厘米,4×3=12(平方厘米)。也就是每行可以画出4个1厘米的小正方形,一共有3排。
师(出示图9):回顾刚才的学习过程,从最初的铺满,到铺一部分,到边铺边画,最后直接量出长和宽,计算出长方形的面积,我们推导出的长方形的面积计算方法是什么?

图9
生4:长方形的面积=长×宽。
师:如果长方形的长用字母a表示,宽用字母b表示,长方形的面积计算可以用字母表示为S=a×b。
[设计意图]这一环节把密铺和测量联系在一起,学生在“操作—想象—符号表征”的过程中能够提高数学思维力。在进行“部分铺”的操作中,学生感知了长方形的面积与长、宽相关;在“边铺边画”的想象中,学生明确了二维图形的面积需要两个一维线段长度的数值进行刻画;在总结计算公式可用符号表征的推理中,学生经历从“特殊”到“一般”,体会符号表征的简洁性。在整个过程中,学生理解了面积的内涵,实现了从操作的“实践表征”向“空间想象”的迈进。
[片段4]运用模型,体会一致
师(出示图10):只能用边长为1厘米的正方形测量长方形或正方形的面积吗?能不能用给定的正方形量一量长方形的面积?

图10
生1:边长为1 厘米的正方形面积是1 平方厘米,所以图形①的面积是4×3=12(平方厘米),图形②的面积是8×4=32(平方厘米);边长为2厘米的正方形面积是4 平方厘米,测量图形②的面积时一共摆8 个,所以图形②面积是4×8=32(平方厘米),但是测量图形①时,不能正好摆满。
师(出示图11):测量图形的面积和测量线段的长度之间有什么相同的地方吗?

图11
生2:测量线段是看有几个长度单位;测量面积是看有几个面积单位。
师(出示图12):在以后的学习中,测量物体的体积还会用到这样的方法。

图12
[设计意图]学生通过比较,发现用边长为2 厘米的正方形测量图形②更方便,但是测量图形①却有困难。用边长为1 厘米的正方形既能测量图形①也能测量图形②,在对比中从度量角度理解了像1 厘米、1 分米,以及1 平方厘米、1 平方分米这些数学中规定的常用长度和面积单位有其合理性,是选择的结果。
三、教后反思
一般来说,儿童建构“面积测量”这个“概念”需要经历三个阶段:首先,6 岁左右的儿童可以在具体操作活动中建构面积守恒的观念;其次,10 岁左右的儿童可以通过操作活动“发明”测量各种规则平面图形面积的方法;最后,12 岁左右的儿童可以用纯粹形式化的代数推理得出各种平面图形的面积公式。
为了更精确地了解三年级学生的学习起点,通过前测了解学生对“面积”相关知识的掌握现状,如混淆周长和面积的概念、会计算方法却道不明理由等。在此基础上,教师从学生的“已知”“已会”出发,重整教学资源,使学生在回顾测量长度的经验的过程中初步感悟“单位测量属性”;在操作活动中体悟数值相等背后是“单位面积个数”与“长方形面积”的对应关系;在推理思辨中领悟如何用“一维线段”刻画“二维面积”;在拓展运用中以整体视角深刻理解线、面、体的“锚点”——单位的可累积性。“学”是“需求侧”,表明在哪里;“教”是“供给侧”,指向去哪里。只要立足学情调研、资源调配,抓住大概念的“锚点”,就能让教学预期“可及”,也能实现“学”与“教”的“共振”。
