大概念视角下运算本质一致性教学探索——以“小数乘整数”为例

苏州大学附属吴江学校 （215006） 顾 健

淮阴师范学院 （223300） 任建波

【课前思考】

“小数乘整数”是苏教版教材五年级上册第五单元第一课时的教学内容，以往的教学目标是“学生能凭借整数乘法的计算方法或运用积的变化规律计算出结果，进一步可以总结出小数与整数乘法之间的关系”。在深入学习《义务教育数学课程标准（2022 年版）》的相关课程理念与教学建议后发现，以往教学目标中追求学生计算方法的熟练并不能证明学生对算理已经有了通透的理解，指向学生数学运算能力的形成尚有空间。此时，如果独立地看待这一课时，可以通过“整数乘法”——“求几个相同加数的和的简便计算”类推到“小数乘整数”，但是在教学“小数乘小数”时，比如“0.1×0.2=”，学生会因为两个因数都是小数而产生认知偏差，以致不能准确理解其得数0.02是单位细分的结果，产生了迁移单一、片面的现象。这限制了学生知识理解和认知发展的全面性、整体性需要。

大概念不仅仅能够促进学生对于知识纵向上的本质理解以及横向上的联结扩展，还能够发展学生自我建构与自我进化的能力。从运算教学角度来看，这个课时既独立又与前后知识关联，可以看成是基于大概念统摄来形成知识链、建构知识体系和认知体系的“锚点课”。对此，需要思考：如何提炼出属于这个课时的大概念，并在单元整体视角下将其自然、无痕地融入学生的迁移性学习？进而利用运算意义支撑“算法”的多样性，使学生能在不同“算法”的背后探寻其本质，大胆构建可迁移的路径。

基于以上思考，笔者对这个课时的教学做了如下梳理（如图1）：

图1

【课堂实践】

一、激活经验，理解意义

师（出示情境图，如图2）：从图中可以知道哪些数学信息？

图2

生1：夏天时，每千克西瓜0.8 元；冬天时，每千克西瓜2.35元。

师：夏天是西瓜成熟的季节，购买3 千克西瓜需要多少元？请列算式。

生2：0.8×3。

师：说说列乘法算式的理由。

生3：每千克0.8元，3千克是3个0.8相加，可以列式0.8×3。

生4：根据数量关系“单价×数量=总价”。

师：是的，既可以联想到整数乘法的意义——小数乘法也是求几个相同加数的和，也可以联系数量关系，得出算式。

【设计意图】教材的情境设置贴近学生日常生活，有利于学生在真实情境中获得感悟。学生对小数乘法有一定的认知经验，这一环节主要是沟通整数乘法与小数乘法意义之间的联系，引导学生通过数量关系列出乘法算式。这样既能连接新知与学生的认知起点，也有利于学生积极、主动地展现思维过程。

二、理解算理，构建概念

师：怎么计算0.8×3？

生1：把0.8×3 看成0.8+0.8+0.8，也就是3 个0.8相加，和是2.4。因此0.8×3=2.4。

师（出示图3）：利用小数加法和小数乘法之间的关系进行推理是个好办法！

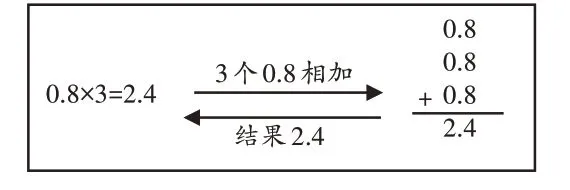
图3

生2：把0.8元看成8角，这样就变成了整数乘法8×3=24（角），再把24角换算成2.4元，所以0.8×3=2.4。

师（出示图4）：借助已经学过的“元、角”知识，将小数转化成整数再进行计算，你真会思考！

图4

生3：还可以把0.8 扩大10 倍，看成8。我们会计算整数乘法，想8×3=24，再把得到的结果24除以10，是2.4，所以0.8×3=2.4。

师（出示图5）：利用积的变化规律进行计算，一个因数乘10，另一个因数不变，积除以10，得到的积大小不变。比较这两种计算方法，有什么相同的地方吗？

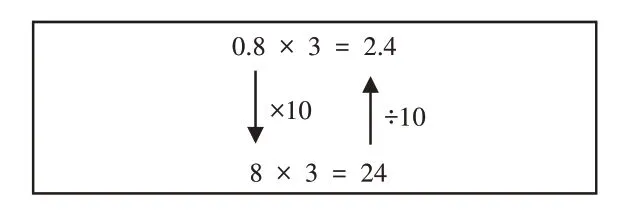
图5

生4：一种是单位换算，另一种是积的变化规律，它们都是把小数乘法转化成整数乘法进行计算。

师：会观察，善总结，还有其他方法吗？

生5：还可以列竖式计算。0.8 是8 个0.1，乘3，得24 个0.1，所以0.8×3=2.4。还可以变竖式为横式，用乘法分配律。

师（出示图6）：结合图示更方便理解。每个正方形表示1，平均分成10份，每一份是0.1，其中的8份是0.8。0.8×3表示这样的几份？是多少呢？

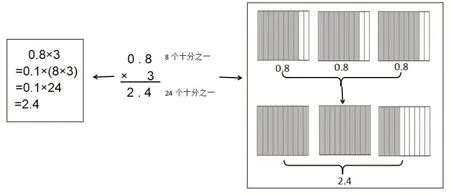
图6

生6：表示这样的24份，是24个0.1，就是2.4。

生7：0.8 表示8 个十分之一，乘3 得到24 个十分之一，也就是2.4。

师：这样看来，可以先算8×3=24，表示这样的24份，从图示可以看出，合起来是2.4。竖式计算是有道理的！

师（出示图7）：这两种竖式书写方法，哪一种更合理呢？

图7

生8：我觉得第②种更合理，在进行加法竖式计算时，要求数位对齐。

生9：我觉得第①种更合理，在计算整数乘法时，要末尾对齐。

师：听着都有道理，这可怎么办？

生10：我也支持第①种写法。因为刚才用单位换算、积的变化规律计算时，都把小数0.8看成整数8，再乘3，这样就看成整数乘法，所以8 和3对齐。

师：对比研究是个好办法！加法计算中只有相同数位对齐才能相加；小数乘法转化成整数乘法，所以末尾对齐更方便计算。我们习惯用第①种方式。

【设计意图】本环节注重联系学生已有知识，在追问中激活学生的已有经验，在质疑中激发学生主动建构算法。首先，从小数乘整数的意义入手，学生自然能想到用“连加”解决问题。其次，学生从单位换算角度将小数0.8 转换为整数8 后，初步体悟小数乘法与整数乘法之间的关系。最后，学生从积的变化规律和乘法结合律角度理解小数转化成整数的合理性。多样的算法表征促使学生在同化和顺应中完善已有认知，逐渐建立起小数乘法的计算结构。而利用竖式计算，借助图形直观展现算理，“算法抽象”建立在“算理直观”基础之上，能贯通多种表征形式，为学生理解两位小数乘整数的方法做铺垫。

三、沟通算理，归纳算法

师：冬天时，西瓜价格发生了变化。买3 千克西瓜要多少钱？6元够吗？

生1：2×3=6，2.35大于2，6元肯定不够。

师：估算是个办法，买3千克究竟需要多少钱？

生2：先算235 乘3，3 乘个位上的5，得15，写5向十位进一；再用3乘十位上的3，得9，加上进上来的1是10，写0向百位进一；然后用3乘百位上的2，得6，加上进上来的1 是7，得705 后；最后，添上小数点是7.05。

师：刚才计算0.8×3 时，得数2.4 是一位小数，2.35×3 得数7.05 是两位小数。7.05 的小数点位置是怎么确定的？

生3：2.35 表示235 个百分之一，再乘3，得到705个百分之一，所以是7.05。

师：回答得有理有据。现在回头看这两道小数乘整数的竖式计算（略），它们在计算方法上有什么相同之处吗？

生4：都是先看成整数乘法进行计算，算出得数后再添上小数点。

生5：列竖式时，都是末尾对齐。

生6：一位小数乘整数，得数是一位小数，两位小数乘整数，得数是两位小数。

师：顺着生6的思考，你还能联想到什么？

生7：几位小数乘整数算得的积就是几位小数。

【设计意图】本环节重点解决两个问题，一是通过对小数乘整数意义的理解确定积的小数点位置。在计算得出705 后利用问题“7.05 的小数点位置怎么确定的？”帮助学生回到源头进行思考。二是概括小数乘整数的计算方法。先通过比较两道竖式，从形式上判断出小数位数与积的位数关系；再通过类比推理，感悟一位小数乘整数就是计算有多少个十分之一，两位小数乘整数就是计算有多少个百分之一，依此类推，几位小数乘整数的实质是计算有多少个单位“1”。这样的过程，既有算理思考的深度，又有算法概括的高度。

四、变式练习，灵活应用

师：根据148×23=3404，能直接写出“14.8×23”“148×0.23”“1.48×23”的积吗？

生1：14.8×23=340.4。

生2：148×0.23和1.48×23的积都是34.04。

师（出示图8）：有意思！算式不同结果却相同，这是巧合吗？

图8

生3：都是两位小数乘整数，结果也都表示3404个百分之一，积当然也相同了。

师：数学是讲道理的，你一下就找准了问题的关键。根据上面的算式，再写一道得数是340.4 的算式。

生4：148×2.3。

师（出示图9）：请计算这个竖式。

图9

师：35×0.24，其中一个因数是两位小数，积怎么是一位小数呢？

生5：先算35×24=840，点上小数点，根据小数的基本性质，末尾去掉0，小数的大小不变。

【设计意图】改编教材中的一道习题，目的是让学生对因数与小数点之间抽象关系的理解具体化。得出3 道算式结果后，学生在问题“为什么算式不同，结果却相同？”中进一步理解了算法。随后，在比较中引起认知冲突——“其中一个因数是两位小数，积怎会是一位小数呢？”，使学生感受如何运用新知解决问题。

五、拓展延伸，整体关联

师：今天学习了小数乘法，之前学过整数乘法，上一单元还学了小数加法，比较一下，它们有什么相同之处吗？

生1：整数乘法的结果表示几个一、几个十、几个百……

生2：小数加法和小数乘法的结果表示几个十分之一、几个百分之一……

师：一、十、百……，十分之一、百分之一……都是什么？

生3：计数单位。

师：是呀，其实不管哪一种计算，它们的共同之处都是计算有多少个计数单位。

【设计意图】本环节通过对不同“数”运算的回顾，引领学生体会不同“数”运算的内在一致性，帮助学生建构整体认知，实现对小数乘法的深度理解。

【教后反思】

大概念在整个知识结构和学生认知系统中均具有很强的附着力，依托大概念可以在原有的知识和现有的知识之间，以及在学生旧的认知结构和新的认知生长点之间都能找到同化和顺应的“锚点”。在计算教学体系中，小数乘整数与整数、分数乘整数有何异同？本次的教学探索得出以下两点：

第一，多元表征，寻关联。从学生熟悉的情境出发，从乘法的意义、计量单位的转化、积的变化规律等角度，顺其自然地归纳出0.8×3 都是转化成8×3进行计算，进而借助乘法结合律进行推演，即0.8×3=0.1×（8×3）。为了方便学生更直观地理解，笔者展现了3 个0.8 通过累加变成2.4，也就是24 个0.1。至此，学生的关注点聚焦在“计数单位”上，实现了从对运算本质的认识回溯到对数的认识上（数的组成）。

第二，回归原点，定“锚点”。在计算两位小数乘整数时，学生能从计数单位的角度进行解释，体现了大概念的灵活性与可迁移性。练习中，根据整数乘法的结果深度探究另外三道算式，数字虽不同结果却相同的过程，推动了学生运算思维的进阶可视化。更难能可贵的是，总结时，学生在整数乘法、小数乘法、小数加法计算体系中感受到了知识迁移过程中“锚点”（计数单位）的固着力。可见，教学建立在这个大概念基础上，有效降低了学生的思维负荷，拓宽了学生认知运算本质的“算理域”，丰富了学生掌握运算技能的“方法场”。