联系观指导下的概念课教学体验

孙磊

【摘要】数学知识的连续性和结构性与课堂教学的片段性和分散性是传统教学中常见的一对矛盾.用联系观指导的教学设计旨在启发学生用联系的观点看待数学问题，认识数学的整体性，是弥补传统教学短板的有效方法.学生在理解新知的同时获得相关的研究经验，有利于完善基于联系观和发展观的思维方式，整体把握分数指数幂的学习，促进学科核心素养的落实.基于此，笔者以“分数指数幂”一课的教学为例，谈谈自身对联系观指导下的高中数学教学设计的认识和体会，供大家参考.

【关键词】联系观；教学设计；核心素养

一、问题的提出

数学知识并不是孤立的存在，往往具有高度的系统化和结构化特征.虽然知识需要一点点积累，但是教学却不能简单地将数学拆分成一个个零碎的知识块去装进每一节课堂.唯物辩证法提出用普遍联系的观点看世界，反对用片面或者孤立的视角去看待问题.数学学科知识的整体系统蕴含着丰富的唯物辩证观.《普通高中数学课程标准（2017年版2020年修订）》指出课堂教学应该突出数学主线，凸显数学的内在逻辑和思想方法.要做到这一点，就要深入数学内部，明确知识间的内在逻辑关系，把握数学本质，突出数学的思想方法.

联系观指导下的教学重在“联系”.通常情况下，联系又分为横向联系和纵向联系两种形式.横向联系立足于知识的前后关联与逻辑线索，从学生已具备的认知基础去寻找新知识的发生点，让数学问题的呈现和解决更加自然.纵向联系则立足于数学思想方法、学科素养的类比进而拓展，能够使教学所呈现的认知方式获得学生的更多认同，真正做到渗透思想方法.

分数指数幂是一类重要的运算符号表征，有着广泛的应用.人教A版教材的编排是通过类比整数指数幂的运算法则，给出分数指数幂的运算法则的.传统知识点教学往往忽视整数指数幂与分数指数幂的内在联系，带来的弊端就是重计算轻理解.而以联系观为指导的教学组织实施，对于帮助学生整体构建知识框架、认识指数幂拓展的真正意义有一定的指导作用.

二、课例设计

（一）对根式的探究导入

师：回顾过去的学习经历，以运算为基础的数系扩充我们经历了哪些历程？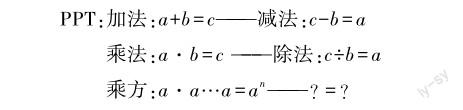

师：乘方是求n个相同数字乘积的运算，它的结果用幂来表示.乘方的逆运算是什么呢？它的结果可以怎样表示？这是我们这节课将要研究的问题.

设计意图：

n次方根在本节课中是一个过渡性概念，为分数指数幂的引出打基础.作为运算符号，它是分数指数幂的另一种表达形式；作为运算指令，它又是乘方运算的逆运算.

设计意图：数学知识的生长存在内部的逻辑需要，相关知识点也存在千丝万缕的联系.

上述过程让学生通过已有知识类比探究得到n次方根的概念，完善学生数学知识系统.

师：我们通过类比的方法得到了n次方根的概念.那么，你们会求a的n次方根吗？

（4）0的负分数指数幂没有意义.

师：以分数作为指数的幂可以用来表示根式，幂的指数范围也由整数扩充到了有理数.整数指数幂的运算性质对于有理数指数幂也同样适用，即对于任意有理数r，s，均有下面的运算性质.

设计意图：由于第（2）题数据复杂，通过定义解题难度较大，分数指数幂的运算性质在简化计算方面的优势顿时凸显出来.

三、教后反思

本节课的主要任务有两个，一是根式的定义；二是分数指数幂的定义及运算.数学概念的产生并不是凭空规定出来的，有其数学本身的发展需求.教师在教授这一内容时不仅要向学生提供前所未有的东西，而且要提供比以往经验更为先进的东西.一方面要规定新的概念，另一方面新的概念又要對原有理论进行更新与完善.教师要精心设计教学过程，帮助学生真正理解分数指数幂的含义，深刻理解研究分数指数幂的思想方法.

（一）善用联系的观点发展思维的成长

教育学家弗赖登塔尔认为：数学学习不是被动的吸收，而是一个以学生原有的知识经验为基础的主动建构过程.高中的数学教学应该关注学生的认知结构和逻辑思维的发展，用联系观指导的课堂教学，对数学教学中的各个要素进行综合考量，不仅帮助学生理解新知，还能使学生获得相关的研究经验.对于提升学生的理性思维有极大的帮助.

本节课在根式的引入和分数指数幂的引入上都打破了教材的设计，从学生已有的认知基础出发，在运算的相逆性和统一性中寻找冲突提出问题.在幂运算法则的框架下，尝试将未知转化成已知，呈现出类比探究的脚手架，使各个层次的学生都能找到解决问题的途径.当然，这个过程对教师的数学素养和整体大局观也提出了更高的要求.

（二）善用联系的观点促进素养的提升

数学素养的提升在于平时课堂的点滴积累，教师首先要做的是发挥学生的主观能动性，让学生成为课堂的主角，通过精彩的教学设计，让学生获得知识联系的同时，对于思想、方法能提升到全局的高度.

对于分数指数幂的引入，教材是通过几道根式化简的例子归纳出一般规律的.由于教材是面向各个层次的学生，其选择的方法更多立足于基础，虽然学生容易接受但是多少缺乏了思维度.同时因为学生知识储备不足，对于总结出来的分数指数幂的意义，也难以证明其是否符合幂的运算法则.在联系观指导下追溯分数指数幂产生的来龙去脉，会发现指数域从正整数扩展到整数、实数，是由于数学内部的需要，其发展历程是在幂运算法则的框架下进行的.因此，笔者设计的课堂探究始终是在学生非常熟悉的知识块中寻找与新知的联系，这不仅符合数学发展路径，也体现了数学规则的合理性.这个研究经历对学生感悟本质、获取研究经验、提升数学核心素养有很大的帮助.

【参考文献】

[1]端木彦.联系观指导下的主题教学设计研究[J].中小学数学（高中版），2020（06）：6-8.

[2]中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）[M].北京：人民教育出版社，2020.

[3]朱正新.基于数学史观的课堂教学设计———以“分数指数幂”为例[J].数学学习与研究，2018（04）：100-101.