基于经验模态分解和支持向量机的日径流预测研究

2023-10-30万新宇王鑫宇侯添甜林晓梦

水力发电 2023年10期

万新宇，王鑫宇，侯添甜，林晓梦

(河海大学水文水资源学院，江苏南京 210024)

0 引言

径流预测是水资源开发利用与管理的重要依据[1]，但径流形成具有显著的非线性特征，预测难度大。因此，径流预测一直是水资源领域研究的热点问题，过程驱动模型和数据驱动模型是当前径流预测常用的两类方法[2]。过程驱动模型建立在流域产汇流的机理上，利用水文学方法对径流形成过程进行模拟，如新安江模型、SWAT模型及TOPMODEL模型等。数据驱动模型则是根据数理统计原理，深入挖掘输入与输出数据之间的相关关系，建立径流预测模型，如多元线性回归[1]、支持向量机[3-6]、神经网络模型[7-10]等，均在径流预测中取得了较为可观的成果。

近年来，随着深度学习理论的快速发展，一种改进的循环神经网络——长短期记忆神经网络(LSTM)在径流预测中得到了较为广泛的应用[7，9-10]，如孙望良等基于DFA-VMD处理的数据集通过LSTM模型对三峡水库进行日径流预测，结果表明其性能优于BP模型[7]。此外，支持向量机(SVM)作为监督机器学习模型可以用于异常值检测以及预测序列，顾哲衍等对黄尾河径流预测研究中发现在高精度模拟上，SVM模型优于BP模型[11]。当前径流预测的研究方向着重于优化模型，以达到更好的预测效果，针对数据驱动模型的输入步长(滑动窗口)的讨论较少，孙传文等通过构建三峡水库的季节性SVM模型进行月径流预测，结果优于BP神经网络模型和标准SVM模型[6]。王爽等通过对历史时间序列进行自相关分析选择最佳输入步长，在最小二乘支持向量机(LSSVM)和LSTM的预测中获得了较好的预测效果[12]。为了能较为清楚直观且有依据地选择输入步长，使用自相关函数分析水文数据的相关性，提高预测精度。

由于水文径流序列具有非线性与非平稳性[13]，单一深度学习预报模型在训练过程中易受噪声信号干扰，导致对时间序列内部规律的变化不能明显识别，影响预测精度。为此，本研究引入一种自适应信号时频分解方法——经验模态分解(EMD)对日径流序列进行分解，识别其内部变化规律，构建基于EMD和SVM耦合的日径流预测模型，以提高径流预测精度。与经典小波分析相比，EMD方法具有更好的抗噪能力，并已成功应用于非线性数据的处理分析中[12，14]。

综上所述，本文将对我国南方榕江流域日径流序列进行自相关分析，以及采用EMD方法对该数据进行适当分解，在决定输入步长的同时确定预测模型的输入数据，使用EMD-SVM模型对控制流域日径流预测，并设立LSTM、SVM、BP模型作为对照模型，以验证所建模型的预测性能。

1 研究方法

1.1 自相关分析

对于时间序列，自相关函数[15]主要用于分析该序列和其本身k阶滞时后的时间序列之间的相关程度，衡量历史序列对n时刻的影响。在径流数据中，自相关分析常用于研究时间序列自身随滞时增加而变化的周期性特征及检验径流序列自身相依性，同时可根据自相关程度判断模型输入数据和预测数据的关联性。

自相关系数公式为

式中，k为滞时(时移)步长，k=0，1，2，…，n；cov(Xt，Xt+k)为Xt和Xt+k的协方差；σXt、σXt+k分别为Xt和Xt+k的均方差。

因为水文序列具有波动性，在径流数据自相关分析中可选择显著性水平α，设置容许限。取α=5%，容许限水平为1-α=95%，公式为

式中，取负号为下限，取正号为上限，位于容许限外认为该序列具有相关性，反之该序列独立。

1.2 经验模态分解

经验模态分解(EMD)是由Huang于1998年提出的一种新型自适应处理非平稳信号的方法，不同于小波分解法与傅里叶变换法，EMD方法在理论上可以适用将任何一种类型的时间序列(信号)分解成不同时间尺度的时间序列(信号)分量，因而在对径流时间序列这种非线性数据的处理上，效果显著优于传统时频处理方法。EMD能够将复杂的信号根据其自身时间尺度特征分解成为有限个本征模函数(IMF)和一个残差r(t)，其中每个IMF都含有原始时间序列中不同尺度的局部特征信号，r(t)残差所表现的多为原始序列的整体趋势。分解得到的IMF需要满足以下两个约束：

(1)在整个数据集中，IMF含有的极值点数与零点数必须相等或最多相差1。

(2)在任何一点上，由局部最小值形成的下包络线和由局部最大值形成的上包络线的平均值应等于0。

对径流时间序列进行EMD分解分为以下步骤：

(1)根据原始径流时间序列信号x(t)确定上下极值点，分别画出下包络线amin(t)、上包络线amax(t)。

(2)求出下包络线amin(t)、上包络线amax(t)的均值，得到径流时间序列均值包络线m1(t)。公式为

(3)原始径流时间序列信号x(t)减去均值包络线m1(t)，得到去除低频信号的新时间序列信号h1(t)。公式为

h1(t)=x(t)-m1(t)

(4)

(4)判断该h1(t)是否满足IMF的上述两个约束，若不满足，则以h1(t)为基础，重做上述(1)～(3)的分析直至满足约束；如果满足，记c1(t)=h1(t)，该信号c1(t)作为第一个IMF分量，并将原始径流时间序列信号x(t)减去c1(t)，得到一个去除高频信号的残余分量r1(t)作为新的径流时间序列信号。公式为

r1(t)=x(t)-c1(t)

(5)

(5)重复上述步骤，得到x(t)的第n个IMF分量cn(t)，当残余分量rn(t)满足EMD分解终止条件(通常至rn(t)成为一个单调函数)，循环结束。

最终可以分解为n个IMF分量和一个残差rn(t)。公式为

(6)

1.3 支持向量机

支持向量机(SVM)是一种根据预选的非线性映射，把输入向量投映至某一个高纬度的特征空间，并通过最优用于分类的超平面的分类过程。SVM通过统计学习理论的VC维理论和结构风险最小化原理建立，其构架形式与多层感知器网络相似。

设有n个训练样本集合：{(xi，yi)}，i=1，2，…，n，其中xi为输入向量的元素，yi为预测向量的元素。SVM在高纬特征空间的线性回归函数为

f(x)=ωφ(x)+b

(7)

式中，ω为超平面法向量；φ(x)为非线性函数；b为超平面偏置项。

使用惩罚因子C和松弛变量ζ、ζ*，求解ω和b的凸二次规划，得到回归函数

(8)

式中，αi、αi*为二次规划Lagrange乘子；K(·)为任意满足Mercer条件的核函数。

SVM模型结构示意如图1。核函数K(·)将两个低维空间的向量，计算经某一变换后在高维空间的向量内积值，是构建SVM的关键成分。

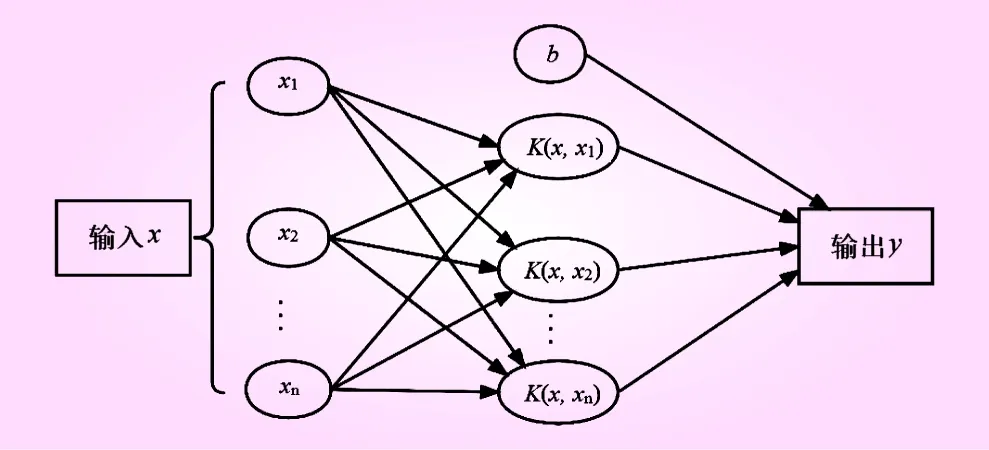
图1 SVM结构示意

1.4 EMD-SVM模型构建

EMD-SVM模型构建步骤如下，其模型构建的技术路线如图2所示。

图2 技术路线

步骤1。为提高SVM预测精度，使用自相关分析对日径流时间序列进行预处理，通过自相关系数大小确定模型的输入步长。

步骤2。利用EMD算法将日径流时间序列分解为不同时间尺度的IMF分量和一个残差r(t)。

步骤3。将径流时间序列数据按3∶1划分训练集和测试集，通过试错法寻找SVM最优惩罚因子C。

步骤4。滤除残差r(t)，将各个IMF的预测结果相加求和作为EMD-SVM模型最终预测结果。

1.5 评价指标

本文选取平均绝对百分比误差(MAPE)、均方根误差(RMSE)、纳什效率系数(NSE)3项指标评价模型性能。各计算公式为

(9)

(10)

(11)

MAPE值越接近0，表明模型误差越小；RMSE表示预测值与观测值的偏差，其值越小表明偏差越小，预测效果越好；NSE反映水文过程的拟合效果，取值范围(-∞，1]，当值越接近1，表明水文过程拟合效果越好，可以更加直观了解模型预测结果的精度和可靠性。

2 研究实例

榕江属于南海水系，是广东粤东地区第二大河流，也是连接香港与广州的重要航运通道。榕江流域河段总长度176 km，自西向东流经汕尾市、揭阳市、汕头市3市。其中南河为榕江流域主流，上游部分河道纵比降较大，由于榕江流域暴雨多，洪水传播迅速，易发生旱涝灾害。因此，高精度的径流预报对榕江流域及时发布预警，合理调控水资源发挥重要作用。榕江流域DEM数据图如图3所示。

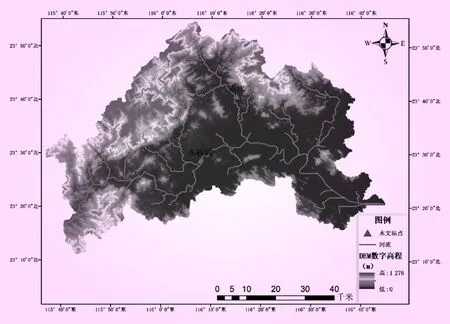
图3 榕江流域DEM

本文以榕江流域南河的东桥园站为研究对象。东桥园站集水面积2 016 km2，多年平均年径流31.1亿m3；搜集选取东桥园水文站2006年1月1日～2011年3月29日的逐日历史径流数据作为EMD-SVM日径流预测模型的训练期进行测试，2011年3月30日～2012年12月31日的逐日历史径流数据作为预测模型的检验期。

3 结果与讨论

3.1 日径流数据自相关分析

合理选择预测因子直接影响模型的预测精度，选择东桥园站日径流序列作为模型主要输入，日径流数据的自相关系数和容许限如图4所示。从图4中可知，当滞时k为3和9时，自相关系数位于容许限内，视为与历史数据没有相关性；当k为1和6时，自相关系数在容许限外且数值最大，但较长的滞时通过EMD分解，能使预测模型更好的学习径流时间序列内部规律，提高预测性能。因此，可认为当输入步长为6时，对预测精度的影响最大。

图4 东桥园站日径流自相关分析

3.2 EMD分解日径流数据结果

东桥园站日径流序列分解结果如图5所示。原始序列通过EMD分解，当重构EMD迭代次数设定为10时，得到10个IMF分量和1个残余函数r(t)。由图5可以发现，各IMF的频率由高到低递减，IMF1至IMF6的波动幅度较大，反映了原始径流量在不同情况下的变化趋势；IMF7至IMF10波形较为平缓，反映了原始径流量的随机性，各个分量的值较平均分布于零的两侧，EMD分解较为直观地显示了对日径流序列扰动较低的原始序列特征，故模型通过这些分量可以更精准地学习径流序列的规律性特征，之后进行预测，预测误差会减小。

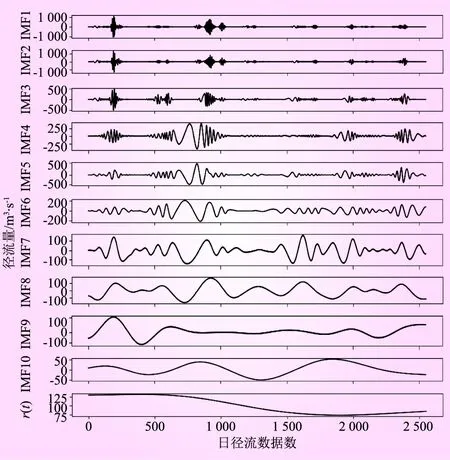
图5 东桥园日径流EMD分解

对EMD分解后得到的各个IMF序列建立各自SVM预测模型。使用子预测模型对各个子序列进行预测，并将径流预测值相加求和，获得最终预测结果。

3.3 SVM模型参数设置

SVM模型的惩罚因子C用来衡量目标函数损失的权重，当选取惩罚因子越大，表明对于错误样的惩罚程度越大，但存在过拟合的现象，降低模型泛化能力。故选取C(100、 200、 300、400、500、600、700、800、900、1 000、1 100、1 200)进行试验，选用预测结果最好的一组超参数。本文为了获得更佳的预测结果，选择多项式核(Polynomial kernal)作为SVM核函数，以未经EMD处理的测试集作为输入数据，不同惩罚因子C的测试结果如表1所示。

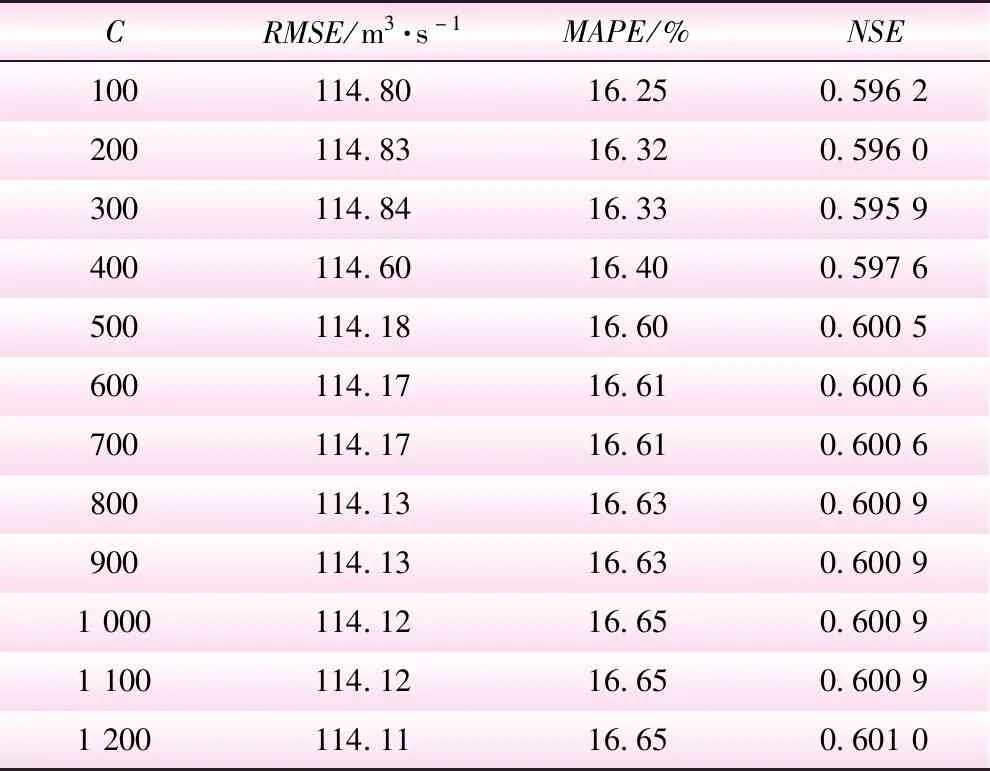
表1 不同惩罚因子C的测试结果

由表1可知，惩罚因子C在100～800范围内，对预测结果的影响较大；在800～1 200范围内，3项评价指标几乎不变，但模型运行时间有所增长。因此，当惩罚因子C选取800时，SVM模型具有较好的综合表现效果。

对各个IMF分量建立SVM模型，核函数kernel选择poly函数，多项式poly核函数的维度degree为3，核函数系数gamma选择auto。

3.4 模型预测效果

EMD-SVM模型的预测结果如图6所示，然后将EMD-SVM模型的预测结果与SVM、LSTM、BP模型的预测结果进行横向对比，如图7～9所示，以此验证该组合模型预测结果的精度与可靠性，SVM模型采用与EMD-SVM模型相同的参数及变量设置。

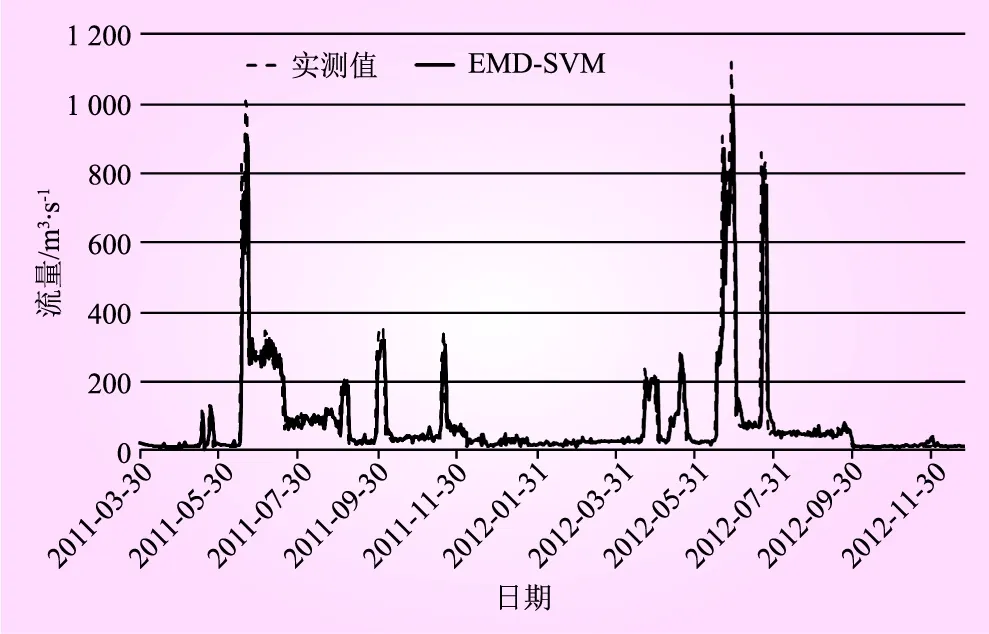
图6 EMD-SVM模型预测值与实际值对比

图7 SVM模型预测值与实际值对比

图9 LSTM模型预测值与实际值对比

为了直观地比较SVM预测模型结合EMD算法所得径流量预测结果的精度，显然，通过图6～9可知，在大流量的时间序列预测上神经网络的BP模型误差明显较大且数值偏小，LSTM模型预测浮动范围大，会出现预测值远大于实际值的现象，SVM模型存在和BP同样的问题；在中小流量的时间序列预测上SVM模型比LSTM、BP模型具有更高的预测精度。通过图6与图7、8、9对比，显然使用EMD算法对径流时间序列预先分解再分别进行预测，得到的结果更加接近真实值。

EMD算法较好地弥补了SVM模型在大流量预测上的不足，实现了大中小流量较高精度的预测，明显地提升了预测效果。各模型训练期与检验期的3项误差指标对比如表2所示。

表2 东桥园水文站日径流预测结果对比

由表2可以得出以下结论：

(1)在训练期，BP模型在RMSE和NSE指标上优于EMD_SVM模型，明显优于LSTM、SVM模型，但在MAPE指标上效果略劣于其他模型。在检验期，BP模型在RMSE、MAPE指标上高于其他模型，NSE指标低于其他模型，BP的预测性能大幅下降。

(2)预测模型在检验期可以更好地表现其真实性能。RMSE指标方面，EMD-SVM模型比SVM、BP、LSTM模型分别降低了19.60%、31.90%、29.66%；NSE指标方面，EMD-SVM模型比SVM、BP、LSTM模型分别提高了10.62%、24.50%、21.82%；MAPE指标方面，EMD-SVM模型比SVM、BP、LSTM模型分别减小0.024 8、0.082 5、0.001 7。因此，说明EMD-SVM模型的预测结果在检验期具有更高的精度，更加适用于研究区域的径流预测。

(3)通过大量数据对预测模型进行训练，相对于其他3个模型，LSTM神经网络模型在训练期和检验期的模拟效果均不突出。

(4)由于径流序列具有非平稳性和非线性性，且序列中多含有噪声的特征，使用SVM模型直接进行预测会降低对径流量的拟合效果。EMD分解可以对原始时间序列数据进行自适应分解，较为有效地提高了模型预测的精度。