基于机器学习和数值模拟的锅炉水冷壁热流密度分布预测模型

董凌霄，梁永，杨家辉，靳晓灵，杜勇博，邓磊，车得福

(西安交通大学 能源与动力工程学院，陕西 西安，710049)

煤炭在我国一次能源供应体系中具有重要地位，燃煤发电也在我国的电源结构中占据着主导地位[1]。“碳达峰、碳中和”目标的提出加速了我国经济和能源结构的转型[2-3]。尽管可再生能源持续强劲增长，风能与太阳能装机容量持续增加，但燃煤机组在以新能源发展为主体的新型电力系统下的作用非常重要。为适应风力和太阳能发电等新型发电系统的波动性，火力发电在电网调峰中的作用将更加明显，这对燃煤机组变负荷运行能力提出了更高要求。炉内工作过程由燃烧和炉内传热组成，炉内传热不仅直接影响炉膛温度，还决定着离开炉膛进入对流受热面的能量[4]。为保障锅炉在变负荷运行下的安全性，确保受热面尤其是水冷壁处在合理的耐温极限内是关键。

水冷壁热流密度与锅炉输入热量和炉内燃烧情况密切相关。水冷壁局部热流密度可用来计算工质参数沿程变化，校验水循环动力和水冷壁壁温[5-7]，其分布规律也是研究炉膛内换热的重要指标。水冷壁热流密度分布可通过实验测量[8]、经验总结[9]和数值模拟[10-11]等途径获取。马达夫等[12]使用热电偶测量了某600 MW 超临界W 火焰锅炉水冷壁向火面和背火面的壁面温度，并使用背火面温度代替工质温度，基于传热学原理计算了水冷壁热流密度分布。炉内的恶劣环境会导致测点布置和仪表安装存在困难，并且温度测量的精度和可靠性也难以保证，这限制了实验测量方法的应用。一些水动力计算标准给出了炉内热流密度的经验分布，然而适用范围有限。ZHANG等[13-15]利用数值模拟手段，分别针对600 MW超临界拱形燃烧锅炉、600 MW四角切圆煤粉锅炉和超临界二氧化碳锅炉获得了较全面的水冷壁热流密度分布。与实验测量和经验总结相比，数值模拟具有技术成熟、成本低和数据完备等优点，但模拟过程复杂、耗时长，该缺点同样限制了该方法的直接应用。值得注意的是，机器学习算法在燃煤电厂建模中得到了广泛应用。以往的研究主要将机器学习应用在NOx排放预测[16]、水冷壁积灰结渣在线监测[17-18]、锅炉效率优化[19]等方面，预测水冷壁热流密度分布的研究尚未见报道。将机器学习和数值模拟方法相结合，为快速、准确预测水冷壁热流密度分布提供了新思路。

本文首先通过数值模拟计算某660 MW超临界直流锅炉在48 种工况下的水冷壁热流密度分布，为机器学习提供原始样本数据；其次，通过皮尔逊相关分析和紧邻成分分析确定特征子集，利用贝叶斯优化结合交叉验证的方法优化支持向量机、决策树和提升树算法模型；最后，基于优选的算法模型，建立最终的水冷壁热流密度分布预测模型。

1 锅炉水冷壁热流密度模拟计算

1.1 锅炉结构

图1所示为某600 MW 超临界直流锅炉结构及燃烧器布置示意图。该炉膛宽度和深度分别为18 816 mm 和17 696 mm，水冷壁下集箱标高为8 300 mm，炉顶管中心标高为72 350 mm，炉底冷灰斗角度为55o。在炉膛冷灰斗进口到炉膛标高49 720 mm 处采用倾角为13.95°的螺旋管圈布置，螺旋管圈上部采用垂直管圈均匀布置在锅炉四面墙上，螺旋式水冷壁和垂直上升式水冷壁之间采用混合集箱进行连接转换。沿着烟气流动方向依次布置着6片分隔屏过热器、20片后屏过热器、末级再热器和末级过热器。喷嘴由煤粉喷嘴(A-F)、二次风喷嘴(UFA、AUX 和CCOFA)和燃尽风喷嘴(SOFA)组成，以四角切圆方式组织煤粉的燃烧。锅炉变负荷运行时，给煤量、燃烧器投运层数和过量空气系数等运行参数都随之变化，数值模拟中采用的运行参数如表1所示。

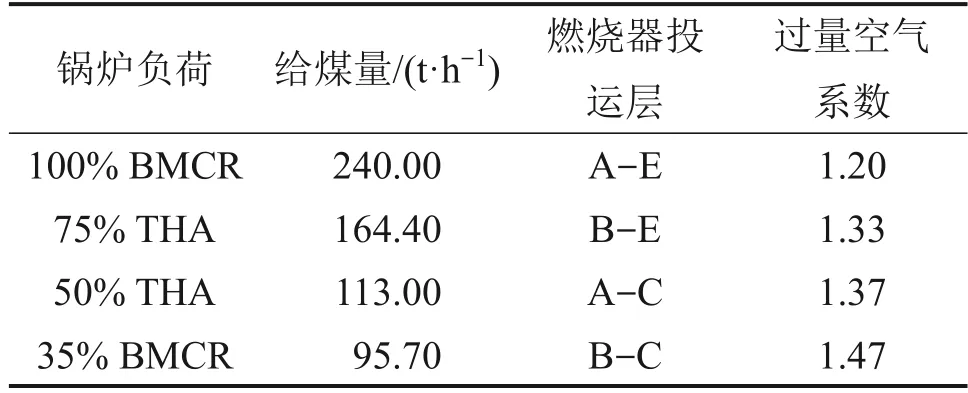
表1 不同负荷下的运行参数Table 1 Operating parameters under different loads

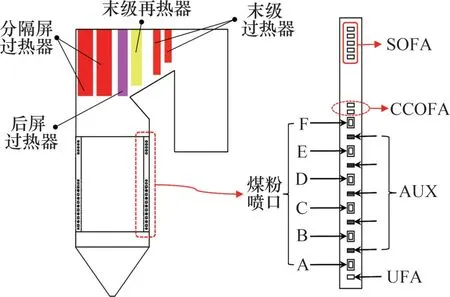
图1 某600 MW锅炉结构及燃烧器布置示意图Fig.1 Boiler structure and burners arrangement of 600 MW

1.2 水冷壁热流密度分布计算

1.2.1 网格划分与边界条件

采用ICEM中的六面体结构化网格对该直流锅炉进行网格划分。计算区域由冷灰斗底部至锅炉后烟井。在冷灰斗区域，由于炉内参数变化不大，网格设置较稀疏。在燃烧器区域，由于燃烧反应剧烈、温度等物理量变化较快，对该区域进行网格加密。采用标准κ-ε模型对湍流流动进行计算[20]；采用双步竞争反应模型描述挥发分[21]，焦炭燃烧采用扩散/动力模型[22]进行分析；煤粉颗粒在炉内的燃烧和流动过程采用随机轨道模型进行分析[23]；采用离散坐标辐射模型计算辐射换热过程。在本研究中，燃烧器及燃尽风入口均为质量流量入口，一次风和二次风入口质量流量分别为128.86 kg/s 和354.38 kg/s，一次风和二次风的温度分别为353 K 和612 K。在模拟过程中，过量空气系数为1.20，炉膛壁面条件选用定壁温边界条件，壁面温度取水冷壁入口工质温度和出口工质温度的平均值，即670 K。该600 MW 超临界直流锅炉的设计煤种为神府东胜煤，本文共模拟了3个实验煤种用于后续特征选择及预测模型，详细煤质参数如表2所示。

表2 实验煤种煤质参数Table 2 Fuel properties of bituminous coal

1.2.2 模型验证

本文选用了网格数为1 337 476、1 752 193、2 067 250 和2 478 099 个这4 种网格进行网格无关性检验。由4种网格计算得到的炉膛截面平均温度沿炉高方向变化趋势基本一致，当网格数量从1 337 476 个增加到2 067 250 个时，计算结果存在较大幅度的变化，但当网格数量从2 067 250 个增加到2 478 099 个时，计算结果基本不变，这说明当网格数量为2 067 250 个时，可获得网格独立的解。考虑到计算时间与计算精度，最终选择2 067 250个的网格进行计算。

该锅炉的蒸汽侧温度热力计算结果与实际监测结果的相对误差很小，说明计算得到的受热面出口烟气温度和吸热量与运行结果接近，可作为验证数值模拟可靠性的参考。屏底烟温和末过(热段)进口烟温的数值模拟与热力计算结果对比见表3。从表3可以看出，在100%的BMCR负荷下，计算结果偏差最大为2.92%；除此之外，水冷壁吸热量在100%的BMCR 负荷工况下模拟值为659.33 MW，热力计算结果为609.86 MW，相对误差为8.11%。从表3还可见：低负荷的末过(热段)进口烟温最大相对误差在8%左右，高负荷以及低负荷下屏底烟温相对误差均在5%以内。根据以往的研究，认为该计算模型是可靠的[24-27]。

表3 屏底烟温和末过(热段)进口烟温的数值模拟与热力计算结果对比Table 3 Comparison between numerical calculation and thermal calculation for smoke temperature at screen and final superheater inletK

1.3 样本建模与数据选取

在“双碳”目标和以新能源发展为主体的新型电力系统下，由于新能源的波动性，燃煤机组需要频繁参与电网负荷深度调峰，锅炉变负荷运行已成为常态。当锅炉负荷变化时，炉内温度发生变化，进而影响水冷壁热流密度的分布。不同煤种之间灰分、水分、挥发分等煤质参数差别较大，同一锅炉燃用不同煤种时燃料燃烧特性也会不同。增加煤中水分和灰分含量或者降低挥发分和热值均会导致煤粉的着火时间推迟，火焰拖长且火焰中心上移，从而引起水冷壁热流密度变化。锅炉采用的空气分级燃烧等低NOx技术也会影响水冷壁的热流密度分布。

综上所述，影响水冷壁热流密度的因素主要包括锅炉负荷、燃料特性及运行方式3个方面。运行方式参数包含一次风率、燃烧器摆动角度、SOFA摆动角度、主燃区过量空气系数、风温、风速等。通过数值模拟，为机器学习预测模型提供原始的样本数据集。设计数值模拟的工况，共计48组工况，部分数值模拟工况见表4。

表4 部分数值模拟工况Table 4 Part of numerical simulation conditions

2 机器学习预测模型

2.1 特征选择

机器学习模型预测性能的上限由数据质量决定。在数据采集完成后，详细分析数据，进一步选择与提取特征，从而找到对响应变量影响最大的特征。在采集完成由48 组工况模拟结果组成的数据集后，需对数据进行相关性及近邻成分分析，最终确定预测模型的输入变量。

皮尔逊相关系数用于衡量2个变量间线性相关性，其值介于-1～1 之间。当2 个变量之间的皮尔逊相关系数大于0.4时，认为变量之间具有中度或强相关性[28]。皮尔逊相关系数r的计算公式如下：

式中：n为样本数量；Xi为变量X的第i个观测值；-X为变量X的样本平均数；Yi为变量Y的第i个观测值；-Y为变量Y的样本平均数。

皮尔逊相关分析结果如表5所示。从表5 可见：锅炉负荷、给煤量、总风量、一次风量、二次风量、二次风温、二次风速以及前墙水冷壁网格单元几何中心纵坐标y等参数与该锅炉前墙的壁面热流密度分布具有很强的相关性，但煤质参数、SOFA风量、燃烧器摆动角度、SOFA风摆动角度、一次风速、SOFA风速和前墙水冷壁网格单元几何中心横坐标z等参数与锅炉前墙壁面的热流密度的相关性不大，这与前人的研究结果[29-30]存在一定的矛盾。由于锅炉燃烧系统具有多变量、非线性以及强耦合等特点，需要进一步选择特征。

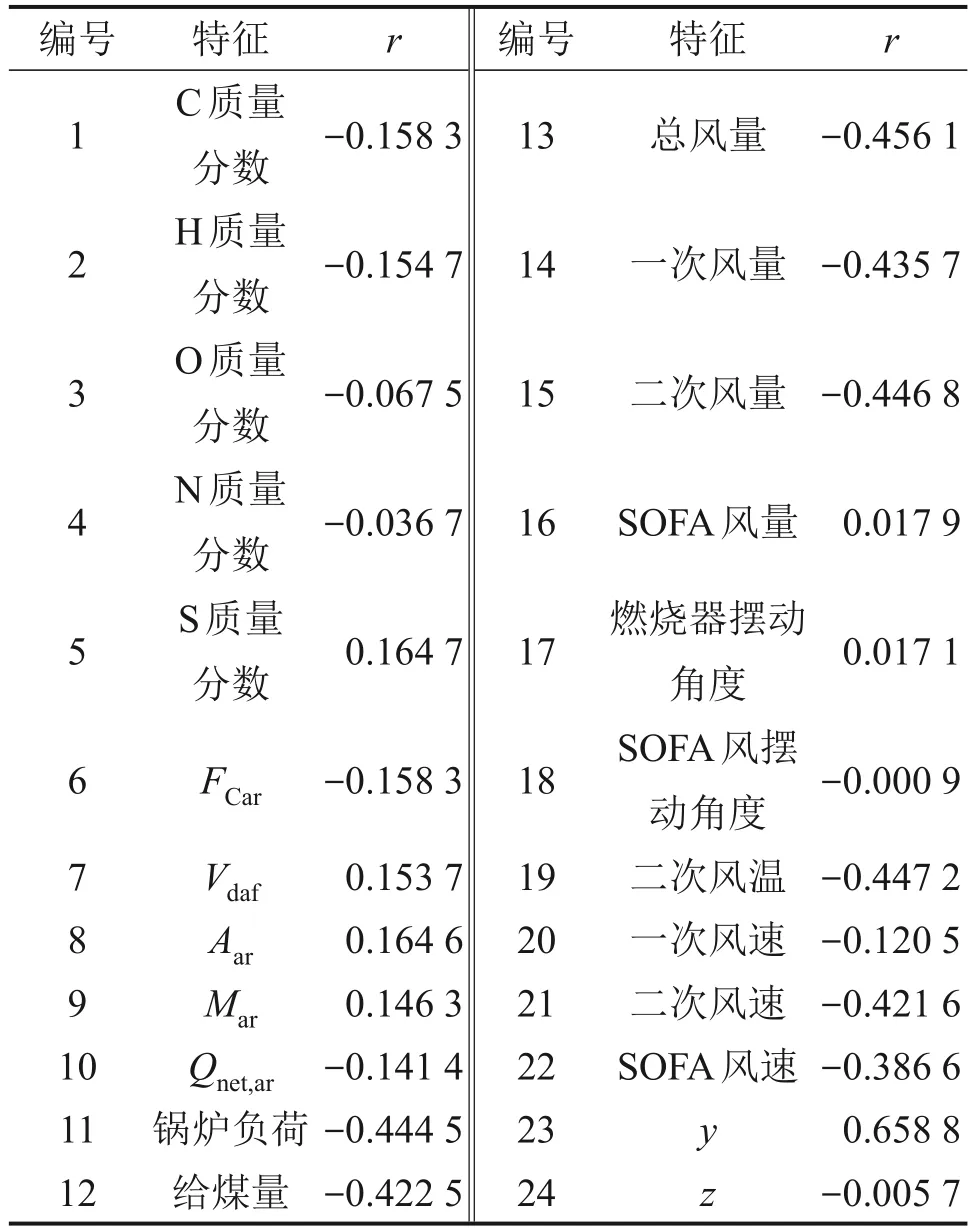
表5 各个特征的皮尔逊分析结果Table 5 Results of Pearson's analysis for each sign

在皮尔逊相关分析的基础上，利用近邻成分分析算法进一步选择特征。近邻成分分析方法可以最大程度地提高回归和分类算法的预测准确性。近邻成分分析特征选择的结果如图2所示(其中，特征编号见表5)，编号为1(C 质量分数)、12(给煤量)、13(总风量)、15(二次风量)、17(燃烧器摆动角度)、18(SOFA 风摆动角度)、23(水冷壁网格几何中心坐标y)、24(水冷壁网格几何中心坐标z)可作为特征选择的结果。

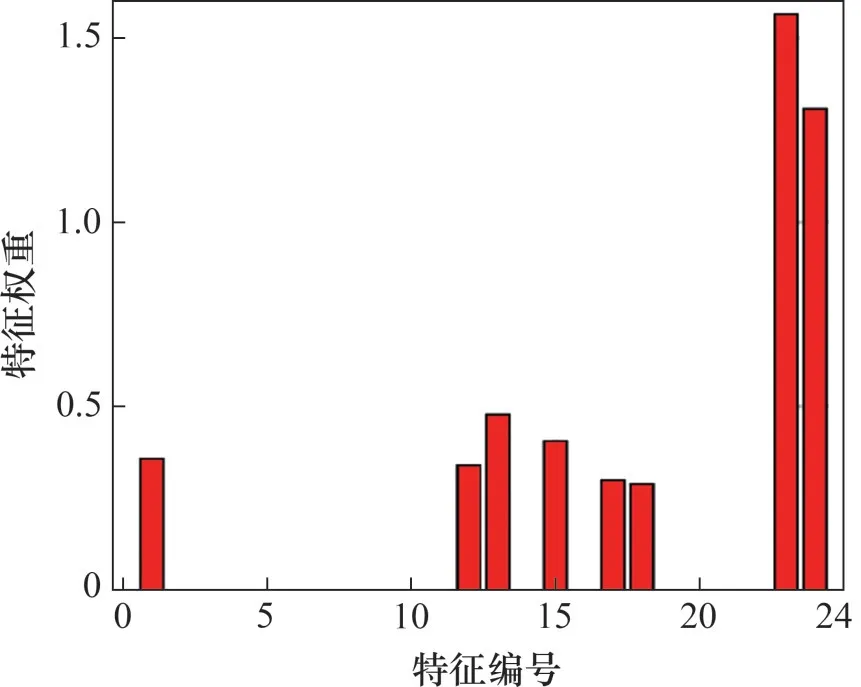
图2 近邻成分分析的结果Fig.2 Results of neighborhood component analysis

全面考虑煤质参数、机组负荷、配风情况以及网格单元几何中心坐标等关键因素，结合模型复杂度和精准度，取2种方法得到的特征子集的并集为预测模型的输入变量。由于锅炉负荷和给煤量这2个特征之间并不相互独立，删除锅炉负荷这个冗杂的特征，最终确定共11 个特征作为水冷壁热流密度预测模型的输入变量，包括C、给煤量、总风量、一次风量、二次风量、二次风温、燃烧器摆动角度、SOFA风摆动角度、二次风速以及水冷壁网格单元几何中心坐标y和z。

2.2 3种算法模型的建立和评估

利用MATLAB 自带的randperm 函数，生成伪随机数，并划分数据集，rng 设置为42。在9 600个样本中，选择85%的样本作为训练集，剩余的15%样本作为测试集。在使用算法构建模型之前，需要对数据进行归一化预处理，使样本每个特征值都映射到[-1，1]之间，不仅可加快计算时的预处理速度，还可以防止属性值数量级较小的特征被淹没，造成原始数据信息丢失。

式中：xscale、xmax、xmin和分别为属性x归一化后的数值、最大值、最小值和均值。

采用贝叶斯优化算法并结合五折交叉验证，对支持向量机、决策树、提升树进行超参数优化。在优化过程中，三者超参数选择不同，迭代次数均设置为30 次。支持向量机优化时，超参数为“框约束”和“核尺度”，这2 个参数分别以一定的函数关系对应支持向量机算法的惩罚系数C和核系数g，搜索范围均为0.001～1 000，优化结果如下：框约束为19.53，核尺度为0.80。决策树模型优化时超参数为“最小叶”，超参数搜索范围为1～4 080，最终最小叶优化结果为1。提升树优化时超参数选择最小叶、学习器数量和学习率，搜索范围分别为1～4 080，10～500和0.001～1，优化结果如下：最小叶为113，学习器数量为448个，学习率为0.31。

图3 和图4所示分别为3 种算法模型在训练集和测试集上的预测效果。从图3 和4 可以看出：3种方法模型在训练集上的预测值与模拟值相对误差较小，测试集上的预测值与目标值也非常接近，与数值模拟的结果吻合程度较高，且没有出现过拟合现象。3 种模型的预测性能(均方根误差、均方误差和决定系数)如表6所示，支持向量机模型、决策树模型和提升树模型的R2依次为0.983 6、0.970 7和0.985 0，均比较接近1。因此，利用支持向量机、决策树和提升树建立的3种预测模型均具有较高的预测精度和较强的泛化能力，3种算法建立的水冷壁热流密度预测模型是可行和可靠的。

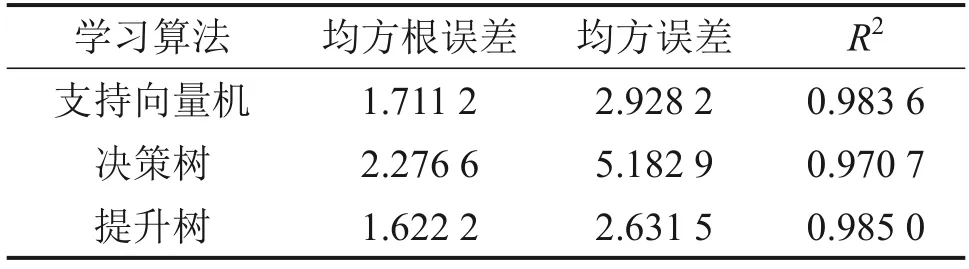
表6 不同学习算法的预测性能Table 6 Predictive performance of different learning algorithms

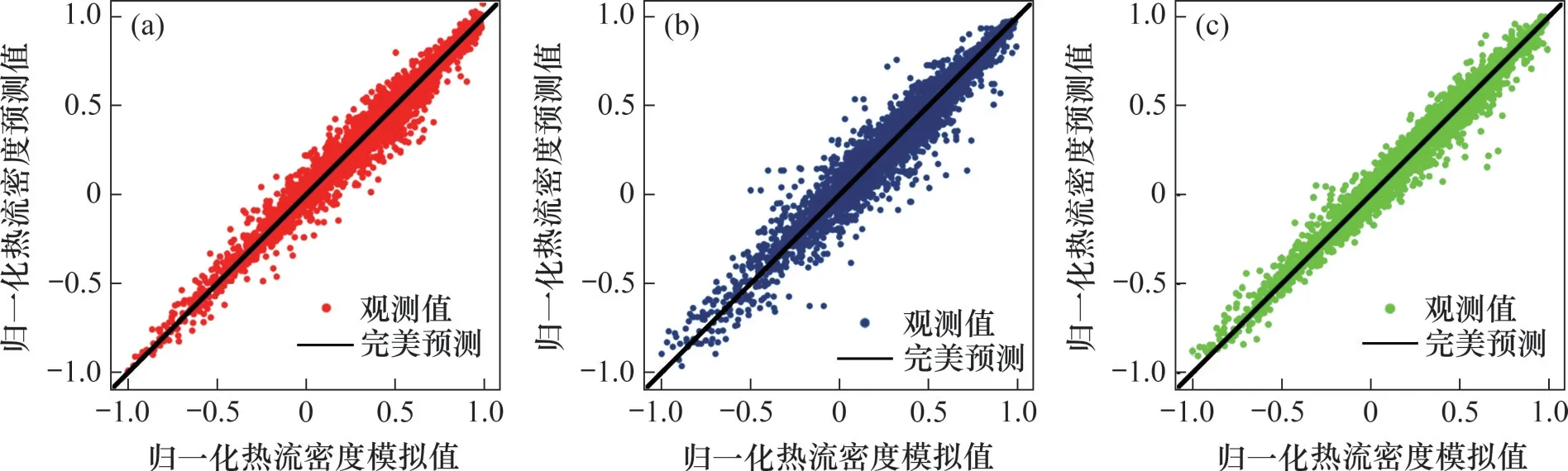
图3 不同算法预测模型在训练集上的预测效果Fig.3 Prediction of different algorithm prediction models on training set

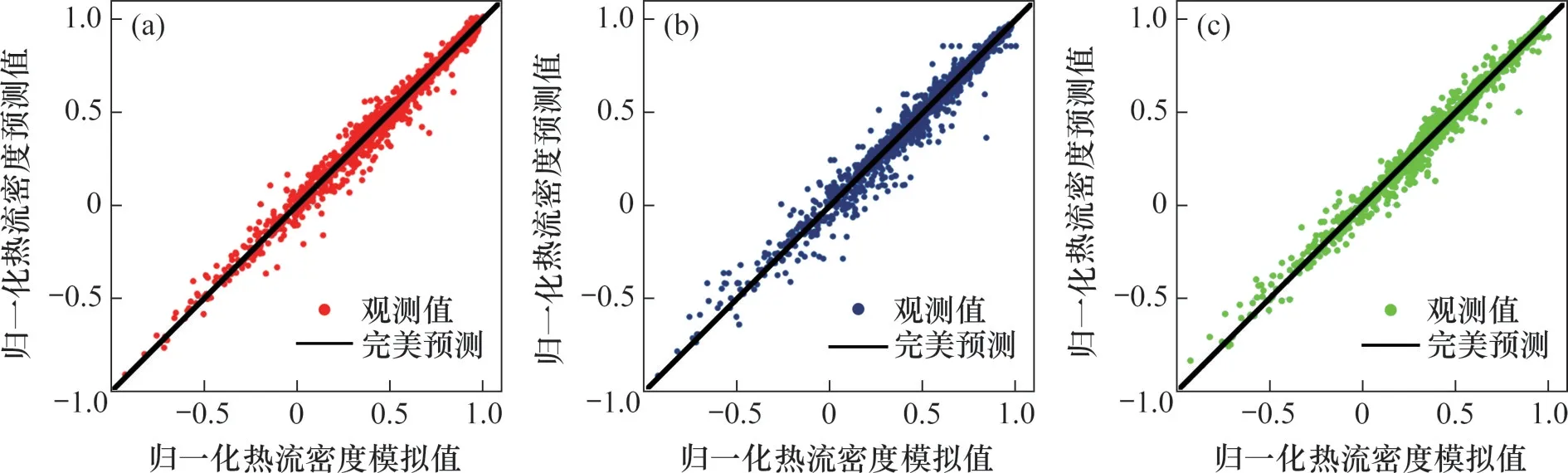
图4 不同算法预测模型在测试集上的预测效果Fig.4 Prediction of different algorithm prediction models on test set

从预测性能来看，提升树算法建立的模型具有更高的预测准确性，但与支持向量机算法构建的模型相比并没有明显差距。支持向量机是基于小样本统计学习理论建立的，具有不受限于样本总量的特点，被认为是针对小样本条件下分类和回归的最佳学习方法。锅炉水冷壁热流密度的模拟计算存在计算量大、耗时多等问题，难以获得较大数量的样本数据。综合考虑样本容量和预测性能，可采用支持向量机预测锅炉水冷壁热流密度。

2.3 锅炉水冷壁热流密度分布预测模型的建立和评估

基于以上研究，利用LIBSVM 工具箱编写锅炉水冷壁热流密度预测软件，以方便用户利用支持向量机建立锅炉水冷壁预测模型。预测模型采用MATLAB R2020b 中的App Designer 作为开发工具，运用面向对象的程序设计技术编制。在设计技术编制过程中，还参考并引用了Faruto 版本的LIBSVM加强工具箱的部分辅助函数。归一化范围选择[-1，1]，超参数优化方法选择贝叶斯优化，惩罚系数C和核系数g的寻优范围均设置为[0，100]，交叉验证的折数为20，得到的最佳参数为C=99.21，g=0.000 49。采用最佳参数和训练集对模型进行训练，得到锅炉前墙壁面热流密度峰值预测模型。模型在训练集上的拟合效果如图5所示，其中，热流密度正值表示烟气将热量传递给水冷壁。

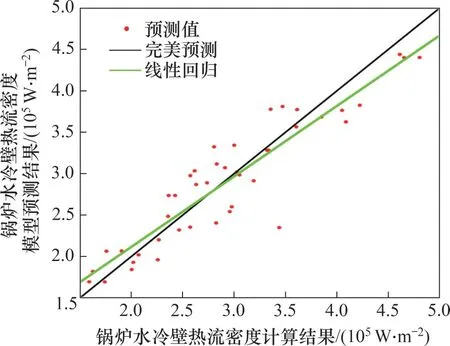
图5 预测模型在训练集上的锅炉水冷壁热流密度训练结果Fig.5 Results of predictive modeling on training set of heat flow density distribution in boiler water-cooled walls

图6所示为预测模型在训练集上的锅炉水冷壁热流密度训练结果。模型在训练集上的均方误差为0.039 2，R2为0.849 6，在测试集上的均方误差为0.007 7，R2为0.979 7。预测软件得到的结果具有较高的预测精度和较强的泛化能力，可以准确地预测锅炉的水冷壁热流密度。

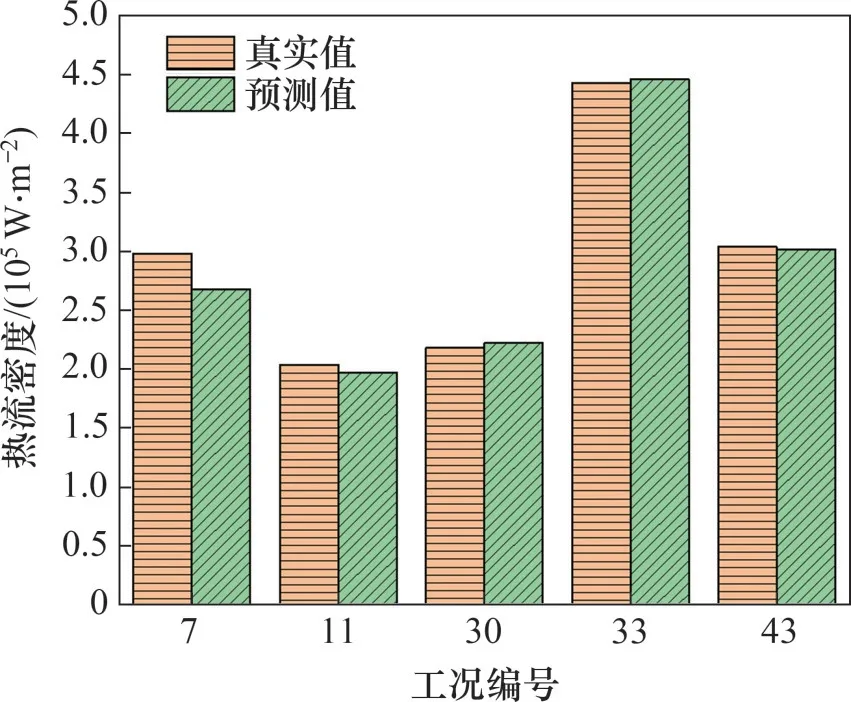
图6 预测模型在测试集上的锅炉水冷壁热流密度训练结果Fig.6 Results of predictive modeling on test set of heat flow density distribution in boiler water-cooled walls

3 结论

1)通过理论分析得到水冷壁热流密度的各个影响因素，设定样本建模数据的工况。在此基础上，通过皮尔逊相关性和近邻成分分析，选择C、给煤量、总风量、一次风量、二次风量、二次风温、燃烧器摆动角度、SOFA风摆动角度、二次风速以及水冷壁网格单元几何中心坐标y和z作为水冷壁热流密度分布预测模型的输入变量。

2)利用贝叶斯优化结合交叉验证的方法对支持向量机、决策树和提升树3 种算法进行超参数优化，三者所构建的水冷壁热流密度分布预测模型在测试集上的均方根误差分别为1.711 2、2.276 6 和1.622 2，R2分别为0.983 6、0.970 7 和0.985 0，均具有较高的预测准确性。经综合考虑，选择支持向量机算法构建水冷壁热流密度预测模型。

3)利用优化后的支持向量机算法建立的水冷壁热流密度分布预测模型，模型具有较高的预测精度和较强的泛化能力，可以对锅炉的水冷壁热流密度进行准确预测。