基于剪切波速的粗粒土填料压实密度控制理论
2023-10-30陈晓斌谢康尧俊凯王业顺唐禄博
陈晓斌,谢康,尧俊凯,王业顺,唐禄博
(1.中南大学 土木工程学院,湖南 长沙,410083;2.中南大学 教育部重载铁路工程结构重点实验室,湖南 长沙,410083;3.中国铁道科学研究院集团有限公司 铁道建筑研究所,北京 100081)
为了保证高铁路基的安全性以及提高列车运行的舒适性,相关规范对路基填料的压实质量均有着严格的要求[1-3]。路基压实质量的控制指标以压实系数K、地基系数K30等为主[4],其中,以压实系数进行路基压实质量控制的方式较为普遍,可以直接反映路基的实际压实效果。目前,测试路基填料压实密度的方法有环刀法和灌砂法等,且以灌砂法的应用最广泛[5]。灌砂法的原理简单,但测试数据离散性大,效率较低,且所挖的试坑也在一定程度上破坏路基本体[6]。因此,亟需提出一种更加快速、便捷、易于操作、无损的压实密度测试方法。
目前,剪切波速vs是表征细粒土强度、变形模量以及干密度等参数的重要方法[7-8],CHEN等[9-11]探讨了剪切波速与红黏土强度定量关系,建立了红黏土强度预测方程;张千里等[12]利用剪切波速理论,计算细粒土最大剪切模量,提出了砂土中的广义有效应力预测模型;张宇辉等[13]则引入体积膨胀率γv,建立了剪切波速与细粒土干密度评估模型;李建鑫[14揭示了影响路基填料压缩强度与剪切波速的主控因素,证明了剪切波速与路基填料压缩强度具有较强相关性;李少波等[15]针对含砂低液限黏土、含砂低液限粉土等细粒土试样,建立了黏土、粉土的干密度与剪切波速的关系模型。由此可见,针对细粒土采用剪切波速来表征压实密度的理论和测试体系较为成熟。然而,粗粒土填料属于多相介质,内部颗粒间的粒度及性质均有较大差异,仍采用细粒土的剪切波速与压实密度理论和测试方法,效果不理想[16]。
基于对于粗粒土的剪切波速研究的不足,深入探讨粗粒土压实密度与剪切波速的定量关系,旨在建立粗粒土填料剪切波速与压实密度理论方程,并通过试验验证理论方程适用性,同时,提出适用于粗粒土填料的剪切波速测试方法。研究成果可为快速测试粗粒土填料的压实密度提供新思路。
1 粗粒土剪切波速-压实密度理论方程
1.1 基于颗粒接触理论的粗粒土剪切模量研究
首先,基于弹性动力学理论推导出理想介质剪切波速方程[17]:
式中:vs为剪切波速;G为粗粒土剪切模量;ρ为粗粒土密度;E为粗粒土弹性模型;μ为粗粒土泊松比。在压实过程中,粗粒土的剪切模量、密度实时发生改变,而剪切模量的测试方法较复杂,导致无法准确建立粗粒土剪切模量、密度与剪切波速之间的定量关系。同时,剪切波波长处于10~30 cm范围内,对于细粒土而言,剪切波波长远大于土颗粒粒径,故近似将细粒土视为连续体,然而,粗粒土粒径较大,无法完全近似视为连续体。赵明阶等[18-19]研究砂土和土石混合料的剪切波速计算公式时,将土颗粒等效为粒径相等、材料性质相同的等球体,虽然等效的假设更合理,但无法量化不同粒径的粗细颗粒。故本文将粗粒土中颗粒分为粗颗粒和细颗粒2 种球形,如图1(a)所示。此时,颗粒间接触的类型主要2种:相同颗粒之间接触以及不同颗粒之间接触,分别如图1(b)和1(c)所示。
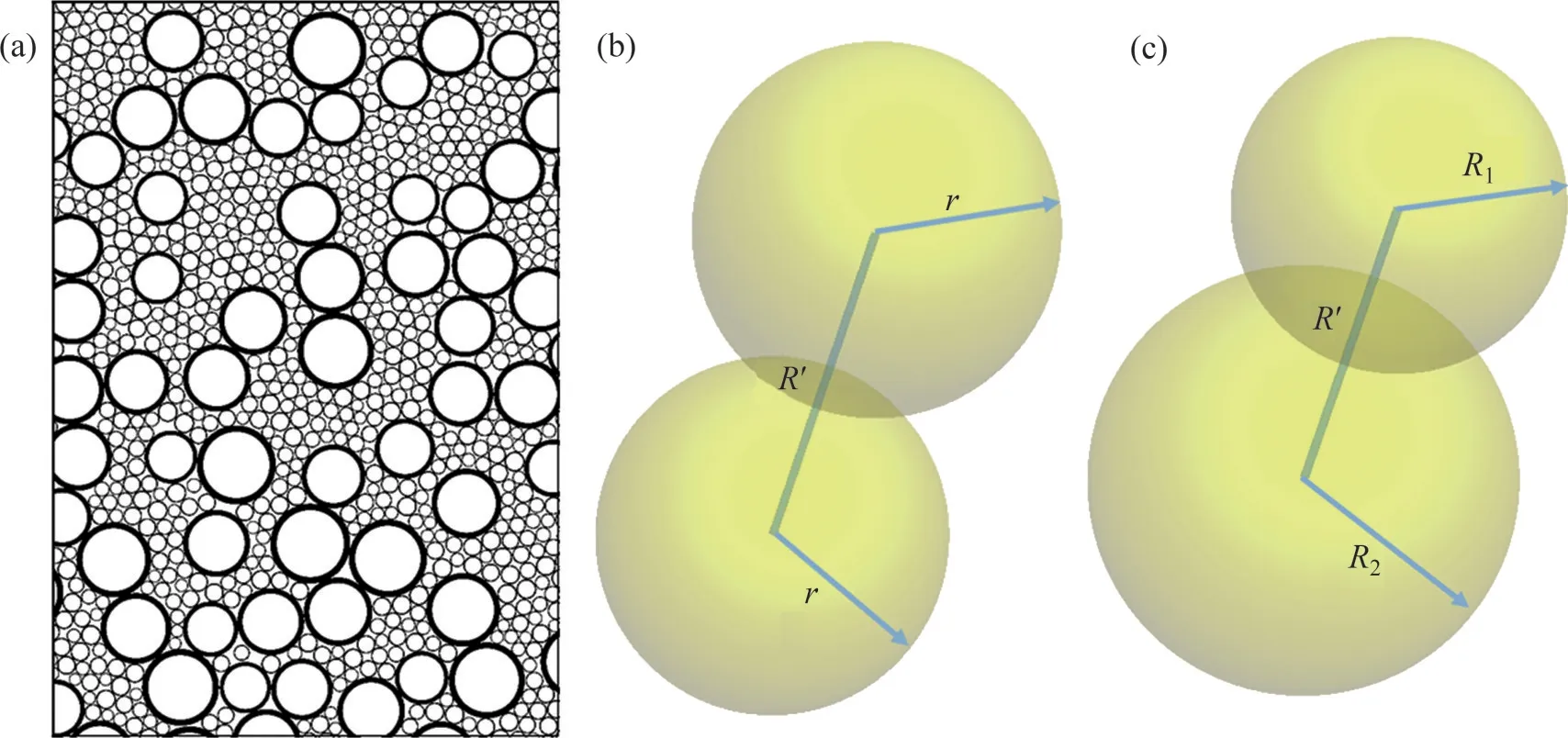
图1 粗粒土简化模型Fig.1 Simplified model of coarse-grained soil
基于钟晓雄等[20]提出剪切模量理论公式,可得相同颗粒接触时剪切模量G:
式中为粗粒土平均配位数;e为粗粒土孔隙比;r为颗粒半径;Dn和Ds分别为颗粒接触的法向刚度和切向刚度。
类似地,不同颗粒接触时剪切模量G:
以不同颗粒接触为例,推导散粒体剪切波速方程。首先,基于Hertz 接触模型[21],2 个球体受力挤压变形时,则球体间位移δ为:
式中:P为两球体间接触法向力;μ1和μ2分别为粗颗粒和细颗粒的泊松比;E1和E2分别为粗颗粒和细颗粒的弹性模量;k1和k2为球体间位移计算系数;δ为两球体间位移,即为图1(c)中R1+R2-R′。
因此,球体接触间的法向接触刚度Dn为
引入LI 等[22]所提出的刚度比概念,建立颗粒刚度与颗粒接触泊松定量关系:
式中:μ12为刚度比计算系数;kr为刚度比,即法向刚度与切向刚度的比。
综上可知,通过式(3)、(7)以及式(10),结合式(1)即可求得不同颗粒接触散粒体剪切波速方程。
类似地,相同颗粒散粒体剪切波速方程为:
基于所得粗粒土剪切波速计算公式,分析各参数对于剪切波速的影响关系,结果如图2所示。
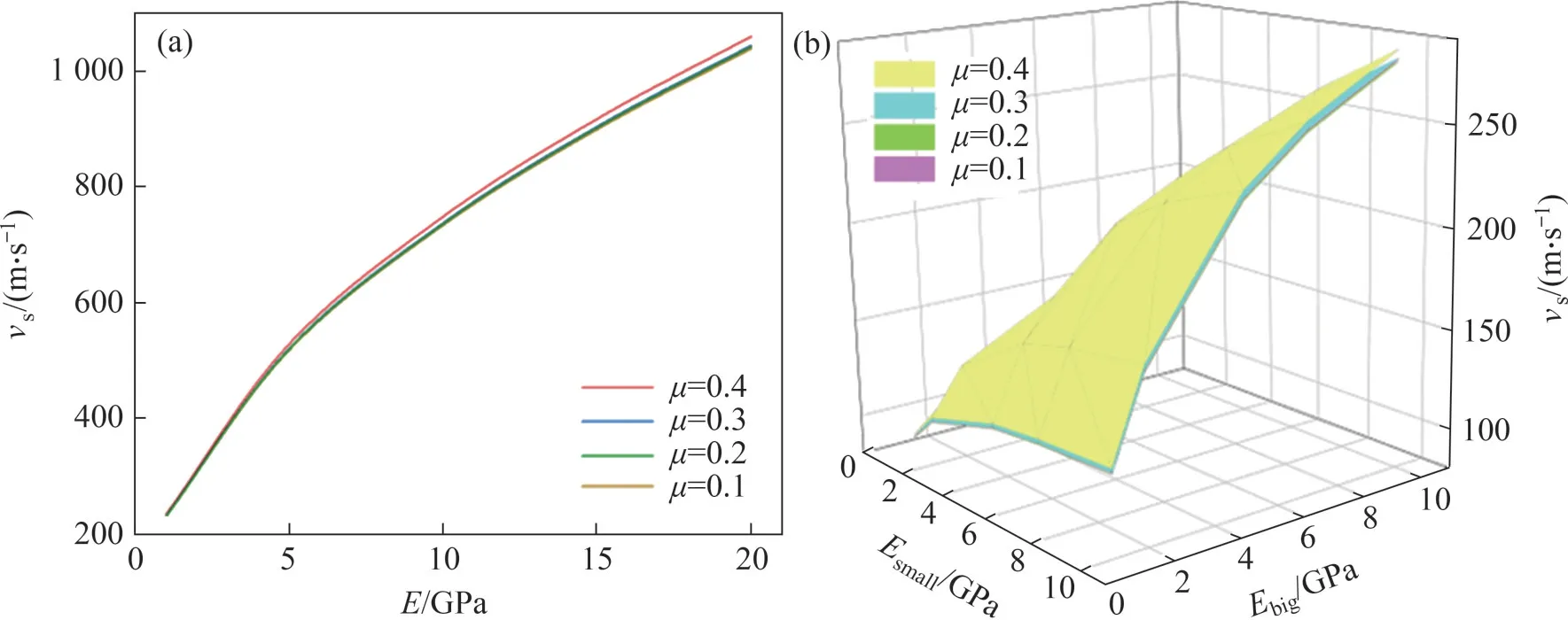
图2 剪切波速-压实密度理论的参数分析Fig.2 Parametric analysis of shear wave velocity-compaction density theory
从图2(a)可见:对于相同颗粒计算模型,颗粒的泊松比μ对剪切波速结果影响不大,而颗粒弹性模量对理论剪切波速的影响大,剪切波速随着颗粒弹性模量提高而增加。从图2(b)可见:对于不同颗粒计算模型,颗粒的泊松比μ对于剪切波速的影响不大,而颗粒弹性模量对剪切波速的影响更大,如当泊松比μ为0.2,弹性模量从5 GPa 增大到10 GPa时,剪切波速从197.9 m/s增大到279.9 m/s,提升了41.4%。
1.2 粗粒土干密度与剪切波速理论模型
在实际情况中,粗颗粒路基填料整体土体的颗粒接触形式并不是单一的,而是多种颗粒接触形式共存,且压实过程中填料颗粒参数一般(如单个颗粒粒径、刚度等)是固定的。根据1.1节的理论公式,不同接触形式的理论计算公式不同,剪切波在复杂级配的粗粒土中在不同部分以不同速度传播。
首先,按不同颗粒接触形式将剪切波传播路径按不同波速分段:
式中:v′1为相同颗粒接触部分的剪切波传播速度;v′2为不同颗粒接触部分的剪切波传播速度;s1为相同颗粒接触的剪切波传播距离;s2为不同颗粒接触的剪切波传播距离;s=s1+s2,为整体剪切波传播距离;t为整体剪切波传播时间;v′为整体表观剪切波传播速度。为方便计算,整体取倒数处理:
其中,不同剪切波速对应不同形式的颗粒接触,其剪切波速与土体颗粒性质间的关系为
基于杨尚惠等[23-24]的配位数计算理论,平均配位数计算如下:
式中:ϕ为孔隙率。
孔隙率与土体密度有如下关系:
式中:ρs为粗粒土的颗粒密度。
将式(16)~(19)代入式(15)。假定单个颗粒的密度均相同,按照级配即粗细颗粒质量比,等价得到粗细颗粒体积比,再根据颗粒的粒径比,推断出颗粒数量比,进而得到其配位数的关系,并将式(18)代入,可得:
式中:a、b和c为与所用填料级配相关的颗粒接触配位数系数。式(21)涉及参数较多,对实际使用造成了一定不便,但所涉及的参数M、ρs均只与土体性质相关,即当填料确定后,这些参数均保持不变,在同种土体的压实过程中不发生变化。
1.3 数值验证
采用Comsol 数值软件建立模型,进一步验证理论公式的正确性。建模时,使用与理论相同的假设条件,将粗粒土近似为无限空间,模型采用周期性边界来模拟这种无限空间土体中传播的剪切波,取直达波进行分析,避免边界折射、反射等现象的影响。
由于在Comsol 中采用周期性结构进行模拟,故建模时只需要建立最小单元,然后进行重复即可。图3所示为相同颗粒以及不同颗粒的数值计算模型图,分别对应于理论公式中相同颗粒组成的散粒体以及2种不同颗粒组成的散粒体模型。模型的剪切波速通过Comsol 软件内置的固体物理周期性结构计算方程求解。模型中,频率与波矢之间的频散关系为

图3 不同颗粒类型的数值计算模型Fig.3 Numerical computation model of different particle types
式中:ω为频率;k′为波矢。
对于模型的参数,按照表1进行取值。值得注意的是,模型及参数取值仅为了验证1.2节中粗粒土压实密度与剪切波速方程在假定和推导等理论方面的合理性,与实际粗粒土存在一定偏差。

表1 数值模型的参数取值Table 1 Numerical model parameter values
图4所示为理论模型与Comsol 数值模型对不同接触类型的剪切波速计算结果对比图。由图4可知:理论公式与数值模拟计算的剪切波速相近,预测趋势相同。由于数值模拟与理论模型的假设条件并不完全一致,例如理论模型在计算颗粒模量时近似认为各向同性,同时数值模拟与理论分析对于2 个球体间接触后体积的计算方法也不同。故理论计算和数值模拟间仍有一定的相对误差,但相对误差在8%以内,可认为理论模型是正确的。
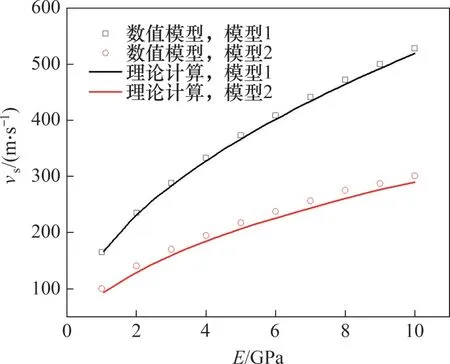
图4 剪切波速计算结果对比图Fig.4 Comparison of shear wave speed calculation results
2 粗粒土剪切波速试验
2.1 试验材料
为了与实际工程接近,本次测试剪切波速所用的粗粒土取自京雄高铁霸州某标段。根据GB/T50123—2019《土工试验方法标准》,开展了筛分试验,得到了试验粗粒土填料的级配曲线如图5所示。通过击实试验确定了试验粗粒土填料的最优含水率为5.5%,最大干密度为2.24 g/cm3。
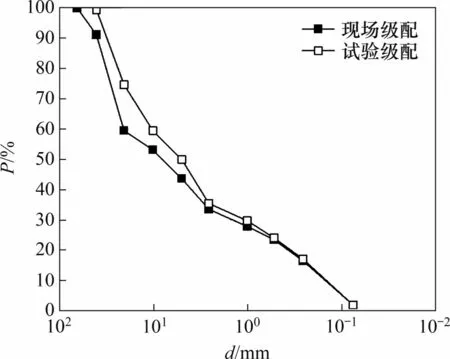
图5 填料级配Fig.5 Filler gradation
2.2 试验设备
室内振动压实试验设备采用课题组自主研发的大型智能振动压实仪,该新型智能振动压实仪主要由机架、振动系统与控制系统组成,其构造如图6所示。振动系统主要包括配重块、偏心块、激振头与激振电机。控制系统由位移计和数据采集软件组成,其中数据采集软件可通过控制变频器对电机转速进行调节,实现对变频器启停控制、工作状态的实时监控,可控制振动频率为0~80 Hz。通过位移计,采用表面沉降法,实现压实密度的自动监测,形成压密曲线。压实仪的质量为200 kg,配重块的质量调节范围为0~400 kg,偏心距的调节范围为0~8 cm,偏心块质量为2.4 kg。

图6 试验设备Fig.6 Test equipment
目前,学者们采用下式直接测试剪切波速vs:
式中:l0为激发剪切波装置与接收装置间的距离;ts为激发剪切波装置与接收装置间传播时间。
然而,针对粗粒土剪切波测试方法鲜有相关研究,需要提出合理的剪切波速测试方法。影响剪切波速的试验因素主要包括激发波形和激发频率2 个因素[25]。本文剪切波速试验采用英国GDS弯曲元系统,该设备不但可以实现正弦波、方波等激发波形的调节,而且可以激发不同频率的剪切波。
2.3 试验方案
首先,研究了激发波波形和激发波频率对于剪切波速测试结果的影响,获得准确的剪切波速测试值。
然后,提出合理的粗粒土填料剪切波速测试方法。
最后,根据此方法测试不同压实密度下粗粒土的剪切波速,并与理论计算对比,验证剪切波速-压实密度理论公式适用性。试验工况如表2所示。
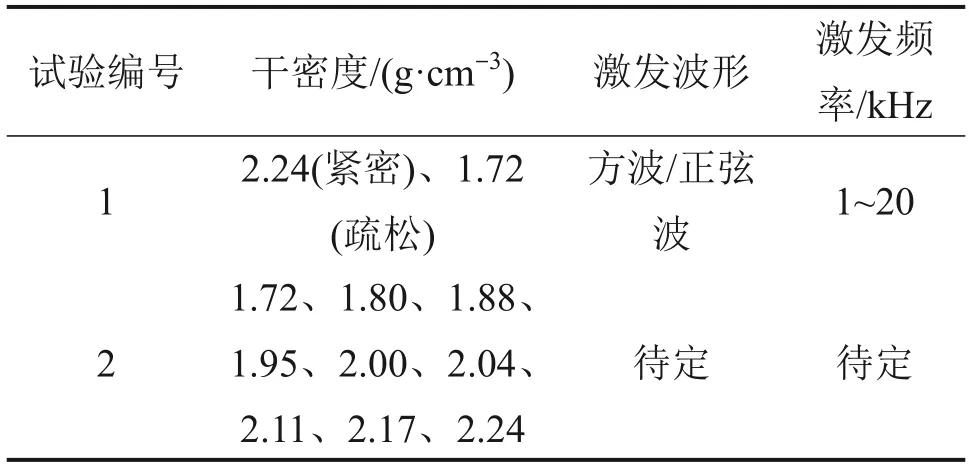
表2 试验工况Table 2 Test conditions
3 试验结果
3.1 激发信号波形的影响
粗粒土处于疏松状态和紧密状态下,分别采用方波和正弦以10 Hz 频率激发,结果如图7所示。

图7 不同激发波形测试结果Fig.7 Test results of different excitation waveforms
由图7 可知:不论激发波形如何,接收波形均为正弦波。以图7(a)为例,当填料干密度为2.17 g/cm3时,根据接收波波形图,以剪切波初至时间点计算得到剪切波速,对于正弦波激发的情况,激发波在0 ms 初激发,而接收波的初至点出现在0.474 ms,时间差为0.474 ms,减去弯曲元系统传播时间0.035 ms,实际传播时间为0.439 ms,粗粒土填料高度为118.7 mm,根据式(22)计算出剪切波速为270.4 m/s。而对于方波激发的情况,计算出剪切波速为266.1 m/s。当粗粒土填料干密度较小时,正弦波激发无法得到可辨认的接收波形图,而采用方波激发却可以得到有效的接收波波形图。而当粗粒土填料干密度较大时,正弦波、方波激发均可得到有效的接收波形。可见,方波激发具有更广泛的适用性。
3.2 激发频率的影响
粗粒土处于疏松状态和紧密状态下,采用方波激发,激发频率分别为1、2、5、10 和20 Hz,测试结果如图8所示。由图8可知:不同频率的激发波对于剪切波速测试的效果有非常明显的影响;当所用激发频率较低时,激发波波长小于剪切波传播距离,接收波形难以发生明显变化,几乎无法获取任何有效的信息;当激发频率增大、激发波波长大于剪切波传播距离时,可从接收波形图中获得有效的信息。当激发频率为5~10 kHz 时,可以得到清晰有效的接收波形图,据此可对剪切波速进行计算。接收波频率并不随激发波频率变化而成倍变化。
干密度较大的粗粒土填料接收波形图清晰度更高,而干密度较小的试样接收波形噪声较多,这主要是由于压实系数较高的试样密实性更好,剪切波更接近于在均匀连续各向同性的理想介质中传播,减少了杂波的干扰及能量的损耗。
3.3 粗粒土干密度预测模型
为验证所提出的粗粒土剪切波速-干密度理论方程适用性,通过文献调研[26-33],列出常规粗粒土的宏细观物理力学参数,并以此对理论公式中参数赋值。表3所示为文献[26-33]中粗粒土参数取值统计。参考文献[26-33],并结合本文材料的相关性质,理论方程中的计算参数如表4所示。

表3 文献[26-33]中粗粒土参数取值统计Table 3 Parameter value statistics of coarse-grained soil in Refs.[26-33]
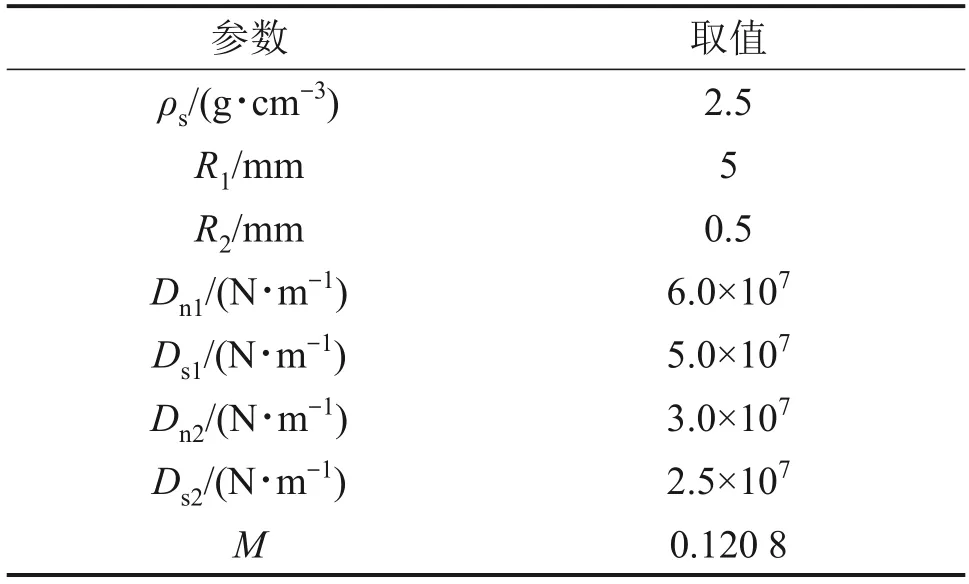
表4 理论公式参数取值Table 4 Theoretical formula parameter value
将选取的材料参数代入式(20),可得如下剪切波速-密度方程:
将所得粗粒土剪切波速与密度关系式绘制曲线,结果如图9所示,并与相应工况试验测试结果对比。从图9可见:理论公式可以较好地预测测试结果。在实际工程中,求出所用材料的M,其后在工程现场可通过测量压实填料的剪切波速来计算土体密度。
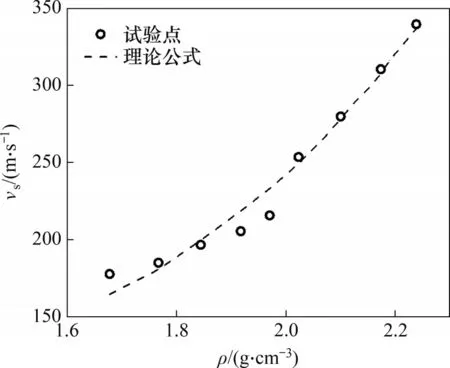
图9 理论与实测剪切波速对比图Fig.9 Comparison of theoretical and measured shear wave velocities
4 结论
1)通过弹性动力学与颗粒细观接触理论,基于粗粒土细观特性(包括颗粒的刚度、配位数、孔隙率、密度),推导粗粒土剪切波速-压实密度的理论计算方程。在计算方程中,颗粒的泊松比对剪切波速的影响不大,而颗粒弹性模量对剪切波速的影响较大。
2)通过周期边界理论,采用Comsol 数值软件来模拟无限空间土体中传播的剪切波,根据数值模型中频率与波矢之间的频散关系得到波速,数值结果与理论计算结果变化趋势相同,且相对误差均在8%以内。
3)剪切波速随压实密度增加而增加。5~10 kHz是合适的激发频率范围,在此频率范围内,不论何种激发波,接收波形均为正弦波,但方波激发具有更广泛的适用性。
4)试验结果验证了剪切波速-压实密度方程的适用性。在实际工程应用中,求出所用粗粒土填料的M,可通过粗粒土填料的剪切波速来快速计算其压实密度。
