基于改进BP算法的模具零件表面抛光质量预测研究

2023-10-29刘守河易建业

模具工业 2023年10期

刘守河，易建业，谢晖，2

（1.季华实验室，广东佛山 528200；2.大捷智能科技（广东）有限公司，广东佛山 528225）

0 引言

随着工业机器人智能自动化技术的迅速发展，工业机器人自动研磨抛光技术因具有作业强度低、环境好、打磨质量一致性好等优势，广泛应用于航空航天、车辆、家电、船舶等领域[1]。模具作为制造业中工艺装备和现代工业制造的基础，是衡量制造业水平的重要标准之一，在汽车、电子、机械制造及航空航天等领域中承担着重要的作用[2]。模具零件表面处理尤其是汽车冲模零件表面的精加工是保证工件表面质量的关键[3]，但因其型面复杂，表面质量要求也较高，所以较多汽车冲模零件表面复杂曲面的研磨、抛光等工序仍依靠熟练工人的手工操作，不但生产效率低，而且对人工技能要求较高。在模具制造过程中，实现机器人全自动化、智能化研合、抛光[4-6]，对提升模具零件表面研磨、抛光品质，减轻模具制造人员劳动强度，缩短模具制造周期具有重要意义[7]。

在模具零件表面自动化抛光过程中，为保证研磨抛光后的表面质量满足需求，需要不断调试、优化抛光工艺参数，导致打磨、抛光工艺参数的调试周期长，效率低，且针对不同的产品需求，抛光工艺参数的适应性较低，因此对模具零件表面抛光质量预测以及抛光工艺参数优化的研究尤为重要。

目前，针对模具零件表面抛光主要集中于模具自动化抛光轨迹、表面质量、磨具材质、基于材料去除理论的抛光工艺参数等的研究。其中，马长捷[8]基于Preston 理论建立材料去除函数的理论模型，并进行仿真分析，总结了打磨工艺参数对于抛光表面质量的影响规律；张雷等[9]利用多元线性回归正交试验建立了模具零件曲面抛光工艺过程模型，通过仿真和试验结果表明该模型综合反映了抛光工艺参数对抛光效果的影响规律；陈满意等[10]提出了一种能够适应系统刚度变化的模糊自适应阻抗控制模型，该模型通过提供稳定的法向力控制和位置控制，提高了模具零件表面抛光质量；ZHAO T 等[11]为提高表面抛光质量，通过单因素试验获取了抛光工艺参数的优化范围，并利用二次非线性回归方法建立了表面粗糙度预测模型。针对工艺参数优化、表面质量预测问题，目前已有学者基于不同模型进行了大量研究。韩天勇等[12]研究了刀具转速、抛光力、行间距、机器人进给速度对零件表面抛光质量的影响，基于PSO-SVM 方法建立了曲面零件抛光粗糙度预测模型；李健等[13]提出一种改进后的粒子群神经网络模型，用于识别刀具的磨损状态；潘杰等[14]基于工件表面材料去除原理，建立了抛光工艺参数与材料去除率和表面粗糙度的数学模型，得出影响抛光质量的工艺参数，并基于SPSO-BP 方法建立了抛光后工件表面质量的预测模型。

目前，机器算法被广泛应用于工艺参数优化领域。模具自由曲面抛光是多工艺参数耦合相互作用的过程，抛光后的表面质量取决于多项评价指标，为了研究模具零件抛光后表面质量预测及工艺参数优化问题，现通过采集模具抛光后的表面质量参数，作为测试样本集，将混沌理论、动态权重、动态学习因子和高斯变异方法引入粒子群寻优算法（particle swarm optimization，PSO），利用改进后的粒子群寻优算法（improved particle swarm optimization，IPSO）对神经网络（back propagation，BP）模型中的权重和阈值更新策略进行优化，实现了对模具零件抛光后的表面粗糙度和去除量的预测，并结合快速非支配排序遗传算法（NSGA-II）建立多目标优化模型，实现对模具零件抛光工艺参数的优化。

1 模具零件表面抛光分析

模具零件自由曲面抛光后的表面质量一方面与机器人抛光系统有关；另一方面与主轴转速、抛光压力、步距、机器人进给速度、磨头目数等工艺参数有关。现主要对模具零件表面抛光过程进行受力分析，并建立模具零件表面抛光去除模型。

1.1 弹性磨头与模具零件表面接触分析

图1所示为弹性芝麻粒磨头与待加工工件曲面的接触简图，其中磨头半径为R，抛光力为F，磨头转速为ω，弹性磨头主轴方向与模具零件接触面法线方向夹角为α，接触压力为Fn，满足Fn=Fcosα。

图1 弹性磨头与模具零件自由曲面接触简图

将模具零件抛光过程简化为弹性体与刚性曲面接触，接触区域如图2所示，弹性磨头与模具零件自由面的接触区域近似为椭圆，依据Hertz 理论，接触区域内任意一点(x,y)的接触压力[15]可以表示为：

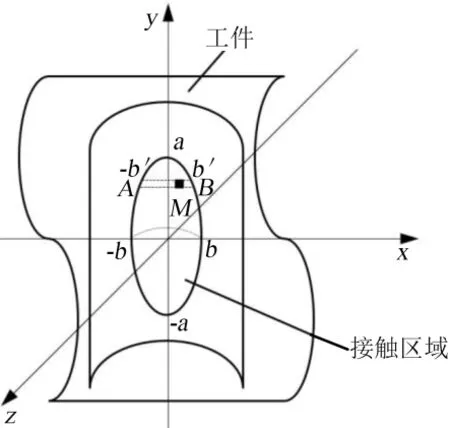
图2 抛光接触区域

其中，a，b分别为椭圆接触区域的长、短半轴。弹性磨头与模具零件表面的相对运动速度也会影响模具零件表面的抛光去除量，对于接触区域内任意一点A(x,y)，建立接触区域速度矢量模型，如图3所示。

图3 接触区域速度矢量模型

接触区域内任意一点(x,y)的速度为：

其中，δ表示弹性磨头变形量。

1.2 模具零件表面抛光去除模型

在抛光加工领域，研究人员通常采用Preston 方程建立材料去除模型，其描述了在抛光加工过程中的材料去除量与抛光工艺参数之间的关系，具体表达式为：

其中，Kp为Preston 常数，一般由试验确定，与磨头材质与工件硬度有关；v为弹性磨头与工件之间的相对速度；p表示接触区域内弹性磨头与工件之间的接触压力。

材料去除量可以表示为：

其中，vs表示磨头某点的切向线速度；vf表示磨头沿工件的进给速度。

图2所示的微元M的材料去除量可以表示为：

2 试验设备和方案

2.1 机器人自动化抛光平台和抛光质量检测系统

模具零件自动化抛光试验平台主要由机器人、主轴电机、恒力浮动装置、七轴移动平台等组成，如图4所示。模具零件表面抛光质量检测主要包括粗糙度检测和表面去除量检测，其中抛光后工件表面粗糙度由手持便携式粗糙度测量仪测量，工件表面去除量由三坐标测量仪测量，如图5所示。

图4 机器人自动抛光设备

图5 表面质量检测

2.2 试验步骤及方案

在建立模具零件表面抛光质量预测模型之前需要获取一定数量的工艺试验数据，通过前期的试验总结，分析了影响抛光后模具零件表面粗糙度和模具零件表面去除量的工艺参数，其中主要包括抛光工艺参数和弹性磨头参数，选取主轴电机转速N、打磨压力F、进给速度V、磨头目数K、磨头直径D作为设计变量，模具零件表面粗糙度Ra和模具零件表面去除量S作为目标变量。根据抛光工艺参数调试经验和弹性磨头参数型号确定各设计变量取值范围，如表1所示。

表1 设计变量取值范围

采集96组试验样本数据，部分样本数据组合如表2所示。

表2 试验样本数据

抛光试验材料为120 mm×220 mm×30 mm 的SKD11 模具钢，抛光工具为弹性芝麻粒磨头，部分芝麻粒磨头参数如图6 所示，打磨轨迹均为往复路径，如图7所示。

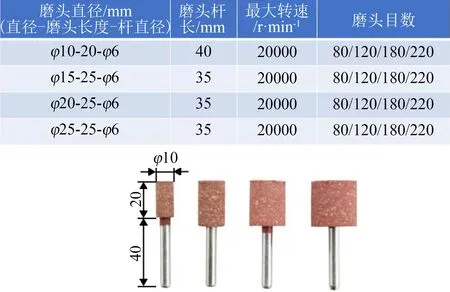
图6 芝麻粒磨头参数

图7 磨头打磨路径

完成试验方案中所有试验组合后，对抛光后的试验样件的表面粗糙度和去除量进行测量，利用手持粗糙度仪测量样件表面粗糙度（见图5），测量时选取抛光区域均匀分布的4 个测点，每点的取样长度为0.8 mm，每个点测量5 次。完成表面粗糙度测量后对样件表面去除量进行测量，采用龙门式三坐标测量仪，对样件抛光前的表面进行基准测量，采集样件表面均匀分布的9 组点位进行测量，获取样件抛光前的基准值。样件抛光后，对相同点位进行测量，将抛光区域内的点位测量值与基准值进行对比，取区域内所有测点差值的平均值作为最终表面去除量。表3 所示为测量得到的部分试验数据结果。

3 模具零件表面抛光质量预测模型与方法

3.1 BP神经网络

人工神经网络利用训练样本，通过自身不断地训练进而学习模型输入量和输出量之间的非线性映射规则，实现对输出量预测的数据信息处理系统。在众多神经网络模型中，BP神经网络是一种应用较广泛的多层前馈神经网络模型[16]，主要包括输入层、隐含层、输出层以及层与层之间的权值和阈值。

现引入BP 神经网络构建模具零件表面抛光质量的预测模型，预测模型包含输入层、隐含层和输出层，图8所示为神经网络训练模型结构，其中模型的相应参数如下。

图8 神经网络训练模型结构

（1）输入层节点。将影响抛光后模具零件表面粗糙度Ra和表面去除量S的工艺参数作为输入层节点，即选取主轴电机转速N、打磨压力F、进给速度V、磨头目数K、磨头直径D作为模型的输入节点。

（2）输出层节点。将模具零件抛光质量评价指标表面粗糙度Ra和表面去除量S作为神经网络模型的目标预测量，即选取粗糙度Ra和去除量S作为模型的输出节点。

（3）隐含层神经元数。隐含层神经元数确定通常参考Kolmogorov 定理并采用试凑法[17]，隐含层神经元的个数通过经验公式确定，选取隐含层神经元节点为6。

（4）激活函数。隐含层和输入、输出层每个神经元节点之间的关系可以表示为：

其中，xi为神经元输入量；ξi为输入量权值；φ为神经元阈值。

选用Sigmoid函数作为激活函数，其表达式为：

3.2 IPSO-BP算法

在BP神经网络预测模型中，采用梯度下降的更新策略对预测模型的权值和阈值进行更新，容易获取局部最优解。采用IPSO 算法改进预测模型中权值和阈值的更新策略，以获取全局最优解。

PSO 算法由于具有较强的全局和局部搜索能力，常用于解决优化配置、参数优化等问题。PSO算法在可行解空间内随机生成粒子初始种群，各粒子的位置都对应寻优问题的解值，通过不断更新粒子的位置和速度寻求在可行解空间的最优值。

在迭代寻优过程中，粒子的速度和位置可以表示为：

其中，xi、vi分别表示第i个粒子的位置和速度；qi表示粒子个体极值；pi表示粒子种群极值；ω∧为惯性权重；j为寻优空间维数；t为迭代次数；c1、c2为学习因子；r1、r2为[0,1]内的随机数。

在搜寻过程中，PSO 算法可能会由于种群多样性降低以及种群分布不均匀，陷入局部最优搜寻，影响算法优化性能。现通过耦合混沌理论、动态权重、动态学习因子和高斯变异方法，改进了粒子群优化算法，其具体流程如下。

（1）利用混沌映射的随机性、遍历性及初值敏感性的特点，将其用于初始化PSO 粒子种群，提高种群的多样性和均匀性，现采用Tent 映射方法初始化PSO种群。

（2）Tent混沌映射序列：

（3）将Tent混沌映射序列映射到搜索空间：

利用Tent 映射方法初始化PSO 种群，使其遍历搜索空间，提高算法的最优搜寻概率。

（4）为了保证PSO 算法全局寻优以及局部寻优能力，引入动态权重方法，提高算法稳定性以及收敛速度，其可以表示为：

（5）构造动态学习因子，为了平衡算法的全局寻优能力和局部寻优能力，满足在算法初期注重粒子个体寻优解，后期注重粒子群体寻优解，在粒子速度更新公式中引入动态学习因子，其表达式为：

其中，c1_max、c1_min、c2_max、c2_min分别表示学习因子c1、c2的最大、最小值，具体值为2.1、0.8、2.1、0.8。

（6）为了避免PSO 算法在后期陷入局部最优解，在粒子速度更新公式中粒子个体项引入高斯变异项，提高算法跳出局部最优解的能力，引入高斯变异项后的粒子速度可以表示为：

其中，k1、k2为[0,1]的随机数表示高斯变异值；ε为均值；σ2为方差。

为了验证IPSO 相比于PSO 算法的收敛精度高，分别利用单峰测试函数（F1,F2）和多峰测试函数（F3,F4）对IPSO 进行测试，测试函数表达式如表4 所示。独立运行20 次后，测试结果如表5 所示，收敛曲线如图9所示。

表4 测试函数表达式

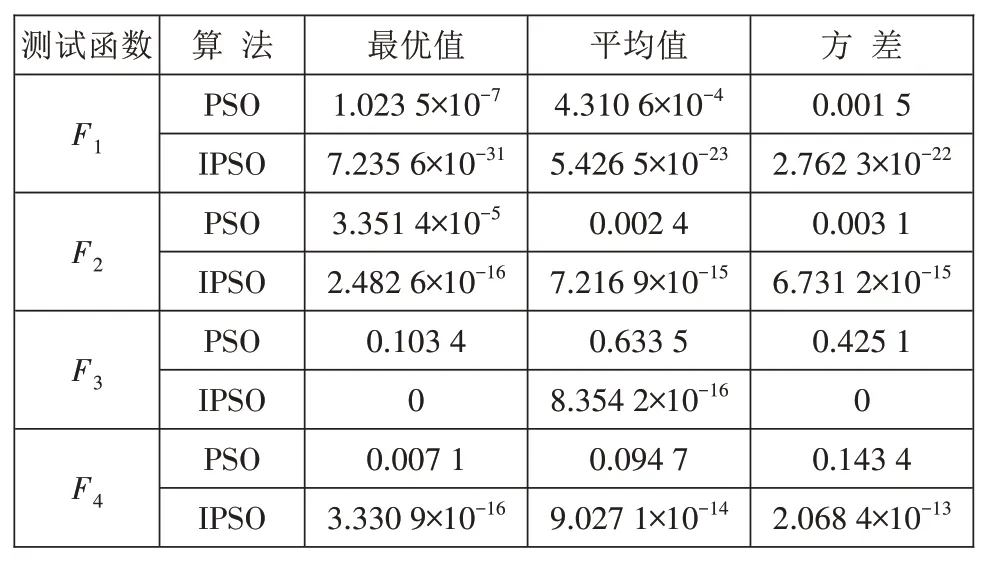
表5 测试结果

图9 IPSO和PSO算法对测试函数的收敛曲线

由表5 可知，从最优值、均值和方差3 个维度分析，IPSO 在有限迭代次数下其收敛精度均高于PSO，故耦合混沌理论、动态权重、动态学习因子和高斯变异方法的IPSO 具有更强的参数寻优能力；从图9可以看出，IPSO算法的寻优速度更快，可以用于对BP 预测模型的优化。IPSO-BP 预测模型流程如图10所示。

图10 IPSO-BP预测模型流程

3.3 模具零件表面抛光质量预测模型

模具零件表面抛光质量预测模型如图11所示，预测模型主要包括预测目标函数、预测模型输入参数和预测模型算法。在预测目标函数中，g(U)表示模具零件表面质量参数（粗糙度Ra和表面去除量S）与预测模型输入参数集U之间的非线性关系。在预测模型输入参数集U中，主要包括抛光工艺参数和弹性磨头参数，即主轴电机转速N、打磨压力F、进给速度V、磨头目数K、磨头直径D。在预测模型算法中，定义了求解预测目标函数的方法集IPSOBP，其中包括混沌理论、动态权重、动态学习因子和高斯变异方法和PSO 的IPSO 算法以及BP 预测模型。

图11 模具零件表面抛光质量预测模型

4 模具零件表面抛光质量预测结果分析

以不同误差评价指标为依据，对比不同预测模型的预测结果阐述基于IPSO-BP算法的模具零件表面抛光质量预测模型的实际效果。采用以下误差指标对预测模型的预测精度进行评价，如表6所示。

表6 预测模型误差指标

4.1 预测结果

利用获取的采样样本作为输入参数集，以抛光工艺试验测量获取的模具零件表面抛光质量结果作为训练样本集，其中有效样本集为96 组，将其划分为训练集（80组数据）和测试集（16组数据）。

预测模型训练步骤如下：①确定预测模型输入神经元与输出神经元个数；②初始化粒子种群数量初步设定为30，tmax初步设定为300；③完成对训练样本集的归一化处理；④利用改进后的粒子群寻优算法对BP 模型权值和阈值进行更新；⑤基于IPSOBP 预测模型对试验样件抛光后的表面粗糙度和表面去除量进行预测，预测结果如图12所示。

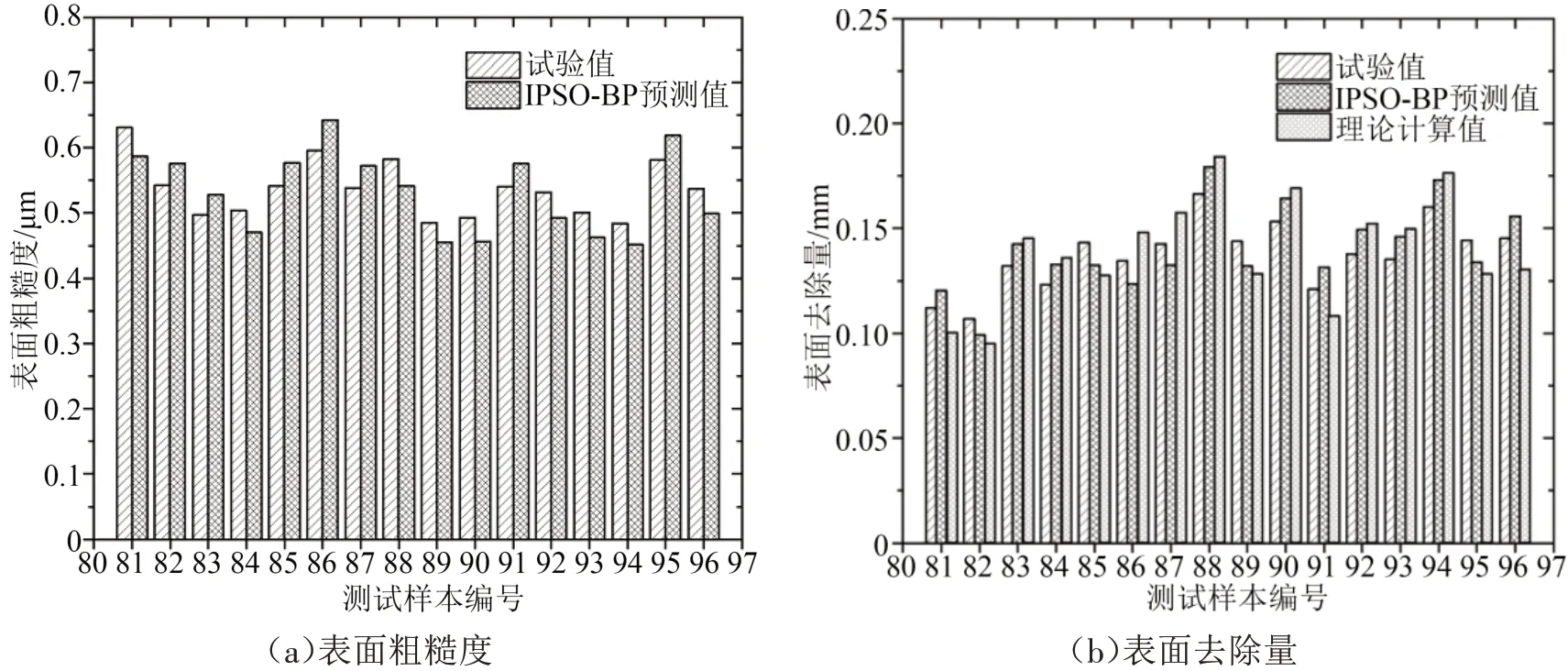
图12 基于IPSO-BP算法的模具零件表面抛光质量预测结果

从图12可以看出，通过抛光工艺试验测量的表面粗糙度和表面去除量与其预测值误差较小，说明建立的基于IPSO-BP方法的预测模型可以较好地预测表面粗糙度和表面去除量。计算预测模型精度评价指标值，包括MAE、MAPE、MSE、RMSE、SMAPE，计算结果如表7所示，预测模型的各项误差指标均处于较低水平，表明预测模型具有一定的稳定性，可以用于对模具零件表面抛光质量的预测。

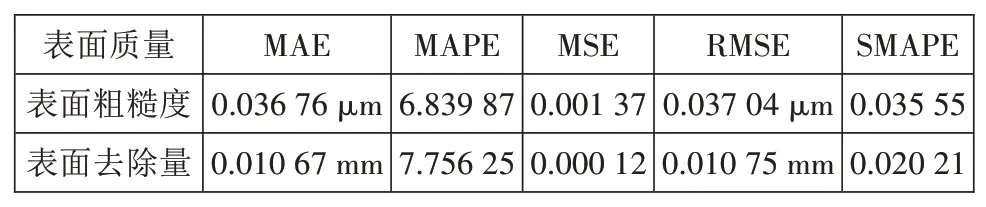
表7 预测模型各项误差评价指标值

4.2 常用预测模型对比分析

为了验证提出的基于IPSO-BP 方法的模具零件表面抛光质量预测模型的优越性，将IPSO-BP 预测模型与基于PSO-BP、BP、支持向量回归（support vector regression，SVR）、多元线性回归（multiple linear regression，MLR）方法搭建的常规预测模型以及理论计算值进行对比。常规预测模型和理论计算值的结果如图13 所示，常规预测模型和基于IPSO-BP方法的预测模型都可以用于预测粗糙度和表面去除量，但相比于常规预测模型，改进后的IPSO-BP预测模型具有更高的预测精度。

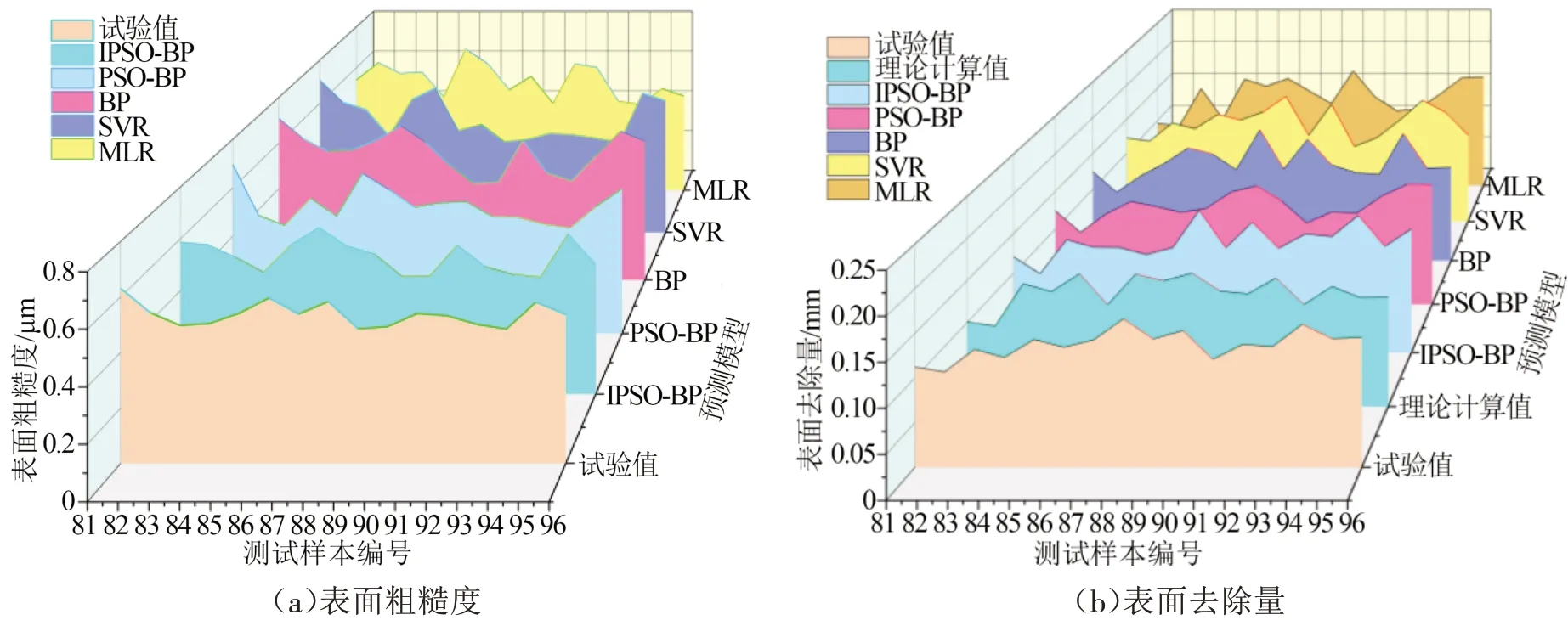
图13 常规预测模型预测结果对比

利用MAE、MAPE、MSE、RMSE、SMAPE 等误差指标对预测模型进行对比分析，对比结果如图14以及表8、表9 所示，相比于常规预测模型，基于IPSOBP 方法的预测模型误差评价指标更小，对比IPSOBP 和BP 两种方法可以得出结合IPSO 算法与BP 模型的表面抛光质量预测模型具有更高的预测精度；对比IPSO-BP 和PSO-BP 两种预测方法可以得出通过对PSO 算法耦合混沌理论、动态权重、动态学习因子和高斯变异方法可以进一步提高算法的全局寻优能力，保证了预测模型的精度。与SVR、MLR方法相比，IPSO-BP 方法的误差指标同样最小，进一步表明基于IPSO-BP方法搭建的预测模型在预测抛光表面粗糙度和表面去除量问题上优于常规预测算法。

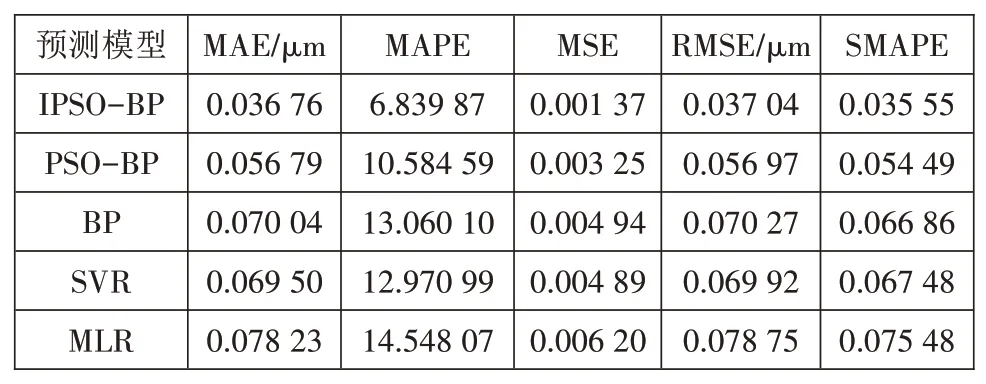
表8 表面粗糙度预测结果分析

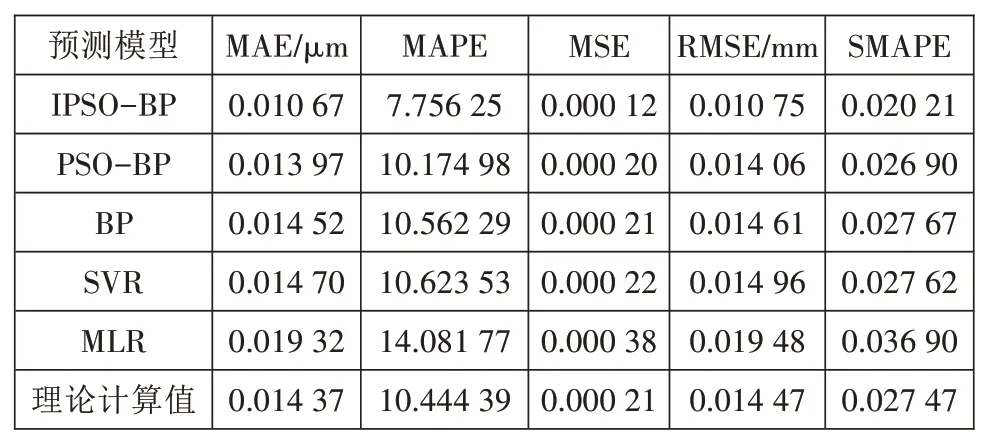
表9 表面去除量预测结果分析

图14 预测模型评价指标对比分析

综上所述，构建的基于IPSO-BP 模具零件表面抛光质量预测模型具有预测精度高、寻优速度快等特点，可以用于模具自动化抛光工艺调试阶段，实现对模具零件表面抛光质量的快速预测，缩短模具自动化抛光工艺调试周期，降低抛光工艺调试成本。

4.3 基于NSGA-II算法多目标优化

NSGA-II 是在遗传算法的基础上引入了快速非支配排序、聚集距离排序和精英策略理念[18]，其根据个体水平分层，利用非支配解集中解的秩升序排序，具有算法复杂程度低、全局寻优能力强、收敛性好等特点。采用IPSO-BP-NSGA-II 方法实现对模具零件表面抛光预测模型中抛光工艺参数的优化求解，主要流程如下。

（1）建立多目标优化模型。根据模具零件表面抛光质量预测模型的数学模型，将抛光后表面粗糙度Ra和表面去除量S作为优化目标，多目标优化模型可以表示为：

（2）建立约束条件。约束条件是模具抛光过程中各工艺参数水平的取值范围，由抛光工艺参数调试经验和弹性磨头参数型号决定，各工艺参数的约束条件为：

（3）最小值目标优化。采用最小值求解法优化各工艺参数，对表面去除量目标函数取反，最终多目标优化模型可以表示为：

其中，φ、η表示权重因子。

基于NSGA-II算法对模具零件表面抛光工艺参数进行优化，种群大小为200，迭代次数为300，适应度函数偏差为0.001，优化后的工艺参数如表10所示。