一道与旋转有关的动点最值问题的探究

李幽兰

⦿ 湖北省武汉市吴家山第二中学

初中平面几何中,由图形运动而产生的最值问题历来是学生解题的难点,究其原因是图形一直在变化,学生无法捕捉到运动变化背后“不变”的元素,难以分析出取最值时变化元素的位置,也就无法根据具体图形分析求解[1]．其中,与旋转有关的动点求最值问题,热度一直高居不下,近几年常“驻”各地中考选填题和几何综合题的压轴位置,令莘莘学子头疼畏惧.下面笔者分享一道题目的解法和变式的深入探究,希望给读者一点启发.

图1

解法1：(坐标法)分别过点Q和Q′作x轴的垂线,垂足分别为点M和N,如图2.

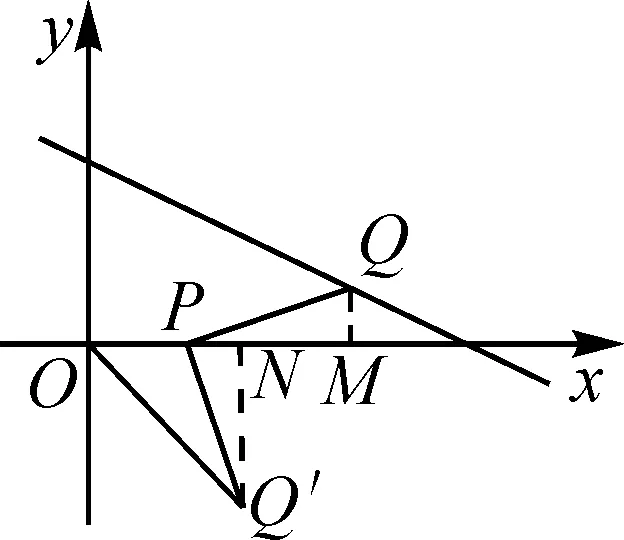
图2

于是∠QMP=∠PNQ′=90°,则∠PQ′N+∠NPQ′=90°.

因为∠QPQ′=∠QPM+∠NPQ′=90°,则∠PQ′N=∠QPM.

又PQ=Q′P,所以△PMQ≌△Q′NP(AAS).

故PM=Q′N,QM=PN.

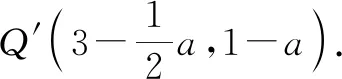
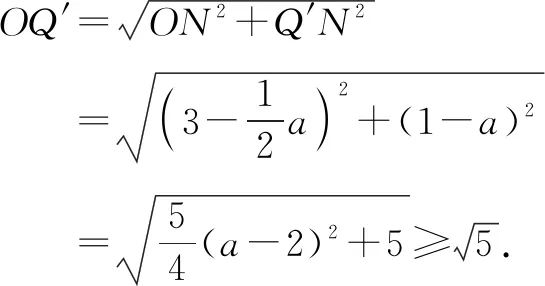
故选答案:B.

点评：解法1抓住平面直角坐标系中的有利条件,构造了 “一线三垂直”模型证三角形全等.首先设未知数表示出动点Q的坐标,用坐标来表示线段长度进行转化,然后由勾股定理表示两点之间的距离,用含x的式子将OQ′表示出来,最后运用二次函数的知识求出最值.这种方法虽然很巧妙、简便,但是有一定的局限性,只能用于有坐标系且旋转角度特殊的题目.

解法2：(轨迹法)如图3,将△AOB绕点P顺时针旋转90°得到△A′O′B′,则Q′为直线A′B′上一动点,根据垂线段最短,OQ′的最小值为点O到直线A′B′的垂线段的长度d.

图3

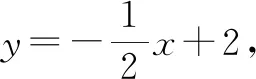
由题意,得O′(1,1),A′(3,1),B′(1,-3).

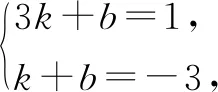
点评：解法2由旋转的本质出发,直线AB绕点P顺时针旋转90°所得直线A′B′即为动点Q′的轨迹,但直接求直线A′B′的解析式不方便,因此旋转整个△AOB,先求出点A′和B′的坐标,再求直线A′B′的解析式,最后用面积法求出点O到直线A′B′的距离.当然,在求出了直线A′B′的解析式后,也可以由此设Q′的坐标,用解法1中的坐标法,运用勾股定理和二次函数来求最值.解法2适用于大部分的动点旋转求最值问题,即先确定动点轨迹.

图4

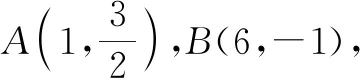
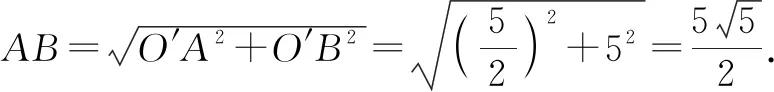
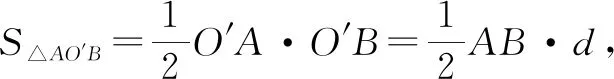
变式1在Rt△AOB中,OA=2,AB=4,P是OB上一点,OP=1,Q是边AB上的一个动点,将Q绕点P逆时针旋转30°得到点Q′,连接OQ′,则OQ′的最小值为______.

解析：点Q在AB上运动,即点Q的轨迹为AB,那么将AB绕点P旋转就能得到点Q′的轨迹.于是,将△AOB绕点P逆时针旋转30°得到△A′O′B′,如图5,则点O到A′B′的距离即为OQ′的最小值.

图5

由旋转,得∠BPB′=30°.

在Rt△AOB中,OA=2,AB=4,所以∠B=∠B′=∠BPB′=30°,于是A′B′∥OB,则∠AEB′=∠AOB=90°.

所以点O到A′B′的距离为OE的长度.

如图5,过点B′作B′F⊥OB于点F,则∠B′FP=90°,于是四边形OEB′F是矩形.

变式1没有坐标系背景,显然解法1不适用,而运用解法3,将点O绕点P顺时针旋转30°以后再求O′到AB的距离较为麻烦,经对比发现,此题解法2是最简便的.

类似地,还可以变化图形形状和旋转角度,解法一样.

变式2如图6,在等腰三角形ABC中,∠BAC=120°,AB=AC,D是AB上一点,AD=2,BD=4,E是边BC上的动点,若点E绕点D逆时针旋转30°的对应点是F,连CF,则CF的最小值是______.

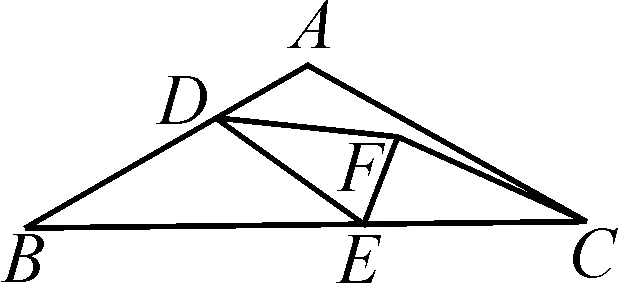
图6

基于以上分析,我们可以总结:解决这类绕定点旋转的最值问题有三种方法,分别为坐标法、轨迹法、逆向轨迹法,根据不同的题目来选择合适的方法,最常用的是轨迹法.若是动点所在的直线绕定点旋转,则先确定动点旋转后的轨迹,再根据垂线段最短求点到直线的距离,最后解直角三角形得到所求最值.

动态问题解题的关键是在“动”中寻找“定”的量,再由这些定量探寻出动点形成的轨迹,从而根据轨迹分析出最值位置,即“由动寻定,由定定轨,由轨求最”[2]．题目只是知识方法的一个素材,解题的过程能让学生理解知识的原理,提炼方法的本质,注重解法的策略,总结问题的归类,从而达到利用有限的题目实现无限的再创造．由解一道题变成会解一类题,乃至通解一种体系的题,这也是解题教学的方向[1].