采用知识迁移加速的智能气动设计优化方法

郭振东,李存晰,宋立明,李军,丰镇平

(西安交通大学能源与动力工程学院,710049,西安)

气动形状优化作为飞机翼型和航空发动机叶片设计的重要环节,一直是国内外学者研究和关注的重点[1-4]。飞机翼型和航空发动机叶片的形状多采用自由曲线/曲面设计,由于设计时输入设计参数与输出目标性能之间的函数关系无法用显式表达[5],且气动性能评估通常非常耗时,所以是典型的昂贵黑盒子问题[6]。通常,气动形状优化包括3个关键环节,即气动形状设计空间参数化、优化算法和性能评估。常用的参数化方法包括非均匀有理B样条(non-uniformed rational B-spline,NURBS)法、自由网格形变 (free-form deformation,FFD)法等[7]。近年来,基于深度学习的智能参数化方法如 Bezier-GAN法[8]、AirfoilGAN法[9]等亦被提出用于翼型参数化建模。在确定气动形状设计空间后,代理模型优化算法等全局类优化算法被广泛用于气动设计空间寻优[10-11],而计算流体动力学 (computational fluid dynamics,CFD)方法则被用于对优化个体进行性能评估。

随着气动形状设计要求的不断提高,精细气动形状设计优化面临如下困境:一方面,为满足日益苛刻的性能指标要求,设计人员往往会增加参数化设计空间的维度,以期实现更精细的气动型线调整,囊括性能更优的设计样本[12],但随着设计空间变量维度的增加,采用全局类优化算法探寻设计空间最优解所需样本的评估次数将以指数形式急剧增加[10-13];另一方面,日益精细的气动形状设计通常采用非定常计算等更高精度的CFD评估手段对飞机翼型、航空发动机叶片进行性能评估[14-15],而非定常计算等高精度评估方法相对于传统常用的定常计算,所需的计算资源急剧增加,在规定的任务周期内所能容许的高精度性能评估次数非常有限。为此,如何平衡上述两个方面的矛盾,即如何缩短“精细化设计优化所需的最少性能评估次数”与“任务周期内所能容许的最大性能评估次数”之间的差距,是当前气动形状设计优化方法研究无法回避的难题。

另外需要特别指出的是,在当前绝大多数气动形状设计优化过程中,当优化目标和参数化设计空间确定后,优化算法往往“从零开始”对设计空间寻优。与此类传统优化方法不同的是,设计人员通常能不断地从已完成的任务中提取经验,用于指导新任务的求解[16-17]。受到上述启发,“知识迁移”理念在机器学习及计算智能领域得到了广泛关注,相关研究又被称为“迁移学习 (transfer learning)”[17]和“迁移优化 (transfer optimization) ”[18-19],其核心思路是让机器学会像人一样累积经验,从已完成的类似任务中智能汲取有用信息,用于减少目标任务求解成本,并进一步提升目标任务优化解性能。

近年来,知识迁移理念在航空发动机设计领域亦受到重视[20-21],Rolls-Royce研究团队已着手于将知识迁移理念用于航空发动机总体设计建模,测试结果表明相对于传统方法,采用知识迁移策略可将设计效率提升80%[22]。然而,将知识迁移理念推广到飞机翼型、航空发动机叶片形状的设计优化时,仍需解决如下两个方面的问题:①如何将已完成的类似任务优化解集编码至目标任务参数化设计空间,即如何将已采用NURBS、FFD及Bezier-GAN等不同方法进行参数化建模的已完成任务优化解编码至目标任务参数化设计空间;②如何提取已完成任务样本中所包含的有用设计信息,用于促进目标优化任务的求解。

针对以上两方面问题,本文采用深度学习模型变分自编码器(variational autoencoder,VAE)[23],将已完成的相关任务优化解集编码至目标任务参数化设计空间;接着,采用多保真度高斯过程[24-25]从已完成任务的样本中提取有用信息,促进目标任务的求解;最后基于上述思路,建立了气动形状迁移优化方法,并通过基准数值算例开展测试与翼型气动型线优化分析,验证了知识迁移策略的有效性。

1 迁移优化简介

如图1所示,迁移优化的基本思路即让优化算法像人一样累积经验,从已完成的相关任务S1,…,Sm中汲取有用信息,并形成知识库K(t),用于指导目标任务T的求解[18]。相应的目标优化任务表达式可表示如下

(1)

(2)

除经典的迁移优化方式外,在同一问题的不同形式间相互汲取有用信息的多平台迁移优化亦被提出,其原理如图2所示。多平台迁移优化原理的基本思路为寻找可对目标任务T进行简化的问题T1,…,Tk,和目标任务T一起求解,并在优化过程中不断从T1,…,Tk以及T中提取有用设计信息,形成知识库K(t),以促进各任务的求解,最终实现提高目标任务T的优化效率。其相关表达式如下

(3)

图2 多平台迁移优化原理示意图Fig.2 Schematic of multi-form transfer optimization

2 知识迁移加速的气动设计优化方法

采用知识迁移加速的智能气动设计优化方法包括两个环节:气动形状设计空间参数化和迁移优化算法。下面将在2.1节和2.2节对所提出的采用VAE模型的气动形状参数化方法与贝叶斯迁移优化算法进行介绍,进而在2.3节对所发展的气动型线迁移优化设计框架进行说明。

2.1 采用VAE模型的形状参数化方法

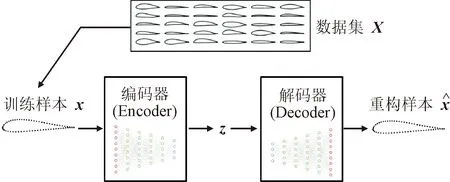
图3 VAE模型气动形状参数化方法原理图Fig.3 Schematic of VAE-based aerodynamic shape parameterization method

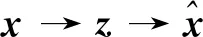
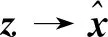
在传统的设计优化过程中,设计人员往往采用NURBS、FFD等方法获得低维参数化设计空间ζ,进而在ζ空间开展型线优化设计。在完成型线优化设计后,设计人员往往会保留以散点坐标表征的真实型线样本x及其性能分析结果文件,却很少保留对应的低维参数化空间样本z。然而,NURBS、FFD等传统参数化方法无法实现从x→z的转换,即很难将已完成任务所获得的优秀型线样本编码至目标任务参数化设计空间。当且仅当已完成任务与目标任务样本可用相同的FFD、NURBS参数化空间表示时,已完成任务样本才能被用于目标任务设计过程,这严重限制了迁移优化策略在气动型线设计优化中的应用。

2.2 贝叶斯迁移优化TGO算法

在建立VAE参数化设计空间实现了将已完成任务样本统一编码至目标任务参数化空间后,仍需解决如何提取已完成任务样本中的有用信息用于加速目标任务的优化进程这一问题。为此,在贝叶斯优化框架下,将基于多保真度高斯过程的序列迁移优化策略与多平台迁移优化策略相结合,研发了贝叶斯迁移优化算法 (transfer learning accelerated efficient global optimization,TGO)。以下将对TGO算法所采用的迁移优化策略及其优化流程进行介绍,并应用算例进行测试。

2.2.1 基于多保真度模型的序列迁移优化

在目标任务参数化设计空间中,假定已完成任务样本集为{zS,yS}m,目标任务样本为{zT,yT}n。基于多保真度模型的序列迁移优化策略的基本思路为,将{zS,yS}m作为目标任务的低保真度样本,利用多保真度高斯过程将{zS,yS}m与{zT,yT}n进行数据融合。上述过程能有效地提高贝叶斯寻优代理模型的预测精度,特别是代理模型在最优值邻域内的预测精度,由此加速目标任务优化进程。

参照原始模型推导过程[26],用于融合{zS,yS}m与{zT,yT}n的多保真度高斯过程预测模型可表示如下

(4)

在构建多保真度代理模型的基础上,通过最大化期望提升(expected improvement,EI)函数对目标函数设计空间进行贝叶斯寻优,其具体表达式如下

(5)

式中:yPBS为当前所获得的最优目标函数值;Φ(·)和φ(·)分别为高斯累积分布函数和密度分布函数;σM(z)为多保真度高斯过程在z处目标函数预测值的标准差。

2.2.2 多平台迁移优化与TGO算法流程

在优化后期,随着目标任务样本增加,直接采用目标任务样本构建的单保真度代理模型精度可能会比融合已完成任务、目标任务样本所构建的多保真度代理模型精度更高[24]。为尽可能提高用于贝叶斯寻优的代理模型精度,进而加速目标任务求解,在图2所示多平台迁移优化思想的启发下,提出同时开展基于单保真度模型和多保真度模型的设计空间寻优。直接采用目标任务样本{zT,yT}n所构建的单保真度预测模型表达式如下[26-27]

(6)

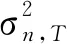
在完成单保真度代理模型构建后,通过最大化EI函数进行设计空间寻优,表达式可写为

(7)

由于同时进行单保真度与多保真度代理模型寻优,在多保真度框架下每次优化迭代将更新2个样本,相关表达式如下

(8)

式中Znew为每步迭代将采样的个体。

图5给出了本文所提出TGO算法的流程图。其中,实线方框对应传统无知识迁移的经典代理模型优化(efficient global optimization,EGO) 算法的执行流程,即仅利用目标任务样本{zT,yT}n构建单保真度代理模型,进而基于式(7)进行设计空间寻优。在EGO算法的基础上,TGO算法融入了基于多保真度代理模型的寻优过程,开展针对同一优化问题的“多任务”寻优过程,并在每次优化结束时,通过交换最优解,用于单、多保真度模型更新,来实现“多任务”信息交换,达到提升优化效率的目的。

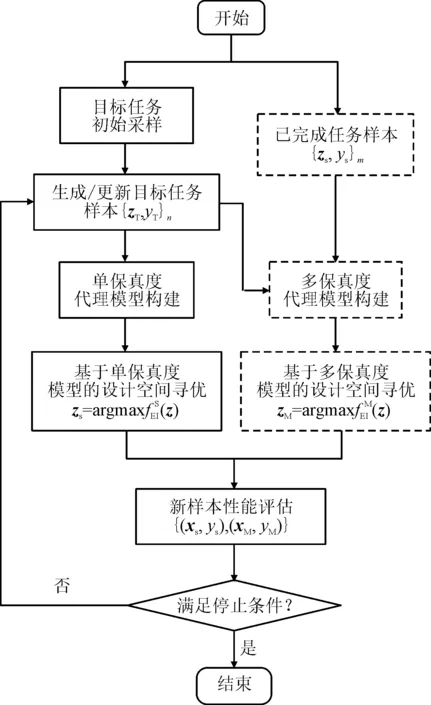
图5 本文所提出TGO算法流程Fig.5 Flowchart of TGO algorithm

2.2.3 数值算例测试

鉴于迁移优化与多保真度优化的相似性,选取经典的多保真度优化基准测试算例,对TGO算法的有效性进行测试,相关函数表达式如表1和表2所示。可以看到,多保真度优化测试中采用的低保真度函数被当作了迁移优化测试的已完成任务函数。

表1 用于TGO算法测试的目标任务与已完成任务表达式

表2 测试函数表达式

由于在实际场景中,已完成任务样本{zS,yS}m的设计空间分布特征无法事先确定,为模拟上述情形,对表1所示已完成任务样本开展贝叶斯优化,将优化完成时所生成的样本集作为{zS,yS}m的候选数据库。此外,注意到用于迁移优化的多保真度建模的核心任务,是利用已完成任务与目标任务的相似性,提高用于贝叶斯寻优的代理模型在设计空间最优值邻域内的预测精度。为此,借鉴Wang等迁移优化研究经验[21],采用最优解准则筛选出已完成任务样本用于TGO优化,即根据目标函数对已完成任务样本进行排序,选取性能最优的数十个样本,用于TGO算法中的多保真度建模过程。

对基准测试函数分别开展10次测试计算,图6分别展示了TGO和EGO算法的均值收敛图,表3展示了10次优化所获得的最优解均值及标准差。易见,相较于传统无知识迁移的EGO算法,TGO算法收敛速度更快,获得的优化解更优,且10次优化的最优解均值和标准差均显著小于EGO算法,由此验证了所提出的采用知识迁移加速的TGO算法的有效性。

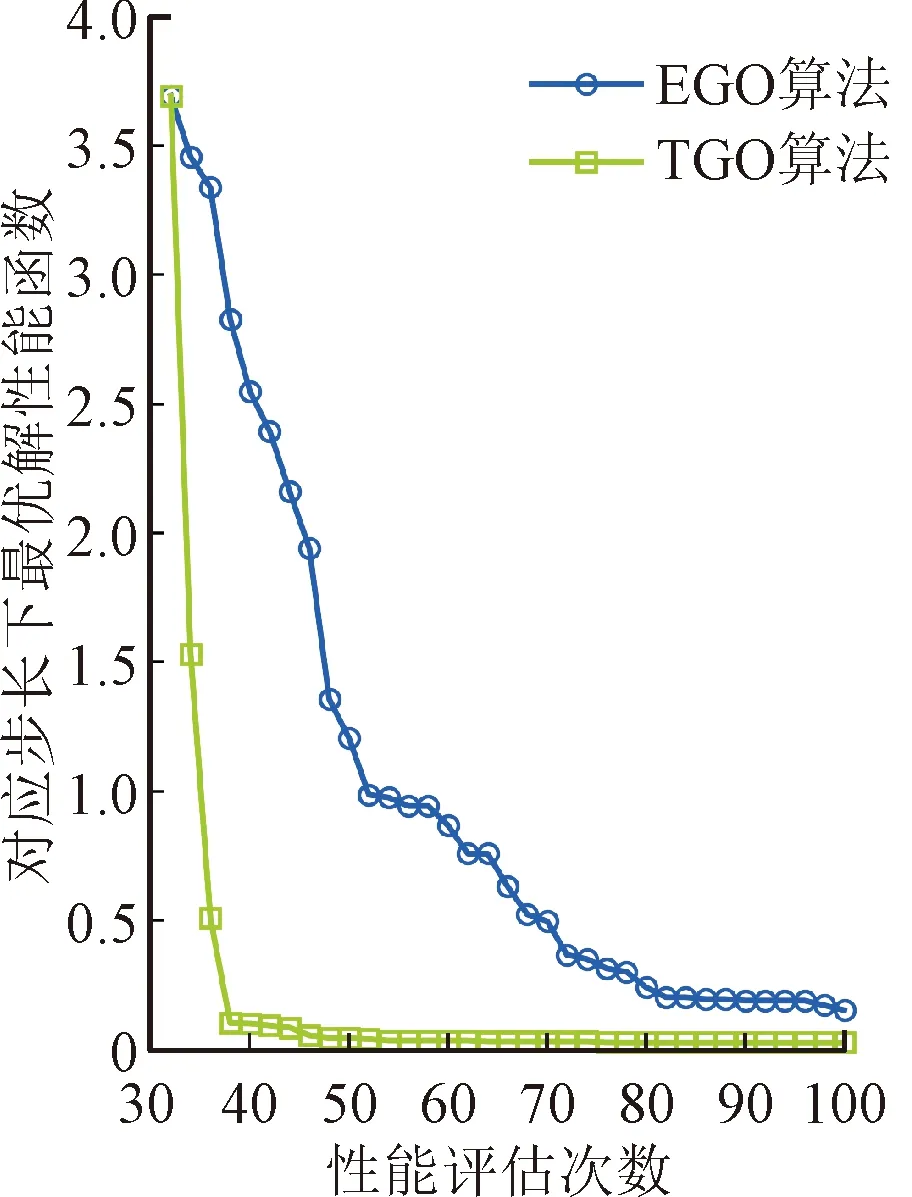
(a)基准函数1

(b)基准函数2

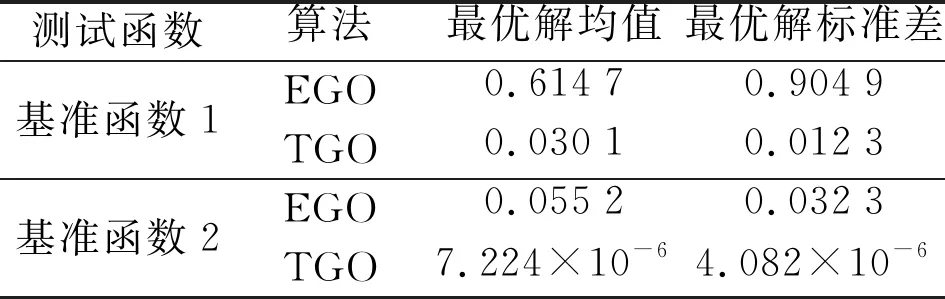
表3 2种算法的基准函数算例测试结果

2.3 采用知识迁移加速的设计优化框架VAE-TGO方法

将基于VAE的形状参数化方法与TGO算法相结合,研发了气动型线迁移优化框架,并将其命名为VAE-TGO方法,如图7所示。VAE-TGO方法的基本流程如下:首先收集型线样本,构建基于VAE的型线参数化模型;然后基于VAE解码器,在VAE低维参数化设计空间ζ进行样本采集,生成目标任务样本集{zT,yT}n。另一方面,基于VAE编码器,将以散点坐标表示的已完成任务样本{xS,yS}m编码至目标任务参数化设计空间,生成{zS,yS}m。上述过程又称为已完成任务样本重参数化,如图7中虚线框所示。最后进一步耦合{zT,yT}n和{zS,yS}m,基于TGO算法流场开展型线设计空间寻优。

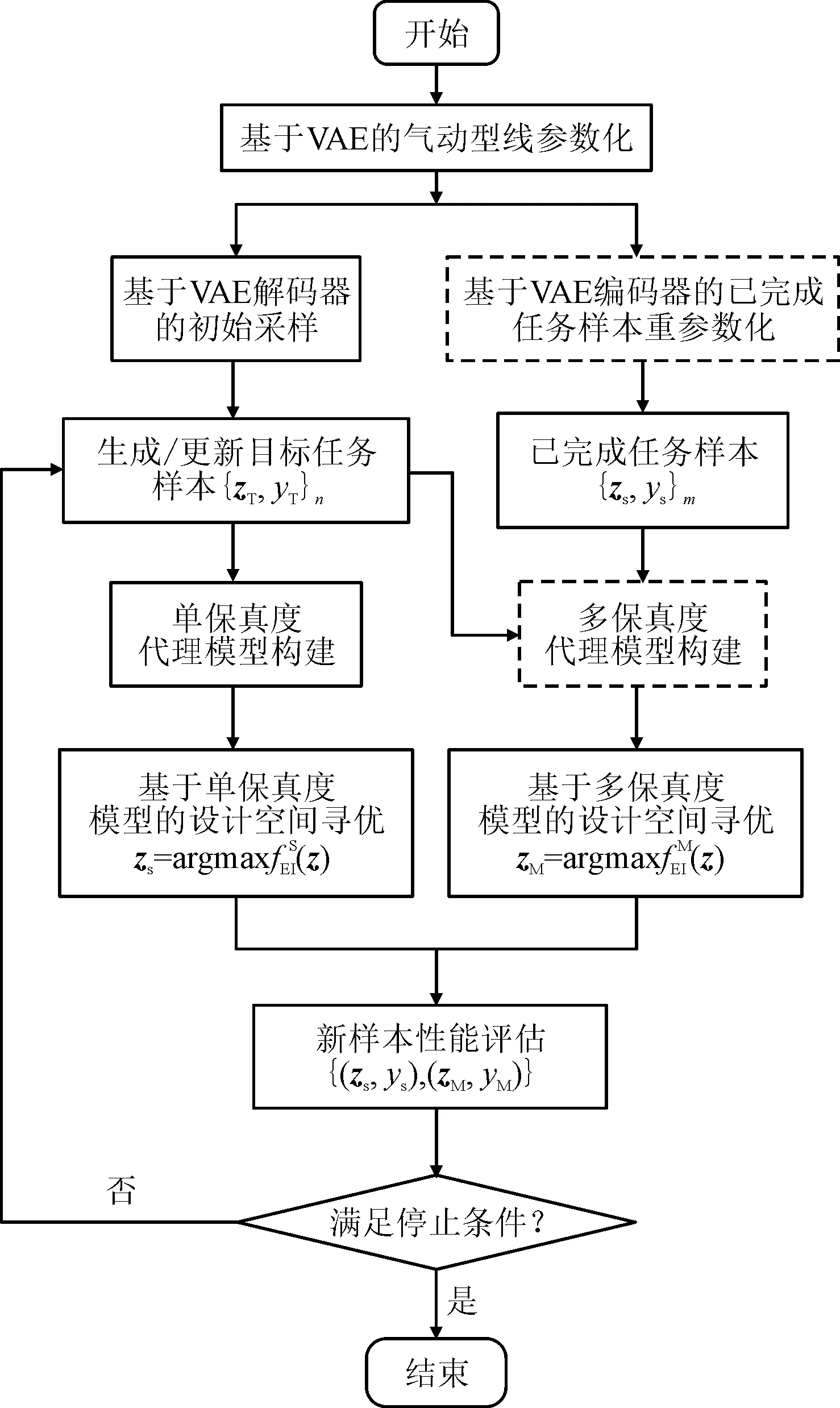
图7 VAE-TGO方法设计优化框架Fig.7 VAE-TGO design optimization framework

采用NURBS和FFD等传统参数化方法替代图7中的VAE参数化方法,可构建基于传统参数化方法的知识迁移优化框架,分别命名为NURBS-TGO和FFD-TGO法。但与VAE-TGO方法不同,NURBS-TGO和FFD-TGO方法难以将散点坐标表示的样本重参数化至目标任务参数化设计空间,因而NURBS-TGO和FFD-TGO方法仅在目标任务与已完成任务样本具有相同参数化设计空间的情形进行。

3 气动型线迁移优化典型案例测试

本节以跨声速翼型设计优化为例,对搭建的VAE-TGO方法的有效性进行验证。

3.1 目标优化问题及迁移源任务描述

参照相关研究工作[8,27],选取最大化翼型升阻比CL/CD(CL为升力系数,CD为阻力系数)为目标任务的优化目标函数,选取优化工况为Ma=0.75,Re=6.5×105,迎角α=0°。为满足结构强度要求,以RAE2822翼型作为参考设计,要求优化翼型截面积不小于参考面积的90%。对应的优化模型可表示为

(9)

式中:A(z)和ARAE2822分别为优化设计和参考设计的翼型截面积。

与此同时,用于知识迁移的已完成任务工况假定为Ma=0.45,Re=3.5×105,迎角α=0°。

3.2 优化过程相关设置

3.2.1 XFOIL性能评估求解器

选取广泛使用的XFOIL求解器,对优化过程中生成的翼型进行气动性能评估[28]。该软件理论基础为基于小扰动势流理论的面源法,以位于边界层位移厚度内流和外流的边界条件为迭代收敛的标志。由于XFOIL求解器对小攻角条件下的翼型扰流问题计算精度较高,被广泛应用于翼型设计优化性能的评估过程[8-9,29-30]。图8展示了RAE2822翼型在工况条件为Ma=0.676、Re=5.7×105、迎角α=2.4°下,XFOIL求解器的数值计算结果与文献 [28]中实验结果的对比。由图可见,XFOIL求解器得到的数值解与实验结果吻合良好,可满足优化设计过程中性能评估的精度要求。

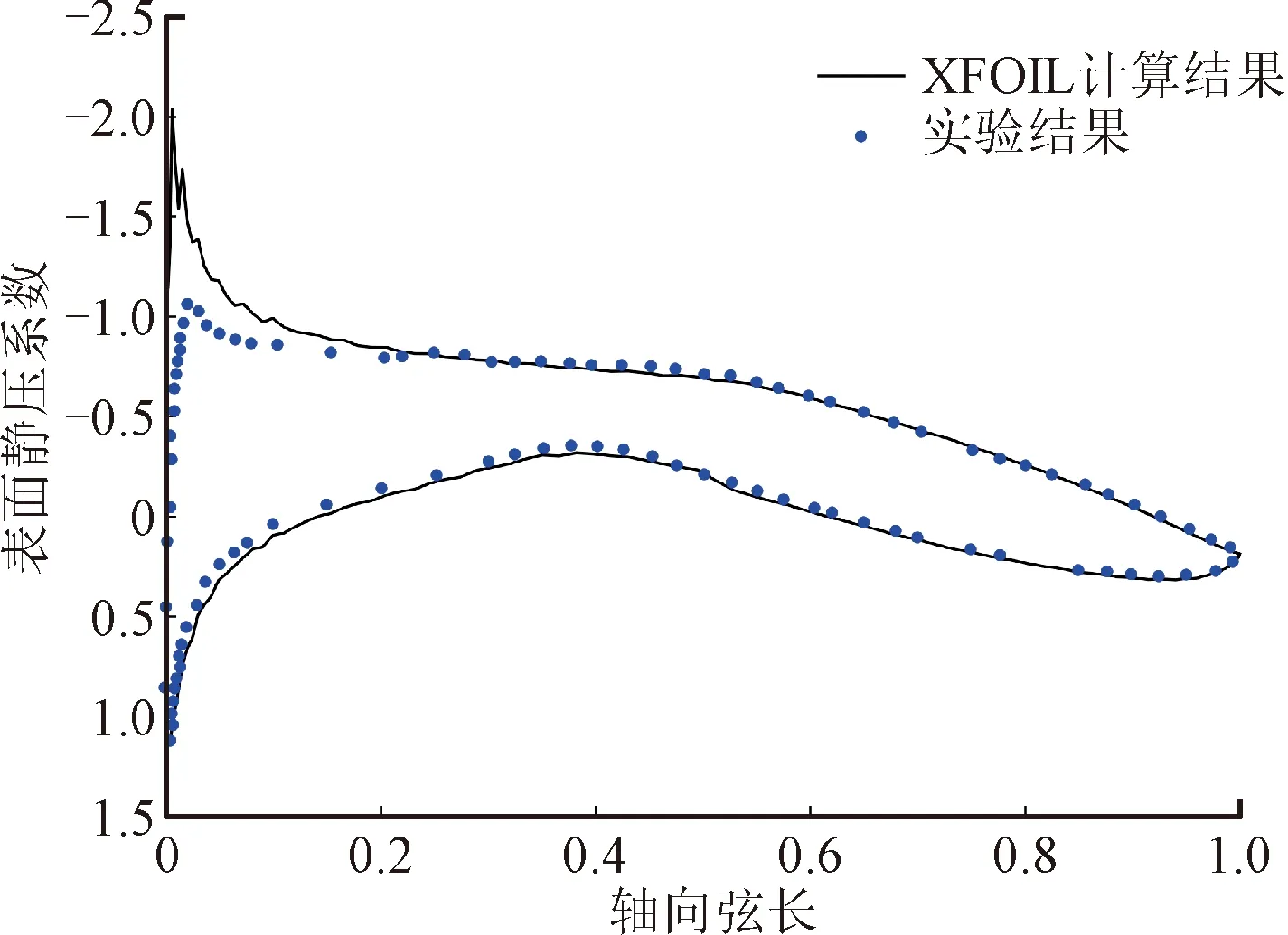
图8 XFOIL求解器计算结果与实验结果[28]对比Fig.8 Comparison of results of XFOIL and experimental data

3.2.2 优化方法相关设置

为验证知识迁移策略的有效性,分别采用知识迁移策略的优化方法与无知识迁移的传统优化方法求解式(9)所示的目标任务。除VAE参数化方法外,NURBS和FFD等传统方法亦被用于跨声速翼型参数化建模。其中,采用已完成任务样本进行知识迁移加速的优化过程被分别命名为VAE-TGO、NURBS-TGO和FFD-TGO方法,而不采用已完成任务样本进行知识迁移的传统优化过程则被命名为VAE-EGO、NURBS-EGO和FFD-EGO方法。

在进行翼型设计空间参数化建模时,VAE将以UIUC数据集作为训练样本集,VAE参数空间ζ的变量维度为10。NURBS和FFD参数化建模将以RAE2822翼型作为参考型线,参考陈伟等[8]相关工作完成NURBS与FFD方法的参数化空间设置。

注意到在已完成任务场景中,样本{xS,yS}m的分布特征依根据算法寻优过程而定,无法事先设置且不能人为更改。为模拟上述已完成任务场景,在参数化建模的基础上开展工况条件为Ma=0.45、Re=3.5×105、迎角α=0°的气动型线优化设计,所生成对应的优化样本将作为{xS,yS}m的候选样本集。为模拟已完成任务样本可能来自不同参数化空间的情形,从已完成任务优化解集中选取40个性能最优的个体{xS,yS}40,按照图7所示流程,采用VAE编码器对已完成任务样本重参数化,在获得目标参数空间样本{zS,yS}40后开展迁移优化。

与VAE-TGO方法不同,由于NURBS和FFD方法难以将散点坐标表示的型线样本编码至目标任务参数化设计空间,因而在采用NURBS和FFD方法完迁移源任务优化后,直接从已完成任务优化解集中选取性能最优的40个样本{zS,yS}40,用于NURBS-TGO和FFD-TGO方法的优化过程。

在EGO和TGO算法设置方面,相关参数设置与2.2.3节标准算例保持一致,即采用指数型高斯核函数分别构建单保真度和多保真度代理模型。同时,采用拉丁超立方抽样技术生成40个目标任务的初始样本,优化过程所允许的总样本评估次数设为140。

3.3 结果分析

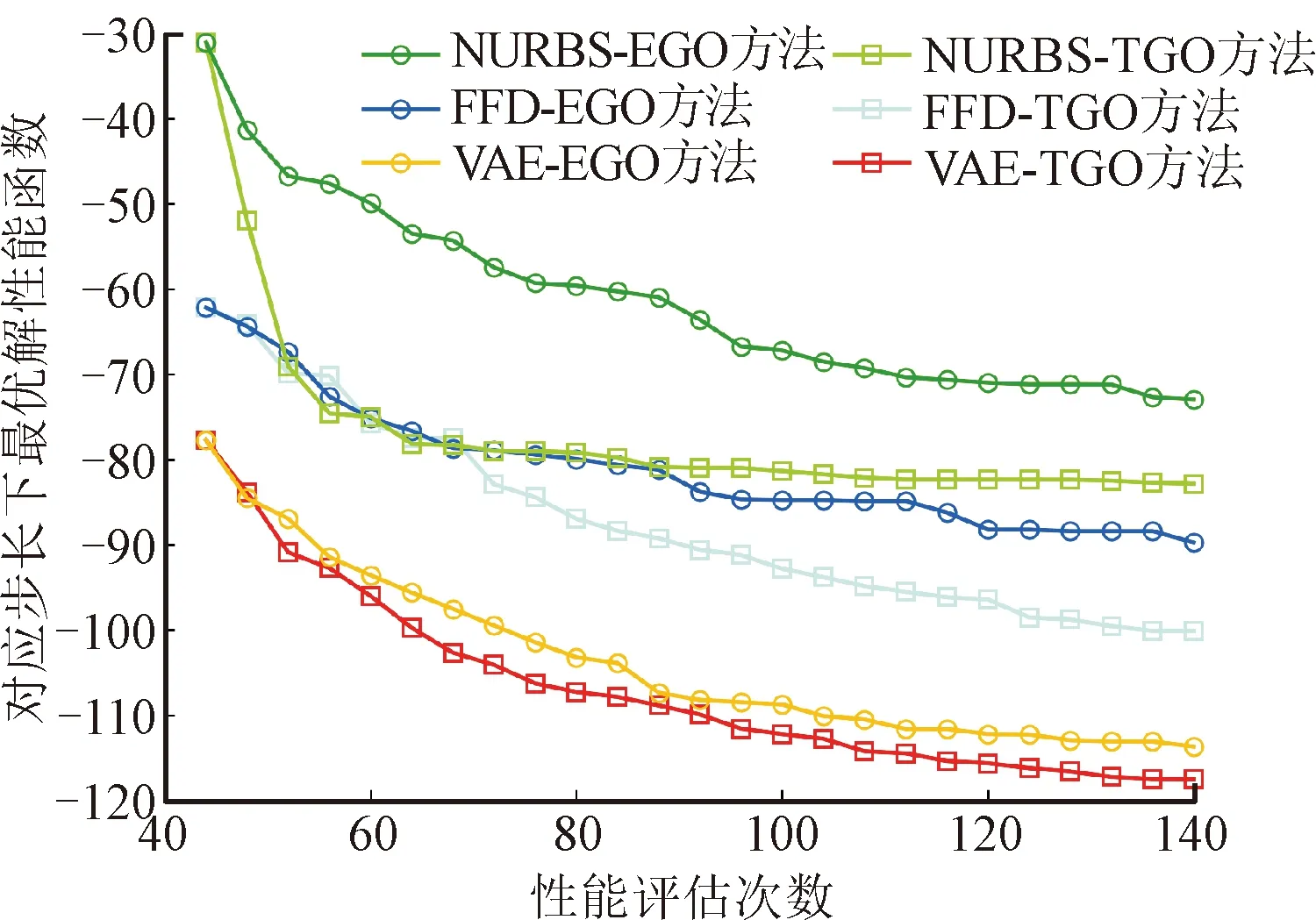
基于3.2节相关设置,采用VAE-TGO等不同优化方法,对独立抽取的初采样和迁移源样本开展10次优化,得到的优化结果如图9所示。由于采用拉丁超立方抽样技术所生成的目标任务初始样本的分布不同,因而10次优化所得到的最优解存在差异。图9(a)和(b)分别展示了10次优化平均结果收敛过程和所得到的最优解分布。

(a)平均优化结果收敛曲线

(b)最优解统计箱线图

相较而言,采用VAE方法的翼型优化结果在优化收敛速度和最优解性能方面均显著优于基于NURBS和FFD方法所得到的优化结果,这和李继超等[1]、陈伟等[8]获得的结果相类似。由于NURBS和FFD等传统参数化方法需先选定参考型线,所构建的参数空间型线样本形状往往需要对参考翼型进行小幅度调整,因而参数空间内性能优异的型线样本相对匮乏。相反地,基于VAE模型的参数化方法将囊括了从低速翼型到跨声速翼型等各式各类型线的UIUC数据库作为训练数据,且VAE深度学习模型的非线性特征捕捉能力强,可较好地捕捉数据库中各类翼型的几何特征,因而使得VAE参数空间样本多样性强,且所囊括的性能优异的型线样本更为丰富。因此,基于VAE方法的优化收敛曲线从初始阶段开始,所得到的最优解即显著优于FFD和NURBS方法的优化结果。

基于相同的参数化模型,将TGO方法的优化结果与无知识迁移的EGO方法的优化结果进行比较后可知,对于所采用的VAE、FFD、NURBS这3种参数化方法,TGO方法的优化过程在优化进程和取得最优解两个方面均明显优于无知识迁移的EGO方法的优化过程。由此表明,本文提出的多保真度迁移优化策略与多平台迁移优化策略能有效提取已完成任务优化解集中有用的设计信息,从而显著提高目标任务的求解速度与最优解性能。

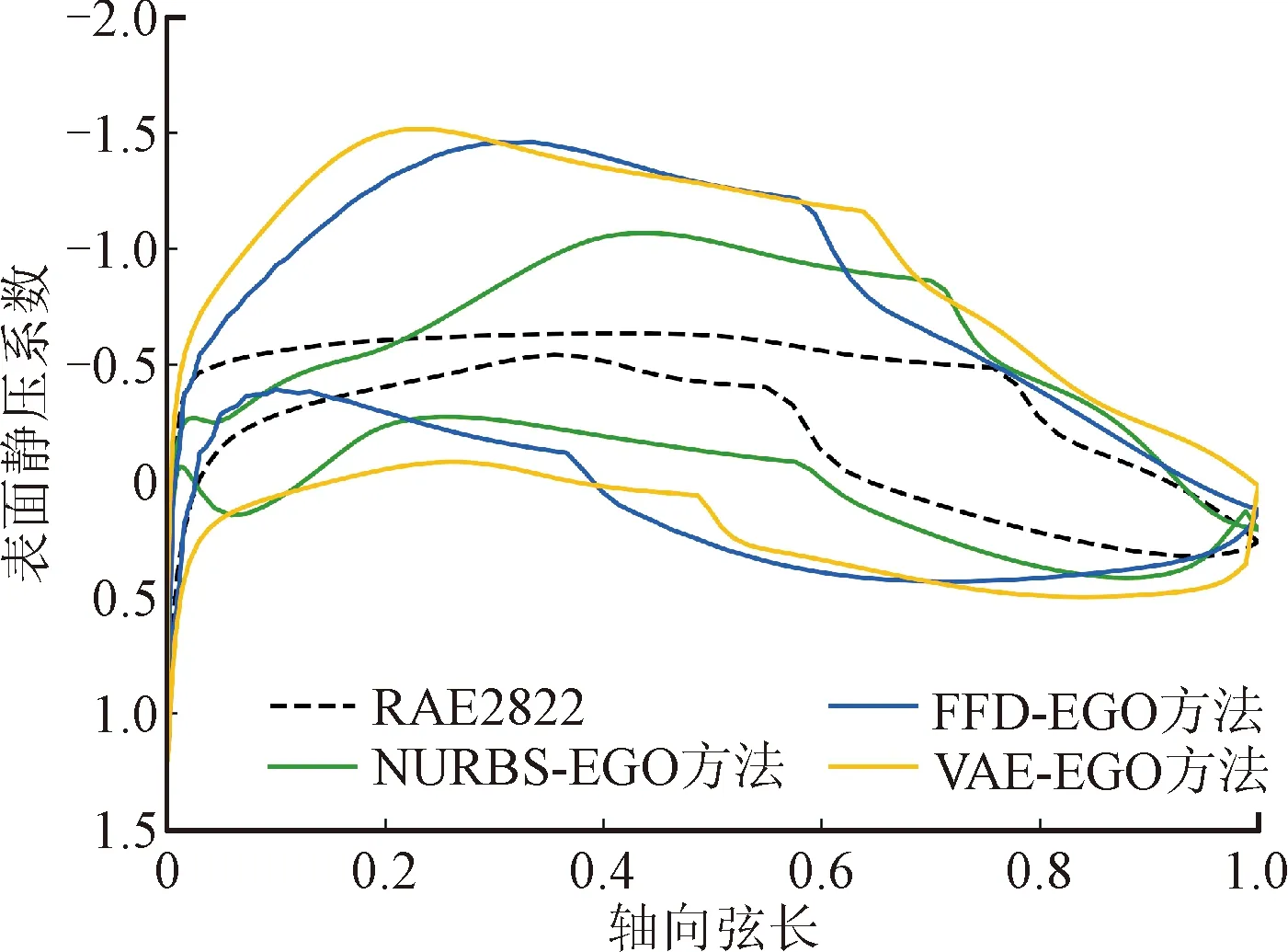
在进一步探究采用知识迁移策略的有效性之前,以最优解集中的中位数作为代表,对采用不同优化方法所得到的最优型线进行气动分析。图10展示了RAE翼型和中位数解所对应的气动型线。由图可见,相较于RAE2822翼型,优化后的翼型弯曲程度明显增加,靠近尾缘的区域曲线上凹趋势最为明显,此区域型线的变化有利于在吸力面增大气流速度、降低当地静压,在压力面降低气流速度且提高当地静压,从而达到显著提升翼型升力的目的。表4给出了不同设计方法得到的最优设计性能对比,可见相较于RAE2822翼型,优化后翼型的升力系数和升阻比均显著增加,但优化翼型阻力系数却略有增加,这与式(9)所选取的目标函数有关。在未来的优化研究中,加入关于阻力系数的约束条件有望解决上述不足。

(a)RAE2822

(b)NURBS-EGO

(c)FFD-EGO

(d)VAE-EGO

(e)NURBS-TGO

(f)FFD-TGO

(g)VAE-TGO

图11进一步展示了不同翼型表面的压力系数分布。由图可见,相较于RAE2822翼型,优化后翼型的载荷明显提升,这与表4中各优化解所对应的升力系数显著提升的结果吻合较好。与此同时,从各优化翼型表面压力系数分布易见,翼型表面流动组织良好,没有出现大迎角和大分离的情况,表明优化后的翼型气动性能良好。

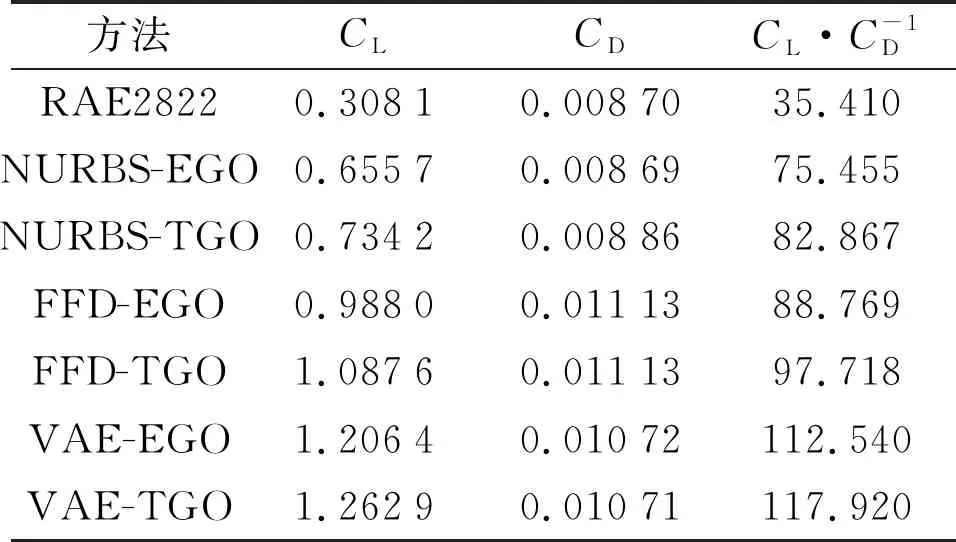
表4 不同设计方法得到的最优设计性能对比

(a)未使用知识迁移策略

(b)使用知识迁移策略

3.4 迁移优化机理讨论

在验证优化解性能有效性的基础上,本节对知识迁移可加速目标任务优化进程的原因进行了探究。采用VAE参数化模型生成1 024个型线样本,分别计算已完成任务工况和目标任务工况下同一翼型的升阻比,并对其进行相关性分析,得到的结果如图12所示。由图可见,皮尔逊相关系数为0.911 0,表明对于Ma=0.75的目标任务工况与Ma=0.4的已完成任务工况,翼型表面流动存在一定的相似性,这与描述亚声速翼型流动相似性的普朗特-葛劳渥法则吻合较好[31],即在迎角不变的情况下,不同工况下翼型的表面静压系数分布可近似地按来流马赫数的单值函数缩放。这一流动相似性法从理论上佐证了已完成任务与目标任务间的相关性。

图12 同一翼型不同工况下的性能指标相关性Fig.12 Correlation between performances of identical airfoil under different working conditions

在验证目标优化任务与已完成任务流动相似性的基础上,对采用知识迁移可加速目标任务优化进程的机理可作如下解释:一方面,在目标任务与已完成任务相似性较高的前提下,将已完成任务样本与目标任务样本耦合后构建多保真度代理模型,可有效提高用于捕捉设计空间全局趋势的代理模型精度,进而加速目标任务的求解;另一方面,已完成任务与目标任务流动的相似性表明,已完成任务与目标任务的最优解分布在设计空间相同的邻域。因此,将已完成任务样本加入到目标任务建模与求解过程中,可帮助优化求解器更快地到达目标任务最优解邻域,从而加速目标任务优化进程。

4 结 论

受机器学习领域迁移学习理念的启发,将深度学习模型VAE和贝叶斯优化算法相结合,采用知识迁移加速研发了智能气动形状设计优化方法,主要获得以下结论。

(1) 相对于NURBS、FFD等传统参数化方法,采用VAE方法所构建的翼型参数化设计空间样本的多样性更强,表明基于VAE方法的优化设计结果显著优于基于传统参数化方法所获得的优化解。此外,VAE编码器结构可将采用不同参数化方法建模的已完成任务样本编码至相同的参数化设计空间,为拓展迁移优化方法在气动形状设计领域的应用提供契机。

(2) 数值算例与翼型气动型线优化的分析结果表明,将多保真度建模的序列迁移策略与多平台迁移优化策略相结合,可充分挖掘已完成任务样本中所包含的有用设计信息,从而显著加速目标任务优化进程,得到的最优解性能明显优于无知识迁移的传统优化方法优化解。

为验证知识迁移策略的有效性,本文主要针对翼型的气动性能展开优化设计,但该方法可通用于考虑结构强度约束的翼型多学科设计优化问题,并可推广至航空发动机叶片二维及三维多学科设计优化。