基于增材制造旋转直驱伺服阀的肢腿运动单元位置控制研究

方李舟, 张军辉, 纵怀志, 张 堃, 杨郅贤, 徐 兵

(浙江大学 流体动力与机电系统国家重点实验室, 浙江 杭州 310027)

引言

移动机器人因为其良好的环境适应性、空间探索性能并且其不需要人工进行操作的自主性,在近30年的研究中备受关注。移动机器人主要包括轮式机器人、履带式机器人和腿式机器人。其中腿式机器人的研究在过去几十年中不断进步与完善,因为腿式机器人相比于其他移动机器人具有更出色的运动能力与灵活性,能在复杂地形更高速高效的完成运动。四足机器人是腿式机器人中运动机动性与稳定性的最佳选择[1]。

由液压驱动的四足机器人相较于由电机驱动的四足机器人具有更好的动态特性、更高的移动速度与更高的负载能力[2]。目前最具代表性的液压驱动四足机器人是美国波士顿动力公司(Boston Dynamics)的BigDog[3],WildCat[4]和Spot[5]机器人和意大利技术研究院(Italian Institute of Technology, IIT)的HyQ系列四足机器人[6]。在液压四足机器人中,电液伺服控制系统尤为重要,其决定着四足机器人的控制精度与运动稳定性[7]。而电液伺服阀在系统中很大程度上决定了整个系统的性能,目前应用最广泛的电液伺服阀为喷嘴挡板式电液伺服阀[8],这种原理的电液伺服阀拥有较高的精度与较快的响应速度,但是无功损耗大,抗污染能力差。除喷嘴挡板式电液伺服阀外,其他的新型电液伺服阀驱动方式中最具特点的是旋转直驱式伺服阀[9]与旋转阀芯的新型伺服阀[10],其能够在达到高响应高精度的同时,提高电液伺服阀的抗污染性能[11]。目前的液压驱动四足机器人中,大多数国内研究团队使用MOOG公司设计的喷嘴挡板式电液伺服阀[12-17],而美国波士顿动力公司最新设计的液压机器人大多使用的为旋转直驱式伺服阀,同时在液压双足机器人Altas中使用了定制的特殊结构电液伺服阀[18]。

为了探究旋转直驱伺服阀与喷嘴挡板式伺服阀在肢腿单元位置控制中的优劣,本研究以液压四足机器人系统中的电液伺服阀为研究对象,研究不同原理的电液伺服阀对于液压四足机器人肢腿单元的位置控制的影响。首先建立了喷嘴挡板式与旋转直驱式伺服阀的数学模型,并对基于两种电液伺服阀的阀控缸PID位置控制动态性能进行了仿真对比分析。最后在本团队设计的液压四足机器人肢腿单元实验台上进行了实验验证。

1 数学模型

喷嘴挡板电液伺服阀与旋转直驱式电液伺服阀最大区别为两种阀的动态特性的差异。针对这两种电液伺服阀进行数学建模,并对这两种模型进行了对比分析。

1.1 喷嘴挡板电液伺服阀数学模型

二级双喷嘴挡板电液伺服阀的基本结构组成如图1所示。其中先导级液压放大器为双喷嘴挡板阀,由永磁动铁式力矩马达控制,主级为四通滑阀,阀芯位移通过反馈杆与衔铁挡板组件相连,构成滑阀位移力反馈回路。当有差动控制电流Δi=i1-i2输入时,衔铁上产生逆时针方向的电磁力矩,使衔铁档板组件绕弹簧转动中心沿逆时针发生偏转,使挡板偏离中位。此时滑阀左右腔控制压力差推动滑阀阀芯左移,带动反馈杆顶端小球左移,直到反馈杆反馈力矩、喷嘴挡板的液压力矩和输入电流信号产生电磁力矩相平衡时,阀芯将停止运动,其位移与控制电流成比例。输入的电流越大衔铁的转矩越大,则挡板偏离中位的位移xz以及阀芯的偏移量xv越大,电液伺服阀输出的流量也越大。p1,p2为进出口压力,ps为供油压力。

1.永久磁铁、导磁体 2.衔铁 3.线圈 4.反馈杆 5.喷嘴挡板 6.阀芯图1 喷嘴挡板式电液伺服阀原理图Fig.1 Schematic diagram of nozzle baffle electro-hydraulic servo valve

根据喷嘴挡板阀的原理分析,对其进行数学建模。

力矩马达的推挽工作时,线圈的电压信号为:

u1=u2=Kuug

(1)

式中,u1,u2—— 线圈的信号电压

Ku—— 每侧放大器的增益

ug—— 输入放大器的信号电压

有线圈回路中的电压平衡方程如下:

(2)

(3)

式中,Eb—— 产生常值电流所需的电压

Zb—— 线圈公用的阻抗

Rc—— 每个线圈的电阻

rp—— 每个线圈回路中的放大器内阻

Nc—— 每个线圈的匝数

φa—— 衔铁磁通

衔铁磁通表达式为:

(4)

将式(2)与式(3)相减,代入Δi=i1-i2、式(1)与式(4)可得:

(5)

拉氏变换后可改写为:

(6)

力矩马达输出的电磁力矩:

Td=KtΔi+Kmθ

(7)

衔铁挡板组件的运动方程:

(8)

式中,Ja—— 衔铁挡板组件的转动惯量

Ba—— 黏性阻尼系数

Ka—— 弹簧管刚度

TL1—— 喷嘴对挡板的液流力产生的负载力矩

TL2—— 反馈杆对衔铁挡板组件产生的负载力矩

这两个力矩的表达式为:

(9)

式中,AN—— 喷嘴口的面积

pLP—— 两个喷嘴腔的负载压差

r—— 喷嘴中心至弹簧管回转中心的距离

Cdf—— 喷嘴与挡板之间的流量系数

xf0—— 零位间隙

b—— 反馈杆小球中心到喷嘴中心的距离

Kf—— 反馈杆刚度

xv—— 阀芯位移

将式(7)～式(9)联立后拉氏变换,可改写为:

(10)

挡板位置与衔铁转角的关系:

Xf=rθ

(11)

喷嘴挡板至滑阀的传递函数:

(12)

阀控缸的传递函数:

(13)

挡板上的压力反馈:

(14)

滑阀负载压力:

(15)

在一般情况下力矩马达的控制圈数的动态和滑阀的动态可以被忽略,且作用在挡板上的压力反馈的影响比反馈力小,故压力反馈回路也可忽略。综合上述式子可以得到简化过的喷嘴挡板式电液伺服阀传递函数为:

(16)

其中,Ksv为伺服阀的流量增益:

(17)

由于在液压四足机器人的阀控缸系统中,伺服阀的动态响应高于动力元件的动态响应,所以传递函数能够简化为二阶震荡环节:

(18)

式中,ωsv—— 伺服阀的固有频率

ζsv—— 伺服阀的阻尼比

由式(16)计算得到的相频特性曲线中取相位滞后90°所对应频率为ωsv。阻尼比ζsv可由二阶环节的相频特性公式求得。

1.2 旋转直驱式电液伺服阀数学模型

旋转直驱伺服阀由有限转角电机、电机滑阀位移转换副与功率滑阀这几个部分组成,如图2所示为一款增材制造的旋转直驱电液伺服阀的原理图。旋转直驱阀采用有限转角电机,再利用位移转换副将电机的旋转运动转换为阀芯的水平运动与绕轴线的转动,水平运动控制伺服阀的输出压力,转动为了避免运动干涉。图中的旋转直驱式电液伺服阀使用的是小球-柱形孔运动副来实现运动的转换。

1.功率滑阀 2.位移转换副 3.有限转角电机图2 旋转直驱式电液伺服阀原理图Fig.2 Schematic diagram of rotary direct drive electro-hydraulic servo valve

根据小球柱形孔旋转直驱式电液伺服阀的原理分析,对其进行数学建模:

有限转角电机的转子动力学方程:

(19)

式中,Jr—— 电机转动惯量

α—— 电机转角

Tem—— 电机输出力矩

Br—— 转动阻尼

TL—— 负载力矩

其中的电磁力矩Tem与转角α据实验可得其关系曲线能够采用二阶函数模型进行拟合:

Tem=kti0-kmα2

(20)

式中,kt,km—— 电流-力矩系数与转角力矩系数

i0—— 转角电机的输入电流

在电机转角较小时,输入电流与输出力矩呈近似线性关系:

Tem=kti0

(21)

小球-柱形孔运动转换的运动转换主要靠机构中的两处偏心完成,分别是小球球心偏离电机轴线e0和小球球心偏离阀芯轴线h0。此机构将有限转角电机的转动转换为阀芯的水平运动xv与绕轴线的转动βv。此机构的运动学方程如下:

(22)

式中,αx—— 任意位置电机角度

kβv—— 阀芯绕轴线的转角变化系数

电机在此转换机构中所受到的阻力矩为:

(23)

式中,Fx—— 小球对阀芯水平移动方向的作用力

Tβ—— 小球对阀芯绕轴线转动的力矩

稳态液动力与滑阀开度有关,可将其视为弹性力,于是有:

(24)

正开口滑阀所受驱动力和驱动力矩的表达式为:

(25)

将式(20)～式(25)代入式(19)中得到等效在电机转子上的输出力矩与电机转角的关系式:

(26)

综合上述式子可以得到旋转直驱伺服阀的传递函数:

(27)

其中:

(28)

1.3 对比分析

根据1.1节与1.2节的数学模型建立可以得到,两种不同原理的电液伺服阀的传递函数都为二阶传递函数,由于不同的驱动原理导致了两种不同的电液伺服阀的固有频率、阻尼比和压力流量增益系数不同,从而导致两种电液伺服阀拥有不同的动态响应性能。

2 仿真分析

根据上述两种不同原理的电液伺服阀的传递函数进行仿真分析。在AMESim中搭建了如图3所示的阀控缸模型。该模型为简单的PID阀控缸位置控制模型,其中的伺服阀模块使用的是拥有二阶系统模型的伺服阀模块,更改模块中的伺服阀的固有频率和伺服阀阻尼比两个参数以及更改两种阀的流量压力特性即可在仿真中体现出两种阀的差异情况。仿真中的阀控缸模型参数与实验平台的参数保持一致。

图3 AMESim阀控缸PID位置控制模型Fig.3 AMESim valve control cylinder PID position control model

仿真1:使用此模型对两种阀在阀控缸系统中的PID位置控制阶跃响应性能进行了仿真。阶跃响应输出模块在1 s的时间输出了一个0.046的阶跃信号,表示控制液压缸运动到0.046 m的长度,此取值由机器人对应步长所确定。在仿真进行前,将两组阀控缸系统的PID参数调整为与其对应的不同的两组参数。仿真得到了如图4所示的结果,旋转直驱式电液伺服阀的阀控缸系统阶跃响应时间为104 ms,喷嘴挡板式电液伺服阀的阀控缸系统阶跃响应时间为124 ms,旋转直驱式电液伺服阀比喷嘴挡板式电液伺服阀阶跃响应时间减少了16.12%。

图4 阀控缸PID位置控制阶跃响应结果Fig.4 Step response result of model

仿真2:使用此模型对两种阀在阀控缸系统中的PID位置控制液压缸末端正弦轨迹响应进行了仿真。正弦输出模块输出平均值为0.03幅值为0.025的正弦信号,仿真分别采用了1, 1.5, 2, 2.5 Hz的4种不同频率的正弦信号。仿真得到了如图5所示的结果,旋转直驱式电液伺服阀的液压缸末端正弦轨迹跟踪误差为9.45°,喷嘴挡板式电液伺服阀的正弦信号跟随误差为12.6°,旋转直驱式电液伺服阀比喷嘴挡板式液压缸末端正弦轨迹响应时间减少了25%。

3 实验验证与分析

为了探究旋转直驱式电液伺服阀能给液压四足机器人肢腿单元的位置控制带来的实际优势,对旋转直驱式电液伺服阀以及喷嘴挡板式电液伺服阀在液压四足机器人肢腿单元上的位置控制性能进行实验对比。本团队搭建了具有髋关节屈伸及膝关节屈伸两自由度的液压四足机器人肢腿单元实验平台。实验台液压系统的原理图如图6所示。本次实验中的高压油源压力设定为14 MPa。

1.油箱 2.过滤器 3.温度计 4.电机 5.液压泵 6.溢流阀 7.压力传感器 8.压力表 9.单向阀 10.流量计 11.旋转直驱伺服阀 12.液压缸图6 实验平台原理图Fig.6 Schematic diagram of experimental platform

实验使用的旋转直驱电液伺服阀与喷嘴挡板电液伺服阀分别为:Domin S4 PRO旋转直驱电液伺服阀与航宇智星HY(F)110喷嘴挡板电液伺服阀,两款电液伺服阀的相关参数如表1所示。实验台中肢腿单元液压执行器使用的为本团队设计的通过碳纤维加强层进行轻量化改进的液压缸。髋关节与膝关节处使用的是单圈CAN通信角度编码器读取关节旋转角度。实验台使用的控制器由能过够读取编码器的CAN通信信号,并且能够给两种电液伺服阀发送对应的模拟电流信号。控制器的程序设计是基于模型(MBD)的设计方式,通过MATLAB的Simulink功能中的TI公司的C2000硬件支持包来实现。实验使用其中的外部仿真模式用于实现肢腿单元实时控制以及实时数据信号的采集。图7为肢腿单元实验台的实物图,控制器从肢腿单元编码器中读取关节角度返回给控制器,再由控制器输出控制信号给电液伺服阀。

表1 电液伺服阀相关参数Tab.1 Parameters of electro-hydraulic servo valve

图7 实验平台Fig.7 Experimental platform

实验1:对肢腿单元膝关节进行基于位置控制阶跃响应实验,实验工况为膝关节角度由0°摆动至60°,阶跃信号在100 ms时触发对照内容为两款不同原理的电液伺服阀,经过Simulink中的外部仿真模式的示波器后得到结果如图8所示。旋转直驱电液伺服阀控制的膝关节摆动阶跃响应时间为134.084 ms,喷嘴挡板电液伺服阀控制的膝关节摆动阶跃响应时间为155.975 ms,旋转直驱式电液伺服阀比喷嘴挡板式电液伺服阀阶跃响应时间减少了14.03%。

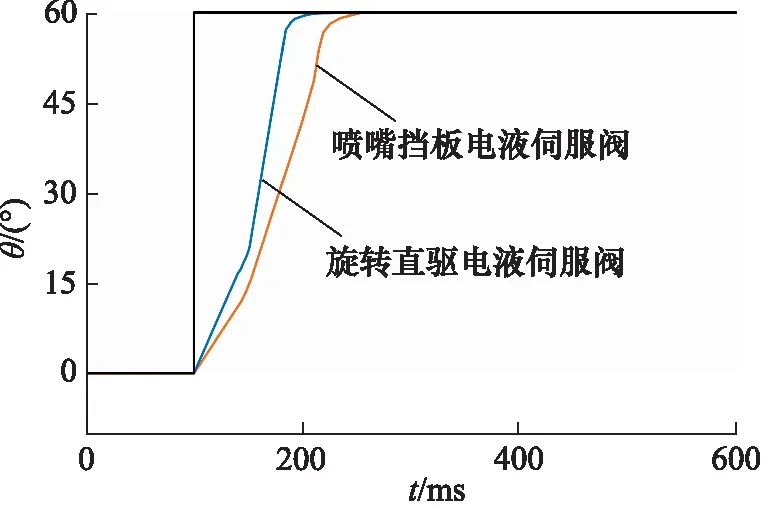
图8 阶跃响应实验结果Fig.8 Result of step response test

实验2:对肢腿单元进行基于位置控制的膝关节足端正弦轨迹跟踪响应实验,实验工况为膝关节角度由40°为起始角度进行幅值为30°的正弦信号运动,取正弦信号频率为1, 1.5, 2, 2.5 Hz 4个不同的工况。得到的实验结果如图9所示,分别表示了4个不同工况下的实验数据,通过对比足端正弦轨迹跟踪误差来说明两种电液伺服阀的在液压四足机器人位置控制中的动态性能差异。这4种工况下的实验结果如表2所示,旋转直驱电液伺服阀比喷嘴挡板式电液伺服阀的足端正弦轨迹跟踪误差减少了21.61%。

表2 正弦信号足端轨迹跟踪实验结果Tab.2 Result of sine signal following test

图9 正弦信号跟随实验结果Fig.9 Results of sinusoidal signal follows experiment

4 结论

本研究针对在液压四足机器人系统中的两类不同原理的电液伺服阀:旋转直驱式电液伺服阀与喷嘴挡板式电液伺服阀进行研究,首先根据两种电液伺服阀的控制原理进行了数学模型的构建,得到了两种电液伺服阀的传递函数,分析了两种阀的频率响应特性。利用得到的数学模型在AMESim仿真软件中测试了两种阀在PID位置控制下的动态性能与阶跃响应性能,结果表明旋转直驱式电液伺服阀拥有更好的动态性能,阶跃响应时间减少了16.12%,足端正弦轨迹跟踪误差减少了25%。在本团队设计的液压四足机器人肢腿单元实验平台上对这两种阀进行了实验验证,实验表明,在相同的流量压力需求下,应用旋转直驱阀的控制系统足端阶跃响应时间减少了14.03%,足端正弦轨迹跟踪误差减少了21.61%。