海浪扰动下电液3-UPS/S舰船并联稳定平台振动特性分析
2023-10-28袁晓明王维锜张睿聪周如林张立杰
袁晓明, 王维锜, 张睿聪, 周如林, 张立杰
(1. 燕山大学 河北省重型机械流体动力传输与控制实验室, 河北 秦皇岛 066004; 2.北京天玛智控科技股份有限公司, 北京 101399)
引言
舰船在海上行驶过程中,海浪激励是舰船摇摆运动的主要因素[1]。对于随机海浪运动规律的分析,主要有切片理论[2-3]和谱分析法[4-5]两种方法。切片理论以空气动力学的细长体概念为基础,在1955年被用于解决船舶摇摆问题[6],成为计算船舶纵摇运动的理论起点;谱分析法以海浪频谱与方向谱为基础,多用于随机海浪造型演示[7-8]、海浪运动模拟平台研发[9-10]等领域。
为了隔绝船舶运动对船舶设备的影响,通常使用舰船稳定平台补偿船舶的运动,维持设备在惯性空间内的相对稳定[11-13]。依据机构类型分类,舰船稳定平台可分为串联稳定平台和并联稳定平台两种[14]。相对串联稳定平台,并联稳定平台以承载能力强、易于实现多轴耦合驱动等优点,在高精度作业场合具有广泛的应用前景[15]。
为进一步提高稳定平台的性能,通常采用具有响应速度快,累计误差小等优点的电液驱动形式[16-18]。但是流体工作介质引入导致的机液耦合作用[19-20]、机械构件的间隙与局部刚度带来的非线性特征[21]、稳定平台工作过程中的姿态变化[22]等因素使机构的振动特性更为复杂,严重制约了稳定平台的补偿与控制精度的提升[23]。当平台在复杂海况下运行时,可能出现外部激励接近稳定平台固有频率的情况,严重时甚至可能导致设备的损坏[24],因此研究电液驱动的舰船并联稳定平台振动特性具有重要意义。但是在研究电液驱动的舰船并联稳定平台振动特性问题时,大多数学者建立动力学方程时通常忽略铰链刚度的影响,对随机海浪激励条件下机构固有频率变化规律的研究也尚未开展。
因此,以电液3-UPS/S舰船并联稳定平台为研究对象,在考虑铰链刚度的基础上利用虚功原理建立机构的动力学方程。以6级海况下机构的姿态补偿运动曲线作为输入,分析了机构固有频率的变化特性,以及机构固有频率在连续变化工作空间内随位姿的变化规律。本研究可为揭示电液驱动的并联稳定平台振动的振动机理提供一定的理论基础。
1 海浪扰动激励下船舶运动规律分析
1.1 海浪运动描述
通常在工程中考虑的海浪为充分发展的海浪,因此基于海浪随机理论,海浪被认为是长峰不规则波,即传播方向单一,波峰线很长且相互平行。依据线性波理论,长峰不规则波可以被简化为无限个不同波长、不同波幅、随机初相位的单元规则波线性叠加组成,其数学表达式如式(1)所示:
(1)
式中,ζn—— 第n项组成波的波幅
kn—— 第n项组成波的波数
x—— 第n项自由度方向上的坐标
ωn—— 第n项组成波的频率
εn—— 第n项组成波的随机相位
实际海浪的运动过程可以看作是海浪的能量传递过程,因此为了描述海浪的统计特性引入了“能量谱”的概念。海浪的“能量谱”也被称为海浪谱,描述了海浪的能量与各组成波的分布关系。现在常用的海浪谱多为半经验半理论公式,为适应我国海域的海浪特点,我国海洋局也提出了适合我国海域的海浪谱函数,表达式如式(2)所示[25-26]:
(2)
式中,g—— 重力加速度
ωh—— 海浪波的频率
U1—— 风速
1.2 船舶运动方程建立
在实际中,船舶受到海浪激励而产生的运动是十分复杂的,同时受到自然环境、船体结构的影响,因此本研究对船舶运动数学方程的推导是基于以下三点假设:
(1) 船体是刚体,即在运动和受力时不发生弹性变形;
(2) 船体的运动可以使用线性叠加原理进行求解;
(3) 海浪为理想流体,不可压缩,忽略其表面张力和流体黏性。
如图1所示,分别建立固连于船舶的动坐标系O-xyz和固连于大地的惯性参考系G-XYZ,由假设(1)可知,船舶的运动可在动坐标系O-xyz中由6个相互独立的空间坐标表示。
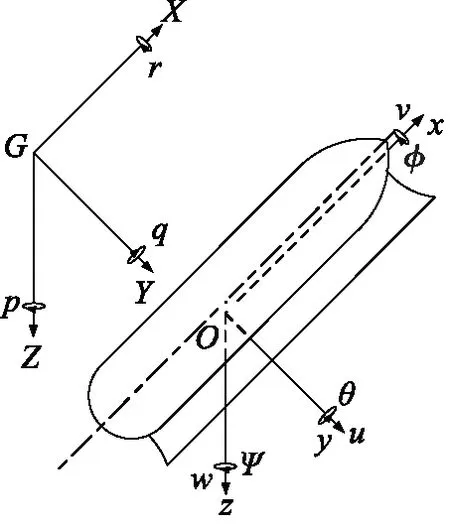
图1 船体运动描述坐标系Fig.1 Description frame of hull motion
由假设(2)可知,船舶的复杂运动可分解为各空间坐标方向上的运动,依据微幅波理论,船舶在各空间坐标方向上的运动方程类似,可统一表示为如下形式:
(3)
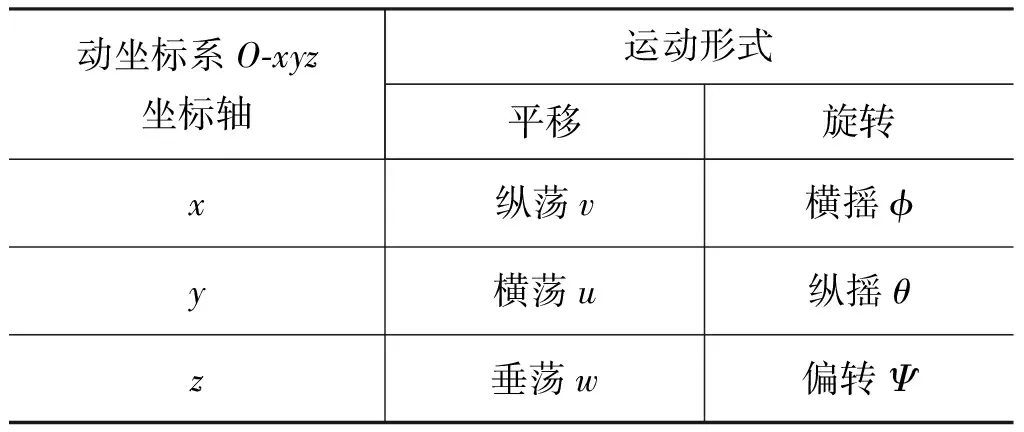
表1 表征船舶运动的物理参数Tab.1 Physical parameters of ship motion
式中,Y(t) —— 船舶在海浪激励下的运动响应
X(t) —— 海浪运动函数
χ—— 修正系数
c—— 衰减系数
ωc—— 船舶运动固有频率
若船舶受到规则的波浪作用,则波浪的波面角方程可以拟合为正弦函数,则其复数形式为:
x(t)=Imx0ejωht
(4)
式中, Im —— 复数的虚部
j—— 虚数单位
船舶自身为一个二阶线性系统,则其响应也为简谐运动,因此设式(3)特解如式(5)所示:
y(t)=Imy0ej(ωht+ε0)
(5)
式中,ε0为船舶运动与波面角的位相差。
将式(4)、式(5)代入式(3),并去掉虚部,可得:
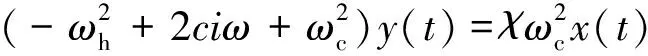
(6)
由式(6)可得船舶运动的频响函数为:
(7)
类比不规则海浪的简化过程,船舶的运动也可以表示为无数个规则海浪激励下的船舶运动的线性叠加。当船舶以一定航速和航向行驶时,遇到海浪时将会形成随机海浪遭遇波能谱,其表达式为:
(8)
式中,Sx(ωe) —— 遭遇频率的波能谱函数
Sζ(ωh) —— 海浪谱函数,选取式(2)
ωe—— 遭遇频率
v1—— 船舶航速
σ—— 船舶航向角
则船舶运动的能谱密度函数与遭遇频率的波能谱密度函数之间的关系为:
Sy(ωe)=|W(jωe)|2Sx(ωe)
(9)
为得到船舶在某段时间的运动样本,参照随机海浪模拟的方式,在船舶运动的谱空间内以Δω为间隔进行随机抽样,Δω的选取原则如表2所示,最终得到船舶运动响应解析表达式如下:
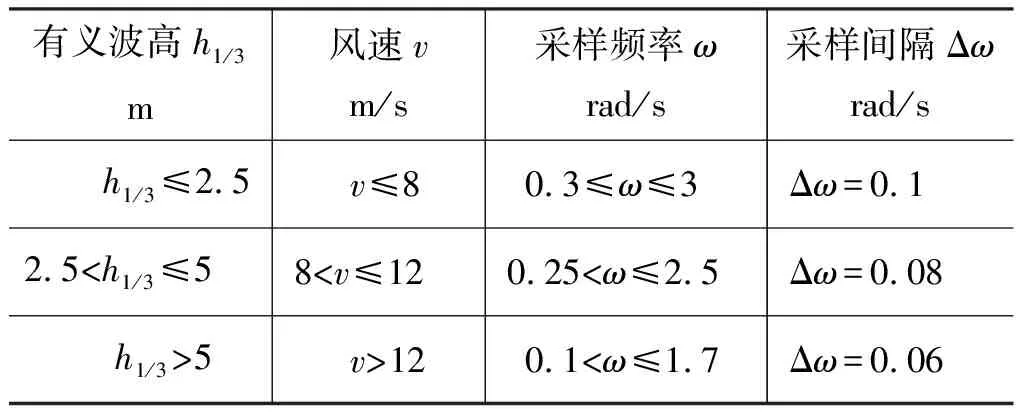
表2 海浪谱采样频段分布Tab.2 Distribution of wave spectrum sampling frequency
(10)
式中,Sy(ωi) —— 第i个遭遇波的能谱密度
ωi—— 第i个遭遇波频率
εi—— 第i个遭遇波的初相位,εi∈[0,2π]
1.3 船舶运动响应仿真
电液3-UPS/S平台在实际工况中主要功能是为了补偿船舶的横摇和纵摇方向上的运动,因此为了获得平台的运动规律,下文将对船舶在不规则海浪激励下俯仰和回转的运动响应进行求解,仿真相关参数如表3所示。

表3 仿真相关参数Tab.3 Correlation parameter of simulation
将表3中相关参数代入式(2)中,可得到6级海况条件下的海浪谱密度曲线,如图2所示。从图中可以看出,当波浪激励频率ωh∈[0.2,2.2]时,海浪谱存在有明显能量,当ωh为0.471 rad/s时,海浪能量谱达到峰值,能量峰值为2.772 m2/s。
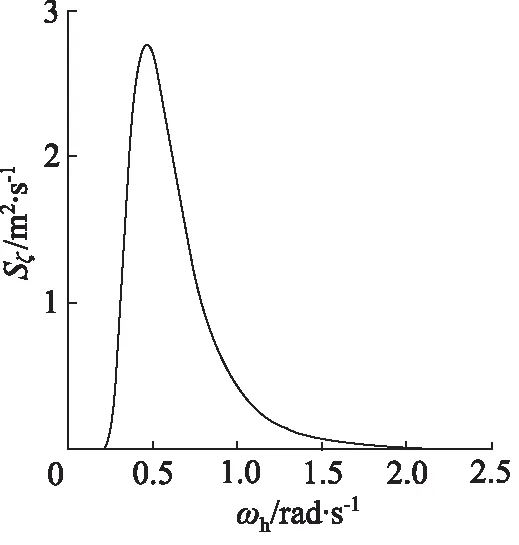
图2 海浪谱密度曲线Fig.2 Density curve of wave spectral
船舶运动的相关参数如表4所示。
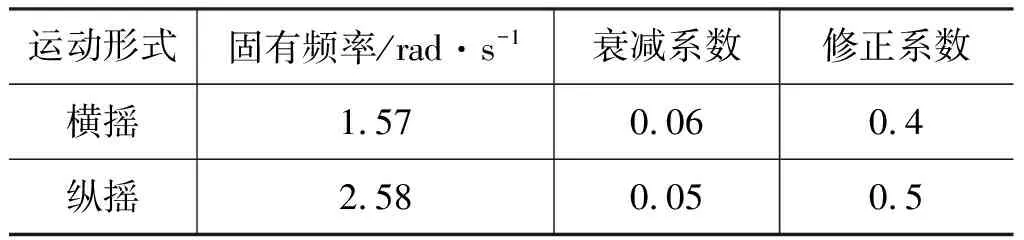
表4 船舶运动相关参数Tab.4 Related parameters of ship motion
将船舶横摇、纵摇运动相关参数代入式(8)~式(10)中即可得到船舶横摇、纵摇能量谱,如图3所示。从图3a中可以看出当波浪激励频率ωh∈[0.3,1.2]时,横摇能量谱存在有明显能量,当波浪激励频率ωh为0.696 rad/s时,船舶横摇运动能量谱达到峰值,能量峰值为0.0114 m2/s;由图3b可知,当波浪激励频率ωh∈[0.3,1.35]时,海浪谱存在有明显能量,当波浪激励频率ωh为0.933 rad/s时,船舶纵摇运动能量谱达到峰值,能量峰值为0.0254 m2/s,纵摇运动能量谱峰值约为横摇运动能量谱峰值的2倍。
仿真风速为12 m/s,根据表2可知采样间隔Δω取为0.08 rad/s,将相关参数代入式(10),可得到不规则海浪激励下的运动响应曲线如图4所示。从图4a中可看出,在船舶在6级海况下的横摇运动响应最大值约为2.625°。从图4b中可得知,船舶在6级海况下的纵摇运动响应最大值约为5.17°,对应图3的分析结果,纵摇运动响应最大值约为横摇运动响应响应最大值的2倍。横摇与纵摇运动曲线变化具有周期性,这是随机海浪运动具有周期性的结果。
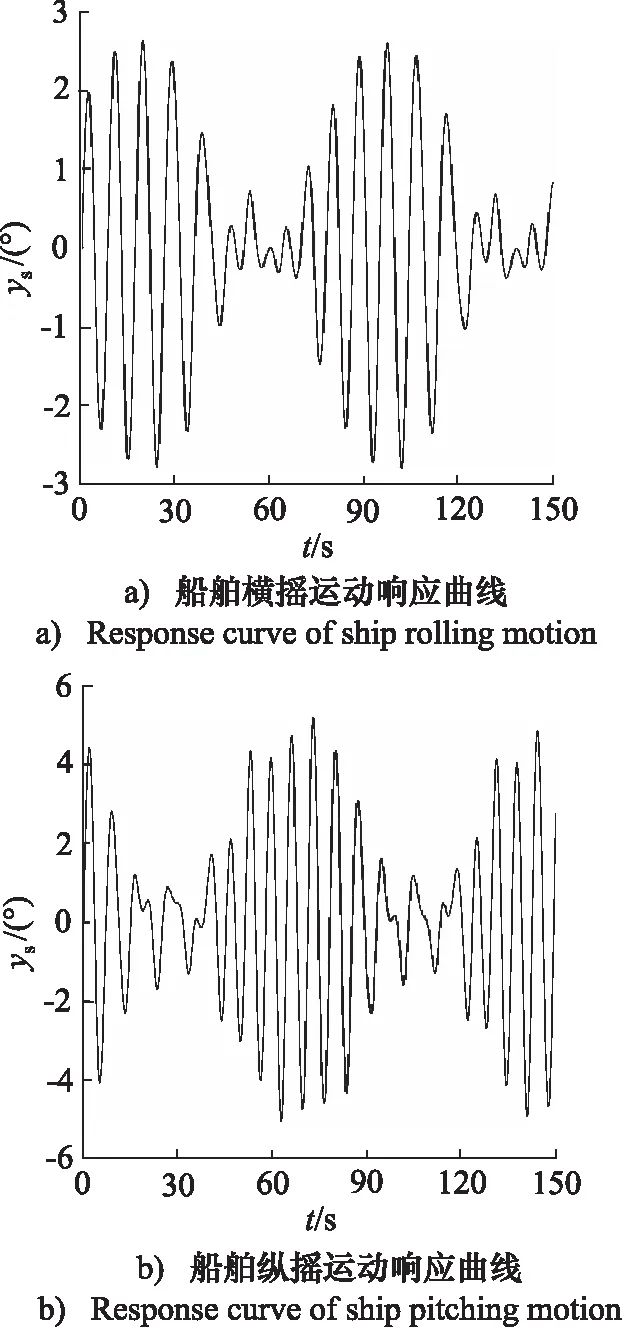
图4 船舶运动响应曲线Fig.4 Response curve of ship motion
2 电液3-UPS/S平台动力学分析
2.1 电液3-UPS/S平台姿态描述
为对电液3-UPS/S平台机构进行运动学分析,需要建立如图5所示的3-UPS/S平台系统坐标系,各坐标系意义如下。
稳定平台动平台固连坐标系U-xyz:坐标系原点U位于三角形u1u2u3的中点,x轴指向球铰中心u1,z轴垂直于动平台,y轴通过右手法则确定。
稳定平台静平台固连坐标系D-XYZ:坐标系原点D位于三角形d1d2d3的中点,X轴指向万向铰中心d1,Z轴垂直于静平台,Y轴通过右手法则确定。
船舶运动参考坐标系Os-xsyszs:坐标系原点Os固连于船舶摇荡运动的中心,xs轴指向船舶航行方向,zs轴垂直于x轴,ys轴通过右手法则确定。
船舶固连坐标系O-xyz:无扰动时坐标系方向与船舶运动参考坐标系方向平行, 当船舶由于海浪激励产生运动时方向随船舶运动方向改变。
当进行姿态补偿时,动平台固连坐标系U-xyz应时刻与船舶运动参考坐标系Os-xsyszs方向平行。动平台固连坐标系与船舶运动参考坐标系的旋转矩阵可表示为:
(11)
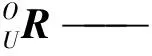
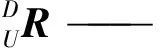
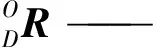
采取RPY角描述平台姿态,即选取坐标系U-xyz相对于坐标系D-XYZ3个方向的转动α,β,γ作为广义坐标,则平台的位姿也随之相应确定。依据RPY角的描述,X,Y,Z轴方向上的旋转为依次被称为回转、俯仰、偏转姿态,由此可得到坐标系U-xyz相对于坐标系D-XYZ的旋转变换矩阵为:
(12)
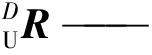
s —— sin()
c —— cos()
将船舶在随机海浪激励下的运动响应代入式(11)、式(12)中计算在6级海况下平台为保持设备的稳定的运动曲线,结果如图6所示。
对比图6a和图4a可以看出,平台回转姿态补偿角度与船舶横摇运动响应变化趋势近似相同,但是当船舶进行小幅度的横摇运动时, 回转姿态补偿角度与船舶横摇运动角度存在数值差异;对比图6b和图4b可知,平台俯仰姿态补偿角度与船舶纵摇运动响应之间存在相同的规律。由图6c可以看出,偏转方向姿态补偿角度最大值约为0.17°,且呈现一定的周期性,运动周期大于回转与俯仰姿态补偿角度的运动周期,这是船舶运动存在周期性的结果。
2.2 电液3-UPS/S平台位置分析
球铰中心ui(i=1, 2, 3)在坐标系U-xyz中的位置矢量可表示为:
(13)
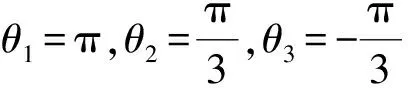
ru—— 上平台半径
万向铰中心di在坐标系D-XYZ中的位置矢量可表示为:
(14)
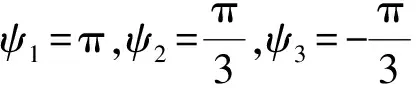
rd—— 下平台半径
建立如图7所示的支链位置矢量图,坐标系U-xyz为稳定平台动平台固连坐标系;坐标系D-XYZ为稳定平台静平台固连坐标系;局部坐标系di-xdiydizdi建立于万向铰中心处,局部坐标系ui-xuiyuizui建立于球铰中心处。zdi轴,zui轴与支链单位方向向量ei方向相同,万向铰绕着xdi轴,ydi轴的转角值分别为θdi,φdi;球铰绕着xui轴,yui轴,zui的转角值分别为θui,φui,γui;ψdi,ψui分别为万向铰和球铰的安装角度,由平台结构确定。
由图7可知,支链的闭环方程可表示为:
(15)
式中,li—— 第i条支链的长度,i=1,2,3
ei—— 第i条支链的单位方向向量
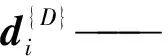
u0—— 坐标系U-xyz相对于坐标系D-XYZ的初始位移矢量
u—— 坐标系U-xyz相对于坐标系D-XYZ的位移矢量
由此可得机构的支链长度表达式为:
(16)
支链中下连杆质心位置可表示为:
(17)
式中,pgi—— 第i条支链下连杆质心位置矢量
qi—— 第i条支链下连杆质心到万向铰中心的距离
对于第i个万向铰,其局部坐标系di-xdiydizdi与坐标系D-XYZ之间的旋转变换矩阵可表示为:
(18)
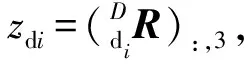
(19)
根据式(19)可计算万向铰的转角值,所得表达式为:
(20)
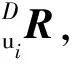
(21)
式中, (RFi)a,b为矩阵RFi的元素,i,a,b=1,2,3。
2.3 电液3-UPS/S平台速度分析
求解式(15)对时间的一阶导数,即可得到支链的速度方程为:
(22)
式中,ωzi—— 第i条支链角速度
ωu—— 动平台角速度
由此可得到支链伸缩速率与动平台角速度之间的关系为:
(23)
由式(23)可得支链与动平台之间的速度雅克比矩阵为:
(24)
计算式(22)与支链单位方向向量ei的乘积,并将结果在局部坐标系di-xdiydizdi中表示,则可得:
(25)
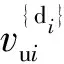
支链的角速度由万向铰的旋转产生,因此支链转动的角速度在局部坐标系di-xdiydizdi可表示为:
(26)
将式(26)中的矢量在局部坐标系di-xdiydizdi中表示,则式(26)可转化为:
(27)
结合式(25)、式(27),可得万向节转动角速度为:
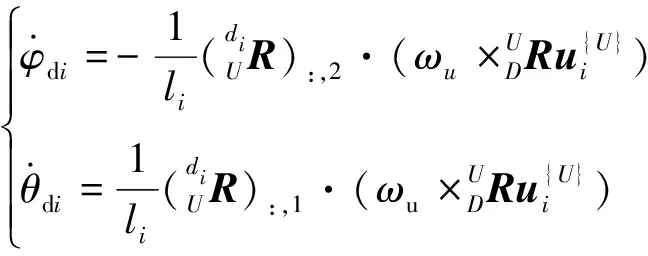
(28)
由此可以得到万向铰的速度雅克比矩阵为:
(29)
(30)
同理,考虑球铰与动平台之间的运动传递关系,支链的角速度可表达为:
(31)
将式(31)中矢量在局部坐标系ui-xuiyuizui中表示,可得到:
R(φui,yui)T(0 1 0)T+
(32)
结合式(25)和式(32)可求得球铰转动角速度表达式为:
(33)
由此可以得到球铰的速度雅克比矩阵为:
(34)
(35)
(36)
求式(17)对时间的导数,则有:
(37)
结合式(20)和式(37),可到下连杆的速度雅克比矩阵为:

(38)
同理可得上连杆的速度雅克比矩阵为:
(39)
式中,hi为第i条支链上连杆质心到万向铰中心的距离。
2.4 电液3-UPS/S平台动力学方程
为构建机构的动力学方程,需要做出如下假设:
(1) 忽略机构在加工和装配过程中所产生的误差;
(2) 支链对上平台的作用力可等效为沿着支链伸缩方向的弹簧力;
(3) 忽略各构件之间的相对摩擦。
由此计算作用在机构各构件上作用力虚功率,则由虚功率原理可得式(40):
(40)
式中,fu—— 动平台作用力矩阵
k—— 支链刚度矩阵
c—— 支链阻尼矩阵
Iu—— 动平台惯量矩阵
ωu—— 动平台角速度矢量
mgi—— 第i条支链下连杆质量
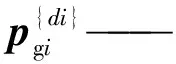
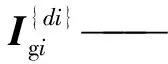
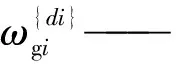
mhi—— 第i条支链上连杆质量
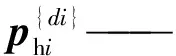
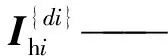
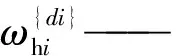
忽略科氏力和离心力,则式(40)可化简为如下形式:
(41)
由于各广义坐标相互独立,则ωu各分量也是相互独立的,则系数应全部为0,最终可得到机构的动力学方程如下:
(42)
式中,M—— 机构惯量矩阵
C—— 机构阻尼矩阵
K—— 机构刚度矩阵
(43)
(44)
(45)
3 电液3-UPS/S平台振动特性分析
3.1 电液3-UPS/S平台支链刚度分析
电液3-UPS/S平台结构参数如表5所示。
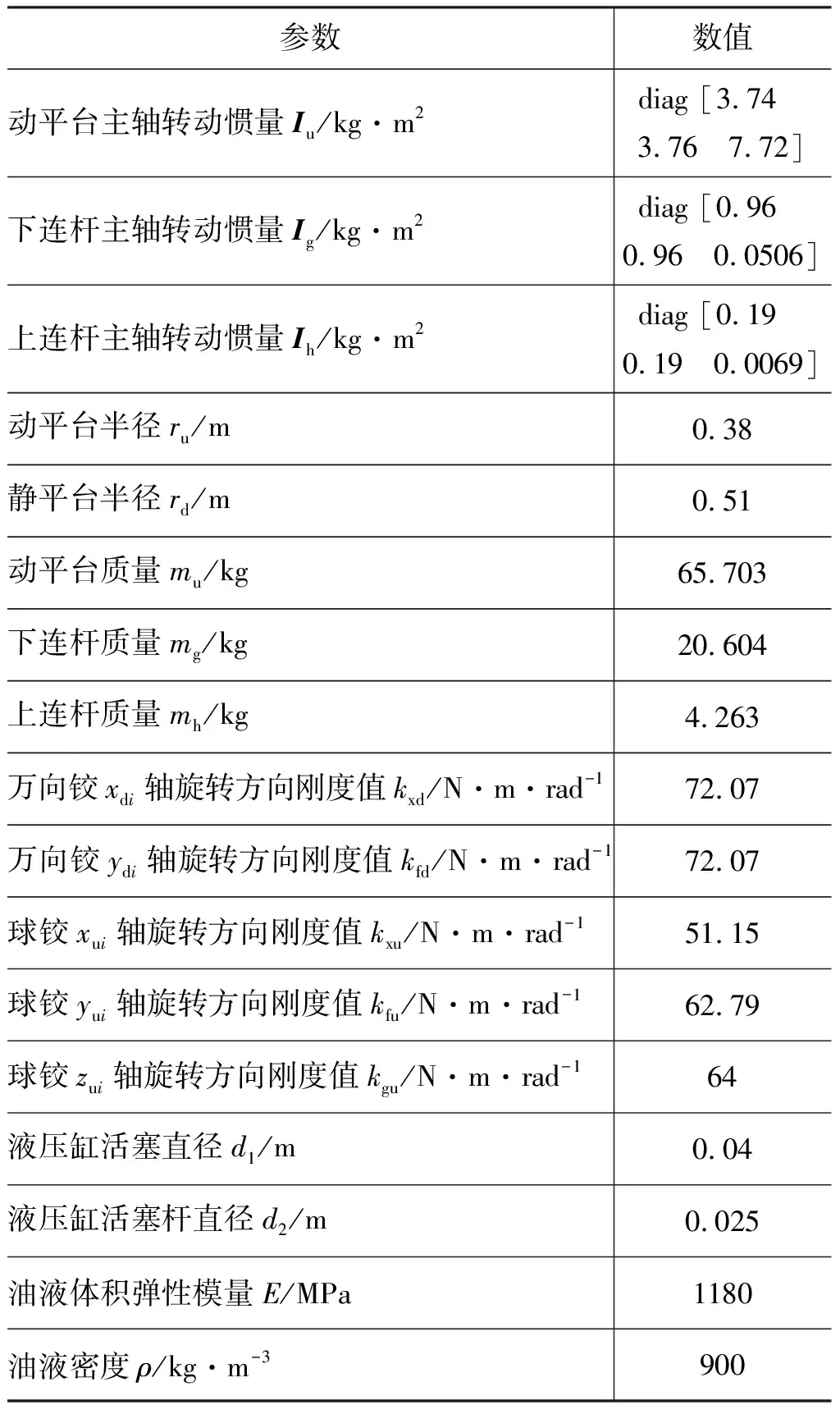
表5 电液3-UPS/S平台结构参数Tab.5 Structure parameter of electro-hydraulic 3-UPS/S platform
为避免机构的奇异位姿,取初始位姿为α=0°,β=0°,γ=28°,计算电液3-UPS/S平台机构在该位姿下的刚度矩阵,如式(46)所示:
(46)
从刚度矩阵可以看出,电液3-UPS/S平台机构在回转、俯仰方向上液压刚度数值相同,而偏转方向上液压刚度数值最小。同时可以看到在初始位姿下,刚度矩阵为轴对称矩阵,各个方向上的耦合刚度较小,基本可忽略不计,刚度矩阵可近似看作对角阵。
3.2 电液3-UPS/S平台固定位姿下模态分析
基于式(42)所示的自由振动模型和表5所示结构参数,计算了平台在初始位姿α=0°,β=0°,γ=28°和随机位姿α=10°,β=10°,γ=28°下的固有频率和模态振型,结果如表6、表7所示。
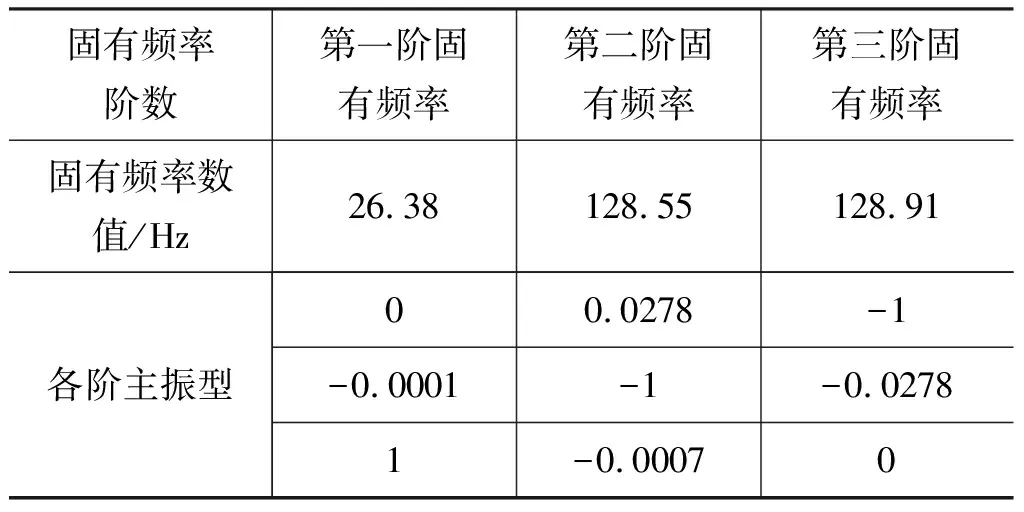
表6 初始位姿下固有频率和模态振型Tab.6 Natural frequency and mode shape at initial pose
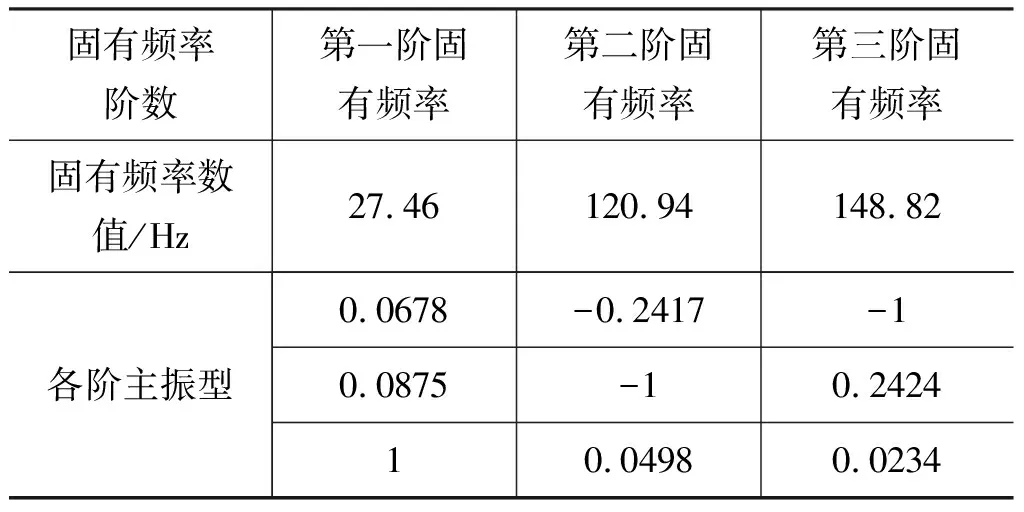
表7 随机位姿下固有频率和模态振型Tab.7 Natural frequency and mode shapes at random pose
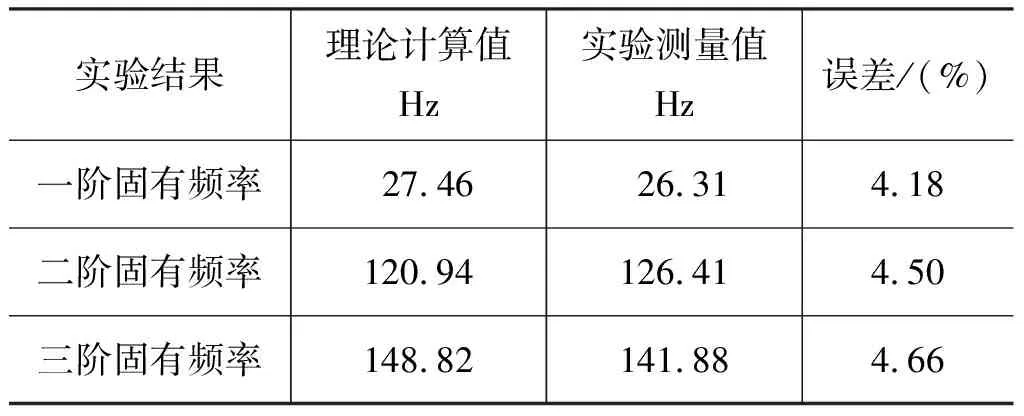
表8 模态试验结果Tab.8 Results of modal test
对表6、表7的数据分析可知,可得到如下结论:
(1) 振动频率依次为机构的各阶固有频率时,机构的最大振动响应依次出现于偏转、俯仰和回转方向,在实际工况中,激励频率最容易接近一阶固有频率,因此机构在偏转方向上最易出现共振现象;
(2) 在初始位姿下,偏转方向上固有频率最小,回转和俯仰方向上固有频率近似相等,这与刚度矩阵分析的结果一致;俯仰和回转方向上的振动响应存在一定的耦合性,但是二者与偏转方向的耦合性较小;
(3) 随着机构位姿发生改变,各方向上振动的耦合性增强,各阶固有频率数值也发生了改变,这是由于机构的速度雅克比矩阵发生改变,进而影响了机构的质量矩阵与刚度矩阵;
(4) 当机构位姿发生改变时,各阶固有频率的变化趋势并不相同,一阶、三阶固有频率增大,二阶固有频率减小。
3.3 海浪激励下电液3-UPS/S平台固有频率分析
以图6所示的平台运动曲线作为输入,通过式(42)即可得到在6级海况下电液3-UPS/S平台机构在运动过程中固有频率的变化规律,得到的最终结果如图8所示。
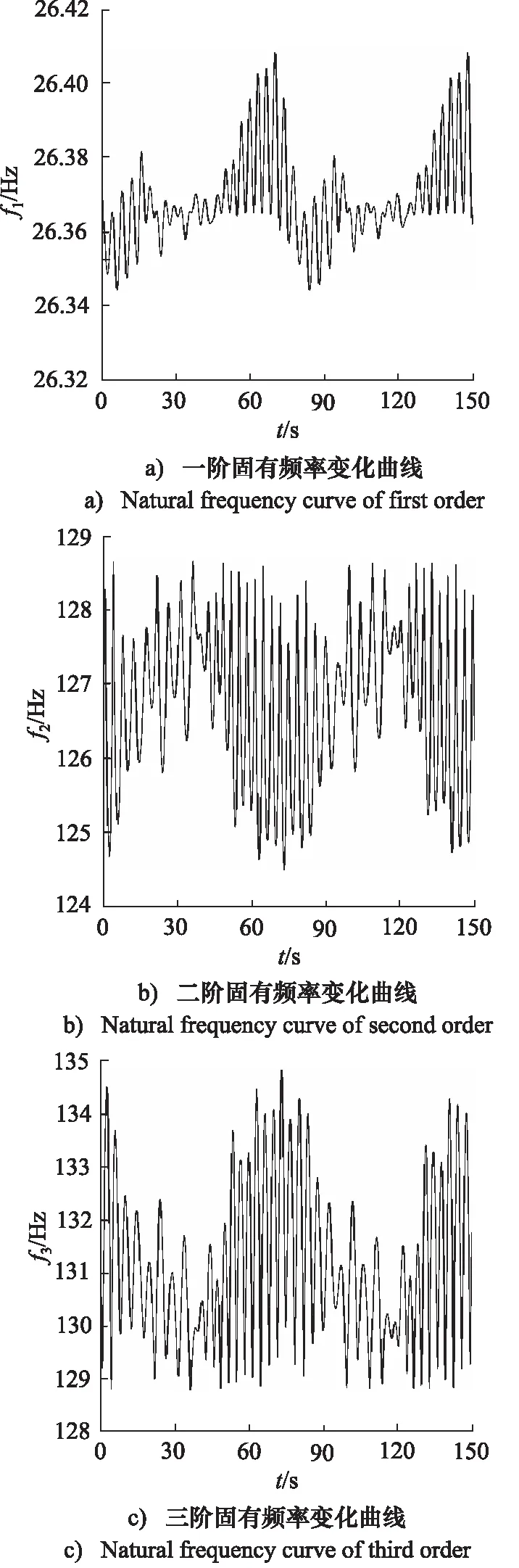
图8 固有频率变化曲线Fig.8 Natural frequency curve
从图8中可以看出,机构的固有频率随着位姿的不同而发生改变,其中一阶固有频率极差最小,对机构的位姿变化最不敏感。当机构偏离初始位姿的角度较小时,二阶固有频率和三阶固有频率近似相等,这是由于机构偏离初始位姿角度较小,机构在俯仰与回转方向上的流体等效刚度近似相等。同时,各阶固有频率变化具有周期性,这是由于机构的运动轨迹具有周期性,进而影响了机构的转动惯量与刚度。
3.4 电液3-UPS/S平台工作空间固有频率分析
由图6可知,当平台用于维持设备水平方向稳定时,偏转方向上姿态补偿角度变化范围较小,主要通过回转、俯仰方向上的运动进行角度补偿。根据工作空间搜索理论,当偏转姿态角度γ=28°时,回转、俯仰姿态角度连续变化范围最大[27],因此以该位姿作为初始工作空间,得到机构的固有频率变化曲线如图9所示。
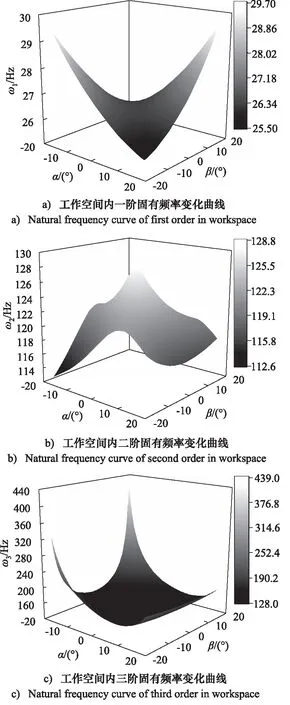
图9 工作空间内固有频率变化曲线Fig.9 Natural frequency curve in workspace
由图9可知,在偏转姿态角度不发生改变的情况下,各阶固有频率随位姿的变化呈现明显的对称性,且以一阶固有频率最为明显,对应的是偏转姿态方向上的运动。当机构逐渐偏离初始位姿时,各阶固有频率变化趋势并不相同,有的增大,有的减小。对比图9a,图9b发现,机构各阶固有频率取得最大值与最小值的姿态位置并不相同,通常情况下,当机构的俯仰姿态角度与回转姿态角度相差较大时,机构的固有频率会接近极限值,但是二阶固有频率在机构初始位姿下数值较大,当机构进行姿态补偿而逐渐偏离初始位姿时,二阶固有频率逐渐减小,并在α=-20°,β=-20°附近取得最小值。另外可以看到,一阶固有频率受姿态影响最小,二阶固有频率次之,三阶固有频率受姿态影响最大。
4 电液3-UPS/S平台动力学模型验证
为验证动力学模型的正确性,采用脉冲激振法对电液3-UPS/S平台样机进行模态试验,样机如图10所示。

图10 电液3-UPS/S平台样机Fig.10 Proto of electro-hydraulic 3-UPS/S platform
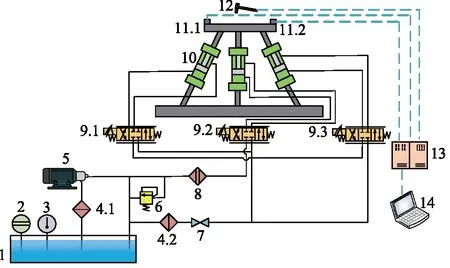
1.油箱 2.液位计 3.液温计 4.过滤器 5.电机、液压泵 6.溢流阀 7.截止阀 8.精过滤器 9.伺服阀 10.平台样机 11.加速度传感器 12.力锤 13.下位机 14.计算机图11 模态试验原理图Fig.11 Schematic diagram of modal test

图12 模态试验系统Fig.12 Modal test system
为验证自由振动理论模型的正确性,采用脉冲激振法测量3-UPS/S平台样机在随机位姿α=10°,β=10°,γ=28°下的固有频率,实验原理图如11所示。力锤敲击样机动平台给予脉冲激励,样机的加速度变化通过加速度传感器收集并传递至下位机,由此产生的力信号经由力锤自带的传感器传递至下位机,最终下位机将收集到信号传输至电脑进行储存。
实验中所用采样频率为640 Hz, 因此满足采样定理要求,采集信号具有可信度,实验所采集的激励信号与振动信号的时域曲线,如图13所示。
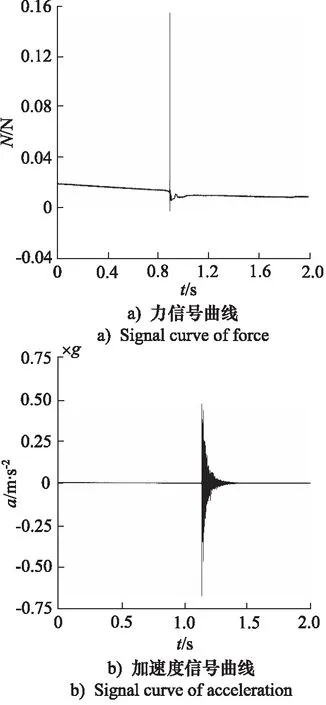
图13 测量信号时域曲线Fig.13 Time domain curve of measure signal
对图13所得数据进行数据处理,可得到样机响应信号的功率谱密度PSD曲线,如图14所示。观察图14可以看出,曲线在26.31, 126.41, 141.88 Hz处具有明显峰值,通过与机构固有频率理论值对比,理论值与实验值的最大误差为4.66%,因此可验证理论模型的正确性。
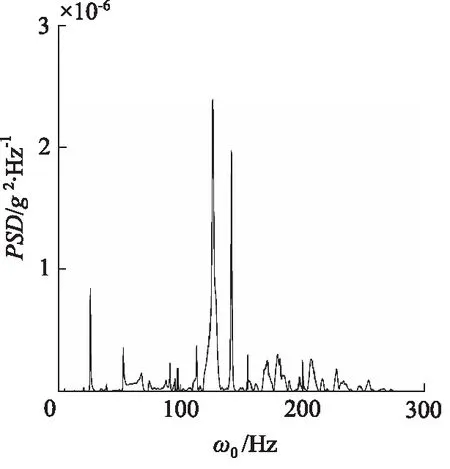
图14 功率谱密度曲线Fig.14 Density curve of power spectral
5 结论
(1) 在考虑球铰、万向铰刚度的基础上,应用虚功率原理建立了机构的动力学方程,并以6级海况下机构的姿态补偿运动曲线作为输入,分析了机构的固有频率变化规律,结果表明:当机构主要维持设备水平方向的稳定时,机构的二阶、三阶固有频率将发生显著改变,一阶固有频率则几乎不变,且固有频率的变化呈现周期性;
(2) 机构的固有频率是机构位姿的函数,在初始工作空间内,机构的固有频率变化具有对称性,取得极值的位置也并不相同,且对比发现,随着机构位姿的改变,机构的三阶固有频率变化最为剧烈,二阶固有频率次之,一阶固有频率变化最为平缓;
(3) 采用模态试验方法对理论模型进行验证,模态试验中理论频率与实际频率最大误差为4.66%,验证了振动理论模型的正确性。
