内曲线液压马达低速稳定性机理分析

2023-10-28张小龙张军辉

液压与气动 2023年10期

韩敏, 张小龙, 谭浩, 方禹, 张超, 张军辉, 徐兵

(浙江大学流体动力与机电系统国家重点实验室, 浙江杭州 310027)

引言

液压马达是将液压能转化为机械能的液压执行元件,在液压驱动系统中输出连续旋转运动[1-5]。液压马达可分为高速小扭矩和低速大扭矩两大类。径向柱塞式内曲线液压马达是一种低速大扭矩液压马达,被广泛用于绞车、挖泥船、掘进机等大型装备的回转驱动系统中[6-11]。作为执行元件的内曲线径向柱塞式液压马达可以低速直接驱动负载,但在低速工况下运转时容易出现爬行现象,进而直接影响整个装备的工作稳定性。因此,内曲线液压马达的低速稳定性是亟待研究的重要性能之一[12]。

在液压马达低速稳定性机理方面,一些学者做了相关研究。蒋文斌等[13]采用电液相似原理建立了盘配流摆线马达的数学模型,对马达动态特性及各参数对马达低速稳定性的影响进行了研究。袁兵[12]建立了考虑摩擦转矩非线性的仿真模型,并分析了轴向柱塞马达油液压缩性、转动惯量、黏滞阻尼等参数对低速稳定性的影响。林荣川等[14]通过动力学仿真和实验研究发现液压弹簧刚度和摩擦力非线性的耦合作用是液压马达低速波动的主要原因。谈宏华等[15]设计了曲轴连杆式液压马达低速稳定性机理实验系统,研究了马达压力脉动、配流盘遮盖量、外泄漏等因素对低速稳定性的影响。内曲线液压马达的结构与上述马达有较大区别,且低速稳定性问题较为突出,目前还没有针对内曲线径向柱塞马达的低速稳定性机理进行的研究分析,但上述的研究为本研究提供了有益的参考。

本研究建立了径向柱塞式内曲线马达动态特性仿真模型,从液压马达内部因素出发,对马达低速稳定性机理进行研究。对配流轴配合间隙、柱塞与缸孔配合间隙等加速导轨曲线零速区和等速区的幅角分配对马达低速稳定性的影响进行仿真分析,仿真结果进一步指导液压马达的结构设计,保障液压系统的稳定工作。

1 内曲线液压马达的工作原理

径向柱塞式内曲线马达结构如图1所示。该马达为6作用8柱塞的轴配流壳转马达,采用滚轮传力式柱塞组件结构。马达工作时,缸体1固定不动,从马达进油口进入的高压油经配流轴3进入柱塞腔,推动柱塞组件4沿缸孔做径向往复运动。柱塞组件上的滚轮作用在导轨2上,驱动导轨带动两侧壳体及与壳体相连的配流轴旋转,进而带动负载工作。在整个运动过程中,柱塞组件通过固定在缸体上的导向板5导向,仅沿缸孔轴线做往复运动,不随配流轴转动。

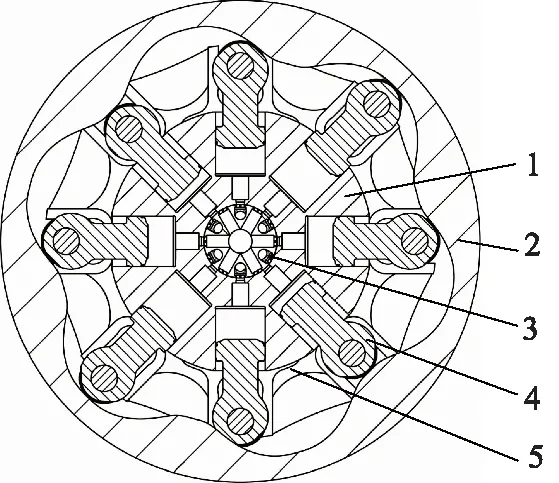
1.缸体 2.导轨 3.配流轴 4.柱塞组件 5.导向板图1 内曲线马达结构示意图Fig.1 Structure diagram of cam lobe hydraulic motor

2 低速稳定性产生机理

低速稳定性问题较为复杂。液压马达在低速下的工作特性,既取决于液压马达外部的因素,如液压系统的流量和压力脉动、负载特性等,也取决于马达本身的因素,如马达的结构参数、配合间隙值、泄漏特性及各摩擦损失特性等[16]。本研究主要从马达自身影响因素出发,分析马达低速稳定性产生机理。

当马达在低速下工作时,进入马达的理论流量较小,泄漏所占比重较大,泄漏的不稳定直接影响马达的实际工作流量,从而造成转速的波动。径向柱塞式内曲线马达的泄漏主要出现在配流轴与缸体间及柱塞与缸体间。

从马达的工作原理可以看出,马达柱塞组件的运动学特性对低速稳定性的影响较大,而柱塞组件的运动特性主要取决于导轨曲线的性质。不同的导轨曲线,柱塞组件的运动特性和力学特性也不同,因此导轨曲线的形状直接影响到柱塞运动的平稳性、转速脉动等[17-18]。尤其在低速工况下,导轨曲线对马达的输出稳定性影响较大[19]。

故针对马达两处泄漏及导轨曲线幅角分配对低速稳定性的影响进行分析。

2.1 配流轴与缸体间的泄漏

图2为马达配流轴与缸体配合示意图。缸体内部的高压油槽分别与配流轴上的油口②③相连,高压油通过配流孔进入柱塞腔推动柱塞组件运动。在回程阶段,柱塞组件将油液通过配流孔排入到配流轴内部的低压油腔中,经过油口①进入缸体的低压油槽,然后经过缸体内部流道排出。

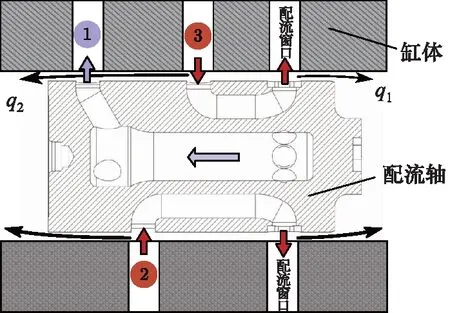
图2 配流轴配流示意图Fig.2 Schematic diagram of distribution of distributor

配流轴处的泄漏包括轴向泄漏和周向泄漏。轴向泄漏为压差流,可简化为同心圆环间隙流动[10],该压差流主要包括两部分:

(1) 缸体高压油槽②③里的高压油沿配流轴之间的环形间隙流向壳体的泄漏,泄漏量为:

(1)

式中,r—— 配流轴半径

h1—— 配流轴与缸体的间隙值

μ—— 液压油动力黏度

p1—— 高压油压力

p2—— 低压油压力

l1,l2—— 两缸体高压油槽到配流轴两端的密封线长

(2) 配流轴高压配流窗口的泄漏与缸体各配流窗口泄漏之和。在马达工作过程中,缸体固定不动,随着配流轴的旋转,两者间的配流面积及配流包角也随之变化,泄漏量也随之变化。配流轴上高压配流窗口的包角恒定,故泄漏量恒定。而单缸体柱塞腔配流包角以π/3为周期变化,在一个周期内的配流包角变化规律如式(2)所示:

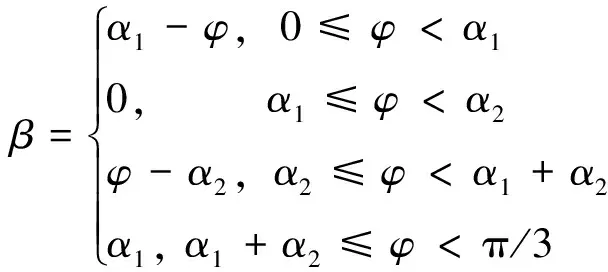
(2)

式中,α1—— 缸体配流窗口对应的包角

α2—— 配流轴配流窗口对应的包角

φ—— 配流轴转角

第i个缸体配流窗口包角为β(i),对应的柱塞腔压力为pi,故泄漏量为:

(3)

式中,l3—— 缸体及配流轴配流窗口到配流轴左侧的密封线长

配流轴的周向泄漏为剪切流和压差流,可简化为平板间隙流动[20]。其中,压差引起的泄漏主要是缸体和配流轴的高压配流窗口向两侧低压密封带的泄漏。单缸体柱塞腔与配流轴的泄漏长度l=γr以π/3为周期变化,在一个周期内的泄漏包角γ变化规律如下所示:

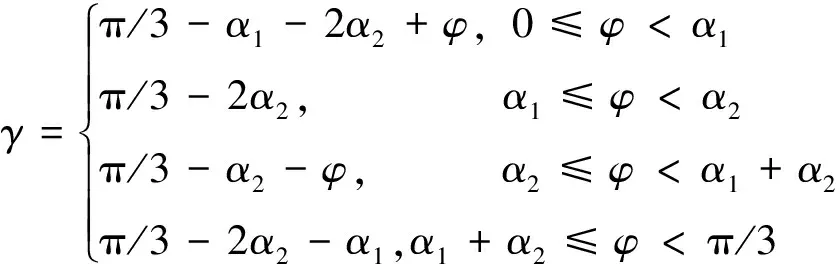
(4)

因此,配流轴周向泄漏流量公式为:

(5)

式中,b—— 泄漏宽度

v—— 配流轴旋转线速度

l(i) —— 第i个柱塞腔配流窗口与配流轴之间的泄漏长度

由以上公式可知,配流轴与缸体间轴向泄漏量Q为:

Q=q1+q2+q3

(6)

2.2 柱塞与缸体孔的泄漏

柱塞与缸体间的泄漏假设为圆柱环形缝隙泄漏,泄漏流量公式为:

(7)

式中,D—— 柱塞直径

h2—— 柱塞与缸体孔的配合间隙值

l4—— 柱塞与缸体的密封线长

2.3 等加速导轨曲线的幅角分配

如图3所示,等加速曲线是一种常用的导轨曲线,工作幅角为φx,φ0为零速区幅角,φ1为等加速区幅角,φ2为等速区幅角,φ3为等减速区幅角。幅角分配是根据设计需要,确定各区域的幅角占比,即各区域幅角与工作幅角的比值。定子导轨设计采用这种轮廓曲线,不仅能较好的解决液压马达的“困油现象”,而且通过合适的幅角分配,可使液压马达输出扭矩的脉动率在理论上达到0,进而在工作过程中产生较小的磨损和噪声。本研究探讨了该导轨曲线不同的零速区和等速区幅角占比对低速工况下稳定性的影响。

图3 等加速导轨曲线Fig.3 Constant acceleration cam ring curve

3 内曲线马达动态特性仿真模型

3.1 模型的建立

根据图1所示的内曲线马达结构及工作原理,利用仿真软件AMESim中的液压库、液压元件库、机械库、信号库等,耦合前文讨论的配流轴与缸体及柱塞与缸体间的泄漏等因素,建立单柱塞模型,如图4所示。将单柱塞模型封装为超级元件,进而建立整个马达的动态特性仿真模型,如图5所示。

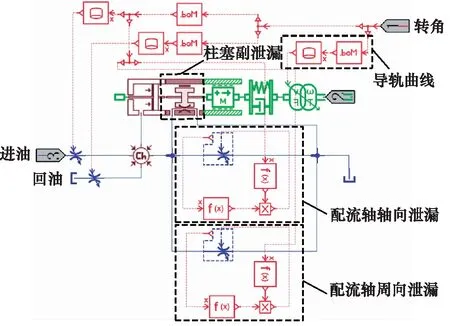
图4 单柱塞模型Fig.4 Single piston model

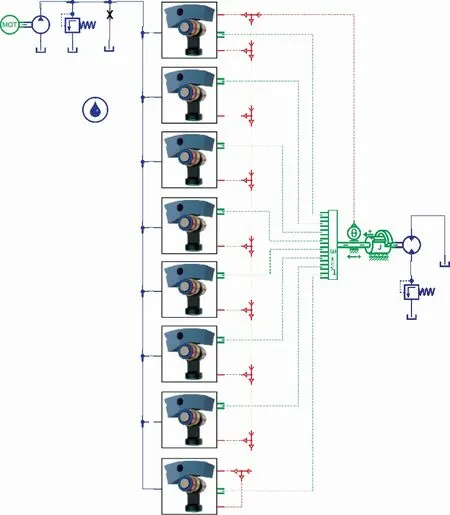
图5 内曲线马达动态特性仿真模型Fig.5 Dynamic simulation model of cam lobe hydraulic motor

3.2 参数设置

本研究建立的径向柱塞式内曲线马达动态特性仿真模型的主要参数见表1。在仿真过程中,马达的输入流量恒定。

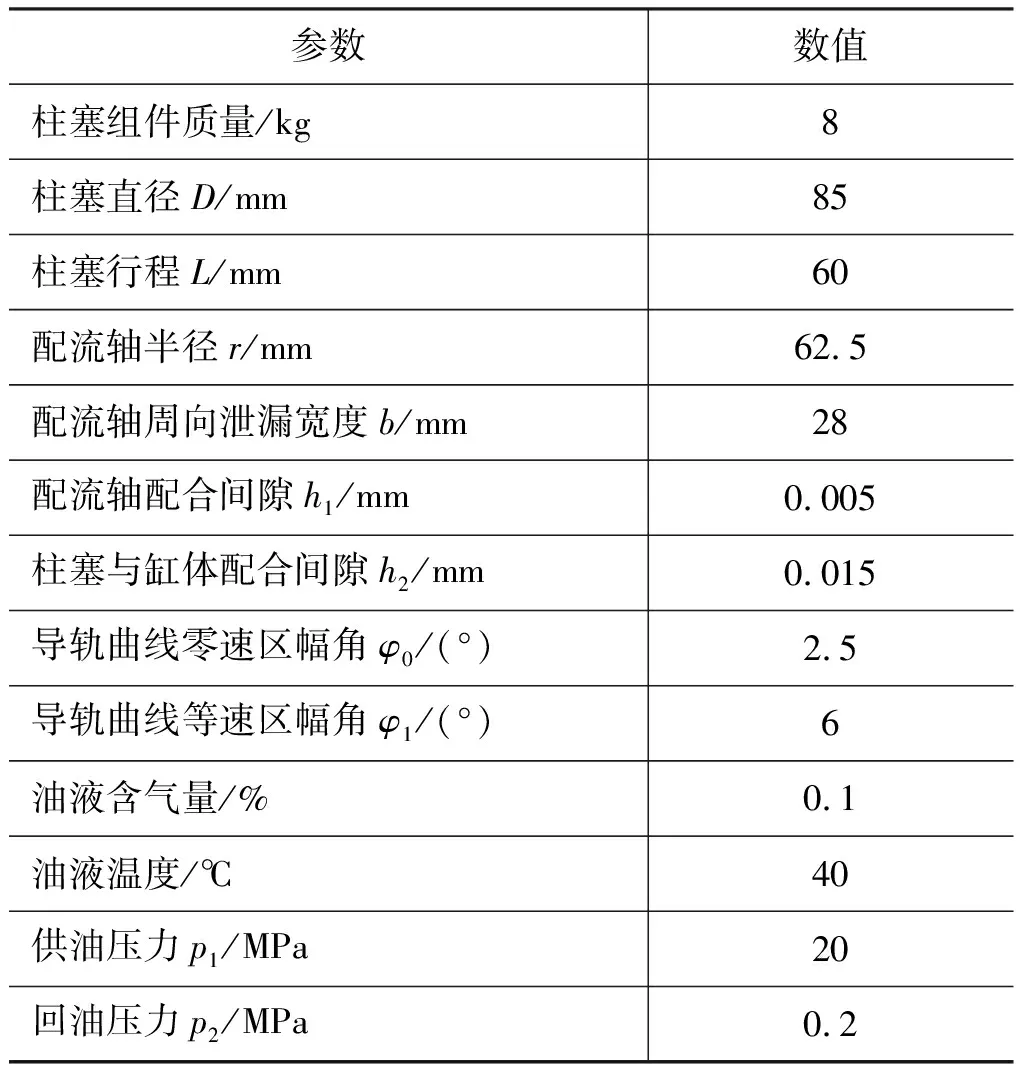
表1 马达动态特性仿真模型主要参数Tab.1 Main parameters of dynamic simulation model of motor

4 主要参数对低速稳定性影响分析

4.1 配流轴配合间隙的影响

配流轴与缸体间泄漏量的主要影响参数为配流轴配合间隙。保持其他参数不变,配流轴单边配合间隙分别设置为5,10,15,20,25 μm。不同配流轴配合间隙下,马达输出转速随时间变化曲线如图6所示,为排除马达启动特性的干扰,选取启动20 s之后的数据点进行分析,后文同上。

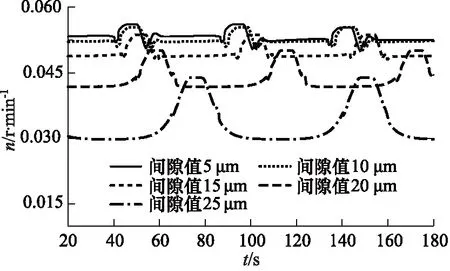
图6 配流轴配合间隙与马达输出转速的关系Fig.6 Relationship between fit clearance of distributor and output speed of motor

马达不产生爬行的临界转速称为最低稳定转速。转速脉动率K为最高与最低转速值之差与平均转速的比值。一般采用转速脉动率的10%作为是否达到最低稳定转速的判断标准[16-21]。根据图6可计算得到配流轴配合间隙与马达输出的平均转速及转速脉动率的关系,如图7所示。

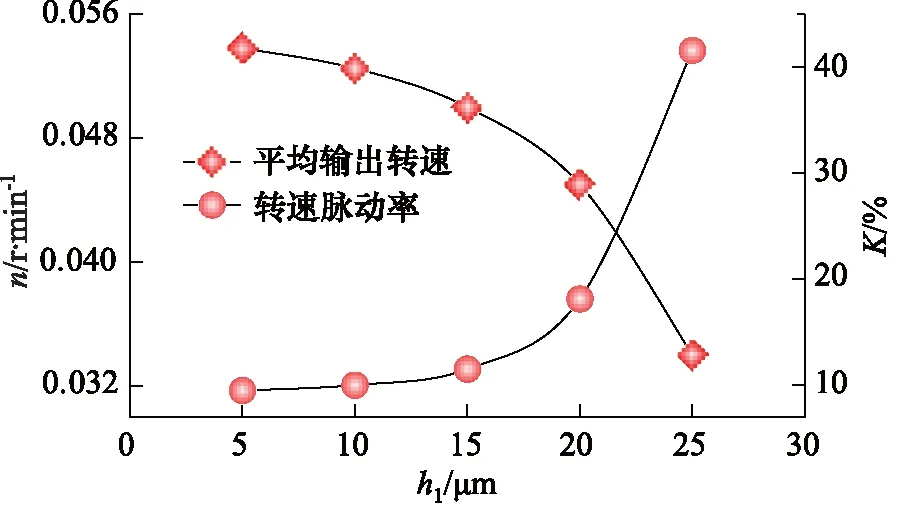
图7 配流轴配合间隙与平均输出转速和转速脉动率的关系Fig.7 Relationship between fit clearance of distributor and average output speed and rotation speed fluctuation

如图7所示,由于马达的理论流量恒定,随着配流轴配合间隙的增大,从缸体进入的高压油在配流轴处的泄漏量增大,因此进入缸体推动柱塞运动的实际流量减小,马达平均输出转速也随之减小。当配流轴配合间隙值为5 μm时,平均输出转速为0.0538 r/min,当配流轴配合间隙值增大为25 μm时,平均转速减小至0.034 r/min,下降了36.8%。由图7可观察到配流轴间隙值与平均输出转速近似呈三次方关系,因为配流轴配合间隙值与配流轴泄漏量呈三次方关系,同时,输出转速和实际流量成正比,故间隙值与输出转速近似呈三次方关系。

随着配合间隙值的增大,输出转速脉动率整体呈上升趋势,先平缓上升,后急剧上升。当配流轴配合间隙从5 μm增加到10 μm时,转速脉动率增加了0.51%,脉动率缓慢上升,转速脉动率在10%以内,马达仍能平稳运行。但当配合间隙增大到15～25 μm时,脉动率显著上升,相对于配合间隙为5 μm时,脉动率上升了2.52%,8.64%和29.52%,转速脉动率大于10%,马达处于爬行状态。因此,在设计配流轴配合间隙时,选取10 μm内的配合间隙可以实现马达在低速下的平稳运转,同时还需考虑配流轴热膨胀和加工精度等因素。

4.2 柱塞与缸体配合间隙的影响

柱塞与缸体间的泄漏量的主要影响参数为两者间的间隙值。保持其他参数不变,选取柱塞与缸孔间的间隙值为5,10,15,20,25 μm进行仿真分析。不同柱塞与缸体配合间隙下,马达输出转速随时间变化曲线如图8所示,马达输出平均转速及脉动率与配合间隙值的关系如图9所示。

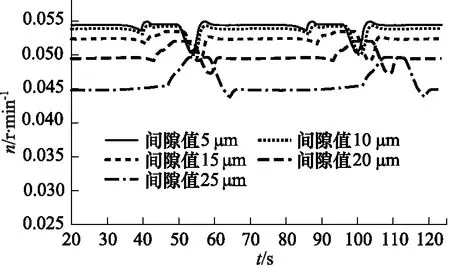
图8 柱塞与缸体配合间隙与马达输出转速的关系Fig.8 Relationship between fit clearance of piston and cylinder and output speed of motor

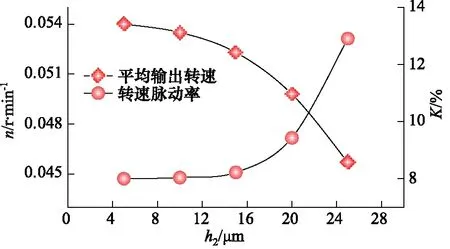
图9 柱塞与缸体配合间隙与平均输出转速和转速脉动率的关系Fig.9 Relationship between fit clearance of piston and cylinder and average output speed and rotation speed fluctuation

如图9所示,随着间隙值的增大,马达平均输出转速逐渐减小,从间隙值为5 μm时的0.054 r/min降低至0.0457 r/min。由于间隙值与泄漏量呈三次方关系,理论流量与泄漏量的差值为实际流量,实际流量与转速成正比,所以图中曲线也近似呈三次方关系。

随着柱塞与缸体的间隙值从5 μm增加到25 μm,马达转速脉动率增大了4.91%。主要原因是:随着间隙值的增大,柱塞副泄漏量增大,泄漏量随着柱塞运动及压差的变化而出现的波动增大,进而造成马达转速的脉动增加,低速稳定性变差。在以上5组仿真分析中,间隙值为5～20 μm对应的转速脉动率都小于10%,马达稳定运转,而当间隙值为25 μm时,马达处于爬行状态,稳定性较差。当间隙值在15 μm内时,马达转速脉动率变化在0.3%以内。

因此,在设计柱塞与缸体时,为了提高马达低速稳定性,应尽量减小两者间的配合间隙值,可选取20 μm内的间隙值。

4.3 等加速导轨曲线幅角分配的影响

6作用内曲线径向柱塞液压马达的工作幅角为:

(8)

1) 零速区幅角分配优化分析

零速区位于柱塞腔进油和回油的交叉点,用于防止高低压腔相通而导致内泄漏[22]。柱塞组件在零速区运动时,径向位移和速度都为0。零速区的存在会减小有效工作幅角,故选取较小的零速区幅角。保持其他参数不变,选取零速区幅角为0.5°,1°,1.5°,2°,2.5°,3.0°,3.5°进行仿真分析。不同零速区占比的幅角分配如表2所示。不同零速区幅角下,马达输出转速随时间变化曲线如图10所示,马达输出平均转速及脉动率与零速区幅角分配的关系如图11所示。

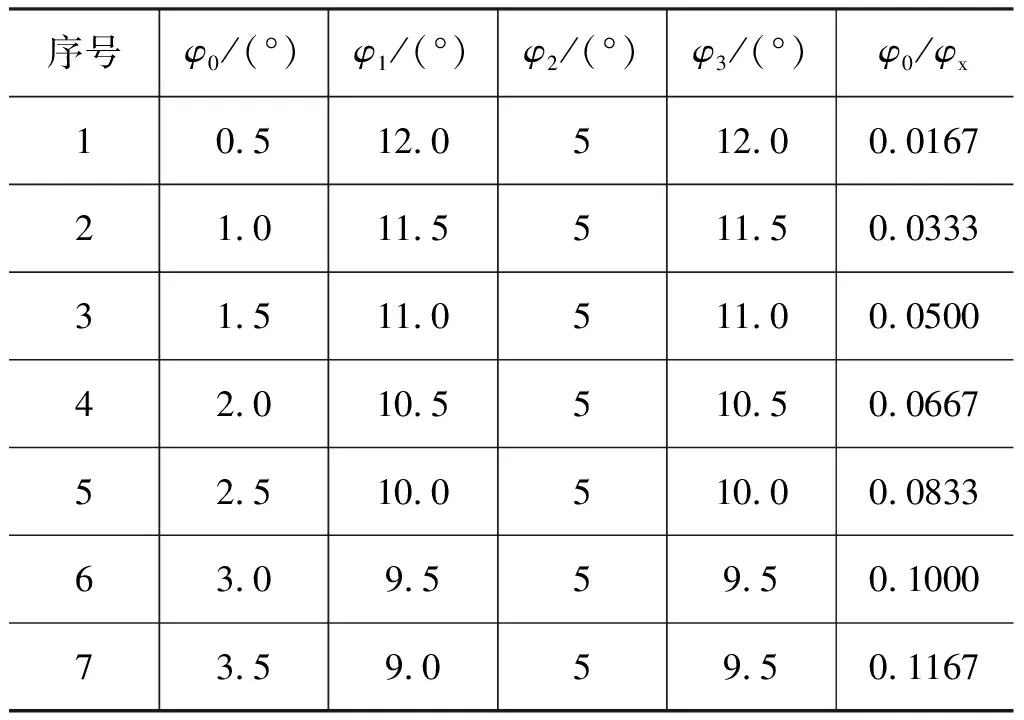
表2 不同零速区幅角分配Tab.2 Angle proportion of zero-speed region

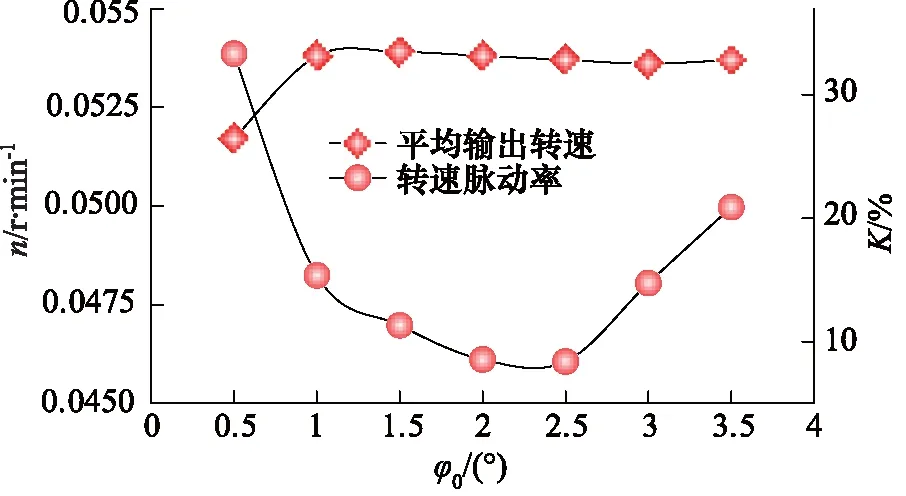
图11 零速区幅角与平均输出转速和转速脉动率的关系Fig.11 Relationship between zero-speed region and average output speed and rotation speed fluctuation

如图10和图11所示,零速区幅角在1°～3.5°范围内时,马达输出平均转速分布在0.0537 r/min附近,转速相差1%以内,而当零速区幅角为0.5°时,输出平均转速为0.0517 r/min,小于其他6组对应的输出转速值,转速相差4.26%。整体转速都分布在0.052 r/min附近,说明零速区幅角分配对马达输出平均转速值影响不大。

随着零速区幅角的增大,马达转速脉动率呈“U”形变化趋势,先减小后增大。其中,零速区幅角为2.5°对应的马达转速脉动率最小,仅为8.38%,而最大转速脉动率为33.35%, 出现在零速区幅角为0.5°时。相同流量及其他条件下, 只有零速区幅角为2°和2.5°对应的转速脉动率低于10%, 可实现在该转速下的平稳运转。而其他组的脉动率都高于10%,处于“爬行”状态。因此,零速区幅角的选择对马达在低速工况下运行的稳定性至关重要,以上7组仿真中,当零速区幅角为2.5°,即零速区占比为0.0833时,马达低速稳定性最优。

2) 等速区幅角分配优化分析

等速区用于隔离等加速和等减速区,可缓解加速度的突变并改善滚子和导轨间的接触应力。等速区的存在会减小有效工作幅角,一般分配比例小于0.3[22]。故保持其他参数不变,选取等速区幅角为0°,1.5°,3°,4.5°,6°,7.5°进行仿真分析。不同等速区幅角分配如表3所示。不同等速区幅角下,马达输出转速随时间变化曲线如图12所示,马达输出平均转速及脉动率与等速区幅角分配的关系如图13所示。

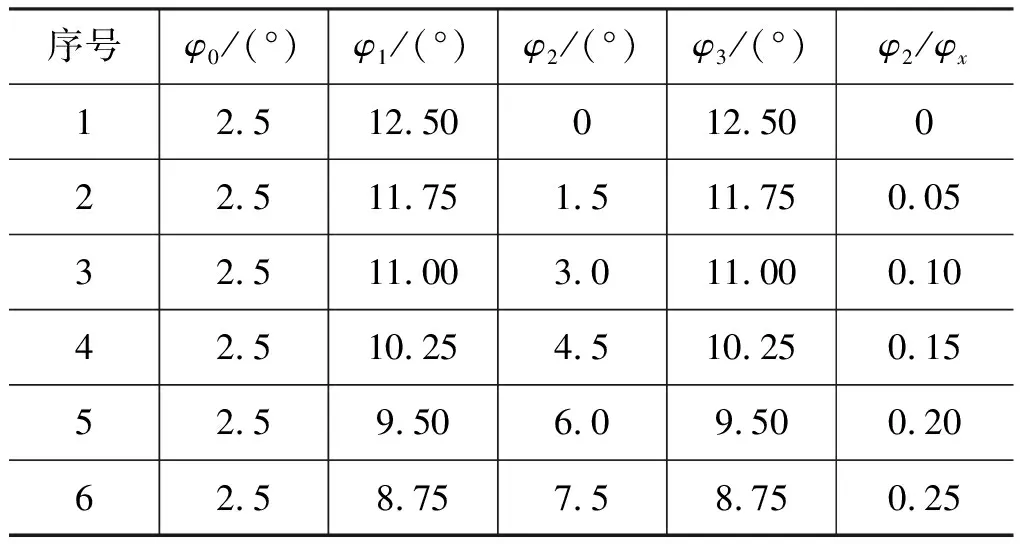
表3 不同等速区幅角分配比例Tab.3 Angle proportion of constant-speed region

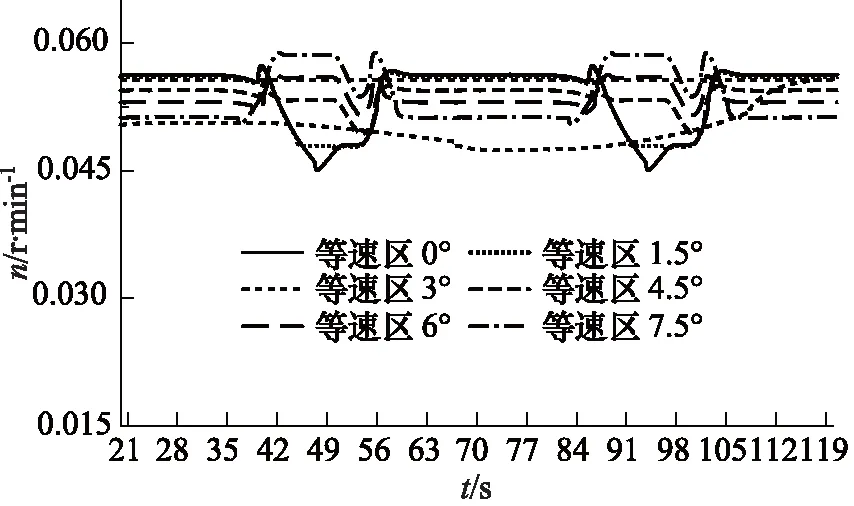
图12 等速区幅角与马达输出转速的关系Fig.12 Relationship between constant-speed region and output speed of motor

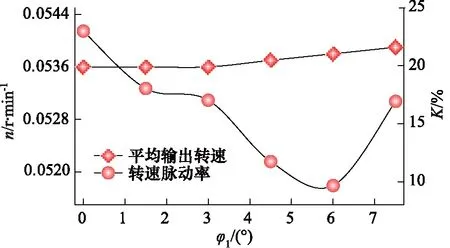
图13 等速区幅角与平均输出转速和转速脉动率的关系Fig.13 Relationship between constant-speed region and average output speed and rotation speed fluctuation

如图12和图13所示,当等速区幅角在0°～7.5°范围内时,马达平均输出转速在0.0537 r/min附近,转速相差在1%以内,说明在该范围内的等速区幅角大小对马达输出转速影响较小。

随着等速区幅角的增大,马达转速脉动率呈“U”形变化趋势,先减小后增大。最小转速脉动率出现在等速区幅角为6°时,此时的转速脉动率为9.67%。当等速区幅角为0°时,转速脉动率高达22.99%,此时等速区幅角占比为0,在等加速区和等减速区之间无缓冲区域,柱塞组件的加速度急剧变化,柱塞组件惯性力较大,柱塞运动的不平稳性进而影响输出转速的稳定性,故当等速区幅角从0°增加到1.5°时,转速脉动得到显著改善。以上六组仿真分析中,只有等速区幅角为6°时,转速脉动率低于10%,满足最低稳定转速条件,处于稳定运转状态,而其他组处于转速不稳定的爬行状态,处于转速不稳定的爬行状态。

因此,在设计导轨曲线时,需选取合适的等速区幅角使马达稳定运转,在以上6组仿真中,当等速区幅角为6°即等速区占比为0.2时,马达低速稳定性最优。