基于ICEEMDAN-ACF的自适应MEMS陀螺信号去噪方法

王 伟,冉昌艳,孙水发,祝 执,罗志会

(1.湖北省水电工程智能视觉监测重点实验室(三峡大学),湖北宜昌 443002;2.三峡大学计算机与信息学院,湖北宜昌 443002;3.三峡大学湖北省弱磁探测工程技术研究中心,湖北宜昌 443002;4.三峡大学理学院,湖北宜昌 443002)

0 引言

微机电系统(micro electro mechanical system,MEMS)陀螺因其体积小、成本低和低功耗,在工业领域广泛应用。但MEMS陀螺受制造工艺水平限制[1],其输出信号中包含大量不同类型的噪声,如何抑制噪声一直是惯导领域的研究热点之一。当前MEMS陀螺信号去噪方法主要包括低通滤波法[2]、小波软阈值法[3]、卡尔曼滤波法[4]和经验模态分解(empirical mode decomposition,EMD)去噪法[5]等。低通滤波法只适合处理平稳信号,而MEMS陀螺信号具有非平稳特性;小波软阈值法需要提前设定小波基和小波分解层数,难以进行自适应滤波;卡尔曼滤波法以建立精确的MEMS陀螺误差模型为前提,而MEMS陀螺误差的模型参数具有时变特性,通常难以建立准确的误差模型。EMD算法无需先验信息、可处理非平稳、非线性信号,被广泛应用于信号降噪领域。EMD算法[6]可将任意信号分解为多个本征模态函数(intrinsic mode function,IMF)和一个余项(Res)。MEMS陀螺信号经过EMD分解后,噪声主要分布于低阶IMF中,信号噪声含量越高,噪声主导的低阶IMF阶数越高[7],分解后的IMF可划分为噪声主导IMF、噪声有用信号混合IMF和信号主导IMF。当前基于EMD的MEMS陀螺信号去噪算法通常直接去除噪声主导IMF,之后使用小波阈值[8]、卡尔曼滤波[9]或阈值滤波[10]等手段处理噪声有用信号混合IMF,最后与信号主导IMF和余项一起重构原信号后即可完成降噪[11],有效分解噪声与有用信号和准确筛选噪声主导IMF是其中的关键。

文献[12]使用EMD算法分解陀螺信号,利用Hurst指数筛选噪声主导IMF,去除噪声主导IMF后重构信号,其在低信噪比条件下的去噪效果优于小波软阈值去噪,但其Hurst指数阈值不够精确,易丢失高频信号。文献[13]使用EMD算法分解陀螺信号,之后使用Pearson相关系数和自相关函数(autocorrelation function,ACF)方差划分IMF,剔除噪声主导IMF,利用自适应卡尔曼滤波(adaptive kalman filter,AKF)处理噪声信号混合IMF,最终降噪效果优于AKF,但Pearson相关系数筛选法仅适用于低信噪比静态MEMS陀螺信号,并且其自相关函数方差阈值为固定阈值,无法适应不同采样率的MEMS陀螺信号。上述算法均使用EMD算法分解陀螺信号,而EMD算法存在严重的模态混叠现象,有学者对EMD算法进行了改进,文献[14]提出ICEEMDNA算法,通过多次添加自适应白噪声调整信号的极值点分布,并通过多次均值运算抑制残余白噪声,较好的抑制了EMD算法的模态混叠现象。

针对上述问题,本文结合ICEEMDAN算法和小波的优点,首先使用ACF自适应阈值判断信号信噪比,使用小波软阈值对包含低能量高频成分的MEMS陀螺信号进行预降噪处理,之后使用ICEEMDAN算法分解MEMS陀螺信号,最后使用ACF自适应筛选阈值准确筛选噪声主导IMF,可以克服上述IMF筛选算法的缺陷,能够适用于不同信噪比,不同采样率的MEMS陀螺信号,抑制了高频信号丢失的现象,有效地提高了MEMS陀螺信号的去噪效果。

1 相关算法原理与分析

1.1 ICEEMDAN原理

ICEEMDAN分解步骤如下:

首先定义3个算子:Ek(·)、M(·)和<·>。Ek(·)表示EMD分解所得的第k个IMF;M(·)表示信号的局部均值:

(1)

envup(x)和envdown(x)为信号x的上包络与下包络,分别可由信号x的极大值、极小值经过3次样条插值得到;<·>表示求均值。

(2)

IMF1=x-r1

(3)

(4)

IMF2=r1-r2

(5)

(6)

IMFk=rk-1-rk

(7)

(4)k=k+1,重复步骤(3),当rk单调时停止分解,将此时的rk作为余项Res。

最终ICEEMDAN算法输出N个IMF与一个Res,x可表示为:

(8)

1.2 ACF自适应阈值与预去噪原理

1.2.1 ACF自适应阈值原理

理想高斯白噪声的自相关函数为单位冲激序列,其仅在原点有波动,方差较低,可以使用IMF自相关函数的方差作为判定IMF白噪声含量的指标:IMF自相关函数方差越低,白噪声含量越高。长度为n的序列x的自相关函数计算方式如下:

(9)

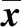
自相关函数左右对称,为降低计算量和节约存储空间,只取自相关函数右半边数据:

ACF=[R(0),R(1),…,R(n-1)]

(10)

判断噪声主导IMF的自相关函数方差阈值应当与实际高斯白噪声自相关函数方差成正比,实验表明实际高斯白噪声自相关函数方差为理想高斯白噪声自相关函数方差的1.5倍左右;同时自相关函数方差阈值应当与信号信噪比成反比,信号信噪比越低,噪声主导低阶IMF阶数越高,阈值应当更高。综上所述,自相关函数方差阈值t1可取如下形式:

(11)

式中:var(·)为方差算子;S2为信号自相关函数;S1为理想高斯白噪声自相关函数,S1=[1,01×(n-1)];var(S1)=1/n,n为信号采样点数;λ取值范围为[0.5,3],本文设置为1.5。

根据式(11)可有如下噪声主导IMF筛选方式:计算各阶IMF自相关函数方差,如果其值小于t1,则将该IMF判定为噪声主导IMF。

1.2.2 预去噪原理

ICEEMDAN算法改善了EMD算法的模态混叠现象,但在信号信噪比较低时分解信号也无法避免IMF中高斯白噪声与低能量高频信号的混叠,需要在ICEEMDAN算法分解前对包含低能量高频成分的低信噪比信号进行预去噪,降低其白噪声含量。可使用如下公式判断信号信噪比:

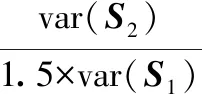
(12)

当比值低于t2时将信号判断为低信噪比信号,t2取值为1920。

预去噪使用小波软阈值处理,阈值使用Rigrsure阈值,其阈值估计较为保守,不易损失有用信号。小波分解层数过高会损失有用信号,可设置为2～4层。

1.3 ICEEMDAN-ACF自适应去噪方法

基于ICEEMDAN-ACF的自适应去噪方法流程见图1。

图1 ICEEMDAN-ACF去噪方法流程图

基于ICEEMDAN-ACF的自适应去噪方法完整步骤如下:

(1)对于包含低能量高频成分的MEMS陀螺信号,首先使用式(12)判断信号信噪比,若为低信噪比信号,则使用Rigrsure阈值进行小波预降噪,若为中、高信噪比信号,则不进行预降噪;对于不包含低能量高频成分的MEMS陀螺信号,不进行预降噪处理。

(2)使用ICEEMDAN算法分解MEMS陀螺信号,得到多个IMF与一个余项。

(3)计算各阶IMF的自相关函数方差,使用式(11)筛选噪声主导IMF。

(4)剔除噪声主导IMF后重构MEMS陀螺信号。

2 实验结果与分析

实验包括仿真信号实验与实测MEMS陀螺信号实验,对比小波软阈值法、EMD-Hurst指数法、EMD-相关系数法、EMD-ACF和ICEEMDAN-ACF 5种算法。其中EMD-Hurst指数法使用EMD分解MEMS陀螺信号,利用Hurst指数法筛选噪声主导IMF,剔除噪声主导IMF后重构原信号;EMD-相关系数法使用EMD分解MEMS陀螺信号,利用相关系数法筛选噪声主导IMF,剔除噪声主导IMF后重构原信号;EMD-ACF算法使用EMD代替ICEEMDAN,其余步骤与ICEEMDAN-ACF一致。实验中小波分解层数为3层,小波基为sym6,ICEEMDAN算法中白噪声幅度为0.3,添加白噪声的个数为150。

2.1 仿真信号实验

仿真信号使用多普勒信号,其频率和幅度随着时间改变,且包含低能量高频信号成分,进行类EMD分解后,IMF中有用信号易与白噪声产生混叠,可用来测试分解算法与去噪算法的性能。在多普勒信号中添加不同能量的高斯白噪声,对比5种算法在3 dB、15 dB和25 dB信噪比下的多普勒信号的去噪效果。去噪效果使用信噪比(signal noise ratio,SNR)衡量,计算公式如下:

(13)

式中:x(i)为不含噪信号;x′(i)为去噪后信号;N为信号长度。

15 dB多普勒信号EMD分解结果见图2,ICEEMDAN分解结果见图3。

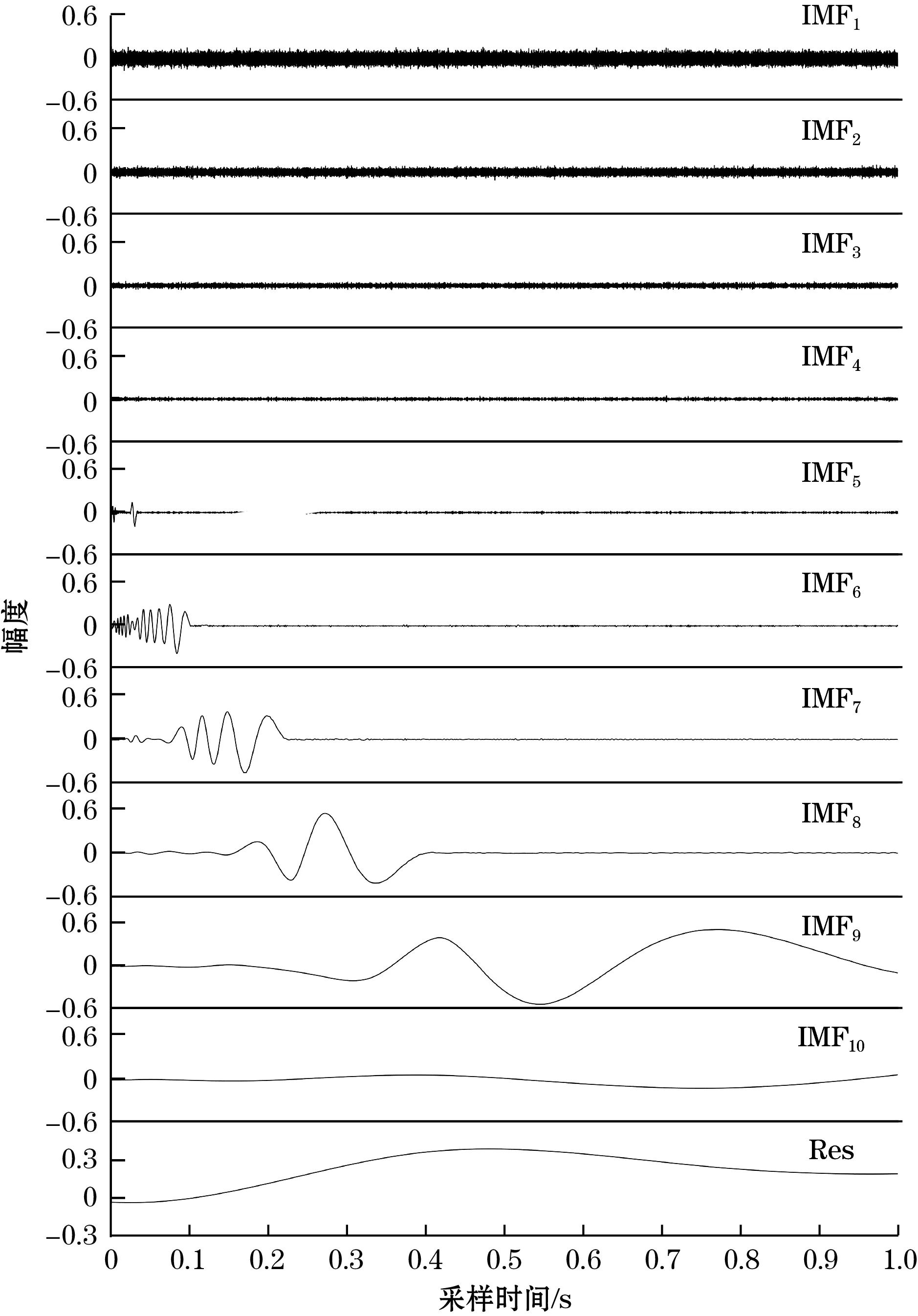
图2 15 dB多普勒信号EMD分解结果

(a)IMF1～IMF9

图2中,EMD分解的IMF5和IMF6中混叠了部分高斯白噪声,并且IMF5中的部分信号与IMF6产生了混叠;图3中,ICEEMDAN分解的IMF9和IMF10中混叠了部分高斯白噪声,但白噪声含量低于EMD算法分解所得的IMF5和IMF6,且其信号主导IMF之间未产生混叠。

15 dB多普勒信号进行EMD分解后各阶IMF的Hurst指数见图4、各阶IMF与原信号的Pearson相关系数见图5、各阶IMF的自相关函数方差见图6;进行ICEEMDAN分解后各阶IMF的自相关函数方差见图7。

图4 Hurst指数(EMD)

图6 自相关函数方差(EMD)

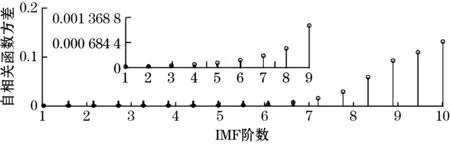
图7 自相关函数方差(ICEEMDAN)

图2中,1～4阶IMF为噪声主导IMF,5～10阶IMF为信号主导IMF。文献[12]将Hurst指数位于[0.25,0.75]之间的IMF判定为噪声主导IMF,图4中5～7阶信号主导IMF被误判定为噪声主导IMF;文献[13]将与原信号的Pearson相关系数位于[0.2,1]之间的IMF判定为噪声主导IMF,图5中7～9阶信号主导IMF被误判定为噪声主导IMF;15 dB多普勒信号的ACF自适应阈值t1为6.844×10-2,图6中EMD-ACF将第5阶IMF误判定为噪声主导IMF,IMF5中部分有用信号混叠于IMF6中,导致其有用信号成分较低,且IMF5中残留噪声较多,导致其被筛选为噪声主导IMF。上述3种方案均有部分信号主导IMF被错筛选为噪声主导IMF而被剔除。

图3中1～8阶IMF为噪声主导IMF。图7中,ICEEMDAN-ACF将1～8阶IMF判定为噪声主导IMF,IMF9和IMF10并未相互混叠,并且其白噪声含量相对较低,不会影响噪声主导IMF的筛选,实现了噪声主导和信号主导IMF的准确筛选。

15 dB多普勒信号去噪前后波形对比见图8。图8中,小波软阈值法残留噪声较多;EMD-Hurst指数法丢失了信号高频成分;EMD-相关系数法只保留了噪声;EMD-ACF同样丢失了部分信号高频成分;ICEEMDAN-ACF未损失有用信号成分,残留噪声最少,去噪效果最佳。

3 dB多普勒信号去噪前后波形对比见图9。图9中,小波软阈值法有较多噪声残留;EMD-Hurst指数法、EMD-相关系数法和EMD-ACF均会不同程度丢失有用信号高频成分;ICEEMDAN-ACF去噪效果最佳。

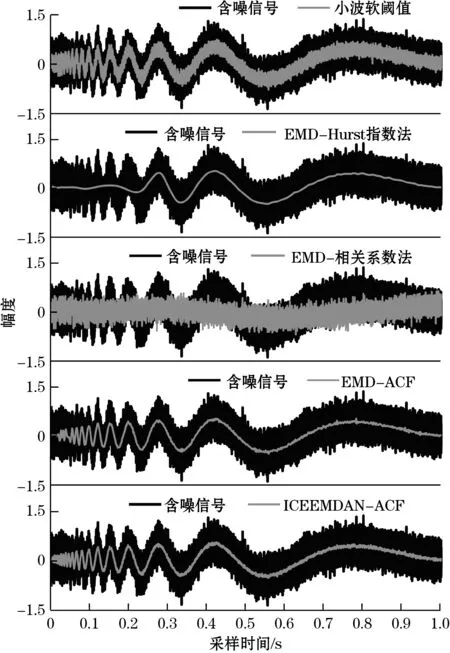
图9 3 dB多普勒信号去噪结果

3 dB多普勒信号包含大量高斯白噪声,根据式(12)计算其阈值小于t2,需要使用小波软阈值进行预降噪处理,图10给出了不预降噪处理和采用预降噪处理的ICEEMDAN-ACF算法去噪后的3 dB多普勒信号高频部分波形对比。

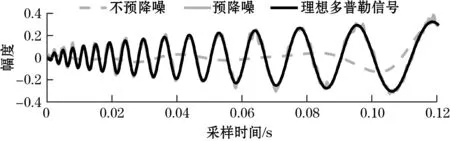
图10 3 dB多普勒信号预降噪高频部分波形对比

图10中,使用小波软阈值对3 dB多普勒信号进行预降噪后,ICEEMDAN-ACF算法在高频部分的去噪效果得到极大改善,有效抑制了高频信号成分丢失的现象。

25 dB多普勒信号去噪前后波形对比见图11。图11中,小波软阈值法仍然有较多残留白噪声;EMD-ACF未丢失高频信号成分,但其残留白噪声含量高于ICEEMDAN-ACF;EMD-Hurst指数法和EMD-相关系数法仍然丢失了信号高频成分;ICEEMDAN-ACF未损失有用信号成分,残留噪声最低,其去噪效果最佳。

图11 25 dB多普勒信号去噪结果

3种信噪比的多普勒信号去噪前后的信噪比对比见表1。

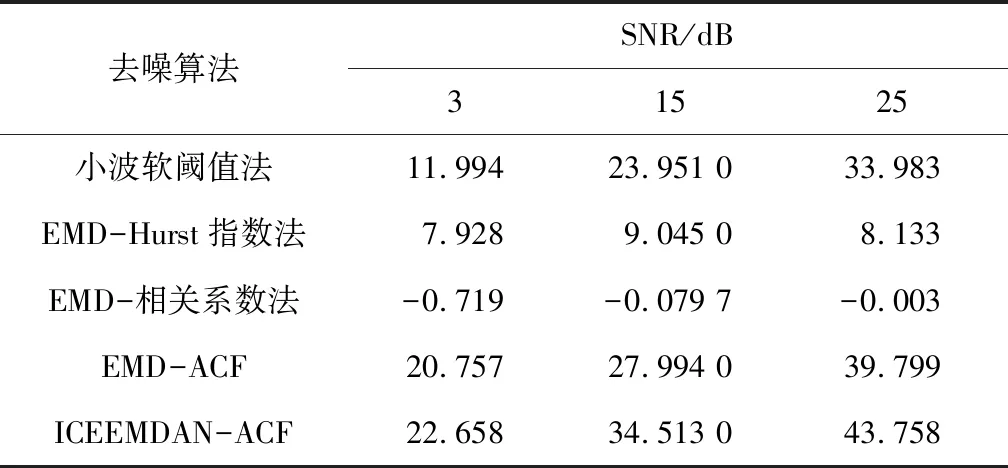
表1 多普勒信号去噪前后的信噪比比较

表1中,ICEEMDAN-ACF在低、中、高3种信噪条件下去噪后的信噪比均高于小波软阈值法、EMD-Hurst指数法、EMD-相关系数法和EMD-ACF。

2.2 实测MEMS陀螺信号实验

实验使用MTi-100-2A8G4惯性测量单元(inertial measurement unit,IMU),采集14 min静态陀螺数据,采样频率为200 Hz。静置IMU时,陀螺测量地球自转角速度,其频率低于0.2 Hz[15],不包含低能量高频成分,不必进行小波软阈值预去噪。实验使用x轴陀螺数据,x轴陀螺信号去噪前后波形对比见图12。

图12 实测MEMS陀螺信号去噪结果对比

图12中,小波软阈值法和EMD-相关系数法滤波后仍存在较多残留白噪声,EMD-Hurst指数法、EMD-ACF和ICEEMDAN-ACF滤波后基本不存在白噪声残留。

实验使用去噪后的信号方差评估MEMS陀螺信号去噪的效果[16],结果对比见表2。

表2 实测MEMS陀螺信号去噪前后方差对比 10-8deg·s-1

表2中ICEEMDAN-ACF滤波后信号方差最低,其去噪效果最佳。

3 结束语

针对白噪声统计特性,提出一种可适应不同采样率、不同信噪比MEMS陀螺信号的ACF自适应阈值来筛选噪声主导IMF,并结合小波软阈值预去噪,抑制了低信噪比情况下信号高频成分丢失的现象,最终仿真实验和实测MEMS陀螺信号实验表明所提自适应ACF筛选方法筛选效果优于相关系数筛选法和Hurst指数筛选法,所提ICEEMDAN-ACF方法可有效抑制MEMS陀螺信号的随机噪声。