基于组态王软件的流量—液位前馈反馈控制方法研究与实现

刘勇，周振华，厉昂，谷雪冬，张金祥

国电电力大连庄河发电有限责任公司，辽宁大连 116431

0 引言

计算机技术突飞猛进的发展，带动了标准的工业计算软件技术的变革，在此背景下，新的工业控制系统正以硬件平台构成的集成取代传统的封闭式系统。占据工业控制领域主导地位的上位机（PC 机）具有广阔的市场前景，同时带动了组态软件的发展。在实际操作的控制系统中，Windows 系统下的组态软件，如组态王（KINGVIEW）为控制系统提供了强大的人机界面和通信功能。本文设计了一个基于组态王的水箱液位前馈反馈控制系统，既发挥了前馈作用及时克服主要扰动对被控量影响的优点，又保持了反馈控制能克服多个扰动影响的特点，从而实现水箱液位的前馈反馈控制。系统实时监控水箱液位数值，确保系统运行的稳定性，同时提高控制的准确性。

1 基于组态王的流量—液位前馈反馈控制方法实现

1.1 水箱液位前馈反馈控制的硬件系统

水箱液位定值控制的前馈反馈控制器由组态王组成。组态王负责数据采集、输出控制量和对整个控制过程的监控。水箱液位前馈反馈控制的硬件系统主要包括A3000 过程控制系统、百特表、压力传感器、电动调节阀和计算机[1-2]。A3000 现场系统是一种基于现场总线的过程控制系统，通过连接液位传感器、压力传感器等外部设备的I/O 模块，实时采集各种过程参数的数据，如图1 所示。

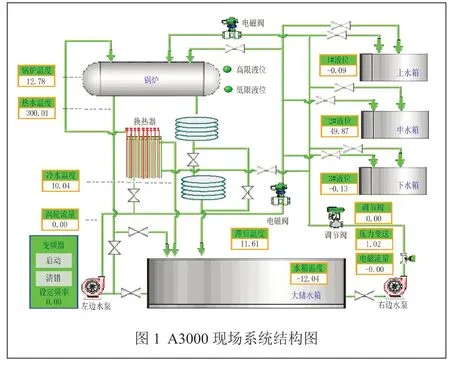
A3000 过程控制系统实现了多个控制系统的连接和协同工作，同时通过网关系统与不同类型的设备进行连接，以实现全面的控制和监控，系统结构如图2所示。

1.2 水箱液位前馈反馈控制的软件系统

水箱液位前馈反馈控制的软件系统采用的是北京某公司生产的组态王和MATLAB。

1.3 水箱液位前馈反馈控制的设计方案

基于组态王的单容水箱液位前馈反馈控制系统里，组态王负责接收从采样设备传来的液位采样值，同时把控制量传递给调节阀，并负责对整个控制过程的监控。建模对系统进行仿真的过程采用数学应用软件MATLAB 来得以实现[3]。控制逻辑如图3 所示。

在本设计中，定值需要保持水箱液位，主要扰动量是流量，对其进行前馈控制，被控变量是水箱液位，对其进行反馈控制。

综上所述，用组态王软件实现系统的控制功能，通过设计流量—液位的前馈反馈控制方法，实现实验室的过程控制同步实验。

2 组态界面的开发

2.1 建立组态王新工程

在组态王软件中建立新工程，选择一个工作目录，用于存储工程所需的各种文件和数据，包括图形界面设计文件、数据采集配置文件、控制逻辑脚本文件等。通过工作目录来进行文件管理可以使系统更加有序和高效。

2.2 定义IO 设备

在组态王软件中，IO 设备通常包括下位机（PLC、仪表、模块、板卡、变频器等）和通过网络连接的其他计算机。通过与组态王软件进行连接和交互，下位机可以接收来自软件的控制指令，并向软件反馈设备状态、测量数据等信息。为方便定义和配置外部设备，组态王软件提供了“设备配置向导”，通过该向导，用户可以一步步完成设备的连接和配置。

2.3 定义变量

在组态界面的开发过程中，定义变量是非常重要的一步。通过定义变量，可以在组态界面中实现对数据的传递和管理。定义变量是组态界面开发中的基础步骤，通过合理定义和使用变量，可以实现界面的功能和交互效果。图4 为变量“fmtov1”的信息总结列表。

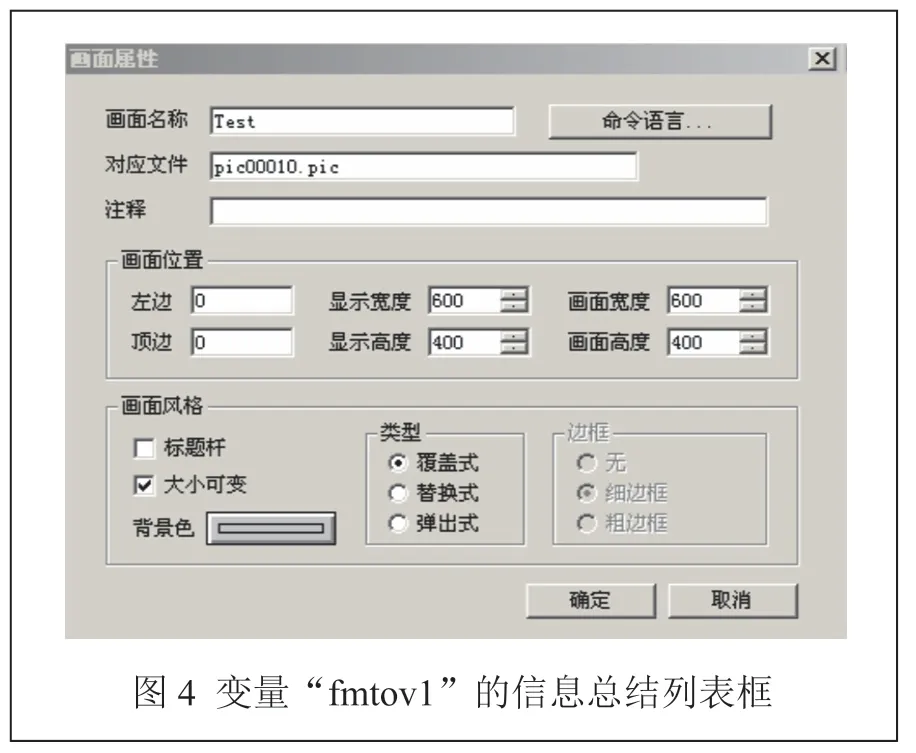
2.4 组态画面的创建

在组态王软件的操控界面浏览器左侧选择大纲项中的“文件画面”双击“新建”图标，弹出新建的操作界面，在开发系统中利用工具箱进行组态画面的设置，选择相应的属性后，确定结果显示出组态画面，如图5 所示。

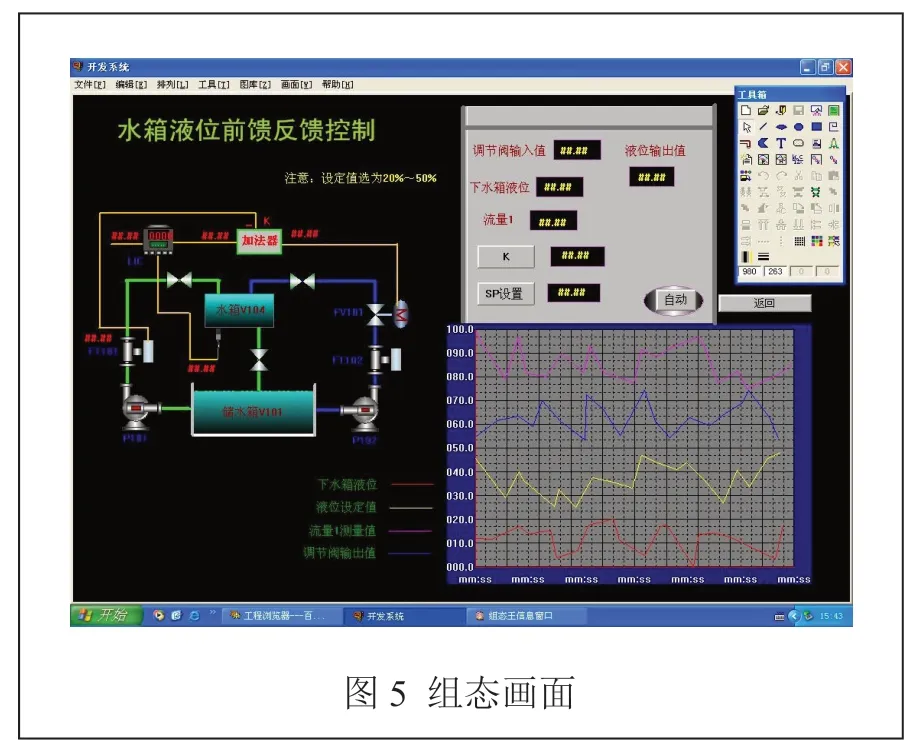
2.5 建立动画连接

建立变量 ＂fmtov＂ 的动画连接并设计模拟数值，模拟数值确定后，界面出现输出对话框，如图6 所示。在实际运行时，确保动画连接与实际变量的数值同步更新，确保显示的数据准确反映变量的状态。

点击操作界面菜单上的编辑命令，点击属性，选择命令语言，此时操作者在窗口编辑画面中编辑命令语言，进行上位机和下位机之间数据传递。在本文的设计中，为了将采样液位最终传递到MATLAB，同时将MATLAB 计算出的控制量最终传递到电动调节阀，需要输入的命令语言为：fvtom =测量值a；过程值b=fmtov；其编辑窗口如图7 所示。

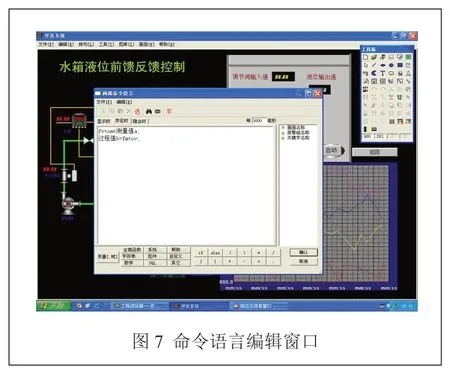
通过以上4 个步骤，组态王就可以利用定义的变量与百特表交换数据，同时利用设计的组态画面对整个过程进行监控。

3 水箱液位前馈反馈的控制算法及MATLAB 仿真

3.1 前馈反馈控制原理

在负载干扰量变化的测量中，采用前馈控制策略实时抵消干扰并保持被调量稳定。在实时控制中，前馈控制的主要目的是通过提前获得和处理干扰信号来提高控制系统的抗干扰能力。通过计算出的校正值来确定按照某种物质或能量平衡所需的条件。在稳态时，通过测量系统的扰动干扰，计算出校正值来补偿这些干扰。通过前馈控制和校正值的应用，有效地抵消负载干扰，维持被调量的稳定性，并满足系统所需的条件。

前馈—反馈控制系统原理图如图8 所示，用两个水泵注水，设法保持下水箱液位。

系统经过计算测量得出干扰数值，一旦支路发生干扰动作，系统不通过调节器直接进行补偿，动作指令传达另一支路，通过对调节阀开度做以调整与其相互匹配。

系统在执行命令动作过程中，如果遇到开环控制，系统存在余差并且无反馈，增加反馈通道，使用PI 进行控制。

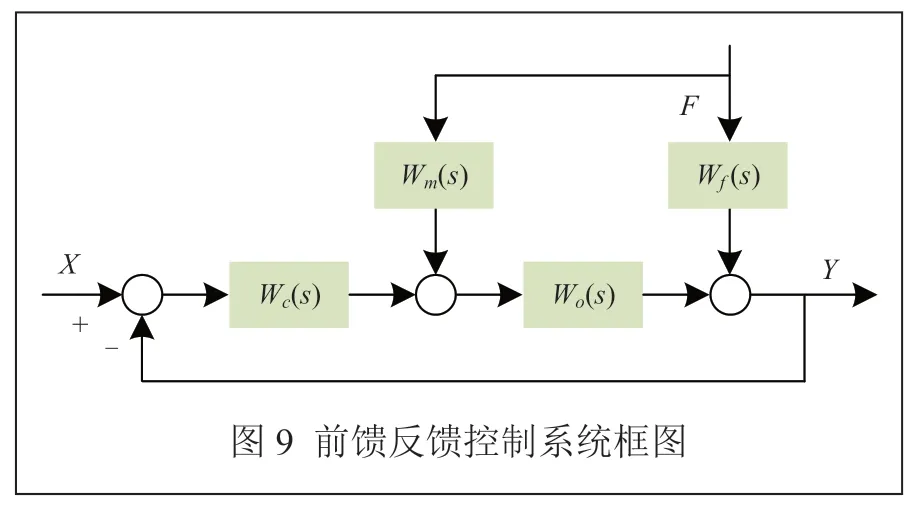
图9 为前馈反馈控制系统图，此系统为复合系统，由反馈回路和开环补偿回路相互叠加产生。在扰动F(s)作用下，系统输出为：

其中，Y(s)表示系统的输出信号，是系统对输入和扰动的响应结果；F(s)表示扰动的输入信号，是系统受到的外部干扰或变化；Wf(s)表示开环补偿回路的传递函数，用于对输入信号F(s)进行补偿，以抵消扰动的影响；Wm(s)表示开环补偿回路和反馈回路之间的传递函数，用于调节开环补偿和反馈之间的相互作用；Wo(s)表示反馈回路的传递函数，将系统的输出Y(s)反馈到系统输入中，以实现对系统性能的控制和优化；Wc(s)表示反馈回路和系统输出之间的传递函数，用于调节反馈和系统输出之间的相互作用。

在公式（1）中，开环补偿回路的传递函数Wf(s)和Wm(s)抵消扰动的作用，通过对F(s)进行补偿和调节，以最小化干扰对系统输出的影响；而反馈回路的传递函数Wo(s)和Wc(s)则负责对系统的输出进行校正和调节，以确保系统输出Y(s)稳定且符合要求。通过公式中各个变量的相互作用和调节，该复合系统能够同时利用开环补偿和反馈控制来抵消扰动，优化系统性能，并实现对系统输出的稳定和控制。

扰动量F(s)对被控量Y(s)的影响：Wm(s)Wo(s)F(s)是前馈控制作用；Wc(s)Wo(s)Y(s)是反馈控制作用。

在给定X(s)作用下，系统输出为：

在扰动和给定作用下，系统输出为：

3.2 前馈反馈控制器的设计及MATLAB 仿真

3.2.1 前馈补偿

加前馈是为了消除扰动对系统影响，即：

所以，

3.2.2 反馈补偿

PID 控制器的输出值v(t)取决于系统给定值r(t)和系统输出值y(t)的偏差e(t)、偏差的积分、偏差的微分的线性加权组合，即：

其中，TI表示积分时间常数；TD表示微分时间常数；KP表示比例系数；表示积分系数；KD=KPTD表示微分系数；变量dt定义了时间间隔或采样周期，用于离散化PID 控制，通常，dt表示两次控制信号计算之间的时间差。

位置式PID 控制算法：

其中，偏差e(k)是指系统给定值和输出值的差异，k表示离散时间步长，位置式PID 控制算法根据偏差的累积误差（积分项）和最近两个采样时刻的偏差变化率（微分项）；KP表示比例增益，用于调整根据偏差计算的控制输出的幅度；KI表示积分增益，用于调整根据偏差累积误差计算的控制输出的幅度；KD表示微分增益，用于调整根据偏差变化率计算的控制输出的幅度。

在该算法中，偏差e(k)通过比例增益进行反馈，误差的累积和通过积分增益进行反馈，偏差变化率通过微分增益进行反馈。这样的组合可以综合利用偏差、偏差累积误差和偏差变化率，从而更好地调节控制输出。

增量式PID 控制算法：

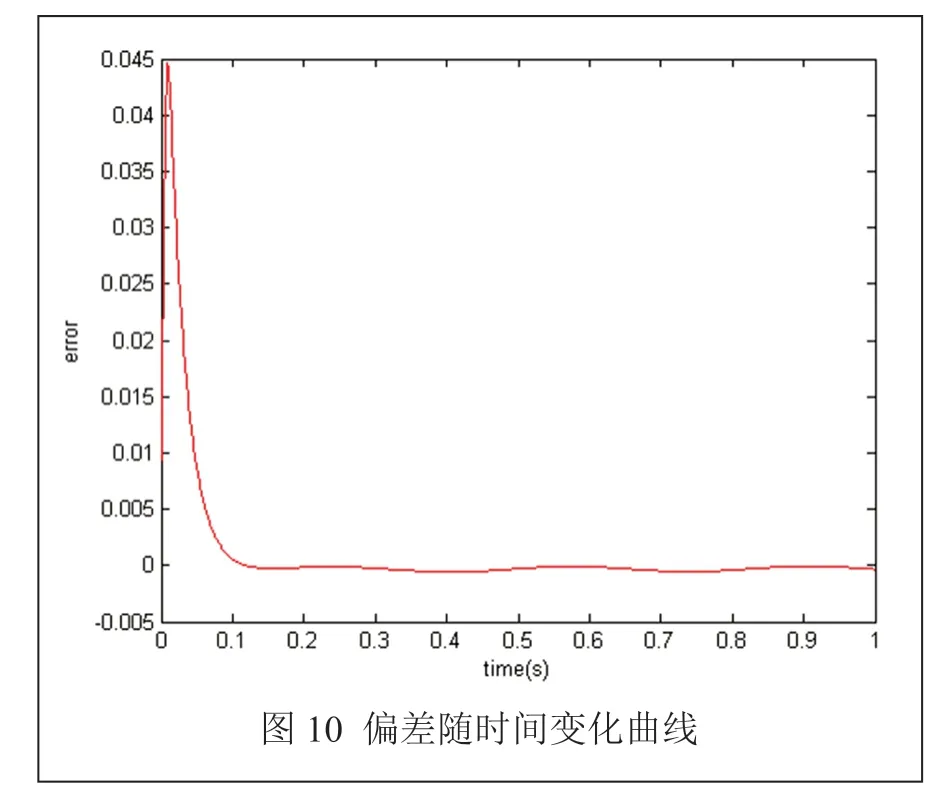
反馈补偿是指通过对系统的输出值与给定值之间的偏差进行测量和调节，以实现对系统的控制和优化。在PID 控制器中，反馈补偿是通过比例、积分和微分的线性加权组合来实现的。在位置式PID 控制算法中，PID 控制器的输出值v(t)取决于偏差e(t)、偏差的积分和偏差的微分的线性加权组合。比例系数KP控制着偏差的比例部分，积分系数TI控制着偏差的积分部分，微分系数KD=KPTD控制着偏差的微分部分，用于计算PID 控制器的输出，以调节系统的控制量，使其接近给定值。在增量式PID 控制算法中，PID 控制器的输出值Δu(k)通过当前控制量u(k)与上一时刻的控制量u(k-1)之间的差值表示。这种算法主要用于离散时间的控制系统，在每个采样周期中根据当前偏差和历史控制量的变化来更新控制器的输出。以上为前馈反馈补偿的实现基础，编辑程序，运行后得到仿真图10 ～12。

图10 为系统偏差，即给定液位与实际液位的差值，可以看到，液位很快达到给定值。

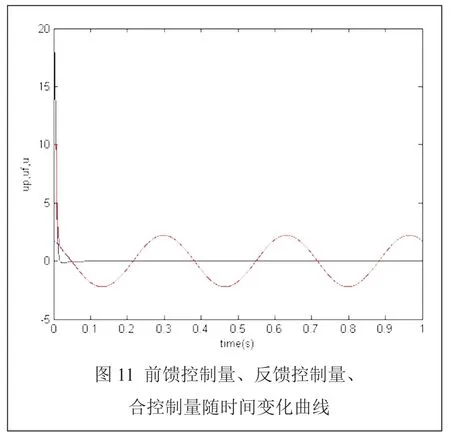
前馈控制量是基于前馈补偿而得出的对调节器的控制量，由于仿真输入的给定量为正弦信号，所以补偿作用也随之变化，图11 中蓝线为前馈控制量。

反馈补偿起作用是由于系统在初始设定的给定值与系统输出存有偏差，对调节器的控制量进行反馈补偿，若系统无偏差，说明给定值与系统输出数值一致，没有反馈控制量。图11 中黑线为无反馈控制量，数值为0。

合控制量即前馈反馈补偿对调节器的最终作用量。开始时，由于给定值与系统输出有偏差，加上在前馈作用下，导致合控制量比较大，当无反馈控制量时，系统合控制量即为前馈控制量，故与前馈控制量重合，图11 中红线为合控制量。

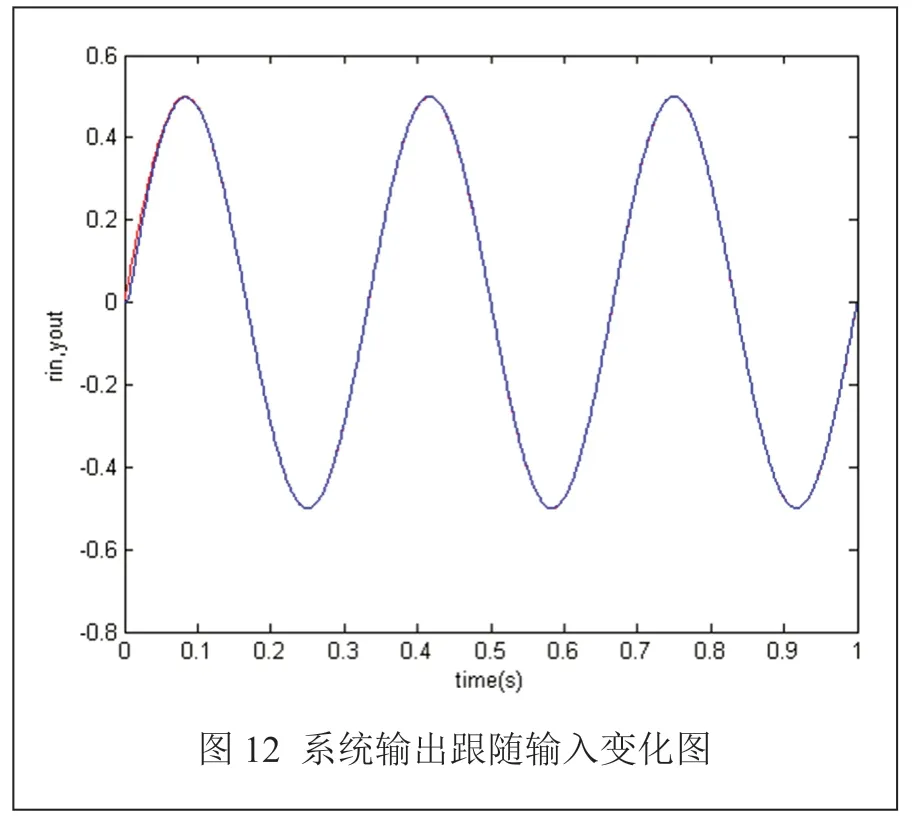
仿真时，参考输入量为正弦信号，主要观察输出跟随输入情况，由图12 可知，开始时，输出与输入存在偏差，通过调节，输出值与输入值相等，曲线重合，即输出可以有效跟踪输入。

4 水箱液位前馈反馈控制的整体调试

为了使系统设计达到最佳效果，需要输入不同测试数值进行实验比对，以便更好地显示出水箱控制液位[4-5]。

4.1 调试过程

调试过程的一般步骤如下：

（1）在A3000-FS 上，打开手动调节阀JV104、JV103、1#电磁阀、JV201、JV206，其余阀门关闭；

（2）在A3000-CS 上，电磁流量计输出的流量与AI2 进行匹配，涡轮流量计输出的流量与AI0 进行匹配；下水箱液位连接到A11；AO0 连接到电动调节阀（FV101）；

（3）打开A3000 电源，在A3000-FS 上，启动左边水泵和右边水泵，左边水泵使用变频器控制；

（4）启动计算机组态软件，点击进入工程式，进行水箱液位的前馈反馈控制；

（5）进入组态王的运行环境；

（6）控制液位由启动调节器来设置，在组态王监控操作界面中，通过显示屏的水位视图，多次输入参数变化进行调节，最终达到最佳控制效果。

4.2 调试结果

将实际控制效果与预期的控制效果进行比较。调试过程中注意逐步调整参数，观察每次调整的效果，同时掌握合适的参数范围，以避免不稳定或不可控的控制结果[6-7]。最佳控制参数程序如下：

%PID Feedforward Controler

clear all;

close all;

ts=0.001;

sys=tf(133,[1,25,0]);

dsys=c2d(sys,ts,'z');

[num,den]=tfdata(dsys,'v');

u_1=0;u_2=0;

y_1=0;y_2=0;

error_1=0;ei=0;

for k=1:1:1000

time(k)=k*ts;

A=0.5;F=3.0;

rin(k)=A*sin(F*2*pi*k*ts);

drin(k)=A*F*2*pi*cos(F*2*pi*k*ts);

ddrin(k)=-A*F*2*pi*F*2*pi*sin(F*2*pi*k*ts);

%Linear model

yout(k)=-den(2)*y_1-den(3)*y_2+num(2)*u_1+num(3)*u_2;

error(k)=rin(k)-yout(k);

ei=ei+error(k)*ts;

up(k)=80*error(k)+20*ei+2.0*(error(k)-error_1)/ts;

uf(k)=25/133*drin(k)+1/133*ddrin(k);

M=2;

if M==1%Only using PID

u(k)=up(k);

elseif M==2%PID+Feedforward

u(k)=up(k)+uf(k);

end

if u(k)>=10

u(k)=10;

end

if u(k)<=-10

u(k)=-10;

end

u_2=u_1;u_1=u(k);

y_2=y_1;y_1=yout(k);

error_1=error(k);

end

figure(1);

plot(time,rin,'r',time,yout,'b');

xlabel('time(s)');ylabel('rin,yout');

figure(2);

plot(time,error,'r');

xlabel('time(s)');ylabel('error');

figure(3);

plot(time,up,'k',time,uf,'b',time,u,'r');

xlabel('time(s)');ylabel('up,uf,u');

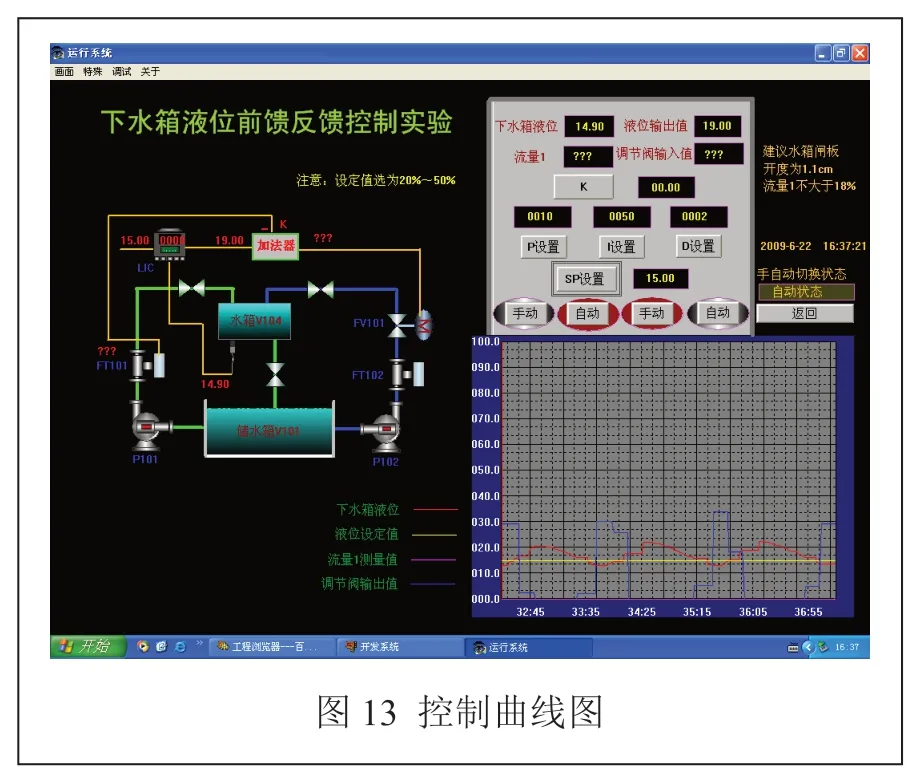
图13 是15 cm 时的控制效果图。可以看出，系统控制效果良好，基本能够满足系统设计所要求的各项指标。

5 结束语

水箱液位前馈反馈控制器是基于组态王实现的，充分发挥组态王可视化、易操作的优点，达到比较好的控制效果。组态王中开发组态界面包含IO 设备的定义、数据库的建立、监控画面的设计以及动画连接的实现。本文采用MATLAB 编辑前馈反馈控制算法进行仿真，经反复对比实验得出前馈反馈控制算法的最佳参数。其控制曲线结果表明，系统具有很好的控制效果，达到预期指标。整套水箱液位前馈反馈控制原理简单，编程容易。采用前馈反馈控制，使系统能在扰动出现时就进行控制，从而更有效地消除扰动对被控参数的影响，提高生产效率，减少大量的人力、物力，有利于降低生产成本。在控制复杂的工业过程时，尤其是在需要同时控制多个变量时，利用MATLAB 与组态王的组合使用，进行复杂的数学计算，方便实现对各个变量的控制，将其应用到实际的工业生产过程，具有较好的社会效益和商业价值。