碳滑板表面波纹对高速列车受电弓气动特性影响

安 睿 ,任尊松 ,陈厚嫦 ,魏 雪 ,吴养民

(1.北京交通大学 机械与电子控制工程学院,北京100044,2.中国铁道科学研究院集团有限公司,北京 100081)

高速列车在轨道行驶过程中通过受电弓获取电能来保障列车的稳定运行。随着列车速度不断提高,列车系统受到的空气阻力对列车的制约作用显著增加。列车空气阻力主要来自于头车、尾车、车体连接处、转向架以及受电弓等部位,目前大多数列车减阻降噪方式都是基于上述除受电弓以外的结构开展研究,并且对于列车头部、裙板及风挡的优化设计逐渐趋于成熟。实际上,良好的受电弓气动特性对列车速度的提升起着至关重要的作用,因此可以通过优化受电弓结构来提高整体列车系统的空气动力性能。

目前国内外针对受电弓的气动噪声及气动力的研究较多,吴燕等[1]采用数值分析方法模拟仿真了高速受电弓的空气动力学性能并且得出受电弓主要有3个噪声源:弓头、上框架及下框架。下框架噪声辐射可以通过加装导流罩减小高速气流的作用来改善,此时弓头的噪声影响范围远大于上框架,改善受电弓气动性能的优化措施应着重于弓头部位。刘海涛等[2]基于仿生结构设计了6种受电弓杆件模型,通过仿真分析得出椭圆形截面杆件相比于圆形截面有更低的气动阻力及气动噪声,基于椭圆形截面仿生环状波纹杆件结构能够获得最优的减阻降噪效果。李田[3]比较了受电弓不同运行状态下的气动力,得出在同一速度等级下受电弓开口运行下的气动阻力及气动升力要比闭口运行时的气动力大2%～8%,且当运行速度不小于400 km/h时,受电弓气动阻力受空气压缩效应的影响较大,气动升力受空气压缩效应的影响较小。杨康[4]分析了受电弓的空气动力特性,表明针对整个受电弓的气动力而言,弓头的气动阻力和气动升力占比较大,弓头的气动抬升力对整个弓网的受流质量影响明显,因此优化受电弓弓头结构可以有效改善受电弓整体的气动特性。针对单独的受电弓弓头杆件,LIU 等[5]在方形杆件迎风侧与背风侧都引入了展向波纹结构,利用数值仿真分析得出增加展向波纹结构可以使得杆件阻力系数与气动噪声显著减小,该结果通过试验得到了验证,展向波纹结构可以使得基本涡流脱落得到有效抑制。BEARMAN 等[6]对迎风面与背风面包含展向波纹结构的受电弓杆件进行了风洞测量分析,展向波纹度对常见钝体绕流影响的试验研究结果与不含展向波纹杆件相比,阻力降低了至少30%。此外,当波峰与波峰高度之比除以波长超过0.06和0.09时,涡流脱落被完全抑制。张长亮等[7]针对受电弓弓头方形杆件引入了展向波纹结构,通过对8种参数不同的包含展向波纹结构的弓头滑板进行了数值仿真对比分析,最终得出了降噪性能最优及减阻性能最优时对应的滑板展向波纹结构参数。LEE 等[8]对受电弓弓头进行了流线型优化,并通过与带有矩形弓头的受电弓气动特性进行对比验证了优化的有效性,利用风洞试验测量了受电弓的气动力,根据受电弓的组成进行了气动力分析。

研究表明,受电弓的气动性能对列车速度的提升以及运行安全性具有显著影响,其中弓头的气动性能是主要影响因素,而通过对受电弓弓头结构优化来减小受电弓气动阻力的研究相对较少,未有通过设置弓头波纹对整车进行分析来改善受电弓气动性能的研究。鉴于受电弓以闭口运行时列车的气动特性优于开口运行,受电弓安装在远离列车运行方向的位置时气动噪声相对较低[9],因此本文采用数值模拟方法分析了安装在远离列车运行方向车顶处的受电弓在闭口运行时弓头波纹位置对受电弓气动特性的影响,研究成果可为改善高速列车受电弓的气动特性及结构设计提供参考。

1 受电弓流场分析理论

1.1 受电弓流场湍流控制方程

受电弓周围的复杂绕流场的流体流动所遵循的三大物理守恒定律为:质量守恒定律、动量守恒定律以及能量守恒定律。上述定律表述成数学形式,就是如下所示的控制方程[10]:

(1) 质量守恒方程。单位时间里,微元体内流体质量的增加量和同时间内流入该微元体的净流体质量相同。质量守恒定律对应的连续性方程又称为质量守恒方程:

式中:ρ为流体密度,U为速度矢量。

(2) 动量守恒方程。微元体中的流体动量针对时间的变化率与作用在该微元体上的各种力之和相同。由此可得出动量守恒方程:

式中:μi为i方向流体速度分量,μj为j方向流体速度分量,x i为i方向的位置,x j为j方向的位置,p为静压力,τij为应力张量,g i为i方向上的重力体积力,F i为i方向上由于阻力和能源而引起的其他能源项。

应力张量如式(3)所示:

式中:μ为动力粘性系数,δij为克罗内克函数。

(3) 能量守恒方程。微元体内总能量的变化率与外界作用力对微元体所做功的功率和以导热向微元体传热的功率之和相同[11],对于牛顿流体,能量守恒方程的形式如下:

式中:T为绝对温度,K为传热系数,C P为比热容,S T为粘性耗散项。

1.2 湍流模型

当动车组运行速度为160～350 km/h时,10～30 m/s横风条件下对应的马赫数最大值小于0.3,属于低马赫数流体,可按照不可压缩流体进行计算,此时受电弓周围的空气绕流场可以视为定常、等温、不可压缩的三维流场。流场雷诺数较高,按照湍流处理[12]。本文采用的湍流数值模拟方法为雷诺时均法,是将非稳态控制方程对时间作平均,得到的关于时均物理量的控制方程包含了脉动量乘积的时均值等未知量。本文应用的湍流模型为SSTk-ω模型,该模型结合了k-ω原型和k-ε模型各自的优点,对自由来流的湍流度没有很强的依赖性。相比于k-ω原型,SSTk-ω模 型 在流体分析时能更精确地模拟反压力梯度引起的分离点和分离区的大小。SSTk-ω模型方程如下[13]:

式中:k为湍流动能;v i为流体流速;ω为涡量脉动强度;Γk,Γω分别代表k与ω的有效扩散项;G k为因层流速度梯度而产生的湍流动能;Gω为由ω方程对应产生的湍流动能;Y k,Yω分别代表k与ω的发散项;S k,Sω为用户自定义。

1.3 受电弓气动抬升力等效模型

受电弓结构复杂,含有较多的零部件,因此在力学分析计算时需要运用二维结构建立等效计算模型[14-17]。由于平衡杆和下导杆所受气动力较小,为简化计算,二者的气动力可忽略不计。弓头与上臂杆之间是铰接关系,不存在力矩传递,可将弓头的气动阻力和升力等效至上臂杆顶端。受电弓弓头在外载荷作用时沿垂向运动,因此可在上臂杆顶端施加垂向约束,计算受电弓各组成部件在气动力作用时产生的垂向约束反力,此力与受电弓气动抬升力大小相等、方向相反。受电弓气动抬升力等效模型如图1所示。

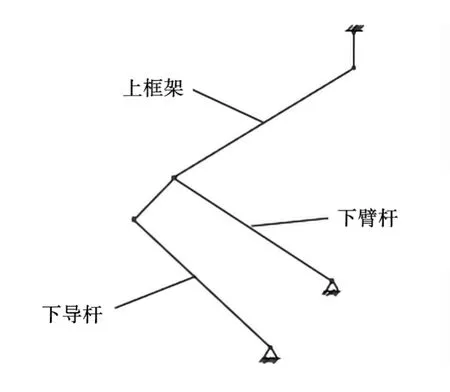
图1 受电弓气动抬升力等效模型

为便于分析计算,需要确立受电弓二维模型的坐标系和角度。如图2所示,将下导杆与受电弓底架的连接点d设为坐标原点,m、n、p分别为上框架、下臂杆、下导杆的气动力等效作用点,α与θ是上臂杆与下臂杆的升弓角度,β与γ分别是上框架bc段、下导杆与水平面的夹角。

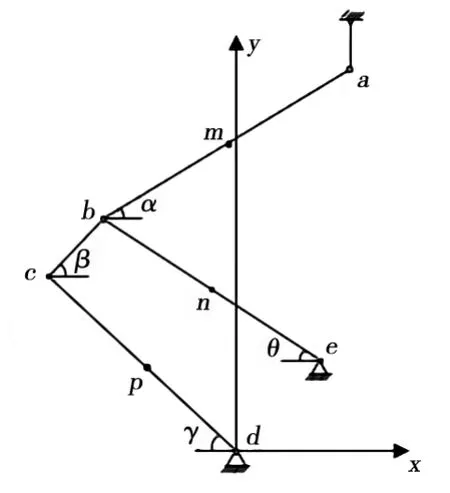
图2 受电弓部件角度及坐标系

1.4 受电弓气动抬升力计算

通过受电弓空气动力学仿真分析可以计算出列车运行过程中受电弓各组成部件所受的气动力,将各部件所受气动力代入到受电弓气动抬升力的等效计算模型,建立力学平衡方程,求解出受电弓气动抬升力的大小。受电弓各部件所受气动力转化为总气动抬升力的影响系数并不相同,求解时需要将各组成部件的气动力往气动力矩为零处等效。受电弓各组成部件受力分析如图3～图5所示。

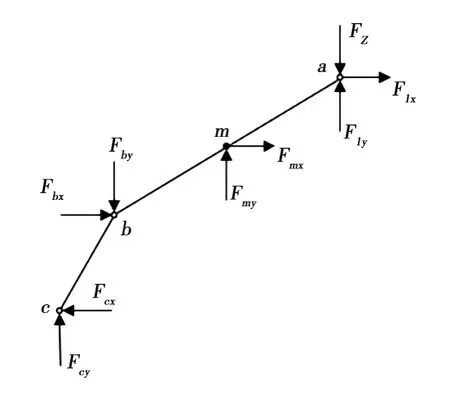
图3 上框架受力分析

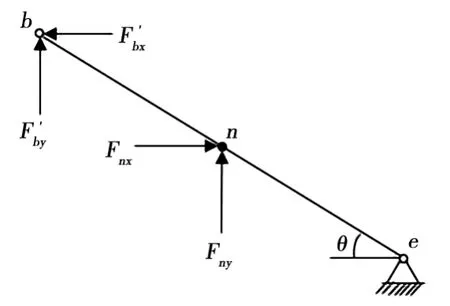
图4 下臂杆受力分析

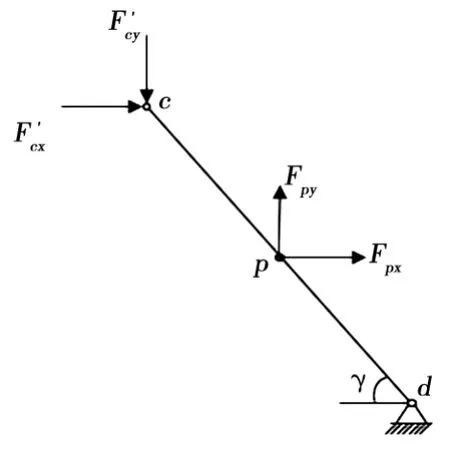
图5 下导杆受力分析

F z为受电弓所受的垂向约束反力,与需要求解的气动抬升力大小相同、方向相反,F1x、F1y、F mx、F my、F nx、F ny、F px、F py分别表示受电弓受气动力影响作用在弓头、上框架、下臂杆及下导杆上的气动升力及气动阻力,F bx、F by表示下臂杆在转铰b处对上框架的作用力,F cx、F cy表示下导杆在转铰c处对上框架的作用力,其余力为上框架在转铰b、c处分别对下臂杆及下导杆的反作用力。对于上框架,根据各力关于x和y方向力平衡且关于b点力矩平衡可得式(7):

对于下臂杆,各力关于e点力矩平衡可得式(8):

同理,对于下导杆,各力关于d点力矩平衡可得式(9):

根据作用力与反作用力的关系以及受电弓的结构尺寸关系可得:=F cx、=F cy、=F bx、=F by,L ab=L am+L bm,L be=L bn+L ne,L cd=L cp+L pd。联立式(7)～式(9)可得力F z的表达式如式(10)所示:

式中:A1、A2、A3、A4、A5、A6、A7、A8分别表示弓头、上框架、下臂杆及下导杆的气动阻力和气动升力转化为气动抬升力的影响系数。

具体表达式如式(11)所示:

当受电弓各部件的角度及气动力的等效位置确定后,即可获得各部件对应的影响系数。将仿真得到的各部件气动力代入式(10),即可得到受电弓气动抬升力,将其与受电弓静态抬升力叠加之后可得到受电弓弓网接触力,然后再与相关接触力标准比较来判断仿真结果的合理性,为后续受电弓的气动特性分析奠定基础。

另外,受电弓弓网接触力主要由气动抬升力和静态抬升力叠加组成,其静态抬升力的大小主要由电流类型决定(AC系统:60～90 N;DC 1.5 kV系统:70～110 N)。EN 50119:2001《电气化铁道接触网设计、施工及验收标准》要求的最大弓网接触力不超过400 N,最小接触力大于零。

2 高速列车及受电弓碳滑板波纹模型

2.1 高速列车气动模型

如图6所示,本文采用sss400+型受电弓进行数值模拟。受电弓主要由弓头、上臂杆、平衡杆、下臂杆、推杆、底架及绝缘子组成。进行数值模拟分析时,需要对受电弓进行简化,将其中影响分析效率且对整体气动特性影响较小的部分进行省略[18-19],以提高模拟仿真效率,简化后的受电弓模型如图7所示。

图6 受电弓实际模型

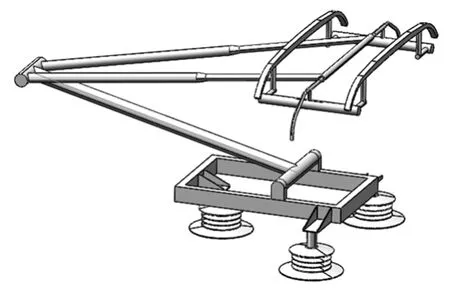
图7 简化后的受电弓模型

受电弓位于车体顶部,在实际运行过程中,在高速气流作用下,车体顶面附近的空气流场对受电弓的流场产生一定的影响,特别是有横风作用时,受电弓及车体周围流场分布变化剧烈。横风对车体表面流场的影响会叠加到受电弓周围流场中,这种叠加作用会显著影响受电弓各部件的气动性能,因此需要对包含3辆编组高速列车的受电弓组合模型进行流场分析。由于车辆间的风挡及车体底部转向架对受电弓的流场影响较小,因此在建立模型时对上述部件进行简化。相关研究表明,受电弓以闭口运行时列车的气动特性优于开口运行,受电弓安装在远离列车运行方向的位置时气动噪声相对较低,由此建立的包含3辆编组的高速列车受电弓组合模型如图8所示。

图8 简化后的3辆编组高速列车受电弓组合模型

2.2 4种碳滑板表面波纹组合模型

国内外针对受电弓气动阻力减小的研究主要基于两方面:一是对受电弓本身结构外形的优化;二是对受电弓的运行流场环境进行改变,例如安装平台高度、导流罩形状及受电弓运行方式等。对于降噪研究主要有2种方式,主动降噪和被动降噪。主动降噪并不改变受电弓本身结构,而被动降噪与此相反。本文基于第1种减阻层面并采用被动降噪方式,在受电弓碳滑板表面设置波纹(图9),为了不影响受电弓弓头与接触网的直接接触,选择在受电弓的迎风侧与背风侧设置波纹。依据波纹不同位置,设置了4种类型的受电弓组合模型,如图10所示。波纹数量为10,每段波纹(1个周期)长度为62 mm,幅值为13 mm。

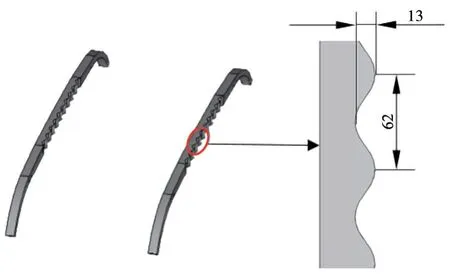
图9 表面含有波纹的受电弓弓头

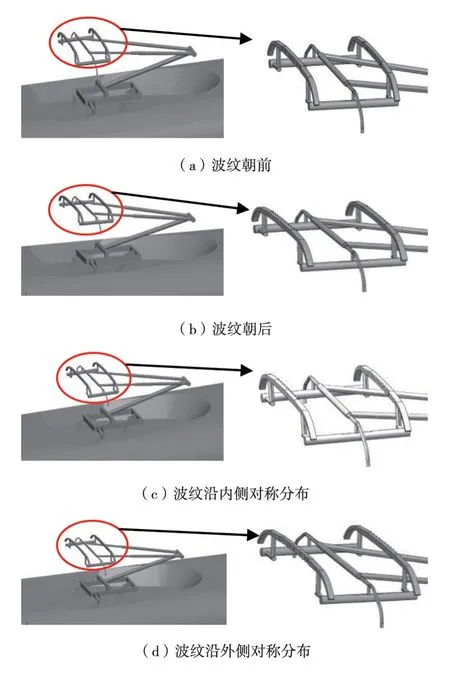
图10 4种受电弓碳滑板表面波纹组合模型

3 高速列车气动流场模型

3.1 计算域及网格划分

高速列车受电弓的实际空气流场环境是无限大区域,但是数值计算难以实现建立无限大的外流场区域。实际上,只要设置足够大的计算域,避免边界出现明显的回流影响受电弓的流场分布,保证受电弓流场充分发展即可。受电弓与3辆编组高速列车组合模型计算域如图11所示,长×宽×高为267 m×192 m×34 m。

图11 计算域尺寸及边界设置(单位:m)

对于包含3辆编组高速列车的受电弓这一复杂组合模型,本文采用非结构化网格进行划分。为了获得更加准确的受电弓流场分布及气动特性结果,本文在受电弓及车体表面附近进行了网格加密处理,并在列车及受电弓表面设置了边界层,受电弓壁面附近首层边界层高度为0.1 mm,层数设为8层,边界层总厚度为4.3 mm,如图12所示,对于无波纹的受电弓组合模型最终划分的网格数为8 986 492。

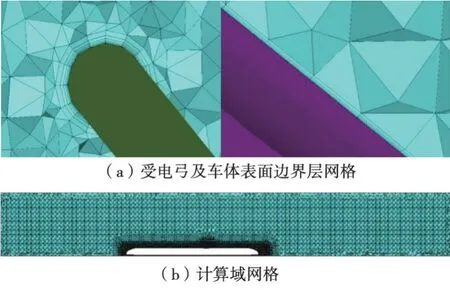
图12 网格划分结果

3.2 边界条件求解设置

对受电弓组合模型及单个受电弓模型进行数值模拟仿真时,计算域的各个面都需要单独设置以便后期加入具体的边界参数更加接近实际运行情况。如图11所示,利用ICEM CFD 将各个面单独设置为入口、出口、侧面入口、侧面出口、地面及顶面。

高速列车实际运行过程中,受电弓与周围空气流体发生相对运动,在对物体进行绕流场分析时,一般对流体介质赋予一定的速度而使仿真分析表面保持静止不动。因此在Fluent软件中,利用相对运动原理,假设受电弓组合模型静止不动,空气以列车运行速度大小从入口处吹入,从出口处流出。由于本文分析流场属于不可压缩流场,则入口为速度入口,速度与列车运行速度一致,出口为压力出口,压力为一个标准大气压。受电弓及列车表面为固定壁面,受电弓实际运行时与地面间存在相对运动,因此需要将地面设置为移动地面,移动速度与列车运行速度相同,移动方向与列车运行方向相反。当有横风存在时,侧面边界条件设置为速度入口和压力出口,当无横风时,侧面边界条件设置成与顶面同样的对称边界条件。

本文基于分离式求解器,利用有限容积法数值模拟受电弓的流场分布,运用二阶迎风格式建立离散方程,控制方程经过离散后运用SIMPLEC方法求解计算。

4 不同受电弓组合模型的气动特性

4.1 受电弓组合模型气动力分析

为了分析受电弓碳滑板迎风及背风表面波纹位置对受电弓气动特性的影响,分别计算了4种含有波纹的受电弓组合模型及无波纹的受电弓组合模型在列车运行速度350 km/h、横风风速15 m/s及风向角90°的工况下受电弓各组成部件的气动力,并且根据受电弓接触力计算公式得到了整个受电弓的气动抬升力(表1)。受电弓的底架及绝缘子固定在列车顶面,其受到的气动升力主要来自于底架以上结构。由表1可以得出,上述受电弓组合模型的弓网接触力均满足规定要求。其中,弓头的气动阻力占比最大,在55%以上;其次是底架及绝缘子组件,气动阻力占比在27%及以上;当碳滑板表面无波纹时,底架及绝缘子组件的气动阻力最大且占比高达31%。这些数值表明,在受电弓碳滑板上增加波纹结构有助于降低底架及绝缘子的气动阻力,且不论波纹处于什么位置,受电弓的气动阻力相比于无波纹时的气动阻力都有所下降。波纹朝前时对应的受电弓的整弓气动阻力最小,减小了约9.3%。波纹结构对碳滑板自身的阻力影响较小,数值波动范围在2.8%以内,但对弓头其余组件的气动阻力影响较大,最大减少约10.2%,对上臂杆及下臂杆气动阻力影响也较大,最大减少15.5%和17.0%。受波纹结构影响最大的是绝缘子及底架结构,其气动阻力最大减少21.1%。

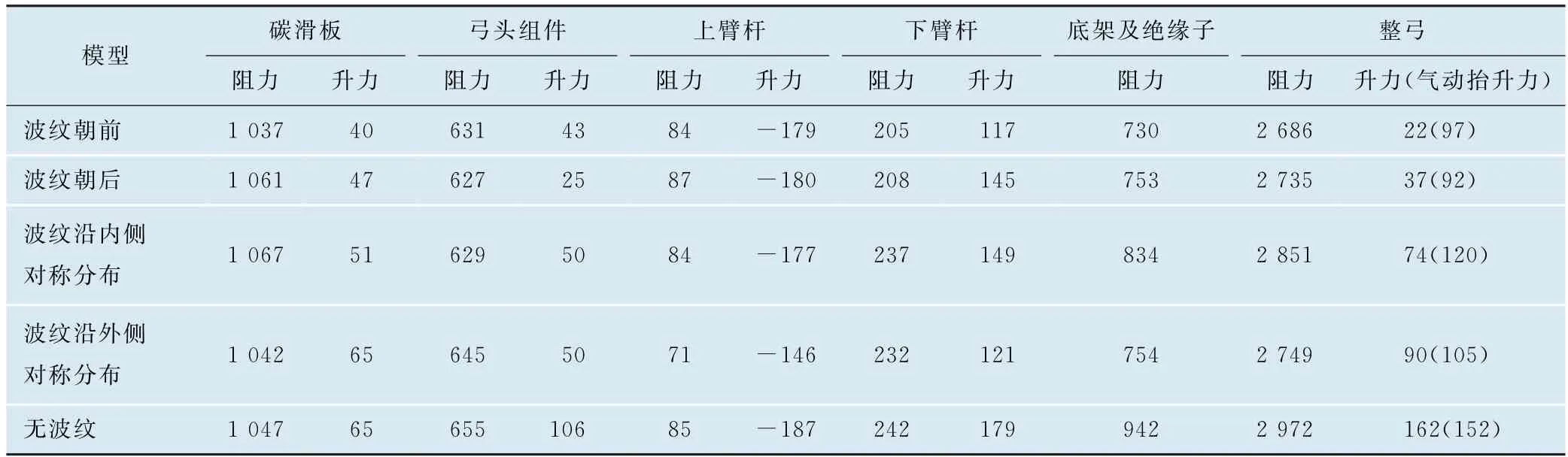
表1 不同受电弓组合模型对应组成部件气动载荷(含整弓气动抬升力)N

4.2 速度云图对比分析

本文设置了4种运行速度工况,分别是200 km/h、250 km/h、300 km/h和350 km/h,其横风速度及风向角均为15 m/s和90°。利用稳态流场分析得到4种工况下不同受电弓组合模型的速度云图。由于各受电弓组合模型随运行速度变化的趋势相同,因此只选取波纹沿外侧对称分布的组合模型进行不同速度下的对比分析,如图13所示。

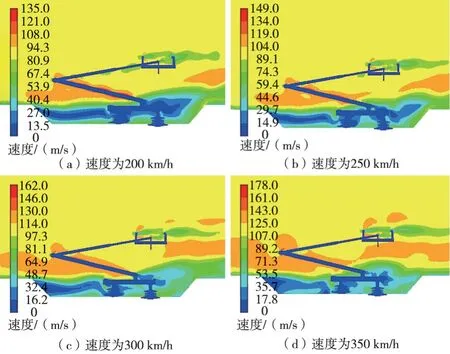
图13 不同运行速度下流场对比分析

从图13可以得出,当气流以较高速度流过受电弓时,会在弓头附近发生分离现象,使得背风侧气流速度显著下降,从而在弓头表面形成较大的压差阻力。由于前碳滑板尾流涡的作用,导致后碳滑板迎风侧的气流速度显著降低,即后碳滑板的表面压差较前碳滑板而言较小。表面压差大小决定气动阻力大小,因此受电弓碳滑板气动阻力大小主要由前碳滑板决定。车顶导流罩附近的气流在流过导流罩时也发生了分离,一部分形成了低速漩涡,作用于绝缘子迎风面,使得正压有所降低,另一支气流保持基本不变的速度流过底架。

从图13还可以得出,随着列车速度的增加,同种模型弓头尾流区面积及尾流涡脱落程度也逐渐增加,且前碳滑板边界层分离区位置逐渐前移,导致碳滑板表面压差逐渐增大,即气动阻力逐渐增大。同一模型的导流罩、受电弓底架及绝缘子的低速尾流区范围逐渐减小。

当列车运行速度为350 km/h时,各组合模型下的受电弓流场如图14所示,各组合模型碳滑板流场如图15所示。由图14和图15可得,含有波纹结构的受电弓的底架及绝缘子迎风侧风速相比于无波纹模型较小,背风侧风速大小基本相同,特别是绝缘子,表面来流风速较大时所对应的压力也较大。因此含有波纹的结构,其底架及绝缘子气动阻力较无波纹结构而言较小。波纹朝前及波纹沿外侧对称分布的受电弓组合模型对应的碳滑板的边界层分离区的位置,较无波纹、波纹朝后及波纹沿内测对称分布的受电弓组合模型相对靠后,因此对应的碳滑板气动阻力较小。

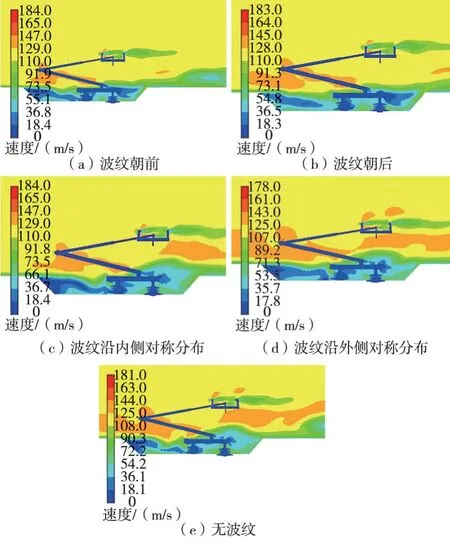
图14 350 km/h各组合模型流场对比分析

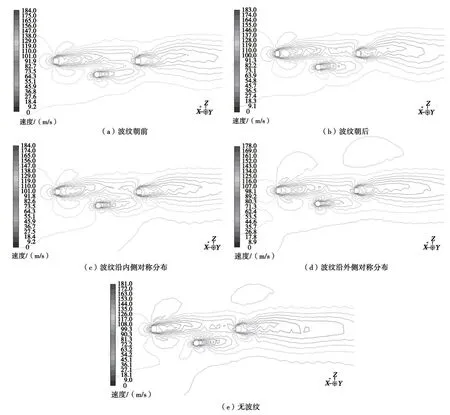
图15 350 km/h下各组合模型碳滑板流场对比分析

由图15可知,前碳滑板波纹朝前时,气流的扰动程度降低,边界层分离区的位置后移使得气动阻力降低。波纹朝后或波纹沿内侧对称分布时,受电弓弓头的尾流区面积较无波纹模型大,且漩涡的脱落程度增加,边界层分离区的位置与无波纹模型基本相同,因此弓头的气动阻力比无波纹模型大。因此,前碳滑板波纹朝后时,碳滑板尾流区面积增大使得气动阻力增加且气流扰动程度增加。波纹对称分布时,碳滑板流场对弓头组件流场影响较大,使得弓头组件尾流涡面积增大,尾流涡脱落程度增加,导致表面压差及气动阻力增大。

4.3 压力云图对比分析

由于不同受电弓组合模型在4种运行速度工况下的压力变化趋势一致,因此选取波纹朝前受电弓组合模型的压力云图进行对比,结果如图16所示,图中的左侧对应受电弓迎风侧的压力云图,右侧对应受电弓背风侧的压力云图。

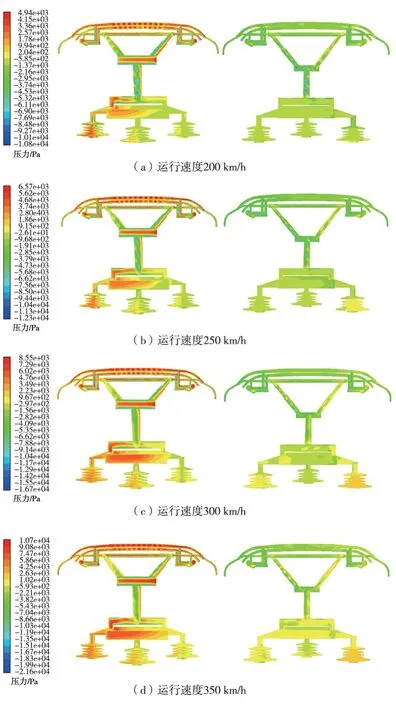
图16 不同运行速度下压力云图对比

由图16可得,随着列车运行速度增加,受电弓组件表面的迎风侧与背风侧的压力均逐渐增加,但迎风侧的压力增加速度大于背风侧,因此受电弓表面的气动阻力逐渐增加。由于横风的存在,受电弓的压力作用方向都与受电弓对称面存在一定夹角,正压较大处均位于弓头迎风侧、上下臂杆铰接处、底架及绝缘子迎风侧。

不同波纹位置的受电弓组合模型与无波纹受电弓组合模型在350 km/h运行速度下的压力云图如图17所示。从图17可以得出,无波纹受电弓组合模型对应的底架及绝缘子正压最大,负压相对较小。与无波纹的受电弓组合模型相比,波纹沿内侧对称分布的受电弓底架及绝缘子的正压较小,负压较大,因此无波纹模型对应的底架及绝缘子气动阻力最大,其次是波纹沿内侧对称分布的模型对应的气动阻力较大。

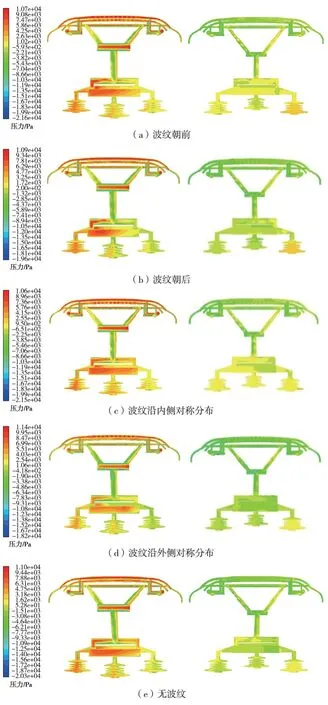
图17 350 km/h下各组合模型压力云图对比

4.4 不同速度受电弓组合模型气动力对比

4种不同受电弓组合模型下的受电弓所受气动升力及气动阻力随列车运行速度的变化如图18和图19所示,其中横风风速15 m/s,风向角90°。由图18和图19可见,列车运行速度为250～350 km/h时,除无波纹受电弓组合模型外,其余含有波纹的受电弓组合模型的气动升力基本均随运行速度的增加而减小。在速度为200～250 km/h时,除波纹朝前的受电弓组合模型之外,其他模型的气动升力均随列车运行速度的增加而增加。整体上看,列车高速运行时波纹朝前模型所受气动升力相对较小。受电弓气动阻力基本随列车运行速度的增加呈线性增大的趋势,在速度为200～300 km/h时,波纹位置不同的各组合模型气动阻力相差较小(在3%以内),当运行速度为350 km/h时,波纹位置不同的各组合模型的气动阻力大小差异增大,最大达到6%。随着列车运行速度的增加,含有波纹结构的受电弓组合模型的气动阻力小于无波纹模型的趋势愈发显著。

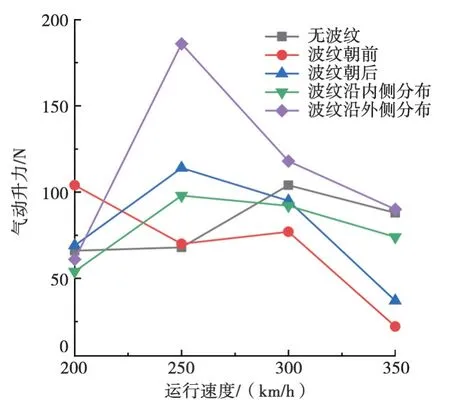
图18 气动升力变化曲线

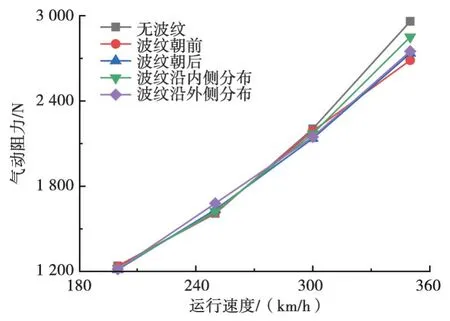
图19 气动阻力变化曲线

5 结论

本文建立了包含单个受电弓和3辆编组高速列车的受电弓组合模型,并且在受电弓碳滑板上增加了波纹结构,对比分析了4种碳滑板表面波纹位置不同的受电弓组合模型与无波纹受电弓组合模型的定常气动特性,结论如下:

(1) 对于碳滑板波纹位置不同的4种受电弓组合模型,波纹朝前受电弓组合模型对应的气动阻力最小,相比于无波纹受电弓组合模型减小了9.3%,列车运行速度为350 km/h时,相比于前碳滑板波纹朝后及无波纹受电弓组合模型,前碳滑板波纹朝前模型对应气流的扰动程度降低,边界层分离区的位置后移使得气动阻力降低。

(2) 前碳滑板波纹朝后时,相比于无波纹模型,碳滑板尾流区面积增大使得气动阻力增加且气流扰动程度增加。波纹对称分布时,碳滑板流场对弓头组件流场影响较大,使得弓头组件尾流区面积增大,表面压差增大,气动阻力增大。

(3) 列车高速运行时,波纹朝前模型所受气动升力相对较小。含有波纹结构的受电弓组合模型的气动阻力小于无波纹模型的趋势随速度的增加愈发明显。