模糊曼哈顿距离加权最优粒度选择算法
2023-10-27李璐李宝霖李丽红
李璐,李宝霖,李丽红
(1. 华北理工大学 理学院,河北 唐山 063210;2. 河北省数据科学与应用重点实验室,河北 唐山 063210;3. 唐山市数据科学重点实验室,河北 唐山 063210)
引言
粒计算理论起源于信息粒概念,1979年由Zadeh[1]提出,简化处理抽象复杂问题,一经提出便成为热点。粒计算的确切概念是在1996年由Lin[2]提出,该理论的面世标志了一种多角度分析处理问题的方法产生,有助于更好地给出解决问题方案。Lin[3]随后完善了该理论,并讨论了其发展前景与方向,其中指出粒计算理论中,如何划分粒层以及粒层的选择问题是重中之重,国内外专家学者也对此进行了深入的讨论。吴伟志等[4]讨论了在不完备多粒度决策系统中如何找寻最优粒度。刘凤玲[5]提出了在现实背景下的多粒度信息系统如何找寻最优粒度。李金海[6]将信息熵融合作为找寻最优粒度标准。
三支决策思想与中国传统中庸思想有着不可分割的联系,"中"被理解为"适当",决策思维符合人类思维方式,三支决策后样本被分到3个域中,对不同的部分采用不同的处理策略,分别采取接受、延迟和拒绝行为。三支决策与粒计算融合发展是必然的,研究目标是将问题分解为多个角度、多个层次进行思考,三支决策模型的拓展模型之一是序贯三支决策模型。序贯三支决策[7,8]从粒计算角度出发,由粗粒度转化为细粒度解决问题,延迟域中对象进一步被决策,在医学、图像、工程、属性约简、管理等方面已有广泛应用[9,10]。顾沈明等[11]在多尺度信息系统中利用属性及局部最优得到广义决策最优粒度。Yang等[12]通过优化得到基于代价敏感的序贯最优粒度。Cheng等[13]基于序贯三支决策快速获取最优尺度组合,李敏等[14]基于代价变化,引入可拓集方法,结合三支决策思想提出最优粒度选择模型,张清华等[15]提出基于惩罚函数并结合序贯三支决策的最优粒度选择方法。
现有最优粒度选择方法大多在信息系统中利用静态指标度量信息,如利用重要度方法选择来看,存在数据冗余或未考虑各属性间关系的问题。其次存在多使用一般性数据集,未能更符合实际应用场景的问题。为此,本研究提出了一种粒化空间下基于模糊曼哈顿距离加权的个性化最优粒度选择方法。它实际上是一个三级结构,采用三支决策的三级思维方式。具体来说,它首先结合隶属函数与曼哈顿距离,定义了模糊曼哈顿距离来重新计算属性间的关联程度;然后,放弃使用手动编辑的粒度,而利用自身属性距离空间产生的数据粒化,可以减少手动编辑粒度所导致的随机性、不确定性甚至冗余。最后,分析数据分类结果,以其作为粒度选择基础,验证算法有效性,实现对数据的最优粒度选择,并以同物不同级数据作为实验数据,验证算法的可行性,将为样本选择可优化的最优粒度提供一种新的思路。
1 相关知识
1.1 三支决策
三支决策是将论域通过阈值划分为独立的三部分,每一个部分采取相应的行动,若样本条件概率值大于上近似阈值,则划分到接受域中;若其小于下近似阈值,则划分到拒绝域中;若其在值域范围内,需要等待更多信息对样本做出判断,则划分到延迟域中。
定义1[16]给定信息系统S=(U,AT,V,f),U是论域,即需要处理的样本对象,AT代表属性集,是有限集合,C是条件属性,D是决策属性,V是属性AT的值域,f:U×AT→V是一种映射,对于a∈AT,x∈U,f(x,a)∈Va,任一子集满足φ≠H⊆AT,则在U上的等价关系为id(H)={(x,y)∈U×U|f(x,q)=f(y,q),∀q∈H}。
定义2[17]给定信息系统S=(U,AT,V,f),λPP,λBP,λNP为样本属于决策类并且被分到正域、边界域、负域时的决策风险代价,λPN,λBN,λNN为样本不属于决策类并且被分到正域、边界域、负域时的决策风险代价。当样本x属于决策类时,其条件概率为P(X|x)=p,此时样本x划分到3个域的决策风险代价分别是:
正域:λPPp+λPN(1-p),边界域:λBPp+λBN(1-p),负域:λNPp+λNN(1-p)
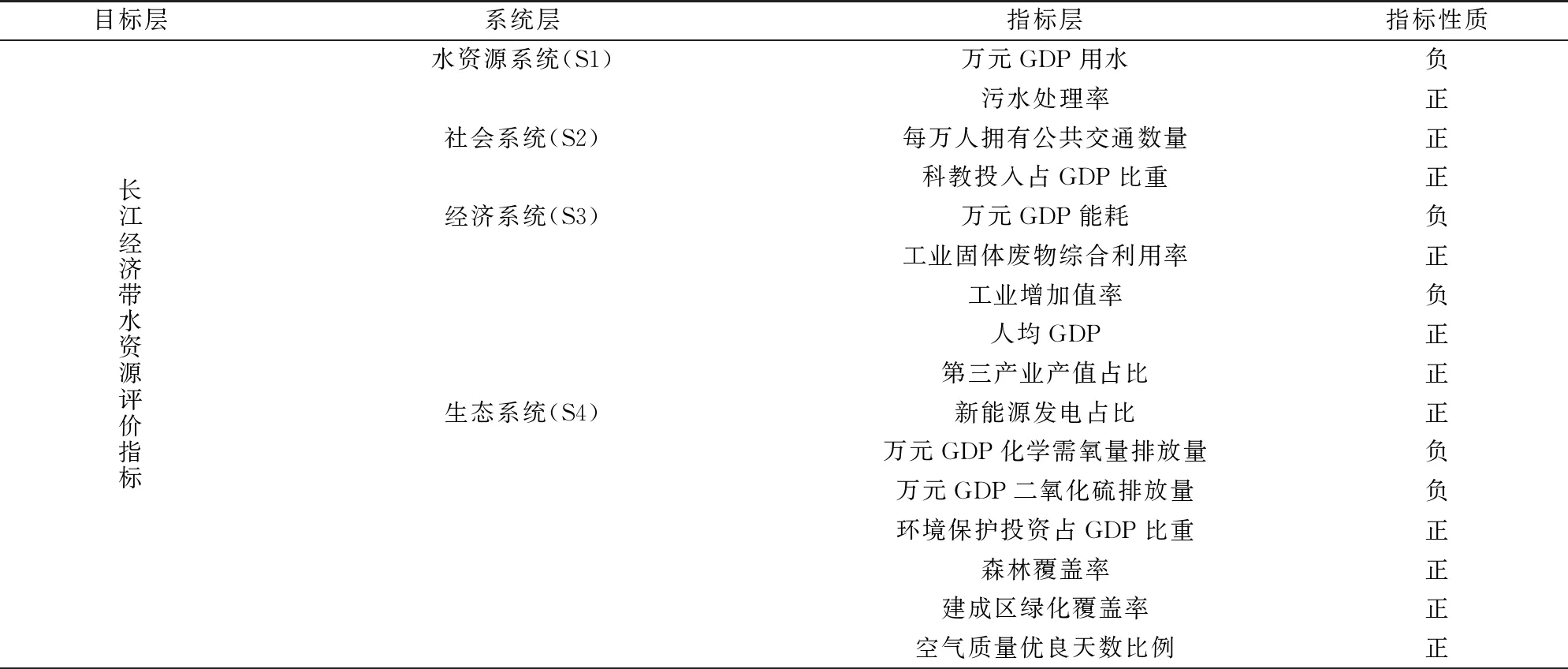
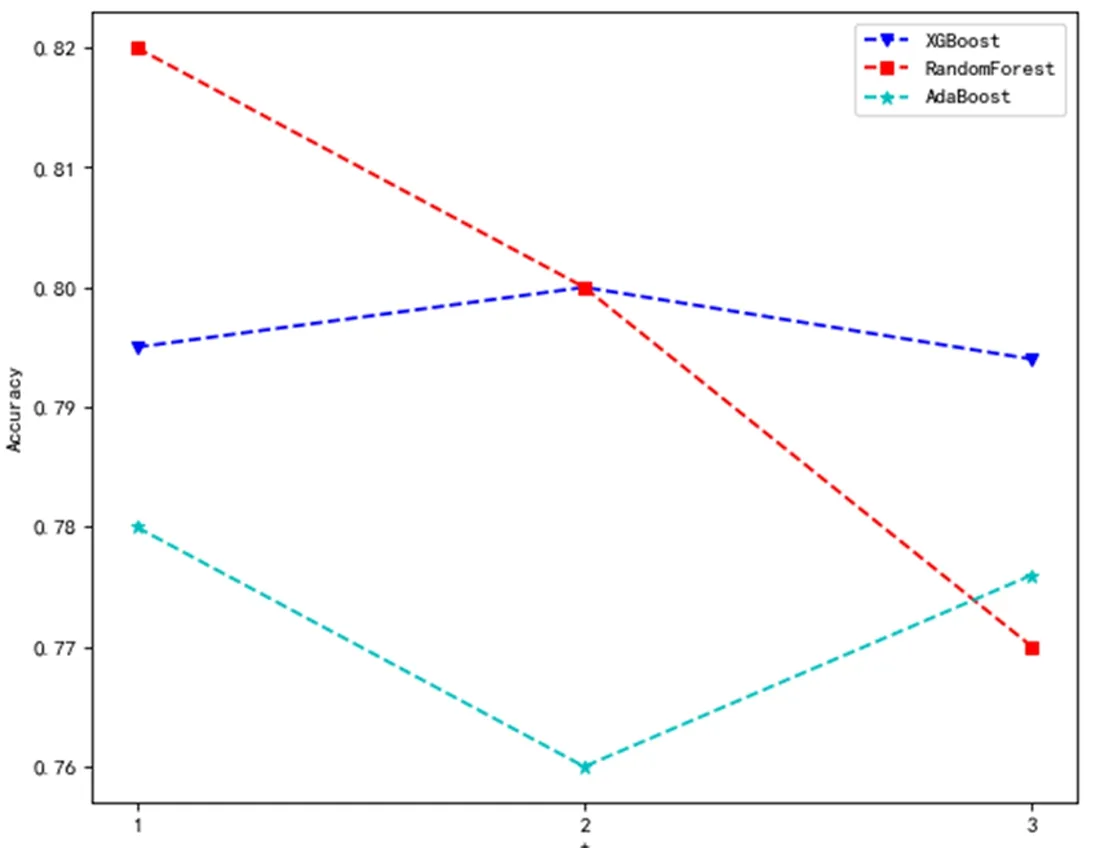
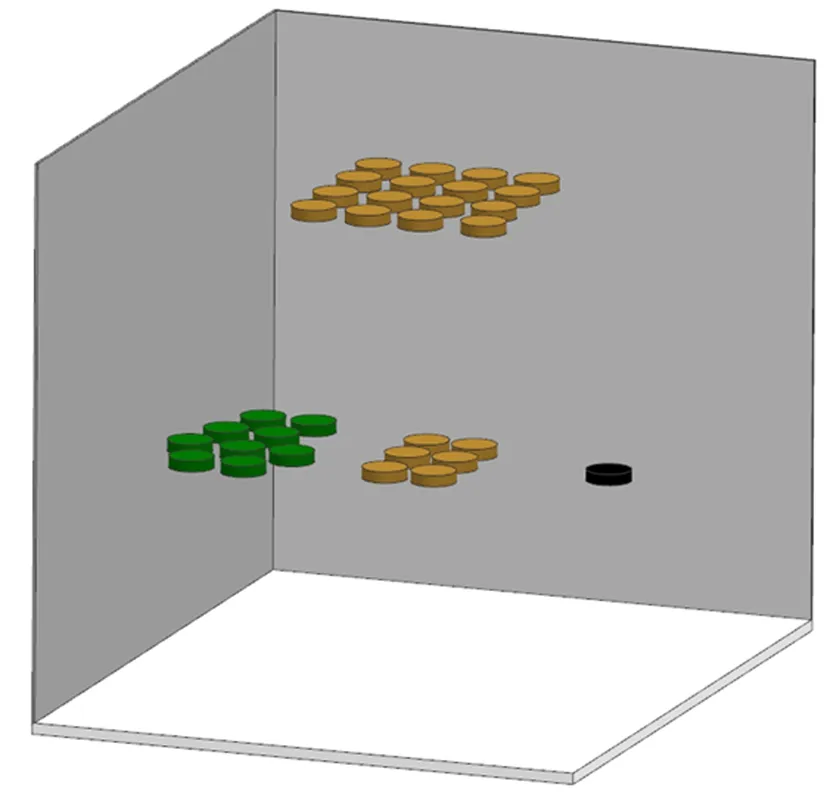
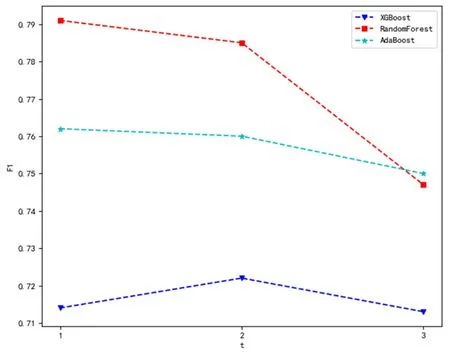
定义3[17]给定信息系统S=(U,AT,V,f),设状态空间Θ=(D,D),表示对象x是是否属于集合D,样本xi属于决策类D的条件概率为样本构成的所有概率集合为P,当P(X|xi)=pi≥α时,样本xi∈P1,即接受域;当β 由于P(X|x)+P(X|x)=1,λPP=λNN=0,同时λPP<λBP<λNP,λNN<λBN<λPN,(λPN-λBN)(λNP-λBP)>(λBP-λPP)(λBN-λNN),即: (1) (2) 广义三支决策的概念被适时提出[18]针对的则是更加复杂、不确定和动态的数据集,相比于狭义,后者更强调对原有概念更深层次、更广范围的诠释。二者联系如图1所示。 图1中以垂直结构直观地展示出了三支决策整体脉络。从上到下,代表由广至狭的三支决策;自下而上,由静而动的三支决策。在现实中,决策分析一开始获得的信息往往是不充分的,决策需要信息的更新和补充,由此序贯三支决策的概念被提出。 曼哈顿距离中的距离计算公式是将两点坐标的 坐标相减取绝对值, 坐标相减取绝对值后再加和,用以度量样本的相似程度。模糊集合描述的对象属性边界不分明,这一概念用于处理模糊性现象,被广泛应用到数据预处理中。 定义4[19]设U为论域,U上的一个模糊集A表示∀x∈U,有指定数μA∈[0,1],则称x对A的隶属程度,映射μA:X→[0,1],x→μA(x)称为A的隶属函数。设T(X)表示X上的一切模糊子集集合,则T(X)是由μ:X→[0,1]组成的函数空间。 定义5给定一个信息系统S=(U,AT,V,f),其中:AT=C∪D,C代表条件属性集,D代表决策属性集。在n个样本中,μi(m)为第m个样本在属性i上对应的隶属度,d(i,j)表示属性i与属性j间距离。定义属性间模糊曼哈顿距离: (3) 数据集所包含的有效信息如表1所示。 表1 信息系统 数据集中有多个指标,该算法实施以属性权重为基础粒化,构建粒层空间。下面将介绍具体步骤。 Step1:计算属性重要度 步骤一:指标标准化处理 由于各指标量纲不同,且指标有正负之分,正负代表含义不同,正向指标数值越高越好,反之越低越好。因此为统一计量单位,对数据标准化处理。 其中,x*(i,j)为第i个样本第j个评价指标值,xmax(i,j)为所有样本中第j个评价指标最大值,xmin(i,j)为所有样本中第j个评价指标最小值。 步骤二:熵权法计算属性重要度并输出 Step2:计算属性间关系 步骤一:对原始数据模糊化处理 (4) a是样本集中各属性的最小值,得到各属性模糊隶属度和消除量纲的矩阵。 Step3:构建粒空间 根据模糊矩阵R,构建有序样本的粒空间,即根据d(i,j)的大小依次聚类,依据属性重要度和距离加权,构建粒层。 粒计算以粒为基本单位,可利用属性指标划分得到不同粒层。该项研究采用模糊思想将数据模糊化处理后,构建不同层次空间,描述属性或样本之间的等价关系,应用多种算法框架分析分类结果,获得最佳粒层空间上的优化指标。算法步骤 Step1:依据上述方法得到属性模糊距离矩阵R。 Step2:构建粒层,首先在待分属性中选取属性重要度最低属性放于拒绝域;其次选取与重要度最高属性的距离从小到大计算平均重要度,选取平均重要度最高的距离,构建分类模型,将属性放入接受域中;其余属性放入延迟域。 Step3:将延迟域中属性继续按上述步骤构建层次粒空间,分别用精确率、召回率及F1值检验所选择的最优粒度,用以佐证其有效性。 仿真实验环境为:Python编程; 硬件环境:Intel(R) Core(TM) i5-10210U;16GB; 软件环境:操作系统:Windows 10 家庭中文版; 解释器:Python3.8,使用Python编程。 以长江经济带省级行政区为研究区,综合分析后选取16个指标,如表2所示。其中,指标性质为"正"代表指标为正向指标,指标值越大越好;指标性质为"负"代表指标为负向指标,指标值越小越好。 表2 长江经济带水资源评价指标 (1)指标标准化处理后,根据熵权法计算属性重要度排序,结果如表3所示。 表3 属性重要度排序 (2)计算各属性间模糊曼哈顿距离,建立模糊矩阵R。 (3)第一次循环时在待分属性中选取属性重要度最低的"建成区绿化覆盖率"属性放于拒绝域;选取与重要度最高属性的距离从小到大计算平均重要度,本次选取平均重要度最高的距离为1.926,得到属性"万元GDP用水"、"每万人拥有公共交通数量"、"新能源发电占比"、"工业固体废物综合利用率"、"城市污水处理率"、"工业增加值率"、"第三产业产值占比"、"森林覆盖率"、"空气质量优良天数比例"放入接受域中,以不同算法为分类工具,构建分类模型计算准确率;其余属性放入延迟域。 (4)第二次循环时在待分属性中选取属性重要度最低的"万元GDP化学需氧量排放量"属性放于拒绝域;选取与重要度最高属性的距离从小到大计算平均重要度,本次选取平均重要度最高的距离为3.924,得到属性"人均GDP"、"科教投入占GDP比重"放入接受域中,以不同算法为分类工具,构建分类模型计算准确率;其余属性放入延迟域。 (5)第三次循环时在待分属性中选取属性重要度最低的"万元GDP能耗"属性放于拒绝域;选取与重要度最高属性的距离从小到大计算平均重要度,本次选取平均重要度最高的距离为3.786,得到属性"万元GDP二氧化硫排放量"放入接受域中,以不同算法为分类工具,构建分类模型计算准确率。 根据每一轮选择的接受域属性,以ADABOOST、XGBOOST、随机森林3种算法构建分类模型计算准确率,得到分类结果,证明其可行性。如图2所示,纵坐标为准确率,横坐标为循环次数。 图2 长江经济带水资源准确率 由图2准确率可知,三个算法下整体准确率达到0.8,验证了算法的有效性,当t=1时3个算法分类准确率均为最高值,因此选择第一粒层作为最优粒层,此时接受域中的属性为待优化属性。 图3直观展示出不同粒度下所需优化的属性个数变化情况,黄色表示待决策属性个数,绿色表示待优化属性个数,黑色表示拒绝域中属性个数。 图3 长江经济带水资源需优化属性变化情况 综合3个学习算法反应结果,在第一次循环后准确率相对较好,此时再次通过F1值对分类结果进行验证,证明其有效性。通过图4对F1值走势分析,XGBoost算法下F1值整体波动不大,AdaBoost、随机森林算法下第一轮结束后F1值最高,综上选择第一粒层为最优粒层,当前粒层属性为待优化属性。 图4 长江经济带水资源数据F1值 综合图中数据显示,第一次循环结束后分类精度普遍较高,验证了算法的有效性。所以对于优化长江经济带发展战略在"控污"方面,可以优化的指标有万元GDP用水量、工业增加值率、人均拥有公共交通数量、新能源发电占比、工业固体废物综合利用率、城市污水处理率、第三产业产值占比、森林覆盖率和空气质量优良天数比例。 (1)利用属性间关系选择粒度,结合模糊曼哈顿距离构建层次粒层空间,可以有效节约时间成本,且可降低对分类结果的影响。 (2)基于模糊曼哈顿距离加权最优粒度选择算法在保证数据完整的前提下为满足不同用户的不同需求,针对不同类别,控制一定成本的情况下,做到对数据的全方面优化提升,从决策系统中获取最优粒度。但该项研究未体现序贯过程中代价变化,因此如何自动获取决策过程代价变化确定最优粒层是未来研究方向。1.2 广义三支决策
1.3 模糊曼哈顿距离
2 粒化空间构造

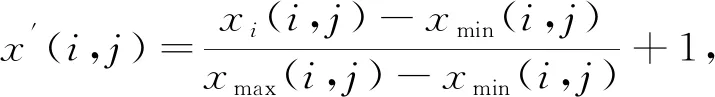
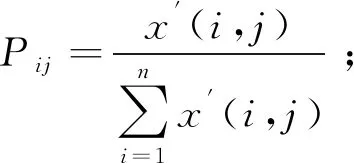
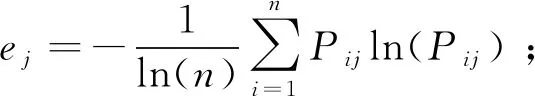

3 模糊曼哈顿距离加权最优粒度选择算法
4 仿真与应用
4.1 实验准备
4.2 案例分析

5 结论
