道路网多用户偏好Top-k 天际线查询方法

李 松 宾婷亮 郝晓红 张丽平 郝忠孝

（哈尔滨理工大学计算机科学与技术学院 哈尔滨 150080）

天际线（Skyline）查询[1]作为多目标决策、兴趣点发现、推荐系统等领域关键问题的一种解决途径，在2001 年被提出，自此受到研究学者的广泛关注与研究.近些年，Skyline 查询研究拓展到不确定数据Skyline 查询[2]﹑数据流Skyline 查询[3]﹑动态Skyline 查询[4]﹑反Skyline 查询[5]、偏好Skyline 查询等方面，其中偏好Skyline 查询可以返回满足用户偏好需求的结果集.针对因用户偏好不同导致属性的重要性不同问题，研究者们提出了新的支配关系与算法.但已有研究主要集中在非道路网的用户偏好Skyline 查询或者道路网单用户偏好Skyline 查询方面，没有考虑道路网多用户偏好和权重的Top-kSkyline 查询.

传统偏好Skyline 查询算法主要存在3 点局限性：1）偏好Skyline 查询需要确定属性的重要程度，由于不同用户权重与偏好不同，因此不同属性的重要程度也不一致，而已有研究中较少有提出将用户偏好和权重综合考虑，得到对用户群统一的属性重要程度次序处理方法；2）传统偏好Skyline 查询算法大多未考虑道路网环境下的距离维度，只考虑静态维度；3）传统偏好Skyline 查询算法返回的结果集过大、无序，不能给用户提供有效的决策支持.

因此，针对道路网多用户偏好Top-kSkyline 查询问题，本文提出满足多用户不同权重和偏好需求的查询方法.

本文的主要贡献有3 点：

1）针对道路网存在大量数据点以及多查询用户场景，需要计算数据点到各个查询用户的道路网距离，从而产生的很大距离计算开销，为了提升距离计算效率，本文根据所提的Vor-R*-DHash 索引结构以及数据点与查询用户群的空间位置关系，提前剪枝在距离维度被支配的大量数据点.

2）针对在道路网Top-kSkyline 查询处理时未综合考虑多用户不同权重和偏好以及返回的结果集数量不可控的问题，本文首先提出整体属性权重值的概念，综合考虑用户权重和偏好；并进一步提出用户群权重偏好次序，并基于此次序提出一种新的支配，即K-准放松支配；接着根据偏好次序进行逐次放松支配，使返回结果集大小可控；同时当k值改变时，动态调整放松轮次即可获取候选结果集CS，而无需重新计算距离、偏好次序等，减少了查询计算开销.

3）针对Skyline 查询返回结果集无序的问题，本文基于z-整体属性权重值，提出了选取Top-k个结果集的打分函数，对候选结果集CS打分排序，返回有序结果集.

1 相关工作

Skyline 查询主要分为集中式查询和分布式查询.其中集中式查询主要分为使用索引结构和不使用索引结构.使用索引结构的算法常用R-tree 等索引结构，例如文献[6]利用最近邻（nearest neighbor，NN）算法和R-tree 索引查找Skyline 点，基于R-tree 可以快速判断数据点是否为Skyline 点，接着利用数据点进行子集合的划分，递归查找Skyline 点.不使用索引结构的Skyline 查询算法主要有基于排序的SFS（sort-filter Skyline）算法[7].而Skyline 查询在不断发展过程中又产生了许多变种问题，例如K-支配空间Skyline 查询[8]﹑连续Skyline 查询[9]﹑针对推荐系统的范围障碍空间连续Skyline 查询[10]﹑概率Skyline 查询[11]以及Top-kSkyline 查询等[12-13].

在集中式计算环境下，文献[14]根据用户不同偏好提出了维度不确定的定义，根据维度特征划分数据，进行Skyline 概率支配测试，同时利用阈值处理大规模数据集Skyline 查询问题.文献[15]提出一种高效偏序域Skyline 查询处理方法，利用倒排索引进行Skyline 查询.在并行计算环境下，文献[16]提出了不完全数据集的偏好Skyline 查询算法SPQ（Skyline preference query）.文献[17]根据用户的偏好，基于Voronoi 图将数据对象划分到不同网格中，并行计算所有对象组合，获取动态Skyline 结果.文献[18]提出了MapReduce 下Top-kSkyline 偏好查询.

道路网Skyline 查询近些年来也受到越来越多的关注.道路网Skyline 查询既考虑数据点的路网空间属性，又考虑非空间属性.文献[19]提出了基于范围的移动对象连续Skyline 查询处理方法，利用Voronoi图组织道路网中的数据点，通过所提的3 种算法减少道路网产生的相交节点数和距离计算开销.文献[20]提出了道路网环境下综合考虑空间距离和社交距离的Skyline 组用户查询方法.

Top-kSkyline 查询在多目标决策中往往更具优势，因为它可以控制返回的结果集数量.文献[21]提出基于安全区域技术解决连续Top-kSkyline 查询结果更新问题，提出了结合Top-k查询和Skyline 查询的安全区域构建算法.文献[22]提出了MapReduce环境下Top-kSkyline 处理方法.文献[23]将K-Skyband查询与Top-kSkyline 查询结合处理大数据集的Top-kSkyline 查询.

目前道路网环境下Top-kSkyline 查询研究大多集中在单用户场景，较少考虑多用户偏好和权重不同的场景.针对已有方法的不足，本文利用查询点与数据点的位置关系剪枝数据集，利用所提的K-准放松支配控制结果集数量；利用所提的打分函数返回有序结果集，在理论论证和分析基础上提出了道路网多用户偏好Top-kSkyline 查询方法.

2 主要定义

设道路网环境下数据集P={p1,p2,…,pn}，查询用户群G={q1,q2,…,qm}.

定义1.道路网距离支配.给定查询用户群G、数据点p1、数据点p2，数据点之间的距离为Dist，当且仅当Dist（p1,qi）≤Dist（p2,qi），1≤i≤m；且存在Dist（p1,qi）＜Dist（p2,qi），1≤i≤m，称p1道路网距离支配p2，记作p1►p2.本文距离如不特殊说明，则为道路网距离.

定义2.整体属性权重.给定查询用户群G，用户权重w={w1,w2,…,wm}，用户qi的查询关键字keys={C1，C2}，C1为优先考虑的属性集合，C2为一般偏好的属性集合，任意维度dj的整体属性权重Wj如式（1）：

其中si代表属性dj对于用户qi的重要性得分.

在属性的重要性程度计分时，将属性偏好分为3 类：优先考虑﹑一般偏好和未考虑.不同类别分数不同，例如C1中的属性被赋予2 分，C2中的属性被赋予1 分，未考虑的属性被赋予0 分.

定义3.用户群权重偏好次序.指针对查询用户群属性的有序集合GP={d1,d2,…,di},其中di代表任意属性，GP中属性对用户群的重要性程度呈非递增排列.用户群权重偏好次序综合考虑用户的偏好和权重.

定义4.K-准放松支配（KPRD）.设P为数据集，数据维度空间为D，dj为任意维度，总维度数为r，θ=（θ1,θ2,…,θK）是D上K个维度的无差异阈值.数据点pi，pt∈P，piK-准放松支配pt，记作piϾpt，当且仅当：其中1≤j≤K.

定义5.道路网多用户偏好Top-kSkyline 查询.给定道路网路段集R、查询用户群G、数据集P、用户的查询关键字集合keys和用户权重集合w，道路网多用户偏好Top-kSkyline 查询返回P的一个子集.该子集中数据点在道路网的距离维度和静态维度都不能被P中任意其他数据点支配，并且是根据用户群偏好和权重排序的Top-k个数据点.本文将道路网多用户偏好Top-kSkyline 查询方法记作MUP-TKS.

3 道路网多用户偏好Top-k Skyline 查询

本文提出的道路网多用户偏好Top-kSkyline 查询方法主要分为3 个部分：距离较优集选取﹑K-准放松支配和Top-k个数据点选取.

3.1 道路网距离较优集选取方法

定义6.Mindist 距离[24].r维欧氏空间中，点p到同一空间内某矩形N的最小距离为Mindist（N,p）.

定义7.Edist 距离.设查询用户群的最小外接矩形（minimum bounding rectangle，MBR）为Q，数据点p的MBR 为N，则min{Mindist（p,Q）}为（Q,N）最小欧氏距离，记作Edistmin；max{Mindist（p,Q）}为（Q,N）最大欧氏距离，记作Edistmax.

定义8.Ndist 距离.设查询用户群的MBR 为Q，数据点p的MBR 为N，有min{Ndist（p,Q）}为（Q,N）最小网络距离，记作Ndistmin；max{Ndist（p,Q）}为（Q,N）最大网络距离，记作Ndistmax，其中p为N中的任意数据点，Ndist（p,Q）为p到Q的网络距离.

定理1.设查询用户群的MBR 为Q，道路网中数据点构成的2 个中间节点分别为N1，N2，若DE1=Edistmin（Q,N2），DE2=Edistmax（Q,N1），DN1=Ndistmax（Q,N1），并且DE1＞DE2，DE1＞DN1，则N1►N2，且N2中任意数据点都被N1中数据点距离支配.

证明.假设DN2=Ndistmin（Q,N2），因为欧氏距离值一定小于等于道路网距离值，所以当DE1＞DE2且DE1＞DN1时一定有DN2≥DE1，可得DN2＞DN1，即N2中数据点到Q的最小网络距离大于N1中数据点到Q的最大网络距离，进而可得N2中任意数据点到Q的网络距离都大于N1中任意数据点到Q的网络距离.因此N1►N2，且N2中任意数据点被N1中任意数据点道路网距离支配.证毕.

剪枝规则1.设数据点构成的MBR 分别为N1，N2，查询用户群的MBR 为Q，如果满足：Edistmax（Q,N1）≤Edistmin（Q,N2），并且Ndistmax（Q,N1）＜Edistmin（Q,N2），则节点N2可被剪枝.

定义9.道路网最大距离的最小值.给定数据点p1，p2，查询用户群G，数据点p到查询点q的道路网距离为Ndist（p,q）.若有DN1=max{Ndist（p1,qi）}，DN2=max{Ndist（p2,qi）}（1≤i≤m），并且DN1＜DN2，则当前道路网最大距离的最小值为DN1，记作DN_MaxMin.对应的数据点为p1.

定理2.若节点N的Edistmin（Q,N）＞DN_MaxMin，则节点N可被剪枝.

证明.因为Edistmin（Q,N）＞max{Ndist（p,qi）}（1≤i≤m），所以Ndistmin（Q,N）＞max{Ndist（p,qi）}，即p►N，且N中数据点也被p距离支配.证毕.

剪枝规则2.若Edistmin（Q,N）≥DN_MaxMin，则节点N被支配，即N和N中数据点{p1,p2,···,pi}被剪枝.

如图1 所示，数据点p1，p2到查询用户群{q1,q2,q3}的最大网络距离分别为DN1，DN2，有DN1＞DN2，则DN_MaxMin=DN2.数据点{p3,p4,p5,p6,p7,p8}构成的MBR为N1；若Edistmin（Q,N1）＞DN_MaxMin，可得N1中数据点到各查询用户的网络距离大于DN_MaxMin，因为Edistmin（Q,N1）＞DN_MaxMin，且有min{Ndist（p2,qi）}≥Edistmin（Q,N1）（1≤i≤3），所以p2►N1，N1可被剪枝.

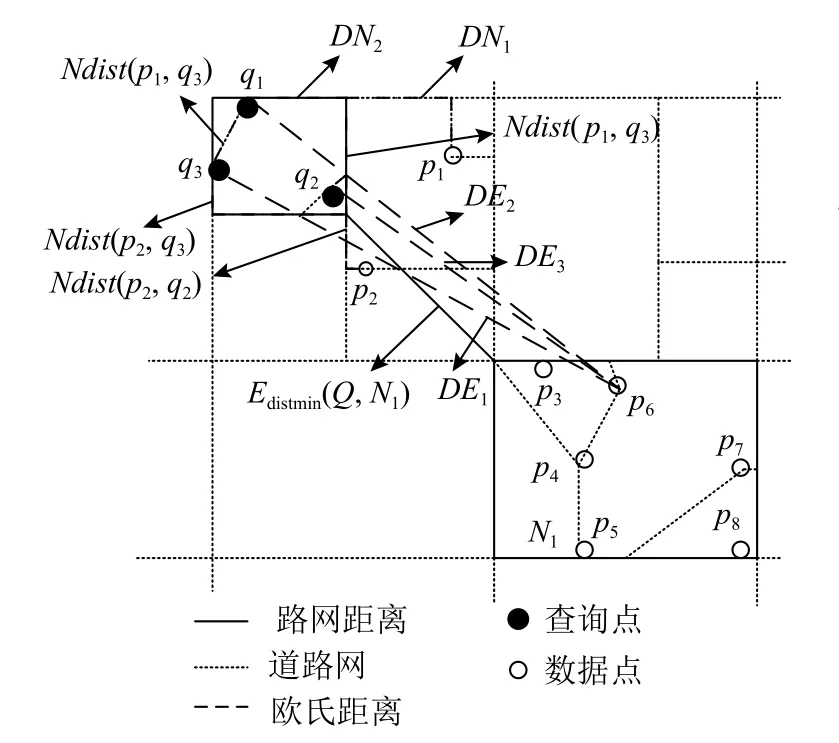
Fig.1 Example of pruning rule 2图1 剪枝规则2 示例

定理3.设DE为数据点pi到查询用户qj的欧氏距离，若min{DE（pi,qj）}＞DN_MaxMin（1≤j≤m），则pi被剪枝.

证明.假设p1为DN_MaxMin对应的数据点，若min{DE（pi,qj）}＞DN_MaxMin，则有Ndist（p,qj）＞DN_MaxMin（1≤j≤m），即数据点p1►p，p可被剪枝.证毕.

剪枝规则3.假设数据点p1为DN_MaxMin对应的数据点，若存在DN_MaxMin＜min{DE（pi,qj）}（1≤j≤m），则p1►pi，可将pi从候选集中删除，其中pi为任意不为p1的数据点.

为了减少计算，在剪枝前基于路网数据点的网络Voronoi 图构建Vor-R*-DHash 索引结构，如图2 所示.

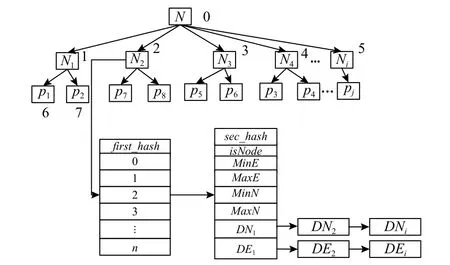
Fig.2 Index structure of Vor-R*-DHash图2 Vor-R*-DHash 索引结构

Vor-R*-DHash 索引结构构造过程有3 步：

1）构建路网所有数据点的网络Voronoi 图.

2）创建R*-tree.从R*-tree 的根部开始，从上至下、从左至右给每个节点编号，从0 开始编号.

3）构建2 级HashMap 结构，第1 级HashMap 为first_hash、key为R*-tree 中每个节点编号；第2 级HashMap为sec_hash、key为后续剪枝处理需要的值，包括isNode（非数据点的节点）、MinE（节点到Q的最小欧氏距离值）、MaxE（节点到Q的最大欧氏距离值 ）、MinN（节点到Q的最小网络距离值）、MaxN（节点到Q的最大网络距离值）、{DN1,DN2,…,DNi}（数据点到各查询用户的网络距离）、{DE1,DE2,…,DEi}（数据点到各查询用户的欧氏距离）.

2 级key对应的value值初始都为空，若数据点根据剪枝规则提前被剪枝，则这些值无需计算.DEi，DNi的值也是后续需要使用才被计算，并存入sec_hash.

基于剪枝规则1～3 和Vor-R*-DHash 索引结构，进一步给出距离较优集选取方法，如算法1 所示.

算法1.距离较优集选取方法 G_DBC.

输入：查询用户群G，道路网路段集R，数据集P；

输出：距离维度不被支配的距离较优集DBC.

算法1 首先构建Vor-R*-DHash 索引和查询用户群最小外接矩形Q，可快速得到距离查询点最近的数据点point，计算并保存sec_hash所需数据.将point加入距离较优集DBC，并初始化DN_MaxMin.接着将point父节点加入队列queue中，计算并保存sec_hash所需数据，并初始化N1.每次取出队头节点处理，依据剪枝规则1～3 进行节点的剪枝或者将节点加入DBC，并判断是否需要更新N1，DN_MaxMin等值，直至队列为空，循环结束.最后返回距离较优集DBC.

3.2 数据集的放松支配过程

3.2.1 获取用户群权重偏好次序

首先初始化整体属性权重集合.W={W1,W2,…,Wi}={0,0,…,0}；接着计算每个属性的整体属性权重值得到W；最后对整体属性权重值不为0 的属性降序排列，得到属性的重要性次序，即用户群权重偏好次序.

在获取用户群权重偏好次序时，为了减小计算开销，利用HMap1，HMap2分别保存优先考虑的属性和一般偏好的属性.当用户发起查询时，将C1中属性作为键，对应的用户权重作为值保存到HMap1；将C2中属性作为键，对应的用户权重作为值保存到HMap2.

进一步给出获取用户群权重偏好次序算法CDW，如算法2 所示.

算法2.获取用户群权重偏好次序算法 CDW.

输入：用户群G，用户查询关键字keys，用户权重w，维度空间D；

输出：用户群权重偏好次序GP.

① 初始化W为0；/*大小为数据集维度数*/

② 根据keys，w创建HMap1，HMap2；

③ fordj∈Ddo

④ 基于HMap1、HMap2和式（1）得到Wj；

⑤ end for

⑥ 根据W降序得到用户群权重偏好次序GP；

⑦ returnGP./*返回用户群权重偏好次序*/

3.2.2 基于用户群权重偏好次序的K-准放松支配

获取用户群偏好次序后，基于该次序进行放松支配处理.本文中K为整体属性权重值不为0 的维度数.放松支配过程的处理对象为DBC与静态Skyline集取并集后的集合S.经K-准放松支配后得到数量可控的候选结果集CS.

定理4.任意2 个数据点pi，pj∈P，若第i（i＞0）轮在K个维度上piϾpj，则数据点pi必定在前K-i维支配数据点pj.

证明.若在第i轮piϾpj，可知该轮的无差异阈值为（0,0,…,0,θK-i+1,…,θK），进而可得前K-i维使用的无差异阈值为（0,0,…,0），所以前K-i维为严格支配比较，即数据点pi必定在前K-i维支配数据点pj.证毕.

定理5.数据集P经过第i（i＞1）轮放松支配后所得结果集Si一定是第i-1 轮放松支配后所得结果集Si-1的子集.

证明.设第i轮放松的维度为第（K-i+1）～K维，第i-1 轮放松的维度为第（K-i+2）～K维，其余维度使用严格支配.可知第i轮的无差异阈值为（0,0,…,0,θK-i+1,θK-i+2,…,θK），第i-1 轮的无差异阈值为（0,0,…,0,θK-i+2,…,θK），进而可知第i-1 轮在前K-i+1 个维度为严格支配比较，即在前K-i+1 个维度的无差异阈值为（0,0,…,0）.第i轮不同于第i-1 轮之处在于对第K-i+1 维进行了放松支配，即在前K-i+1 个维度无差异阈值为（0,0,…,0,θK-i+1），所以有Si⊆Si-1.证毕.由定理4、定理5 可直接得出定理6.

定理6.给定数据集S，结果集数量随着每一轮放松而呈单调非递增趋势，即

为使返回的结果集更符合用户群偏好，并保证数量可控，基于定理4～6 进行逐次放松支配.逐次放松支配过程中，θ是D上K个维度的无差异阈值，θ=（θ1,θ2,…,θK）.假定当前放松轮次为第i轮（1≤i≤K），无差异阈值θ=（0,0,…,0,θK-i+1,…,θK）.位于di前面的维度重要性都要高于di，因此该轮放松支配维度d1～di-1都使用严格支配比较.放松支配从对用户群而言最不重要的属性开始，并预先将数据点按照用户群权重偏好次序非递增排序，距离维度值用数据点到查询用户群网络距离的最大值表示.

基于以上讨论，进一步给出基于用户群权重偏好次序的K-准放松支配算法KPRD，如算法3 所示.

算法3.基于用户群权重偏好次序的K-准放松支配算法KPRD.

输入：用户群G，无差异阈值θ，并集S，数据维度空间D，k值，用户查询关键字keys，用户权重w；

输出：候选结果集CS.

3.3 Top-k 个数据点选取方法

通过放松支配处理后可有效控制返回用户群的结果集大小，本节进一步给出Top-k个数据点选取策略，使返回结果集有序.利用z-整体属性权重值的打分函数选取Top-k个数据点，处理对象为候选结果集CS.

定义10.单调打分函数F[25].数据集中数据点作为输入域将数据点映射到实数范围.F由r个单调函数构成，F={f1,f2,…,fr}.对于数据集中任意数据点，有，其中fj（p[dj]）为数据点在dj维度的单调函数.

定理7.假设数据集P的单调打分函数为F，若数据集中任意一个元组有最高的分数，那么它一定是Skyline 点.

证明.以反证法进行证明.假设有p1，p2∈P，p1的得分F（p1）为数据集的最高得分，F（p1）＞F（p2），p1不是Skyline 点，p2支配p1，p1[dj]≤p2[dj]（1≤j≤r），则可得，即F（p1）≤F（p2），与假设矛盾.证毕.

定理8.数据集P根据任意单调打分函数所得数据点顺序是Skyline 支配的拓扑顺序.

证明.以反证法进行证明.假设存在2 个数据点p1，p2∈P，单调打分函数为F，p1支配p2，F（p1）＜F（p2），根据定理7 可知，p1支配p2，则有F（p1）≥F（p2）,与假设矛盾.所以如果F（p2）＞F（p1），可能有p2支配p1，但可以确定p1不可能支配p2.如果F（p1）=F（p2），则p1支配p2或p2支配p1（这两者是等价的，会根据属性的映射关系排序），或者p1和p2之间不具备支配关系.因此依据打分函数F所得数据点顺序是按照Skyline支配关系的一个拓扑顺序.证毕.

定义11.线性打分函数[25].给定线性打分函数L，一般化形式为，其中ωj为实常数，p[dj]为数据点在dj维度的取值.

定义12.z-整体属性权重值.给定数据集P，数据点pi∈P，pi在dj维度的z-整体属性权重值为

定理9.数据点任意维度的fj（p[dj]）是单调的.

证明.因为ωj=Wjζj，在打分阶段Wj为实常数，所以可得ωj为实常数，且随着数据点维度值变大，它的z值也变大，因此数据点的任意维度fj（p[dj]）是单调的.证毕.

定义13.基于z-整体属性权重值的打分函数.数据点pi各维度z-整体属性值之和为它的得分，记作F（pi）:

定理10.F（pi）是单调打分函数.

证明.因为有F(pi)=fj(p[dj])，根据定理9 可知数据点的任意维度fj（p[dj]）随着维度值变大单调递增，它们具备相同的单调性，因此F（pi）也是单调的.证毕.

进一步给出Top-k个数据点选取方法，如算法4所示.

算法4.Top-k个数据点选取方法TK_DC.

输入：候选结果集CS，整体属性权重集合W，维度优劣集合ζ；

输出：Top-kSkyline 结果集.

① forpi∈CSdo

② 计算数据点的z-整体属性权重值；/*根据式（4）*/

③ 计算数据点得分；/*根据式（5）*/

④ end for

⑤ 根据F（pi）降序排序；

⑥ return Top-k个数据点.

算法4 主要对经过算法3 处理后的候选结果集CS打分，并对行②③计算CS中各个数据点的得分，基于行⑤⑥数据点的得分排序，输出Top-kSkyline 结果集给用户群.

综合距离较优集选取﹑K-准放松支配和Top-k个数据点选取的处理过程，进一步给出算法5 MUPTKS 的算法.

算法5.道路网多用户偏好Top-kSkyline 查询算法MUP-TKS.

输入：数据集P，道路网路段集R，用户群G，用户查询关键字keys，用户权重w，无差异阈值θ，k，维度优劣集合ζ；

输出：Top-kSkyline 结果集.

① 预先计算保存数据集的静态Skyline 集；

② 距离较优集选取方法G_DBC；/*调用算法1*/

③ 对距离较优集与静态Skyline 集求并集S；

④K-准放松支配算法KPRD；/*调用算法 3*/

⑤ Top-k个数据点选取方法TK_DC./*调用算法4*/

4 实验比较与分析

本节主要对MUP-TKS 进行实验以及性能评估.实验对比算法为道路网单用户偏好Skyline 算法UPBPA[26]、K支配空间偏好Skyline 算法KSJQ[23]以及基于时间道路网多用户偏好Skyline 算法DSAS[27].UPBPA 算法适用于道路网单用户，为了更好地与本文所提MUP-TKS 进行对比，将其扩展，对查询用户群的每个用户分别运行该算法；再对子结果集取并集，得到候选结果集CS；最后对候选结果集基于z-值的打分函数打分，得到Top-k个数据点，扩展后的算法称为EUP-BPA.将KSJQ 算法扩展，对每个用户单独执行该算法，用户偏好对应它的K个子空间；对每个用户的结果集取并集后得到候选结果集；对候选结果集CS基于z-值的打分函数打分，得到Top-k个Skyline结果集，扩展后的算法称为EKSJQ.将DSAS 算法扩展，对满足不同用户需求的数据点基于z-值打分函数打分，按照数据点得分从高至低返回Top-k个Skyline结果集，扩展后的算法称为EDSAS.

4.1 数据集及实验环境设置

实验使用真实道路网数据集.道路网数据集①http://www.cs.utah.edu/～lifeifei/SpatialDataset.htm是北美2.5×107km2范围内的路段信息，它包含175 813个节点和179 179 条边.兴趣点数据集②https://www.ahla.com/来自北美酒店及登记信息.查询用户采用随机生成的方式.本文使用Vor-R*-DHash 索引结构组织数据集.实验参数取值范围如表1 所示，每个用户最大关注维度为4.每个实验采取单一变量原则，其余变量为默认值，实验结果取30 次实验运行的平均值.

Table 1 Experimental Parameter Setting表1 实验参数设置

实验环境为：Windows 10（64b），CoreTMi6-5200U CPU @2.20 GHz 2.19 GHz 处理器，12 GB 运行内存.在IntelliJ IDEA 开发平台上使用Java 实现本文所提的算法MUP-TKS 和对比算法EUP-BPA，EKSJQ，EDSAS.

4.2 算法对比实验

1）用户数量对算法性能的影响

为了分析用户数量对算法性能的影响，本实验对不同用户数量下的MUP-TKS，EKSJQ，EDSAS，EUPBPA 算法进行测试，观察算法在不同用户数量下的CPU 运行时间、候选结果集CS数量的变化情况.

图3 展示了4 种算法在不同用户数量下CPU 运行时间变化情况.由图3 可知，随着用户数量的增加，4 种算法的CPU运行时间都在增加.因为用户数量增加导致不同用户的偏好情况增加，从而需要更多时间处理用户偏好.MUP-TKS 的CPU 运行时间增长趋势没有其他3 种算法的增长趋势大，主要原因是MUP-TKS 将多用户的偏好转换成用户群权重偏好次序，对数据集按照该次序预排序，再进行K-准放松支配，使用户数量增加对CPU 运行时间的影响减小.

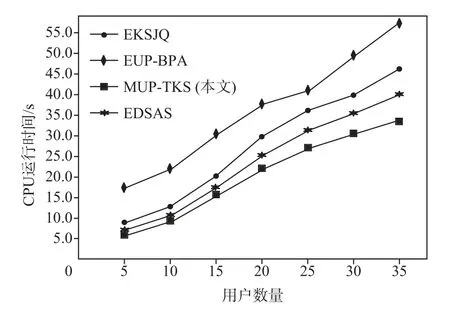
Fig.3 Effect of user number on CPU execution time图3 用户数量对CPU 运行时间的影响

图4 展示了4 种算法随着用户数量的变化，候选结果集CS数量的变化情况.由图4 可知随着用户数量的增加，CS的数量变大.但MUP-TKS，EKSJQ，EDSAS 算法的变化趋势远没有EUP-BPA 算法的变化趋势大，主要因为EUP-BPA 算法需要对每个用户进行偏好Skyline 查询，再合并各用户的偏好Skyline结果集.

Fig.4 Effect of user number on CS number图4 用户数量对CS 数量的影响

2）数据规模对算法性能的影响

为了分析数据规模对MUP-TKS 性能的影响，本实验对不同数据规模下的MUP-TKS，EKSJQ，EDSAS，EUP-BPA 算法进行测试，观察4 种算法在不同数据规模下CPU 运行时间、CS数量的对比情况.

由图5 可知，随着数据集规模变大，CPU 运行时间不断增加，因为当数据集规模变大时，需要比较的元组数量增加.而MUP-TKS 的增长趋势比其他3 种算法小，主要因为MUP-TKS 利用剪枝策略和Vor-R*-DHash索引提前剪枝大量不可能成为Skyline 的数据点，减少了元组比较次数.

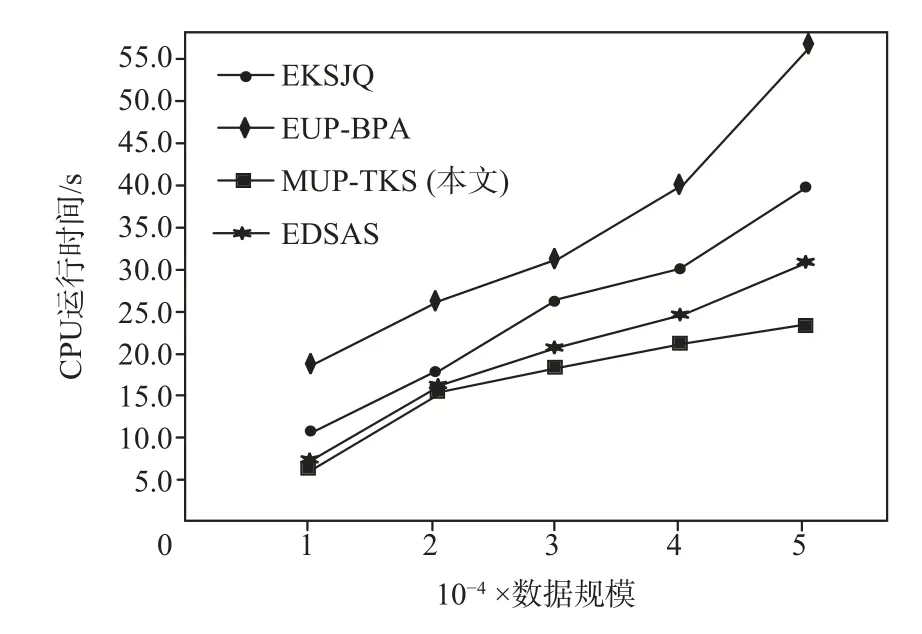
Fig.5 Effect of data size on CPU execution time图5 数据规模对CPU 运行时间的影响

3）k值对算法性能的影响

图6 展示了4 种算法随着k值变化CPU 运行时间变化的情况.随着k值变化，MUP-TKS 的CPU 运行时间没有太大变化，因为MUP-TKS 在每一轮放松支配后会保存结果集，当k值变化时，可直接找到对应符合大小要求轮次的CS打分，即可得到Top-kSkyline结果集，该过程时间消耗很小.而EKSJQ，EUP-BPA算法都需要重新计算，时间消耗较大.

Fig.6 Effect of k value on CPU execution time图6 k 值对CPU 运行时间的影响

图7 展示了4 种算法随着k值变化元组比较次数的变化情况.可以发现MUP-TKS 随着k值增大，元组比较次数减少，因为当k值增大时，放松支配的轮次减少.而随着k值增大，EKSJQ，EUP-BPA 算法的元组比较次数增多，因为需要进行更多的支配比较找到Topk个数据点.随着k值增大，EDSAS 算法的元组比较次数基本没有变化.

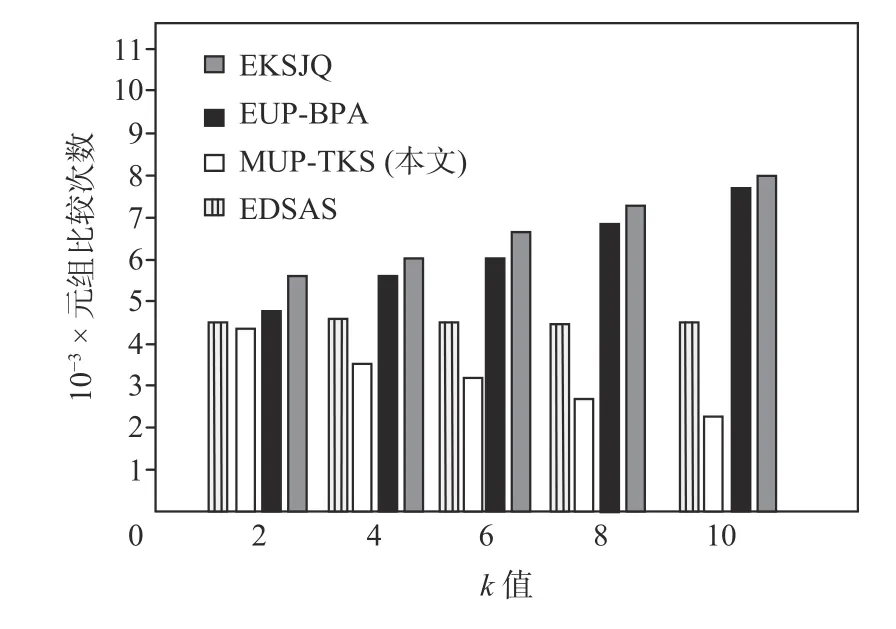
Fig.7 Effect of k value on the number of tuple comparison图7 k 值对元组比较次数的影响

4）无差异阈值对算法性能的影响

本实验分析无差异阈值对MUP-TKS 性能的影响.图8 展示了MUP-TKS 在不同无差异阈值下CPU运行时间的变化情况.由图8 可知，若只考虑第1 轮放松时间，无差异阈值变化对第1 轮放松的CPU 响应时间影响不大，因为不同无差异阈值的初始数据集大小都是相同的，处理相同数据集规模的时间差异不大.而算法总运行时间随着阈值增大而减小，因为无差异阈值增大后，放松支配时会删减更多被支配的元组.

Fig.8 Effect of θ on CPU execution time图8 θ 对CPU 运行时间的影响

5 总结

本文针对现实生活中道路网多用户场景的偏好Top-kSkyline 查询问题，进行深入分析与研究.作为道路网上单用户偏好Skyline 查询问题的补充，提出了一种基于道路网环境下多用户偏好Top-kSkyline查询方法.该方法利用剪枝规则和索引减少了距离计算开销，并利用用户群权重偏好次序进行放松支配，使结果集可控.实验结果表明，本文方法能有效解决道路网多用户偏好查询问题，返回的结果集可以满足多用户偏好与权重需求，可以提供有效参考价值.下一步研究重点主要集中在对多查询用户移动情况下偏好 Top-kSkyline 查询问题的处理.

作者贡献声明：李松提出了方法思路和技术方案；宾婷亮和郝晓红负责算法优化、完成部分实验并撰写论文；张丽平完成部分实验；郝忠孝提出指导意见并修改论文.