时态图顶点介数中心度计算方法

张天明 赵 杰 金 露 陈 璐 曹 斌 范 菁

1（浙江工业大学计算机科学与技术学院 杭州 310023）

2（浙江大学计算机科学与技术学院 杭州 310013）

介数中心度（betweenness centrality,BC）通过计算经过顶点的最短路径数来确定顶点在图结构中的重要程度，是图顶点重要性计算的一种流行方式，最早由Freeman[1]提出.顶点的介数中心度越大，则顶点对图中其他顶点的控制能力越强，介数中心度算法被广泛应用于社会网络分析[2-3]、蛋白质交互网络影响预测[4]、社区发现[5]等.

现有的介数中心度算法主要聚焦于普通图，然而现实场景中建模的图常为时态图，边上带有时态信息.例如电子邮件网络[6]边上附带有邮件发送/接收时间；社交网络[7]边上附带有人与人的接触时间.图1 是一个电子邮件网络示例，顶点表示用户，边表示用户之间发送/接收邮件的关系，边上时间戳表示邮件发送/接收或转发/接收的时间.具体地，用户1在3 个不同时间点向用户2 共发送了3 份邮件，而后用户2 将邮件1 和邮件2 转发给用户3 和用户4，并将邮件3 转发给用户5.电子邮件网络上介数中心度计算有助于精确推断网络结构[8]、用户活跃程度等.图2是一个农贸市场接触网络示例，顶点表示供货商、商户、消费者；边表示他们之间的接触时刻.具体地，消费者1 和消费者2 在商户1 消费；消费者3 在商户1和商户2 消费.蔬菜供货商为商户1 送货，水果供货商为商户1 和商户2 送货.在传染病疫情暴发时，接触网络上介数中心度计算有助于识别超级传播者[9]，控制传染病的传播.

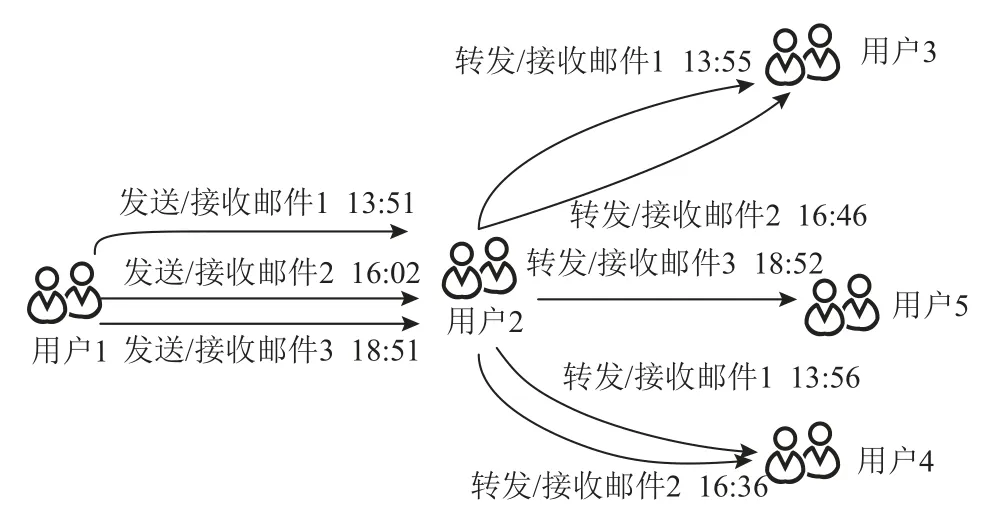
Fig.1 An example of email network图1 电子邮件网络示例

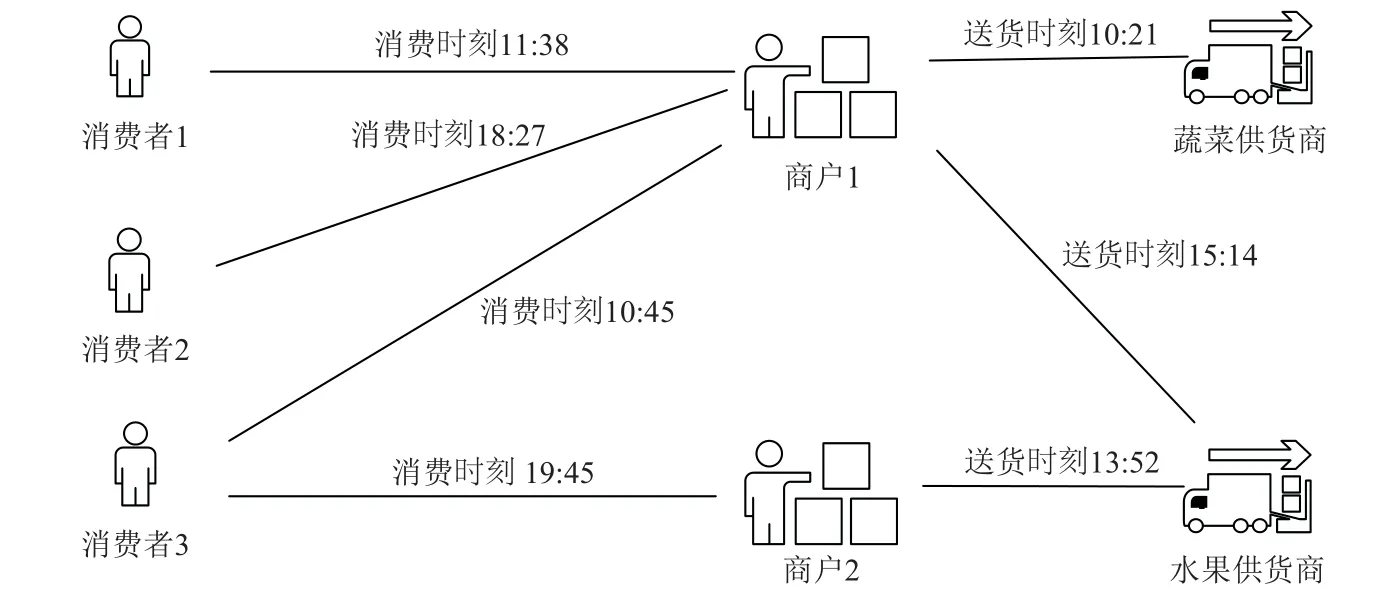
Fig.2 An example of agricultural market contact network图2 农贸市场接触网络示例

普通图上介数中心度计算忽略了重要的时态信息，而时态信息对于信息流传播扩散[10]具有重要作用.鉴于此，本文研究的时态图顶点介数中心度计算方法与已有的普通图介数中心度计算方法相比，时态图包含时态信息，且1 对顶点之间存在多条被不同时间戳标记的边，因此时态图上介数中心度计算难度更大.具体原因可分为2 方面：

1）时态图顶点介数中心度需要根据时态最短路径计算，而时态最短路径的定义方法多样，且计算时需要考虑时态边之间的时序依赖关系.例如图3（a）给出的时态图示例中，边上的值为时间戳信息.如果不考虑时态信息，则a到d的最短路径为a→c→d，但实际上a经c到d是不可达的，因为a到c的时间为4（＞3）.所以计算时态最短路径时需要考虑时态边与边之间的时序依赖关系，记a到d的时态最短路径为a→b→c→d.

Fig.3 Examples of temporal graph and general graph图3 时态图和普通图示例

2）针对时态图，普通图上介数中心度的计算理论与方法已不再适用，需要设计全新的理论与方法.这是因为普通图中的介数中心度计算方法主要根据Brandes 算法[11]设计，Brandes 算法有效的关键理论是最短路径的子路径依然是最短路径，即最优子结构特性.然而时态最短路径并不满足此特性.例如图3（b）给出的普通图中，a→c→d是1 条最短路径，则子路径a→c一定是最短路径.而在时态图中（如图3（a）所示），时态最短路径a→b→c→d的子路径a→b→c很明显不是时态最短路径，a到c的时态最短路径为a→c.

为了解决这2 个难点，本文根据时态边之间的时序依赖关系，定义了严格（时态递增）和非严格（时态非递减）2 种时态路径类型，提出了基于消息传播的2 阶段迭代计算框架以高效计算时态图顶点介数中心度.其中，第1 阶段采用自顶向下的广度优先遍历方式计算时态最短路径；第2 阶段采用自底向上的方式计算顶点的后继节点和孩子节点对其介数中心度的贡献值，并设计了基于消息传播机制的迭代累积计算方法.为了提高效率和可扩展性，实现了基于OpenMP（open multiprocessing）框架的多线程并发算法FTBC（fast temporal betweenness centrality）.概括而言，本文的主要贡献有3 点：

1）提出了自顶向下和自底向上结合的2 阶段计算框架，并设计了基于消息传播机制的迭代累积计算方法以高效计算时态图顶点介数中心度.

2）提出了基于OpenMP 框架的多线程并发算法FTBC，以提高时态图顶点介数中心度计算的效率和可扩展性，并理论分析了算法的复杂度.

3）基于8 个真实的时态图数据集进行了大量的实验评估，验证了多线程FTBC 算法相比目前流行的方法计算性能更优，可扩展性更强.

1 相关工作

本节分别概述已有的普通图和时态图介数中心度计算方法.

1.1 普通图介数中心度计算方法

针对普通图，Brandes[11]推导了经典的成对依赖、迭代计算理论，并基于此提出了精确介数中心度计算方法.算法空间复杂度为O(n+m)，时间复杂度为O(nm)（无权图）或O（nm+n2log2n）（有权图），其中n和m分别表示顶点数和边数.Erdős 等人[12]提出了Brandes++算法，该算法采用分治策略，利用图基础结构加速计算.Sariyüce 等人[13]提出了BADIOS 算法，该算法针对无向无环图，先将一些特殊顶点压缩，并利用顶点、桥边将图划分为多个子图，而后在子图上计算顶点的介数中心度.Baglioni 等人[14]提出利用图的拓扑特征加速计算.但文献[12-14]所提算法的最坏时间复杂度仍与Brandes 算法[11]相同.

为了提高介数中心度计算效率，研究人员提出了近似算法.为了避免计算所有顶点对之间的最短路径，近似算法的总体思想是基于采样方法计算部分顶点之间的最短路径，并基于此估算所有顶点的介数中心度.为了保证结果质量，近似算法通常理论推导采样数或迭代更新介数中心度值，直到满足预置的终止条件.Brandes 等人[15]提出了基于顶点采样的方法，其利用霍夫丁不等式[16]估计误差概率.Riondato 等人[17]提出了基于最短路径采样的方法RK，其利用顶点直径（vertex diameter,VD）和VC（vapnikchervonenkis）维[18]估算达到要求精度所需的最少样本数.RK 首先采样一对顶点，然后再基于采样顶点对的一条最短路径而不是所有最短路径来近似计算顶点的介数中心度.此外，由于计算精确的顶点直径需要所有顶点对之间的最短路径，此操作非常耗时，因此RK 随机采样一个顶点，并根据该顶点到图中其他顶点的单源最短路径距离估计顶点直径.基于RK，Borassi 等人[19]提出了KADABRA 算法，其采用双向广度优先搜索方式来减少最短路径的采样时间，在介数中心度估计时允许为每个顶点设置不同的概率置信度.Riondato 等人[20]提出了ABRA 算法，其利用渐进式随机抽样，基于拉德马赫平均值和伪维估计采样数.Cousins 等人[21]提出了Bavarain 算法，其采用蒙特卡洛经验拉德马赫平均值[22]估计更加严格的样本数上界，进而保证结果精度.Pellegrina 等人[23]提出了SILVAN 算法，与Bavarain 算法相同的是，SILVAN同样采用蒙特卡洛经验拉德马赫平均值估计样本数上界；与Bavarain 不同的是，Bavarain 仅适用于均匀边界，而SILVAN 可以用于均匀和非均匀边界.

然而，无论是普通图介数中心度精确计算方法还是近似计算方法，方法有效的关键理论是最优子结构性质，而时态图不满足最优子结构特性，因此无法直接扩展到时态图.

1.2 时态图介数中心度计算方法

一些工作将时态图看作是一系列图的镜像，即动态图，而后研究动态图介数中心度计算.Lee 等人[24]将动态图分解为连通分量后再进行BC 值更新计算以减少搜索空间.Green 等人[25]提出最短路径树结构加速动态图BC 值的更新.Kourtellis 等人[26]将最短路径树结构压缩存储以减少内存占用.Kas 等人[27]拓展了动态APSP（all pairs of shortest path）算法[28]以实现BC 值动态更新.Bergamini 等人[29]提出了半动态的近似计算方法以支持顶点和边的插入操作.Hayashi 等人[30]提出了全动态的近似算法以支持边和顶点的插入和删除.然而文献[25-30]算法均将时态图视为图镜像集合，没有考虑时态边之间的时序依赖关系，本质上还是基于普通图的最优子结构性质设计的方法.

与本文研究问题最相似的工作为Buß等人[31]提出的时态图顶点介数中心度精确计算算法，其首先构建顶点的前置图，使得前置图上满足最优子结构性质，而后将Brandes 算法理论扩展，运用在前置图上进行计算.另一篇较相似的工作为Tsalouchidou 等人[32]提出的算法，其将路径长度与持续时间结合起来作为时态最短路径定义标准，并在时态图定长静态窗口上计算介数中心度精确值.本文实验测试了Buß等人[31]提出的算法，发现当时态图边数为3 万时，其在内存16GB 的机器上已无法运行.Tsalouchidou 等人[32]提出的算法对于时间离散程度较大的时态图而言，需要设置较大的静态窗口值，导致复制静态窗口时耗费了大量的时间.可见，文献[31-32]工作存在计算效率较低、可扩展性差的问题.

2 问题定义

本节主要介绍时态图、时态路径、时态最短路径、时态介数中心度的相关概念，并给出问题定义.

定义1.时态图.本文定义的时态图既可以是有向的，又可以是无向的，表示为G=(V,E,T).其中，V表示顶点集合；E表示时态边集合；T为时间戳集合.时态图中2 点之间可以有多条时态边.具体地，时态边ei=（ui,vi,,ti）表示顶点ui与vi之间的事件发生时间为ti，ti∈T.

定义2.严格与非严格时态路径.从顶点u到vk的时态路径表示为其中，p的第1 条边e1=（u,v1,t1），第i条边ei=（vi-1,vi,ti）（1 ＜i＜k），第k条边ek=（vk-1,vk,tk）使得对于任意的1 ≤i＜k，ti≤ti+1.特别地，当k=1，p也是1 条时态路径.进一步地，如果对于任意的1 ≤i＜k，ti＜ti+1，则p称为严格时态路径；否则p称为非严格时态路径.令|p|=k表示时态路径的长度.

定义3.时态最短路径.给定从顶点u到v的时态路径ps，如果不存在从u到v的其他时态路径p满足路径长度|p|＜|ps|，则ps是时态最短路径.特别地，当|ps|=1 时，ps也是一条时态最短路径.

定义4.时态介数中心度.给定时态图G=(V,E,T)，令σsf表示顶点s到顶点f的时态最短路径数目；σsf（v）表示由顶点s经顶点v到顶点f的时态最短路径数目，则对于所有顶点v∈V，v的时态介数中心度TBC（v）定义为TBC（v）=.

3 算法介绍

本节详细阐述基于消息传播的2 阶段迭代计算框架以及基于OpenMP 框架的多线程并发算法FTBC.

3.1 2 阶段迭代计算框架

为了清晰地说明框架的整体思路和2 阶段计算过程，首先定义了分裂点集合.

定义5.分裂点集合.给定时态图G=(V,E,T)，对于任意的顶点v∈V，v的分裂点集合表示为S（v）={（v,tm）|1≤m≤h}，其中tm是v入边中到达v的时间实例，h表示不同的到达时间实例数.

图4（a）给出了一个时态图G示例.G由6 个顶点和15 条时态边组成.以顶点b为例：b的分裂点集合S(b)={(b,0),(b,2),(b,4)}.

2 阶段迭代计算框架中，第1 阶段采用自顶向下的广度优先遍历方式计算时态最短路径.具体地，将每个顶点u作为源点，自顶向下计算源点u到其他顶点和分裂点的最短路径数.这个阶段需要保存的主要数据结构为：

1）σuv和σu（v,t）分别记录源点u到v和源点u到分裂点(v,t)的时态最短路径数.

2）Duv和Du（v,t）分别记录源点u到v和源点u到分裂点（v,t）的时态最短路径长度.

3）flag（v,t）标记（v,t）是否是源点u到v的时态最短路径的终点，如flag（v,t）=1，则表示（v,t）是源点u到v的时态最短路径的终点；否则flag（v,t）=0.

4）P（v,t）记录（v,t）的前驱分裂点集合.对于时态最短路径而言，（u,tk）为（v,tk+1）的一个前驱分裂点.

第2 阶段基于消息传播的机制，采用自底向上的方式迭代计算每个顶点的所有分裂点的时态介数中心度.这个阶段需要保存的主要数据结构为：

TBC（v）和δu（v,t）分别记录v的时态介数中心度和源点u经过分裂点（v,t）的时态最短路径中，（v,t）的所有后续节点对（v,t）的贡献值大小，其中δu(v,t)=

由于时态最短路径不满足子结构特性，因此需要分别计算分裂点的后继节点和孩子节点对其时态介数中心度的贡献值.具体地，对于时态最短路径而言，（v,tk+1）称为分裂点（u,tk）的孩子节点；（w,tk+2）…（z,tn）称为（u,tk）的后继节点.则对于分裂点（u,tk），需要计算2 部分贡献值：第1 部分为其后继节点（w,tk+2）…（z,tn）对其时态介数中心度的贡献值，需要迭代计算得到；第2 部分为其孩子节点（v,tk+1）对其时态介数中心度的贡献值.2部分贡献值均通过消息传播给分裂点（u,tk）.以图4（a）为例：当根据时态最短路径更新分裂点（b,0）的时态介数中心度时，需要考虑其孩子节点（c,1）和其后继节点（e,2）的贡献值.由于flag（c,1）=0，即（c,1）不是a到c的时态最短路径的终点，因此（c,1）对（b,0）的贡献值为0；只需计算第1 部分贡献值，即后继节点（e,2）对（b,0）的贡献值.

3.2 FTBC 算法

基于2 阶段迭代计算框架，本节提出了算法1.

算法1.时态图介数中心度计算算法FTBC.

输入：时态图G=(V,E,T)，线程数#threadnum；

输出：所有顶点的介数中心度{TBC(u),u∈V}.

FTBC 算法的输入为时态图G和自定义的线程数，输出为G中所有顶点的时态介数中心度.首先，FTBC 创建线程，初始化TBC数组（行①）.然后，对于时态图中的每一个顶点u，FTBC 委派空闲线程执行Compute方法计算顶点的TBC值（行②～④）.最后，如果所有线程终止，FTBC 返回所有顶点的TBC值（行⑤～⑦）.

Compute方法是一个2 阶段迭代计算的过程.阶段1 通过广度优先搜索的方式遍历时态图以完成距离、前驱分裂点和最短路径数的计算，并确定分裂点的flag值（行⑧～⑬）.具体地，Compute首先初始化栈S（行⑧）.然后从当前源点u出发遍历严格或非严格时态路径，将首次遍历到的分裂点（w,t′）加入S中，并计算源点u到分裂点（w,t′）的最短路径数σu（w,t'）、源点u到分裂点（w,t′）的距离Du（w,t'）、源点u到顶点w的最短路径数σuw、源点u到w的距离Duw以及分裂点（w,t′）的前驱分裂点集合P（w,t′）（行⑨～⑩）.如果分裂点（w,t′）确定是u到w的时态最短路径的终点，则令flag（w,t′）=1（行⑪～⑬）.阶段2 根据引理1自底向上迭代计算分裂点的时态介数中心度，进而累加得到最终顶点的时态介数中心度（行⑭～㉖）.具体地，当栈S不为空时，从S中弹出分裂点（w,t′），如果flag（w,t′）=1，则计算（w,t′）对其前驱分裂点（v,t）的贡献值（行⑭～⑲）；接着，累加计算（v,t）经（w,t′）到达的所有后继节点对（v,t）的贡献值（行⑳～㉒）.迭代计算这2 部分贡献值直至S为空.最后，Compute累加计算顶点的时态介数中心度（行㉔～㉖）.

4 实验分析

本节在真实的数据集中对FTBC 算法进行实验测试，并与2 种流行算法进行对比，以验证FTBC 的效率.

4.1 实验环境和数据集介绍

本文采用了8 个真实的数据集进行实验测试.email[8]数据集是一家中型制造企业员工之间的内部电子邮件通信网络，hypertext[33]是参会者面对面的接触网络；以hs 为前缀的3 个数据集[34-36]是由高中生与朋友构成的联络网络；hospital[37]，school[36]，infectious[33]分别为患者和护工、老师和学生、参展人之间构成的接触网络.其中email 数据集来自KONECT[38]，其他7 个数据集均来自ScocialPattern[39].表1 给出了数据集的统计信息，其中|V|表示顶点数，|E|表示边数，|D|表示时态区间.时态区间为整个时态图中最大时间戳和最小时间戳的差值.

Table 1 Dataset Information表1 数据集信息

本文将FTBC 与2 个流行算法SBT 算法[31]和SWTBC 算法[32]进行对比.相关实验代码分别从文献[40-41]中获取.在实验测试过程中，为取得较好的计算性能，除infectious 外的所有数据集默认线程数均设置为8，infectious 数据集由于内存限制，线程数设置为1.本文所有实验程序均使用C++语言编写，实验测试环境为一台配置为英特尔至强CPU 处理器E5-2640 v4 2.40 GHz，128 GB 内存，Linux 系统版本为CentOS 7.9 的服务器.

4.2 实验结果分析

4.2.1 时态介数中心度分布实验

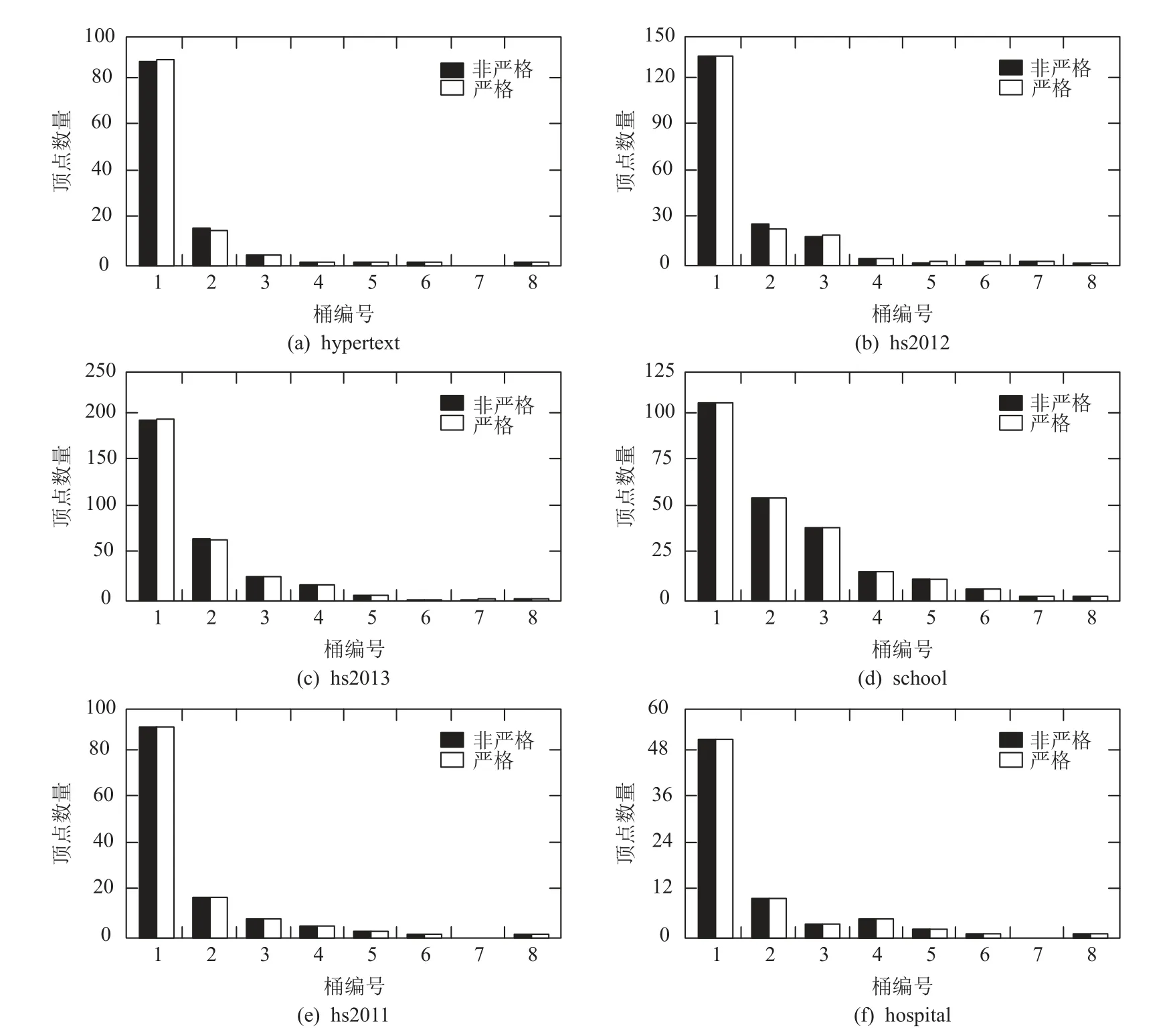
Fig.5 TBC distribution of different datasets图5 不同数据集的顶点介数中心度分布

4.2.2 时间效率对比实验

表2 给出了FTBC，SBT，SWTBC 算法的时态介数中心度计算时间.其中，FTBC 和SBT 算法名称前加上前缀“N”为基于非严格时态路径计算的时态介数中心度，加上前缀“S”为基于严格时态路径计算的时态介数中心度.SWTBC 算法仅支持非严格的时态路径.首先可以看出无论基于严格的还是非严格的时态最短路径计算方式，FTBC 算法的计算效率最高.具体地，FTBC 计算时间比SBT 快0.7～3 倍，比SWTBC 算法最多快4 个数量级.这是因为，FTBC 算法采用2 阶段迭代计算框架，基于引理1，运用并发机制高效迭代计算介数中心度.SBT 算法为了降低内存使用，需要不断花费时间清空数据结构中的值；SWTBC 算法由于数据集中时间离散程度大，需要设置静态窗口值较大，在复制静态窗口中的图数据方面花费了大量的时间，导致其效率最低.

Table 2 TBC Computation Time表2 顶点介数中心度计算时间 s

4.2.3 线程数对效率的影响实验

实验验证了线程数对时态介数中心度计算时间的影响.图6 给出了6 个数据集分别在线程数为1，8，16，24，32，40 进行实验的结果.从图6 可以看出时态介数中心度的计算时间随着线程数的增加呈先减后增的趋势.这是因为随着线程数的增加，顶点并发计算数增多，计算效率提高.但当线程数增加到一定数量后，线程开销主导了整体计算开销，线程切换和保证数据一致性的开销增大导致计算效率降低.

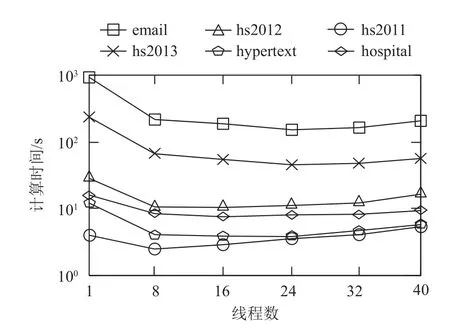
Fig.6 Effect of the number of threads on different datasets图6 线程数对不同数据集的影响

5 总结

本文研究了时态图上精确介数中心度计算问题，设计了一种高效的基于消息传播的2 阶段迭代计算框架，提出了基于OpenMP 框架的多线程并发算法FTBC，通过引理1 理论证明了自底向上传播机制的正确性，并通过示例解释了FTBC 算法的2 阶段迭代计算过程.基于8 个真实的时态图数据集，与2 种流行方法进行了时间效率对比，实验验证了FTBC 算法的高效性与可扩展性.通过理论与实验分析可以看出，精确计算时态介数中心度复杂性较高，设计高效的近似时态介数中心度算法是一个重要且值得研究的问题，后续工作计划对其展开深入研究.

作者贡献声明：张天明负责问题定义、方法设计、数据分析与论文撰写和修改工作；赵杰负责方法实现、实验验证、实验结果可视化；金露负责数据收集、实验测试和实验整理；陈璐负责实验分析与结果验证、论文写作指导；曹斌指导论文写作并提出修改建议；范菁指导论文写作并提出修改建议.