基于身份的群组密钥分发方案

王后珍 秦婉颖 刘 芹,3 余纯武 沈志东

1（武汉大学国家网络安全学院 武汉 430072）

2（先进密码技术与系统安全四川省重点实验室（成都信息工程大学） 成都 610054）

3（空天信息安全与可信计算教育部重点实验室（武汉大学） 武汉 430072）

4（武汉大学计算机学院 武汉 430072）

随着互联网技术的迅速发展和社交软件的大量涌现，人们越来越依赖于即时通讯软件进行网络在线交流.现代的即时通讯软件不仅能提供私聊功能，还能够提供群聊功能.无论是在工作场所还是学术领域，群聊在促进高效合作、提供知识交流平台和增进人际互动等方面都发挥着积极作用.

网络群聊为人们的生活带来了便利的同时也带来了一些安全问题.由于群聊中产生的消息在不安全的公开信道上传输，攻击者可以通过窃听信道来获取某个用户在群聊中发送和接收的消息，从而导致用户隐私数据的泄露，给用户造成损失.因此，为了保障群聊中发送和接收消息的安全性，需要采取有效措施.针对这一问题，常用的解决方法是在传输之前对群聊中传递的消息进行加密，然而，需要解决的问题是如何让参与群聊的用户具有一个相同的共享会话密钥.

1976 年，Diffie 等人[1]提出了Diffie-Hellman 密钥交换协议，用于在一对一通信中建立共享会话密钥.然而，Diffie-Hellman 密钥交换协议只能用于在2 个用户之间建立共享密钥，并不适用于群组密钥的建立[2].

为了解决在多用户场景下建立群组密钥的问题，许多方案应运而生.建立群组密钥的方案总体上可分为2 类，分别是群组密钥协商方案和群组密钥分发方案[3-5].

群组密钥协商是由所有参与群组通信的用户一起合作共建群组密钥，不依赖于可信的中央权威机构，群组密钥直接由群组内成员共同决定[6].根据群组密钥类型的不同，这类方案分为对称群组密钥协商和非对称群组密钥协商[7-8].在对称群组密钥协商方面，自Ingemarsson 等人[9]提出通过扩展Diffie-Hellman密钥交换协议来为n个参与者提供对称群组密钥的方案以来，许多学者对此进行了深入研究，并提出了构造各异的对称群组密钥协商方案.Naresh 等人[10]提出了一种基于集群的混合分层组密钥协商框架，为大型无线自组织网络中的安全组通信提供一个可扩展的解决方案；Xu 等人[11]提出了一种基于区块链和令牌机制的匿名认证动态群组密钥协商方案，用于提高工业5.0 中物联网设备的群组通信效率并降低能耗；Lee 等人[12]提出了一种轻量级的匿名动态群组认证密钥协商方案，使一组医疗传感器设备能够相互认证并协商一个共享会话密钥，用于解决医疗物联网中的传输安全问题.

非对称群组密钥协商由Wu 等人[13]首次提出，他们提出的是一种单轮的非对称群组密钥协商协议（Asymmetric Group Key Agreement，ASGKA），该协议允许1 组用户只协商1 个共同的公共加密密钥，然后每个用户各自计算自己的解密密钥，加密密钥公开，任何人都可见，解密密钥由各用户秘密保存，但该方案不能抵御主动攻击且只适用于成员不发生变化的静态群组；随后，Zhang 等人[14]对ASGKA 协议进行了扩展和改进，设计了一个基于身份的认证非对称群组密钥协商协议，该协议能够抵御主动攻击，且适用于成员可发生变化的动态群组；张启坤等人[15]提出了一种应用于无线传感网络的簇间轻量级非对称群组密钥协商协议，用于建立安全高效的簇间传感器节点之间的群组通信信道；Li 等人[16]提出了一种基于区块链和属性的非对称群组密钥协商协议，该协议实现了协议参与者的访问控制，用于解决工业物联网中的安全通信问题.

群组密钥协商方案虽然能够解决群组密钥的建立问题，但也存在一些劣势.在群组密钥协商方案中，所有参与群组通信的用户都必须参与群组密钥生成过程，这意味着每个参与群组通信的用户都必须执行一些计算，这些计算可能需要消耗大量的时间，并占用大量的内存和处理器资源；而且参与群组通信的用户之间需要进行频繁的消息传递和交互，从而增加通信开销和延迟.此外，如果有任何一个用户无法参与协商，整个协商过程可能会受到影响.

相比之下，群组密钥分发方案能够很好地规避这些劣势.群组密钥分发是由一个被称为群组密钥管理者（group key manager，GKM）的可信第三方确定群组密钥，并安全地将群组密钥分发给群组内所有成员[5]，不需要全部参与群组通信的用户参与到群组密钥的生成过程，用户之间也不需要进行频繁的交互，从而减少了时间、内存、处理器资源的消耗，降低了通信开销和延迟.Guo 等人[17]提出了一种自愈群组密钥分发协议，用于提高物联网不可靠无线网络中群组通信的安全性和效率；Meng 等人[18]提出了一种基于Shamir 秘密共享方案的群组密钥分发协议，该协议将在线和离线概念引入群组密钥分发，从而大幅度提升了群组密钥响应和恢复的速度；Li 等人[19]提出了一种用于无人机自组织网络的互愈群组密钥分发方案，该方案能有效抵御各种攻击；Jiao 等人[20]提出了一种计算高效的群组密钥分发协议，用于解决移动终端在动态群组密钥分发过程中的计算成本问题；Yıldız 等人[21]提出了一种基于物理不可克隆函数和中国剩余定理的轻量级认证群组密钥分发协议，用于解决物联网中的群组认证和密钥管理问题；Xu等人[22]提出了一种应用于车载自组织网络的批量认证群组密钥分发协议，该协议结合了消息批量认证和群组密钥分发，用于确保每个经过认证的车辆都能获得相同的群组密钥.

近年来，大量的群组密钥分发方案都是针对物联网应用场景而设计的，针对即时通讯群聊场景的方案却相对较少.物联网应用场景下，连接到物联网的设备通常资源有限，需要设计轻量级高效的群组密钥分发方案，而且由于设备通常由电池供电，因此要求密钥分发方案不能消耗过多的电力[17]；同时鉴于物联网网络的分布式特性，群组密钥协商比群组密钥分发更适合物联网环境[6].相比之下，在即时通讯群聊场景中，设备通常拥有更高的计算能力和更大的存储空间，因此可以考虑构造更复杂的群组密钥分发方案来建立群组密钥，以保证安全性；而且由于在即时通讯群聊中，通常由群主等具有更高权限的用户来管理群聊，采用群组密钥分发更符合这一特点.

与此同时，群组密钥分发方案通常在可扩展性和效率方面表现更出色，相较于群组密钥协商方案而言也更适用于即时通讯群聊场景.而使用基于身份的密码体制[23]不需要申请和交换公钥证书，可以降低服务器管理密钥的成本，简化服务器管理密钥的流程，适用于即时通讯软件.本文提出了一个基于身份的群组密钥分发方案，旨在解决即时通讯群聊场景下的通信安全问题.本文方案基于国密SM9 算法和多项式进行构造，将群组密钥嵌入到椭圆曲线点与多项式系数中后进行分发；与文献[17-22]中依赖可信第三方分发群组密钥的方案不同，本文方案由群聊中的群主负责生成群组密钥，并将群组密钥分发给群聊内的所有群成员，以此实现了即时通讯群聊场景下的群组密钥分发，保障了通信安全.

本文方案的优势主要包括4 个方面：

1）基于身份的密码体制.采用了基于身份的密码体制，避免了公钥证书机制，降低了密钥管理的复杂性.

2）兼容性较好.本文提出的方案基于国密SM9算法构建，能更好地保障我国政府及企业的通信安全.

3）支持离线操作.在本文提出的方案中，群组密钥分发操作仅要求群主在线，而其他群成员可以在群主分发群组密钥时处于离线状态，无需受到实时在线的限制.在上线之后，他们可使用接收到的信息，按照方案规定的计算方法，有效地获取群组密钥.

4）支持群组密钥恢复.在即时通讯群聊场景下，本文方案支持在服务器上存储群组密钥分发阶段由群主发送的参数，当群成员存储在本地的群组密钥丢失时，可向服务器请求这些参数以恢复丢失的群组密钥.

1 预备知识

1.1 双线性对

设G1和G2是2 个加法循环群，GT是一个乘法循环群，G1，G2，GT的阶均为素数N，P1是群G1的生成元，P2是群G2的生成元，存在G2到G1的同态映射 ψ使得ψ(P2)=P1，双线性对e:G1×G2→GT为满足3 个性质的映射：

1）双线性：对任意的P∈G1，Q∈G2，a，b∈ZN，有e([a]P,[b]Q)=e(P,Q)ab；

2）非退化性：e(P1,P2)≠；

3）可计算性：对任意的P∈G1，Q∈G2，存在有效的算法计算e(P,Q).

1.2 相关困难问题

本文所提方案的安全性基于椭圆曲线计算性DH（elliptic curve computational Diffie-Hellman，ECCDH）问题[24-25]的困难性，ECCDH 问题的定义为：

定义1.ECCDH 问题.设G1是一个N阶的椭圆曲线群，P1是G1的生成元，G1上的ECCDH 问题就是随机选择x，y∈[1,N-1]，给定(P1,[x]P1,[y]P1)，计算[xy]P1.

定义2.ECCDH 假设.设G1是一个N阶的椭圆曲线群，P1是G1的生成元，如果对于数值足够大的安全参数k，任意概率多项式时间的敌手 A满足：AdvECCDH(A)=Pr[A(G1,P1,[x]P1,[y]P1)=[xy]P1]≤ε(k)，其中，AdvECCDH(A)表示敌手 A解决ECCDH 问题的优势，x，y∈[1,N-1]，ε(k)是可忽略的，则称群G1满足ECCDH 假设.

1.3 安全模型

本文借鉴了文献[15,26]中的安全模型，在此基础上给出了本文方案的参与者模型与敌手模型的形式化定义，以及要实现的安全目标.

定义3.敌手模型.本文只考虑被动敌手.通过定义一个挑战者 C 与被动敌手 A之间的游戏来定义敌手模型，该模型中包含1 个群聊的成员（包括群主和普通群成员）的集合和1 个敌手 A，每个群聊成员被模拟成一个随机预言机，该游戏的具体步骤为：

1）系统建立阶段.挑战者 C输入安全参数λ运行系统建立算法，生成系统公共参数的集合params和密钥生成中心（key generation center，KGC）的主私钥ke. C 将params发送给敌手 A，并保存KGC 的主私钥ke.

2）查询阶段.敌手 A可以通过执行查询与挑战者 C进行交互，敌手 A可以进行的查询次数为多项式有界次.

2 基于身份的群组密钥分发方案

本节将介绍本文基于国密SM9 算法提出的一种基于身份的群组密钥分发方案.

本文提出的方案中共有3 个角色，分别是KGC、创建群聊的群主和群内的普通群成员.其中KGC 负责生成系统参数、用户的长期私钥和用户的公开参数；群主负责产生群组密钥并进行分发；普通群成员通过群主发送的参数来计算出群组密钥.假设群主和普通群成员都是向KGC 注册过的、可信任的用户.在本节中将给出本文方案的群组密钥分发阶段、新成员加入群聊阶段和老成员退出群聊阶段的具体过程.

2.1 群组密钥分发阶段

假设存在一个群聊，该群聊由n+1 个用户组成，分别表示为U0,U1,U2,…,Un，其中U0为群主，U1,U2,…,Un则为普通群成员.假设这n+1 个用户均已向KGC注册过且都是可信的.设这n+1 个用户的身份标识符分别为ID0,ID1,ID2,…,IDn.在群聊开始前，为了保障群聊天消息的安全性，这些用户需要共享一个群组会话密钥，用于加密群聊天消息.

2.1.1 系统初始化

在这一阶段，KGC 生成系统参数并为所有注册用户生成其长期私钥和公开参数.需要说明的是，由于本文方案基于国密SM9 算法进行构建，因此这一过程和SM9 算法中系统加密主密钥和用户加密密钥的产生流程[27]相同.

KGC 选择一个大素数p和一个大素数N，然后选择椭圆曲线E(Fp)上的N阶循环子群G1和椭圆曲线E(Fp2)上的N阶循环子群G2；令P1为群G1的生成元，P2为群G2的生成元.接下来KGC 构造一个双线性映射e:G1×G2→GT.

KGC 随机选择一个数ke∈ZN作为主私钥，然后计算Ppub-e=[ke]P1作为系统公钥.随后KGC 选择2 个哈希函数H1:{0,1}*→ZN和H2:GT→Zq，q的值后续由群主来决定，并选择用一个字节表示的加密私钥生成函数识别符hid.KGC 公开{G1,G2,P1,P2,Ppub-e,e,H1,H2,N}作为系统参数，并秘密保存主私钥.

对于每个注册用户Ui，KGC 计算dei=[ke×(H1(IDi||hid,N)+ke)-1]P2作为其长期私钥，计算Qi=[H1(IDi||hid,N)]P1+Ppub-e作为其公开参数，然后通过一个安全的信道将dei和Qi发送给每个用户Ui.当群成员加入群聊时，其对应的Qi会发送给群主U0.

2.1.2 群主生成群组密钥并计算相关参数

此过程将群组密钥由群主生成并分发给群成员.会话开始前，群主首先随机生成一个比特长度为len的整数q，然后随机生成一个比特长度为len的整数K作为群组密钥，要求1 ≤K＜q.

为了将群组密钥K分发给群内的其他n个成员，群主依次执行3 个操作.

1）生成n+1个随机数rk∈[1,N-1]，并计算：

①Ck=[rk]Qk，0 ≤k≤n，Ck∈G1；

②hk=H2(e([rk]Ppub-e,P2))，0 ≤k≤n，1 ≤hk＜q；

2）随机选择R∈[1,q-1]，然后构造多项式，并计算出各项的系数：

3）将C1,…,Cn,an+2,…,a0和q广播给群内的每个成员.

2.1.3 群成员计算群组密钥

群内的每个用户Uj(1 ≤j≤n)在收到携带参数的报文之后，通过3 个步骤计算得到群组密钥K：

1）从报文中提取出Cj,an+2,…,a0和q，然后验证Cj∈G1是否成立，若不成立则报错并退出；

2）计算哈希值hj=H2(e(Cj,dej))；

3）计算群组密钥K：

2.2 新成员加入阶段

假设新用户Un+1,Un+2,…,Un+m想要加入到该群聊中，他们的身份标识符分别为IDn+1,IDn+2,…,IDn+m，长期私钥分别为den+1,den+2,…,den+m，公开参数分别为Qn+1,Qn+2,…,Qn+m.新用户首先会向群主U0提交加群申请，提交申请时会同时发送自己的公开参数.若U0同意他们加入，就依次执行4 个操作.

1）重新生成一个比特长度为len的整数q′，然后随机生成一个比特长度为len的整数K′作为群组密钥，要求1 ≤K′＜q′.

2）重新生成n+m+1个随机数∈[1,N-1]，并重新计算：

3）重新选择一个随机数R′∈[1,q′-1]，然后重新构造多项式并计算出各项的系数：

2.3 成员退出阶段

假设该群聊中有t个用户要退出群聊，那么在这t个用户退出群聊之后，群主U0依次执行4 个操作重新分发新的群组密钥给仍在群内的群成员.

1）重新生成一个比特长度为len的整数q′′，然后随机生成一个比特长度为len的整数K′′作为群组密钥，要求 1 ≤K′′＜q′′.

2）重新生成n-t+1个随机数∈[1,N-1]，并重新计算：

若群主U0退出该群聊且在退出前未将群主权限移交给其它群成员，那么该群聊会立即解散，其余群成员在此之后无法通过该群聊进行通信，也无需重新建立该群聊的新的群组密钥；若群主U0退出该群聊且在退出前将群主权限移交给其它群成员，那么此后将由新群主进行群组密钥分发工作.

3 正确性与安全性分析

3.1 正确性分析

本节分析了本文方案的正确性.正确性是指若群内每个普通群成员计算无误，则计算得到的群组密钥与群主生成的群组密钥一致.

定理1.本文方案满足正确性.

证明.设群主U0生成的群组密钥为K，q为与K比特长度相同且满足1 ≤K＜q的整数，每个普通群成员Ui计算出来的群组密钥为Ki.群主U0为每个Ui计算的hi为：

因此群内每个普通群成员Ui在本地计算出的群组密钥和群主U0生成的群组密钥是同一个密钥.

综上所述，本文提出的方案满足正确性.证毕.

3.2 安全性分析

本节借鉴了文献[15,26,28]对本文方案的安全性进行了分析与证明.

本文方案能够抵抗被动攻击，即一个被动敌手A无法通过监听信道上传输的消息来获取已建立的群组密钥的相关信息.将本文方案的安全性归约到ECCDH 问题上，通过这个困难问题来证明本文方案对被动敌手 A是安全的.

定理2.在1.3 节定义的安全模型下，如果存在一个被动敌手 A能在多项式时间内以不可忽略的优势计算得到本文方案中的群组密钥K，那么就可以利用敌手 A 来构造一个算法 B，使得算法 B能以不可忽略的优势来解决ECCDH 问题.

证明.假设一个被动敌手 A能在本文方案中以不可忽略的优势计算得到本文方案中的群组密钥K.由于本文方案不满足完美前向安全性，群内所有成员的长期私钥不能泄露，因此规定敌手 A无法执行查询与查询.规定 A能执行的查询只有算法 B利用敌手 A构造而来.设算法 B要解决的ECCDH 问题的一个实例为(P1,X=[x]P1,Y=[y]P1)，下面将展示算法 B如何调用敌手 A作为子程序来求解[xy]P1.

假设群聊共有n+1个参与者，其中1 人为群主U0，其身份标识符为ID0，剩下的n个人为普通群成员U1,U2,…,Un，他们的身份标识符为ID1,ID2,…,IDn.定义一个新的会话，该会话有一个唯一的标识符sids，算法 B将sids记录下来.

1）初始化系统.设N是群G1，G2的阶，P1表示群G1的生成元，P2表示群G2的生成元，双线性对e:G1×G2→GT，B首先选取一个随机数ke∈ZN作为系统主私钥，并计算系统公钥Ppub-e=[ke]P1，然后选择一个哈希函数H0作为随机预言机，最后设置系统参数为params={N,G1,G2,P1,P2,Ppub-e,e,H0}，并把params发送给敌手 A.

之后，算法 B按照1.3 节定义3 中定义的游戏与敌手 A进行交互.

①随机生成一个整数q，然后随机生成一个与q具有相同比特长度且满足1 ≤K＜q的整数K；随机选择一个数R∈[1,q-1]，并生成n+1 个随机数ri∈[1,N-1]；

然而定理2 与ECCDH 问题的假设相矛盾，因此由反证法可知，敌手 A赢得游戏的概率是可忽略的.证毕.

4 性能分析

4.1 理论分析

本节从理论的角度分析本文方案的存储开销和通信开销.

假设运行本方案时聊天群内一共有n+1 个用户U0,U1,U2,…,Un，其中U0为群主，其余n个用户为普通群成员.假设每次分发的群组密钥的比特长度都是相等的.

4.1.1 存储开销

表1 显示了本文方案的存储开销.对于群主U0而言，由于rk(0 ≤k≤n)的值是每次分发群组密钥时随机选取的，Ck，hk(0 ≤k≤n)则是每次分发群组密钥时根据rk计算出来的，an+2,an+1,…,a0的值是每次分发群组密钥时根据hk构造而来的多项式的系数，这些值在每次进行群组密钥分发时都是不一样的，因此群主无需存储这些临时数据.群主需要存储的只有自己的长期私钥de0、群内n+1 个用户的公开参数Qk和每次分发的群组密钥K.由2.1.1 节可知，Qk是椭圆曲线E(Fp)上的点，它可被压缩成一个长为个字节的字节串之后再进行存储[29]；而de0是椭圆曲线E(Fp2)上的点，它可以被压缩成一个长为个字节的字节串后再进行存储[29].综上可得，群主每次运行该方案时的存储开销为+n+2个字节.

Table 1 Storage Cost of Our Scheme表1 本文方案的存储开销

对于每个普通群成员而言，需要存储的只有长期私钥、公开参数和每次群主进行群组密钥分发时计算出来的群组密钥.因此每个普通群成员每次运行该方案时的存储开销为个字节.

4.1.2 通信开销

表2 显示了本文方案的通信开销.每次分发群组密钥时需要传输的数据是群主广播的参数an+2,an+1,…,a0和C1,C2,…,Cn以及q，其中ai∈[1,q-1](0 ≤i≤n+2)，长度为lb(q-1)个比特，C1,C2,…,Cn均为椭圆曲线E(Fp)上的点，这些点可以分别被压缩成一个长度为个字节的字节串后再进行传输，因此本文方案的通信开销为个字节.

Table 2 Communication Cost of Our Scheme表2 本文方案的通信开销

4.2 时间性能仿真实验分析

本节通过仿真实验对本文方案的时间性能进行了分析.

实验中使用C++实现本文方案.选择国密SM9标识密码算法的曲线参数来实例化本文方案的系统参数，参照SM9 算法标准文档中定义的哈希函数来实现本文方案中的哈希函数H1和H2，调用gmssl 库函数执行点乘、点加和双线性对运算，使用gmp 库进行大数模乘、模加、模幂运算.测试平台配置为11th Gen Intel®Core™ i7-11 700 @ 2.50GHz × 2 的处理器，4 GB 的内存，Ubuntu 20.04.6 LTS 版本的64 位操作系统.

仿真选择群主计算相关参数所需的平均时间和每个普通群成员计算出群组密钥所需的平均时间作为评价指标，固定q与K的比特长度为128，分析当普通群成员人数n逐渐增大时对这2 个评价指标的影响.

本文方案中涉及6 种不同的运算，因此首先通过测试获得了这6 种运算各自所需的平均时间，结果如表3 所示，其中 Zq表示模q的整数环.

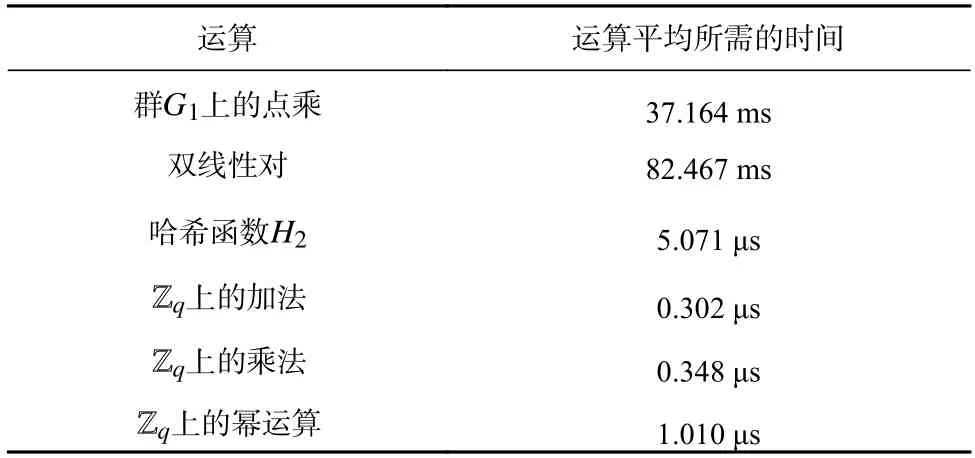
Table 3 Average Time Required for Each of the Six Operations表3 6 种运算各自所需的平均时间

从表3 中可以看到，本文方案的时间开销主要来自于双线性对运算和群G1上的点乘运算.对于哈希函数H2，虽然其实现过程较为繁琐，但由于不涉及复杂的运算和循环操作，因此执行时间很短，而 Zq上的大数加法、大数乘法、大数幂运算在gmp 库的实现所花费的时间几乎可忽略不计，因此执行后4 种运算所需的平均时间远小于前2 种运算.

图1 给出了当普通群成员人数增大时群主计算相关参数所需时间的增长情况.随着人数的增加，群主需要计算的Ck，hk，ak的数量也随之增加，要执行的双线性对运算次数和G1上的点乘运算次数也增加，从而导致计算所花费的时间增加.从图1 中可以看到，当人数超过70 时，群主计算所花费的时间超过了10 s，当人数超过450 时，群主计算所花费的时间超过了60 s.

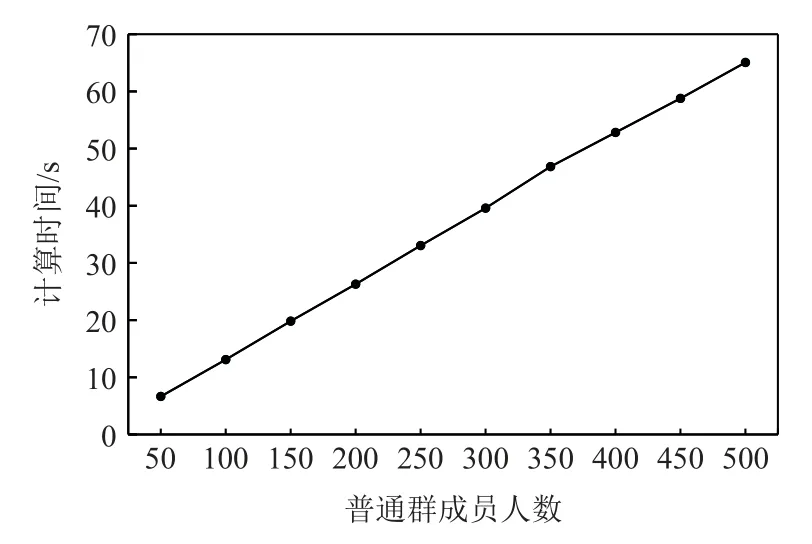
Fig.1 Average time required for the group owner to calculate the relevant parameters图1 群主计算相关参数所需的平均时间

图2 给出了当普通群成员人数增大时每个普通群成员计算出群组密钥所需的平均时间的变化情况.如图2 所示，当普通群成员人数逐渐增大时，每个普通群成员计算出群组密钥所需的平均时间的变化幅度很小，而且即使人数增长到500，计算时间仍然不超过0.1s，时间开销完全在用户可接受的范围内.这是由于每个普通群成员每次执行该方案时只需计算1 个hj，计算量的增加仅仅是由于 Zq上的大数加法、大数乘法、大数幂运算的运算次数增加而导致的，而如表3 所示，这3 种运算的执行时间很短，因此带来的时间消耗并不会大幅度增长，只会引起很小的变化.

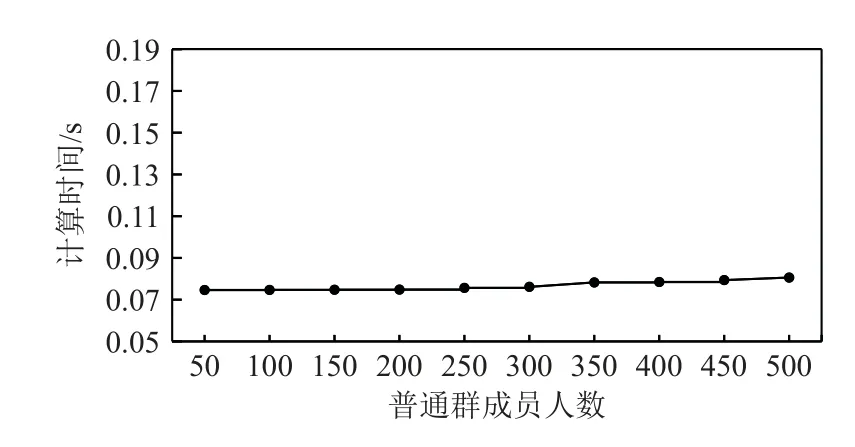
Fig.2 Average time cost for each ordinary group member to calculate the group key图2 每个普通群成员计算出群组密钥的平均时间开销

由图1 和图2 可知，本文方案在小规模群组中表现良好，但应用到大规模群组中时会出现群主分发密钥时间较长的问题，但这种额外的时间代价是为了保障群聊消息的机密性而不可避免的.在实际应用中，通常情况下只需在建群之初运行一次本文方案，如果后续需要更新群组密钥，只需令全群禁言并运行一次本文方案来重新分发群组密钥.因此，相对于整个群聊会话的持续时间而言，本文方案所需的时间并不多.

当有新成员加入或有老成员退出时，群主需重新运行一次本文方案计算出新的群组密钥，这种情况下带来的计算开销取决于群成员发生变动后群内共有的群成员数量.如图1 所示，若群成员发生变动后群内成员总人数超过200，那么群主重新计算出新的群组密钥所花费的时间会超过30 s.但是通常情况下群组成员并不会频繁发生变动，因此群主不需要经常重新执行本文方案，也无需频繁进行大量的计算操作.

综上所述，为了保证群聊通信的安全性，本文方案产生的时间开销是可以接受的.

4.3 方案的对比

本节从群组密钥分发者的身份、预共享参数需求、群组成员交互需求和兼容性4 个方面将本文方案与文献[17]方案、文献[18]方案进行了对比，比较结果如表4 所示.其中分发者指的是负责产生群组密钥并进行分发的实体，接收者指的是负责接收相关参数并计算出群组密钥的实体.

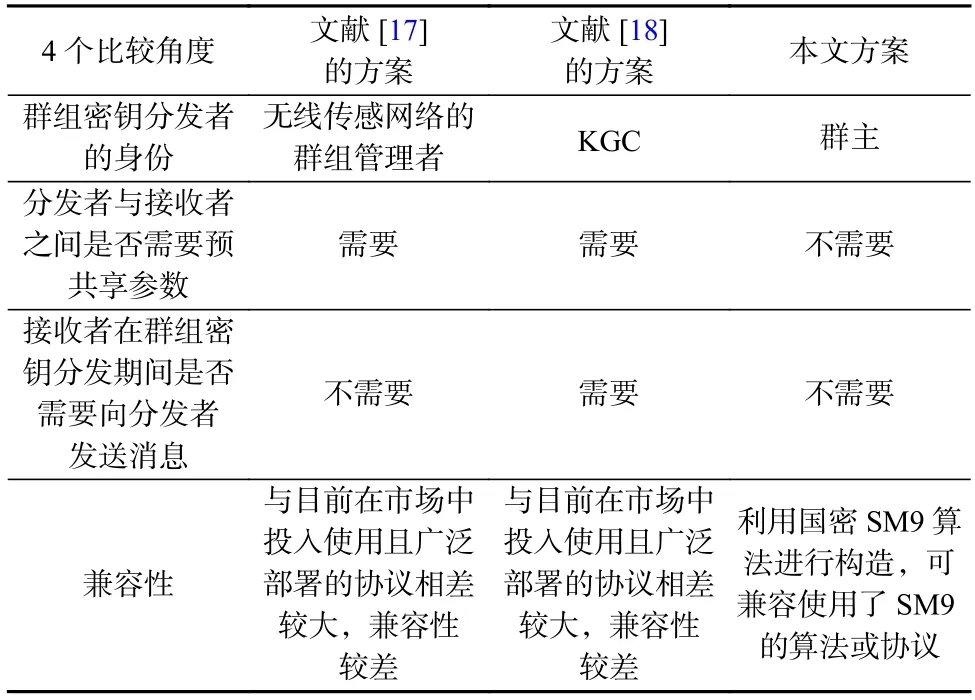
Table 4 Comparison Between Our Scheme and Other Schemes表4 本文方案与其他方案的比较

从表4 中可以看出，相比于另外2 个方案采用可信第三方来分发群组密钥，本文方案采用的是群组内具有更高权限的用户来分发群组密钥，赋予用户更多的自主决策权，使得用户可以控制群组密钥的产生与分发，从而保证只有群组内成员能够读取群聊消息明文，而除了群组成员之外的任何人，包括服务提供商都无法读取聊天内容的明文；相比于另外2 个方案，本文方案中接收者在群组密钥分发阶段之前不需要与分发者共享任何参数，这意味着接收者与分发者需要存储和管理的参数更少，减轻了接收者与分发者的参数管理负担；相比于文献[18]方案中接收者在群组密钥分发阶段还需要额外向分发者发送消息，本文方案中在群组密钥分发阶段只有群主需要向群成员发送消息，而群成员无需再向群主发送任何消息，这意味着本文方案具有更少的交互和更低的通信成本；在兼容性方面，本文方案能兼容现有的算法标准，具有更好的兼容性.

本节还从密钥管理的4 个角度和兼容性比较了本文方案与文献[13]的方案，比较结果如表5 所示.

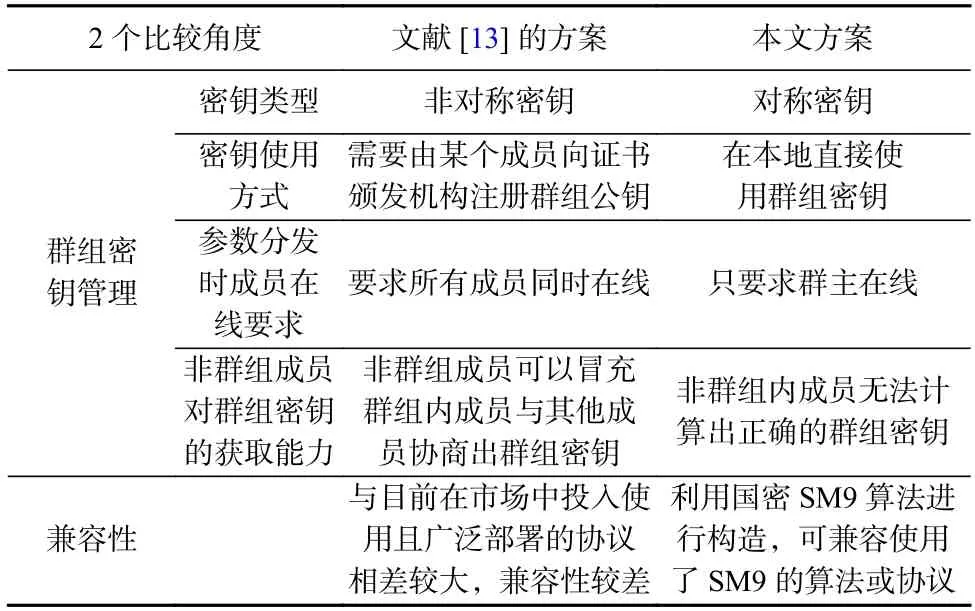
Table 5 Comparison Between Our Scheme and the Scheme Proposed in Reference [13]表5 本文方案与文献[13]方案的比较

从表5 中可以看出，本文方案在群组密钥管理上比Wu 等人的方案更有优势，因为本文方案中无需向证书颁发机构注册群组密钥，简化了密钥管理的流程，密钥分发的过程中也不要求除群主外的所有群成员都在线，灵活性更高；同时由于本文方案利用了SM9 算法进行构造，可以使用SM9 算法的国家标准来实现，兼容性更好，能够更好地满足国内的政府和企业对群聊通信安全的需求.

5 本文方案在具体场景下的应用

本节将详细描述本文方案在具体场景下的应用方式.首先展示本文方案应用到一个具体的即时通讯群聊场景中时的运行流程；然后简要介绍本文方案的一个外延应用，即本文提出的群组密钥分发方案是如何在点对点通信场景下转换成非对称加密算法来进行端到端加密的；最后将本文简要介绍的即时通讯软件所采用的方案与本文方案进行对比，指出其不足之处，展现本文方案的优势与创新点.

5.1 本文方案在即时通讯群聊场景下的运行流程

5.1.1 场景描述

假设某公司为了防止外人窃取公司数据而导致公司的机密信息泄露，打算开发一款局域网即时通讯软件来进行公司内部员工之间的交流，让公司内部产生的消息只在公司的局域网内流动，从而保证公司数据的安全.该公司有多个部门，每个部门人员较为固定，不会发生很大的变动，为了满足部门内部的团队沟通协作、发布通知公告等需求，该公司计划在软件中加入群聊功能，由部门领导创建群聊，部门其余员工加入群聊.为了保障这一功能的安全性，同时为了保证通信效率，需要对群聊消息采取对称加密措施，此时如何让群内所有用户共享一个加解密群聊消息的对称密钥成为一个关键问题，在这种情况下，可以应用本文方案来解决这一问题.

5.1.2 方案应用

本节将详细描述如何应用本文方案解决5.1.1 节所述的场景描述下的问题.假设公司内部员工都是可信的.

该公司内部人员首次使用他们的局域网即时通讯软件时会先进行注册.每个用户Ui注册时软件客户端会将用户身份信息发送给局域网内的服务器，服务器为Ui生成其身份标识符IDi、公开参数Qi和长期私钥dei，其中IDi作为公开信息与Ui的账号绑定，然后将IDi，Qi，dei发送给Ui，同时保存IDi，Qi，dei.这一过程如图3 所示.

Fig.3 Company employees register图3 公司员工注册

为了方便部门内发布公告、沟通工作事宜，某部门领导U0会作为群主创建群聊，然后将当前在该部门工作的全体员工加入群聊，初次创建群聊时，这一操作会强制将当前该部门所有的在职员工加入群聊.假设创建群聊时该部门除U0外共有n个在职员工U1,U2,…,Un，他们的身份标识符分别为ID1,ID2,…,IDn.由于每个员工的身份标识符与其账号绑定，因此创建群聊时U0的客户端会提交目前该部门所有在职员工的IDi(0 ≤i≤n)给服务器，然后服务器会为这个群聊创建一个唯一的群标识符group_ID，并返回group_ID和IDi(1 ≤i≤n)对应的Qi的值给U0，同时保存group_ID和群主U0的身份标识符ID0，这一过程如图4 所示.在U0的客户端按2.1.2 节分发密钥之前，部门群处于禁言状态，所有群成员在此时均不可发布聊天消息.

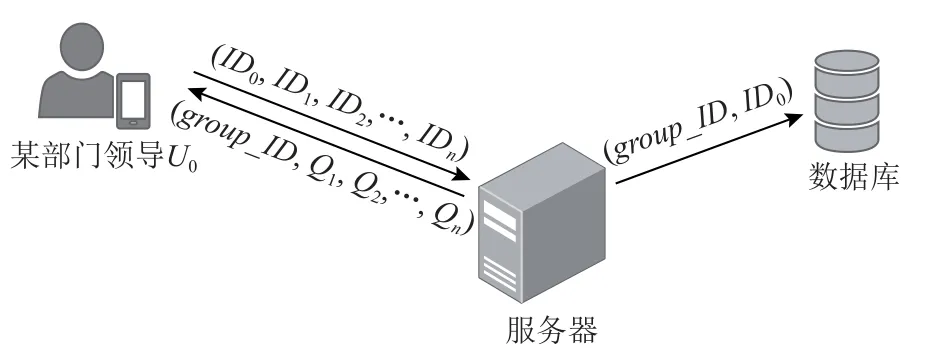
Fig.4 Department leader creates group chat图4 部门领导创建群聊

接下来U0的客户端先在本地随机生成一个比特长度为len的整数q，然后随机生成一个比特长度为len且满足1 ≤K＜q的整数K，将K作为群组密钥，按2.1.2 节所述的方式计算出C0,C1,…,Cn和an+2,an+1,…,a0.为了在公司的服务器上备份这些参数以供群内所有用户恢复本地丢失的群组密钥，U0的客户端会1）先将(group_ID,compute_params,(ID0,C0),(ID1,C1),…,(IDn,Cn),an+2,an+1,…,a0,q)以某种格式封装成报文，其中group_ID标识该报文来自于该部门群，compute_params用于表示该报文携带的是用于计算该部门群的群组密钥的参数；2）将这条报文发送到服务器，由服务器将这条报文发送给其他群成员.群内的每个员工Ui收到这条报文之后对该报文进行解析，首先group_ID和compute_params理解该报文携带的数据的来源与含义，然后将自己的IDi依次与(ID0,C0),…,(IDn,Cn)进行比较，得到相应的Ci以及an+2,an+1,…,a0和q的值，最后按2.1.3 节中给出的3 个步骤计算出群组会话密钥K；服务器在转发这条报文的同时会对报文进行解析，提取并保存group_ID，(IDi,Ci)(0 ≤i≤n)，ai(0 ≤i≤n+2)和q.这一过程如图5 所示.参数发送完毕之后，部门群解除禁言.

Fig.5 Group key distribution图5 群组密钥分发

在客户端计算出群组密钥K之后，Ui(1 ≤i≤n)即可在群里发送消息，消息经过K加密之后在局域网内传输.为了在公司的服务器上备份聊天记录，部门群内的每个人在发送消息时，客户端会将携带消息密文的报文发送给服务器，由服务器将报文转发给群内的其他人，同时解析报文，提取并保存其中携带的数据.这一过程的一个具体示例如图6 所示.

Fig.6 Group members send group chat messages图6 群成员发送群聊消息

该部门群创建之后，新入职该部门的员工可选择申请加入或被U0邀请加入群聊，新员工进群时，U0设置群为禁言状态，然后U0的客户端会重新生成一个群组密钥，按照2.2 节所述的方式重新计算参数并按图5 所示的方式发送参数，参数发送完毕之后，部门群解除禁言；若该部门有员工离职，则由U0强制将离职员工的账号移出群聊，在此期间U0设置群为禁言状态，然后U0的客户端会重新生成一个群组密钥，按照2.3 节所述的方式重新计算参数并按图5 所示的方式发送参数，参数发送完毕之后，部门群解除禁言.

若该部门某员工Ui(0 ≤i≤n)的客户端保存在本地的群组会话密钥K丢失，他所使用的终端会向服务器发送查询请求，服务器会返回用于计算K的相关参数给Ui的客户端，这一过程如图7 所示.

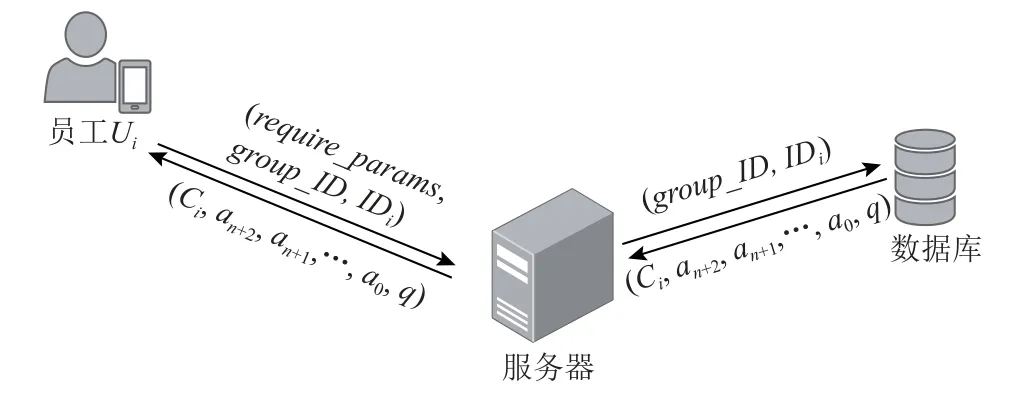
Fig.7 Group members query the server for the relevant parameters used to calculate the group key图7 群成员向服务器查询用于计算群组密钥的相关参数

同理，当Ui存储在本地的群聊天记录丢失时，也可以向服务器发送查询请求，获得相关的聊天记录密文后在本地解密即可.以Ui查询身份标识符为ID2的用户发送的全部群聊消息为例，如图8 所示.

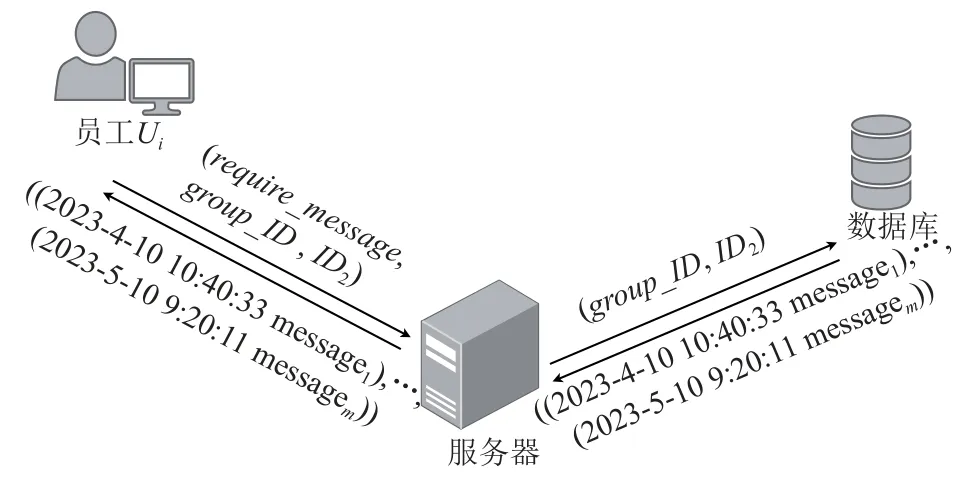
Fig.8 Group members query the server for group chat records图8 群成员向服务器查询群聊记录

5.2 本文方案在点对点通信场景下的应用

本文方案还可以直接应用于点对点通信场景下作为一种端到端加密算法.本节将介绍本文方案是如何作为一种端到端加密算法来运行的.

在点对点通信场景下，参与通信的只有两方.设参与通信的两方为用户U1和用户U2，二者对应的公开参数与长期私钥分别为(Q1,de1)和(Q2,de2)，以用户U1向用户U2发从一条消息为例.设用户U1要发送的消息为M，U1首先随机生成一个整数q，然后通过某种编码方式将M编码成一个与q比特长度相同且满足1 ≤L＜q的整数L；接着U1生成2 个随机数r1,r2∈[1,N-1]，并计算C1=[r1]Q1,C2=[r2]Q2和哈希值h1=H2(e([r1]Ppub-e,P2)),h2=H2(e([r2]Ppub-e,P2))，然后U1随机选择R∈[1,q-1]，构造多项式，并计算出各项的系数：

以上操作相当于对L进行加密.最后U1将C2,a3,a2,a1,a0和q发送给U2.U2在收到这些参数之后，首先验证C2∈G1是否成立.若不成立则报错并退出；若成立，U2首先计算哈希值h2=H2(e(C2,de2))，然后通过计算解密得到：

最后将L解编码成消息M即可得到原始明文.

5.3 即时通讯软件采用方案的对比

本节调研了目前市面上流行的一些即时通讯软件加密群聊通信所使用的协议.由于许多主流的即时通讯软件都没有公布加密群聊消息所采用的协议的细节，因此本节只选取了Signal，WhatsApp 和Facebook Messenger 这3 款公布了群聊加密协议细节的即时通讯软件进行分析.

Signal，WhatsApp 和Facebook Messenger 利用了端到端加密通讯协议Signal 来实现群聊消息加密[30-32]，Signal 协议实现群聊消息加密的大致流程如图9所示[31-32].

Fig.9 Process of implementing group chat message encryption in Signal protocol图9 Signal 协议中实现群聊消息加密的流程

假设群组内共有n+1名成员.由图9 可知，为了得到加解密群聊消息的消息密钥，Signal 协议中每个用户需要首先产生1 个链密钥和1 对签名密钥，再发送n条加密消息将链密钥和签名公钥分别发送给群组中的其他用户，并存储由其余n个用户发来的链密钥和签名公钥，而且每次发送和接收消息时都需要从链密钥中派生出消息密钥并更新链密钥，这些操作不仅会增加用户客户端的计算开销和通信开销，而且会加重客户端的密钥存储和管理的负担，因为每个客户端都需要维护和管理大量的密钥信息.

相比之下，本文方案流程更简单，且能够减轻客户端在密钥存储和管理方面的负担.为了更直观地展示本文方案与Signal 协议中进行群聊加密所采取方法的差异，以及更好地评估本文方案的实用性，表6对比了本文方案和Signal 协议采取的方法.2 种方法都假设群内共有n+1个成员.

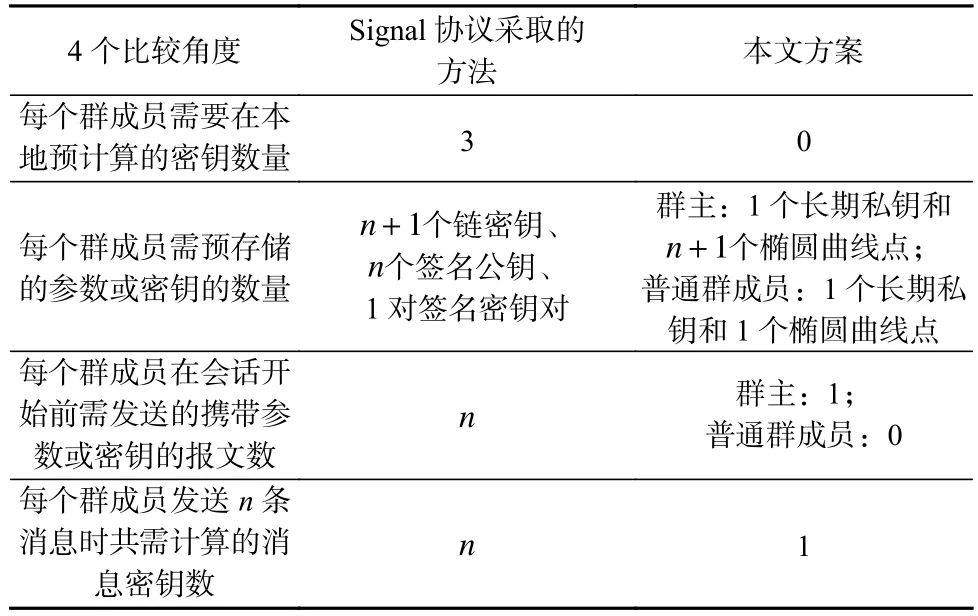
Table 6 Comparison Between Our Scheme and the Method Adopted by Signal Protocol表6 本文方案和Signal 协议采取的方法的对比

如表6 所示，与现有的方案对比之后，综合而言，当应用于实际场景下时，本文方案具有5 点创新点和优势：

1）本文方案采用了基于身份的密码体制生成用户的长期私钥，相比于Signal 协议采取公钥基础设施（public key infrastructure,PKI）进行群组用户的密钥管理，本文方案消除了对公钥证书的依赖，简化了用户密钥的管理问题；

2）在群组密钥管理上，相比于Signal 协议中实现群聊消息加密时需要存储多个消息密钥，本文方案中群组内每个用户在本地客户端只需存储1 个用于加解密群聊消息的密钥，只有群主更新群组密钥时才需要增加存储新的群组密钥，降低了存储开销，减轻了客户端管理群组密钥的负担；

3）在通信开销上，相比于Signal 协议中实现群聊消息加密时每个用户在通信开始前要向群内其他所有用户单独发送消息，本文方案在群组密钥分发阶段只有群主需要向其他群成员广播1 次参数，而每个普通群成员则不需要与其他群成员进行交互，降低了通信开销；

4）应用于实际场景时，本文方案可以做到在客户端不存储参数的情况下恢复丢失的群组密钥.如图7 所示，当群成员客户端存储的群组密钥丢失时，可以向服务器发送参数请求报文，获取存储在服务器端的参数之后在本地重新计算出群组密钥.

5）本文方案在n=2 时可直接用于点对点通信场景下的端到端加密.

6 总结与展望

本文基于国密SM9 算法提出了一种应用于即时通讯群聊场景下的基于身份的群组密钥分发方案，并给出了严格的安全性证明；同时，对所提出的方案进行了存储开销、通信开销的理论分析，并对时间开销进行了仿真实验分析.将本文方案与文献[17-18]的方案进行了对比，发现本文方案在便捷性和兼容性上更具有优势；并与文献[13]提出的ASGKA 方案进行了对比，发现本文方案在密钥管理和兼容性上更具有优势.本文方案可以应用于即时通讯软件的群聊加密场景，在这一场景下本文方案相比于已应用于商业软件的方案而言具有一定的创新性和优势，同时本文方案可以直接用于点对点通信场景下的端到端加密.未来的工作可围绕进一步提升方案的安全性和计算效率这两方面展开.

作者贡献声明：王后珍提出了算法思路和实验方案；秦婉颖负责完成实验并撰写论文；刘芹、余纯武、沈志东提出了实验方案的优化与改进.