无线传感器网络中基于时间窗的无人机数据收集方案
2023-10-26牛涵琨
牛涵琨,朱 江
(重庆邮电大学 通信与信息工程学院,重庆 400065)
0 引 言
随着物联网的不断发展,无线传感器网络(wireless sensor network,WSN)得到了更广泛应用。WSN通常由许多电池供电的传感节点 (sensor node,SN)组成。在某种特定地理区域,用SN来传感和传输传感信息。由于传感节点具有灵活部署和协同工作的优点,无线传感器网络已经应用于许多场景,例如灾害检测[1]、分布式估计[2]和环境监测[3]等。在传统无线传感器网络中,传感节点感知的数据以一跳或者多跳的方式传递给Sink节点,这种方式在传输数据时容易造成能量空洞问题,即靠近Sink节点的SN通常需要更频繁地传输数据,导致该节点的能耗过早耗尽,造成网络断链。因此,引入无人机来解决这个问题[4-5]。与传统的无线传感器网络相比,无人机可以更快地收集数据[6],并且缩短数据收集的时延。此外,无人机与地面上的SN可以建立视距(line of sight,LOS)连接,飞得更接近传感节点,从而建立更稳定的通信链路。因此,与传统无线传感器网络相比,无人机对无线传感节点数据收集更加节能和稳定[7],并且延长了无线传感器网络寿命[8]。
在无人机数据收集的研究中,针对特定的应用场景和不同的优化目标,一些文献提出了基于时间窗的数据收集方案。文献[9]基于收集数据的及时性,提出了时间窗的概念——物联网设备需要及时上传收集到的数据,否则数据将丧失了时效性,但没有优化无人机和传感节点的能耗,导致总系统能耗过高。文献[10]基于内存有限的无线传感节点,提出了时间窗的概念——传感节点需要及时上传数据,否则数据被会新数据覆盖,造成数据丢失。但文献[10]中无人机采用的悬停收集方式未优化无人机的速度,造成过多能耗损失。由此可见,目前基于时间窗的数据收集方案研究大多没有专门考虑无人机和无线传感节点的能耗问题。然而在系统中,能耗是决定系统正常运行的关键因素:无人机飞行能耗决定了无人机的续航时间[11];传感节点能耗决定了传感节点的使用寿命[7,12]。所以,降低系统能耗是相关研究的重点。
为此,本文贡献在于根据无线传感节点MAC层的休眠-活跃调度机制,定义时间窗,并基于此提出了一种无人机轨迹和传输调度的联合优化方案,以降低无人机和无线传感节点的总能耗。联合优化方案是整数非凸问题,为此,首先将传输调度连续化,将混合整数非凸问题转化为连续非凸问题;然后通过引入2个松弛变量,将问题转化为易于求解的凸问题,并利用连续凸逼近法求解。
1 系统模型
系统模型如图1所示,其中无人机在各个传感节点活跃期内收集其数据。此模型可从网络模型、信道模型和能耗模型三个主要方面进行描述。
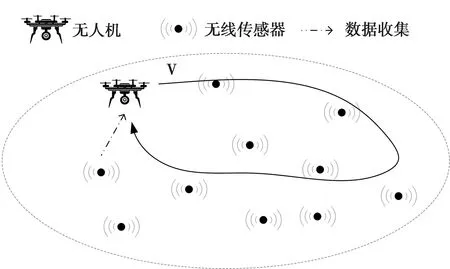
图1 系统模型图Fig.1 System model diagram
1.1 网络模型
地面共有K个传感节点,其集合表示为{1,2,…,K}。无人机总飞行时间为T,本文采用时分多址(time division multiple access,TDMA)方案收集数据。将时间[0,T]离散化为N个相等的时隙,即T=Nδt,其中,δt表示时隙长度,并取值足够小。
利用三维欧几里得坐标表示的方法,可以分别表示出无人机和无线传感节点的具体位置。传感节点分布在地面上,第k个传感节点的位置表示为
wk=(xk,yk,0),k∈{1,2,…,K}
(1)
由于时隙δt足够小,假设与所有传感节点到无人机的距离相比,无人机在δt内的位置变化可以忽略不计,并以固定高度H在空中飞行,连续的无人机轨迹可以离散为N个时隙,在第n个时隙无人机位置表示为
q[n]=(x[n],y[n],H),1≤n≤N
(2)
无人机从起点出发最后回到起点,无人机起始和终止的位置满足q(0)=q(T)。无人机在飞行过程中的最大速度为Vmax,其速度约束可表示为
(3)
假设无线传感器网络在MAC层具有“休眠-活跃”调度机制,每个传感节点有自己的周期性休眠和活跃时间表,传感节点只有在活跃期内才能上传数据,并将其定义为时间窗,如图2所示。如果在时隙n内,节点k始终处于活跃状态,那么该时隙就是节点k的时间窗。图2中,给出3个传感节点的时间窗,传感节点SN1在第3个时隙到第5个时隙处于活跃状态,则该时隙内为传感节点SN1的时间窗,传感节点SN2的时间窗为第5个时隙到第8个时隙,传感节点SN3的时间窗为第9个时隙到第12个时隙。只有在这个时间窗内传感节点才能传输数据,每个传感节点需要传输的数据量为Sk。第k个无线传感节点的时间窗定义为

图2 传感节点的时间窗Fig.2 Time window of sensor nodes
Wk[n]∈{0,1}∀k,n
(4)
(4)式中:Wk[n]=1表示SNk在第n个时隙处于活跃状态;Wk[n]=0表示SNk处于休眠状态,该状态下无法传输数据。
在传感节点活跃状态下,无人机向传感节点发出信号,传感节点接受到信号并开始向无人机传输数据。第n个时隙无线传感节点的传输调度xk[n]为
xk[n]={0,1}∀k,n
(5)
(5)式中,xk[n]=1表示uk在第n个时隙以恒定的发射功率Pk传输数据,否则为xk[n]=0。
无线传感节点只有在活跃状态下才能上传数据,则有
xk[n]≤Wk[n],∀k,n
(6)
由于无人机采用时分多址方案收集数据,在每个时隙内,无人机最多只能收集一个无线传感节点的数据。
(7)
1.2 信道模型
假设无人机与地面传感节点之间的通信信道为准静态衰落信道,其中无人机与无线传感节点之间的信道系数在每个时隙内保持不变,在不同时隙内发生变化。无人机移动性而产生的多普勒效应可以由接收机端补偿,在第n个时隙无人机与第k个无线传感节点的大尺度信道功率增益表示为
(8)
(8)式中,ρk[n]是小尺度衰落的复值随机变量,βk[n]是大尺度衰落系数。其中,大尺度为LoS链路,取决于无人机和无线传感节点的距离,表示为
(9)
(9)式中:β0表示距离为1 m时的信道功率增益,α≥2为路径损耗指数;dk[n]为无人机和第k个无线传感节点的距离;‖·‖表示欧式范数。
小尺度衰落为Rician衰落模型[13]。|ρk[n]|2的累积分布函数表示为
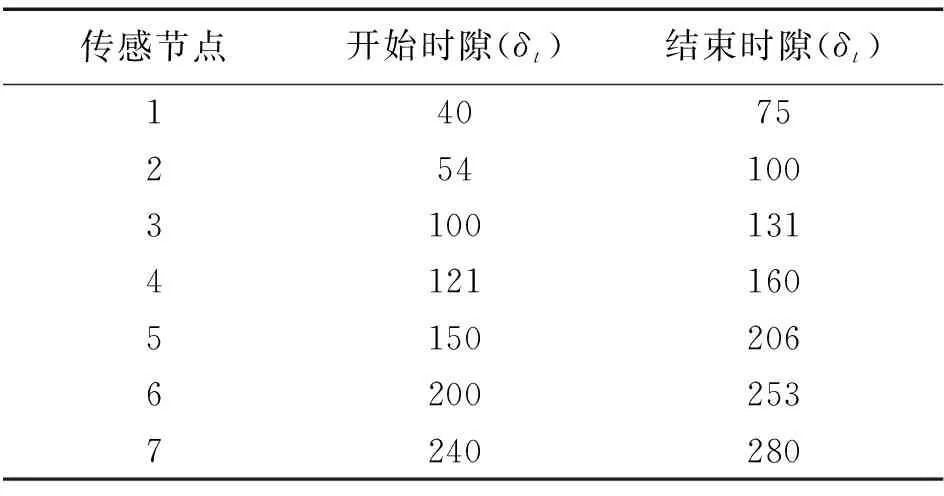
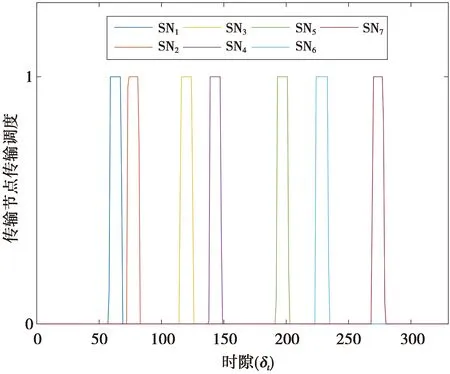
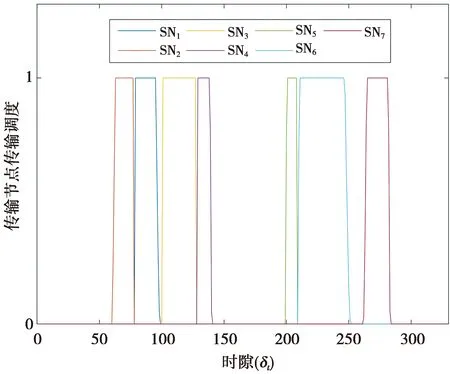
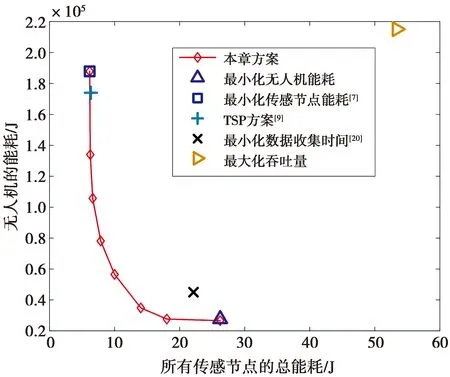
F(z)≜P(|ρk[n]|2 (10) (10)式中,Q1(·)表示0阶修正贝塞尔函数I0的Marcum-Q函数,Rician因子Kc为LoS信号分量与散射分量之间的功率比。 在第n个时隙内,第k个无线传感节点与无人机进行通信,其传输速率(bit/s)为 (11) pk[n]=P(Ck[n] (12) (13) 模型中采用旋翼无人机,无人机能量消耗包括推进能耗和通信能耗,由于是上行数据采集,无人机的通信能耗可以忽略。通过将无人机飞行时间离散化,由文献[14]推导,无人机飞行能耗模型可表示为 (14) (14)式中:P0和Pi是无人机悬停状态下型阻功率和诱导功率;Utip是叶尖角速度(m/s);v0是悬停时平均旋翼诱导速度(m/s);d0是机身阻力比;s是总叶片面积和叶片扫过面积的比;A是无人机叶片扫过的面积(m2);ρ是空气密度(kg/m3)。 由于无线传感节点的电路功率较传输功率较小,本文不予考虑[15]。因此,第k个无线传感节点SNk的能量消耗可以表示为 (15) (16) (16)式中,0≤θ≤1为权衡无人机能耗和传感节点能耗的权重因子。 在满足每个无线传感节点的数据收集要求的前提下,通过联合优化无人机轨迹Q≜{q[n]}和传感节点传输调度X≜{xk[n]} ,最小化无人机飞行能耗与所有传感节点总能耗的加权和Dθ。根据上述模型,这个优化问题可表示为 C3:xk[n]∈{0,1},∀k,n C4:Wk[n]∈{0,1}∀k,n C5:xk[n]≤Wk[n],∀k,n C6:‖v[n]‖≤Vmax,1≤n≤N-1 C7:q[1]=q[N] (17) (17)式中:约束C1表示每个传感节点需要传输完数据;约束C2表示在一个时隙内无人机只能收集一个传感节点的数据;约束C3表示无线传感节点的数据传输调度;约束C4表示传感节点休眠-活跃状态;约束C5表示无人机必须在传感节点活跃状态下才能收集数据;约束C6表示无人机飞行的最大速度;约束C7表示无人机完成任务后必须飞回起始点。 由于存在二进制变量xk[n]和非凸约束C1,且目标函数中飞行能耗也是非凸的,问题P1是混合整数非凸问题,难以求解。为此,提出了一种基于(successive convex approximation,SCA)的求解方法。 针对P1是混合整数非凸问题,提出一种基于SCA的迭代算法来求解原问题的次优解。为了将问题P1转化为一个凸问题,首先将二进制变量松弛为连续变量将原问题转化为连续非凸问题,然后引入2个松弛变量并进行变换,将连续非凸问题转化为凸问题,最后对凸问题求解。 首先要处理问题P1中的混合整数约束,将C3中的二进制变量松弛为连续变量,得到 s.t. C1,C2,C4-C7 (18) C8:0≤xk[n]≤1,∀k,n 混合整数非凸问题P1转化为连续非凸优化问题P2,依然很难求解。 对于问题P2连续非凸优化问题,其中飞行能耗和约束条件C1是非凸的。为了将P2转变为凸问题,首先引入松弛变量Y={y[n]≥0},其中 (19) (19)式可等价为 (20) 给定第r次迭代的局部点vr[n]和yr[n],由于‖v[n]‖2和y[n]2分别关于v[n]和y[n]的凸函数,因此,(20)式右端可以通过一阶泰勒展开表示下界,令φ[n]表示其下界函数,则有 (21) 因此,无人机飞行能耗可重写为 (22) gk[n]≤Rk[n] (23) (xk[n]+gk[n])2≥ (24) 由(23)式,以下不等式成立 (25) (25)式将约束C1转化为凸约束。此时,(23)式为非凸的,同理对(23)式中的Rk[n]一阶泰勒展开,则有 wk‖2+Ik,r[n]‖qr[n]-wk‖2 (26) (26)式中: (27) (28) Jk,r[n]=H2+‖qr[n]-wk‖2 (29) 引入松弛变量后,通过对松弛变量y[n],gk[n]的变换将非凸问题P2转化为凸问题P3。 s.t. C2,C4-C8 C9:y[n]≥0,∀n C10:gk[n]≥0,∀n,k (30) 算法1基于SCA的求解算法 1.初始化无人机轨迹Q0,传输调度X0,设置算法收敛阈值ε1,迭代次数r=0。 3.forr=0,1,2K 5.更新xr+1[n]=x*[n],Rr+1[n]=R*[n],vr+1[n]=v*[n],yr+1[n]=y*[n],gr+1[n]=g*[n],qr+1[n]=q*[n] 6.判断|Dθ(xr+1,Rr+1,vr+1,yr+1,gr+1,qr+1)-Dθ(xr,Rr,vr,yr,gr,qr)|≤ε1,成立进入步骤8,否则返回步骤3 7.更新r=r+1 8.end for 9.得到结果。 在算法1中,每次迭代都会求解标准凸优化问题P3,优化变量Q和X仅与传感节点个数K和无人机飞行的总时隙数N有关,算法1执行了L次迭代,因此其复杂度是O{LK3.5N3.5log(1/ε1)},其中,ε1是算法精度。由于所提方案嵌入了SCA的算法,此算法本身是收敛的[16],所以,所提方案是收敛的,且可以收敛到满足P1的Karush-Kuhn-Tucker(KKT)条件的KKT解[17]。所提方案的计算过程不需要在无人机上运行,可以在地面工作站离线实施。然后,将运行结果Q和X从地面工作站上传到无人机,无人机就可以按照这些结果开始数据收集任务。 考虑一个二维区域,其中7个传感节点随机分布在区域内且位置已知,单架无人机在恒定的高度H=100 m。无人机端的加性高斯白噪声设置为σ2=-110 dB,在距离d0=1 m时的参考信道功率增益β0=-60 dB。无人机的最大飞行速度Vmax=50 m/s;飞行周期T=164 s。时隙长度δt=0.5 s;带宽B=1 MHz;权重参数λ=1 000。对于传感节点,假设每个传感节点具有相同的发射功率Pk=0.1 W,每个传感节点需上传数据量Sk=50 MByte,其时间窗参数如表1所示。对于旋翼无人机的推进能耗参数[11]为d0=0.6;Utip=120;A=0.503;ρ=1.225;s=0.05;P0=79.86;Pi=88.63;v0=4.03 m/s。 表1 传感节点的时间窗Tab.1 Time window of sensor nodes 本文考虑大多数场景下,传感节点具有休眠-活跃周期,传感节点需在活跃期内上传数据,休眠状态无人机无法收集其数据。无人机的飞行轨迹如图3所示。图3中,无人机根据每个传感节点的时间窗制定了数据收集顺序,可以看到,无人机途经传感节点SN4时,由于未在传感节点SN4时间窗内,无人机并未收集其数据,而是直接飞往时间窗较早的传感节点SN1收集数据。此外,可以看到,不同加权因子θ值下的优化轨迹,随着θ的减小,SN的总能耗考虑的权重更大,无人机更靠近每个传感节点进行数据收集以减少传感节点的能耗。 相比之下,θ增加使得无人机的能量消耗更为重要,无人机轨迹的飞行距离减少,能耗降低。 图3 无人机的飞行轨迹Fig.3 Flight path of UAV 当θ=0.2,0.4,0.8时,传感节点的传输调度分别如图4—图6所示,随着加权因子θ增大,加权下的无人机能耗在总能耗中占比随之增大,导致无人机在距离传感节点越远的地方收集数据。由于传感节点的发射功率恒定不变,且满足问题P3中的约束C12,传感节点的数据收集时间也相应增加。反之,当θ较小时,加权下的传感节点能耗在总能耗中占比较少,由(15)式可知传感节点能耗与时间有关,无人机在靠近传感节点的位置收集数据,此时,由于通信信道较好,无人机可以在更短的时间内收集完传感节点的数据。 图4 θ=0.2时传感节点的传输调度Fig.4 Transmission scheduling of sensor nodes when θ=0.2 图5 θ=0.4时传感节点的传输调度Fig.5 Transmission scheduling of sensor nodes when θ=0.4 图6 θ=0.8时传感节点的传输调度Fig.6 Transmission scheduling of sensor nodes when θ=0.8 权值对传感节点能耗的影响如图7所示。随着θ的增大,无人机飞行能耗考虑的权重较大,无人机在距离传感节点较远的地方收集数据,导致传感节点总能耗增加。当θ=0.2时,无人机在距离传感节点较近的位置收集数据,传感节点上传数据的时间减少。由于传感节点以恒定功率上传数据,因此,可降低传感节点总能耗。当θ=0.8时,SN6由于距离较远,无人机为了节省能耗,在较远的地方收集数据,传感节点上传数据的时间变长,导致传感节点的能耗增大。 图7 权值对传感节点能耗的影响Fig.7 Influence of weights on the energy consumption of UAV and sensor nodes 权值对无人机速度的影响如图8所示。无人机在靠近传感节点时降低飞行速度,以较好的通信信道收集数据。此外,加权因子θ增大时,由(14)式可知,无人机降低飞行速度,以实现降低飞行能耗的效果。由于本文设置了时间窗的约束,无人机必须在每个传感节点时间窗内迅速飞到该节点收集数据,因此,优化后的无人机飞行速度变化较大。 图8 权值对无人机速度的影响Fig.8 Effect of weights on the speed of UAV 图9为不同加权因子θ对无人机能耗和所有无线传感节点总能耗的影响,可以看到,随着θ的增大,无人机飞行能耗减小,传感节点总能耗增大。针对传感节点能耗要求较高的场景,传感节点能耗一旦耗尽就会造成能量空洞[18],且无法频繁地充电或者更换电池(例如偏远的山区或者沙漠地区),可以将θ调小适用于该场景。针对无人机飞行能耗要求高的情况下(例如搭载基站服务器的救灾无人机),可以将调高加权因子θ增加无人机的续航时间。 图9 无人机和传感节点能耗的权衡Fig.9 Trade-off of UAV and sensor node energy consumption 为了进一步展示本文方案的性能增益,将5个不同的方案与本文方案对比,分别为最小化无人机飞行能耗、最小化传感节点能耗[7]、TSP方案[19]、最小化数据收集时间方案[20]。图10比较了不同方案下传感节点和无人机的能耗。图10中,最小化无人机飞行能耗为θ=1的极端情况;最小化传感节点总能耗为θ=0的极端情况;TSP方案未对无人机飞行能耗进行优化;最小化数据收集时间虽然可以减少数据收集任务完成的时间,但是造成较高的无人机飞行能耗和传感节点能耗;最大化吞吐量方案导致了无人机飞行能耗和传感节点能耗较高。 图10 比较不同方案下传感节点和无人机的能耗Fig.10 Comparing the energy consumption of sensor nodes and UAV under different schemes 本文在确保无人机在各个节点活跃期内完成数据收集任务的前提下,通过优化传输调度和无人机轨迹来最小化无人机飞行能耗与无线传感节点总能耗的加权和,并进一步探索了无人机飞行能耗和传感节点总能耗之间的基本权衡。由于该问题是混合整数非凸优化问题,很难直接求解。本文先将整数变量松弛为连续变量,并引入2个松弛变量将原问题转化为凸优化问题,最后用CVX求解凸问题。并且,提出了一种基于SCA的高效迭代算法,保证收敛到KKT解。在实际应用中,可以根据系统需求,灵活调节加权因子,在无线传感器网络的寿命和无人机续航能力之间取得良好的平衡。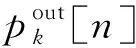

1.3 能耗模型
2 问题描述


3 解决方案
3.1 传输调度参数连续化
3.2 连续非凸问题转化为凸问题





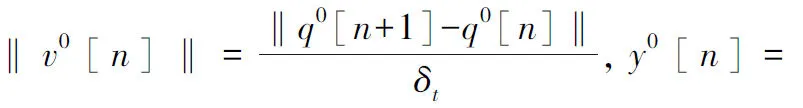

4 仿真结果与分析
4.1 参数设置
4.2 仿真分析





5 结束语
