车联网中面向依赖任务的联合计算卸载及资源分配算法

林 峰,李 华,罗铖文,朱智勤

(1.重庆邮电大学 通信与信息工程学院,重庆 400065;2.重庆邮电大学 自动化学院,重庆 400065)

0 引 言

随着车联网的飞速发展,涌现了各种对延迟敏感的车载应用,例如自动驾驶、自动导航、自然语言处理等应用[1]。但是,现有计算资源和能耗受限的车辆无法充分满足这些应用对低延迟的要求。文献[2]考虑了单移动边缘计算(mobile edge computing,MEC)服务器多个用户的情况,将任务卸载到MEC或者本地计算,以时延和能耗加权和最小化为目标,提出了一种二等分搜索方法来获得最优的卸载决策。文献[3]提出了一种基于粒子群优化算法(particle swarm optimization,PSO)的计算卸载策略,将计算任务卸载到本地和MEC进行计算,平衡了时延与能耗,同时考虑了MEC服务器的负载均衡。文献[4]使用MEC服务器+云端云服务器+本地的联合卸载方式,提出了一种基于强化学习的无模型方法,考虑在能耗和任务的依赖关系约束下,最小化时延。文献[5]考虑任务依赖的迁移方案,并使用基于改进遗传算法(genetic algorithm,GA)求解卸载决策,以最小化时延与能耗的加权和为目标,将计算任务卸载到本地、MEC服务器、远端云进行计算。文献[6]以优化时延和能耗为目标,将多个用户的计算任务卸载到多个MEC服务器,并且考虑计算任务之间依赖关系,基于改进的遗传算法提出了一种联合卸载决策与任务调度算法。

现有研究较少关注依赖任务计算卸载与资源分配问题,且存在依赖任务模型覆盖不全面、远端云服务器的计算卸载延迟大的限制;在考虑任务依赖关系时,大多考虑单个移动设备的依赖任务,并没有考虑多个车辆的依赖任务并发卸载,这与实际应用具有很大的差别。少有研究将卸载决策、资源分配、MEC服务器的负载均综合考虑,并且现有的计算资源也没有得到充分的利用。因此,本文提出了面向依赖任务的联合计算卸载及资源分配算法。首先,该算法考虑多个车辆的依赖任务同时卸载到多个计算平台(车辆本地+MEC服务器+空闲协助车辆+远端云服务器),建立各个计算平台的时延与能耗模型;其次,基于拍卖算法的竞价思想,建立计算资源、通信资源的分配模型,根据负载状态,建立MEC服务器集群的负载均衡度模型;然后,构造联合优化卸载决策、资源分配、负载均衡度的优化问题;最后,结合粒子群算法收敛快与遗传算法全局搜索强的特点,加入爬山搜索策略提高局部搜索能力,提出了自适应粒子群遗传混合算法对优化问题求解。仿真结果表明,与其他算法对比,该算法具有良好的收敛性,能够在满足最大容忍时延的同时,降低系统总开销,有效提升边缘服务器集群的负载均衡度。

1 系统模型

1.1 网络拓扑模型

本文的系统模型如图1所示。本文考虑将MEC服务器部署在路侧单元(road side unit,RSU)上,不失一般性,定义在基站(base station,BS)的覆盖范围内提供计算卸载服务的MEC服务器集合为M={m1,m2,…,mn,…,mm},需要进行计算任务卸载的车辆集合为V={v1,v2,…,vi,…,vk},并且每个车辆都有一个计算密集型任务Si需要卸载,计算密集型任务集合为S={s1,s2,…,si,…,sk}。其中si是可拆分型任务,包含若干个具有时序和数据双重依赖关系的子任务。假设每个卸载车辆所在MEC服务器下都有一些空闲协助车辆提供计算卸载[7],每个MEC服务器mn拥有独立的计算资源Fn和存储资源Wn。本文在BS处设立调度服务器(dispatch server, DS),其作用是对BS覆盖下的所有卸载车辆做统一的卸载决策、管理、协调其范围内所有MEC服务器的资源分配,以及BS的带宽资源分配。计算卸载决策过程视为半动态的,在一个调度周期Δt内即几百毫秒内,车辆集合V和计算密集型任务集合S保持不变,但是在不同的调度周期内集合V,S可能变化[8]。为了减少协同处理时延,RSU与RSU、RSU与BS、BS与远端云服务器之间使用光纤链路连接。车辆与车辆、车辆与RSU之间使用PC5通信,车辆与BS之间使用蜂窝网通信。

图1 系统模型Fig.1 System model

图2 依赖任务模型Fig.2 Dependent task model

本文将卸载车辆vi的计算密集型任务Si的每个子任务建模为十元组S(i,j)={j,I(i,j),O(i,j),U(i,j),Z(i,j),L(i,j),Y(i,j),K(i,j),Q(i,j),E(i,j)}。其中,j表示子任务的编号;I(i,j)表示子任务S(i,j)的数据量;O(i,j)=α·I(i,j)为输出结果数据量,δ为输出数据量系数,表示输出数据量与输入数据量之间的关系;U(i,j)∈{0,1,2,3}表示子任务S(i,j)将要卸载的位置,0表示本地、1表示MEC服务器、2表示空闲协助车辆、3表示远端云服务器;Z(i,j)表示当U(i,j)=1时所对应的MEC服务器的编号,其他情况Z(i,j)=0;L(i,j)表示子任务S(i,j)从卸载车辆vi到计算位置U(i,j)的传输时延;Y(i,j)表示子任务S(i,j)在计算位置U(i,j)的计算时延与计算结果O(i,j)传到下一个计算位置集合K(i,j)的时延;K(i,j)表示S(i,j)后驱子任务的计算位置的集合。

1.2 数据传输模型

(1)

(2)

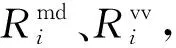
(3)

2 基于双重依赖任务的计算模型

2.1 本地计算模型

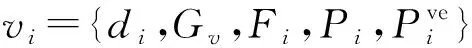
子任务S(i,j)卸载至本地执行传输时延为

L(i,j)=0

(4)

子任务S(i,j)卸载至本地的计算时延为

(5)

为了后续表达式简洁,令

(6)

ξ(i,j,σ)=min(δ(k(i,j)-σ),1),σ=0,1,2,3;

(7)

(8)

(7)式中,δ(t)是冲激函数。

本文考虑车辆是并行的,可以同时与空闲车辆、MEC服务器和BS通信,MEC服务器以及BS也可以并行通信。因此子任务S(i,j)的计算结果O(i,j)从本地车辆传输到后驱子任务计算位置集合K(i,j)的时延应该取最大时延,即为

(9)

(10)

(11)

子任务S(i,j)在本地计算的计算时延与计算结果O(i,j)传到后驱子任务计算位置集合K(i,j)的时延为

(12)

子任务S(i,j)卸载至本地计算的总能耗计算式为

(13)

(14)

2.2 MEC服务器计算模型

子任务S(i.j)从卸载车辆vi到mn服务器的传输通信时延计算式为

(15)

子任务S(i,j)在mn服务器的计算时延为

(16)

(16)式中,F(n,i)表示mn服务器分配给车辆vi的计算资源,单位为cycles/s。

子任务S(i,j)的计算结果O(i,j)从mn服务器传输到后驱子任务计算位置集合K(i,j)的时延为

(17)

(18)

子任务S(i,j)在mn服务器的计算时延与计算结果O(i,j)传到后驱子任务计算位置集合K(i,j)的时延为

(19)

子任务S(i,j)卸载至mn服务器的总能耗计算式为

min(|δ(k(i,j)-1)·(q(i,j)-Z(i,j))|,1)·

(20)

(21)

2.3 空闲协助车辆计算模型

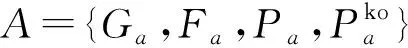
子任务S(i,j)从卸载车辆vi到空闲协助车辆的传输通信时延为

(22)

子任务S(i,j)在空闲协助车辆的计算时延为

(23)

子任务S(i,j)的计算结果O(i,j)从空闲协助车辆传输到后驱子任务计算位置集合K(i,j)的时延为

(24)

子任务S(i,j)在空闲协助车辆的计算时延与计算结果O(i,j)传回到后驱子任务计算位置集合K(i,j)的时延为

(25)

子任务S(i,j)卸载至空闲协助车辆的总能耗计算式为

(26)

(27)

2.4 远端云服务器计算模型

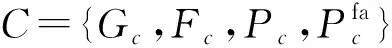
子任务S(i,j)从卸载车辆vi到远端云服务器的传输通信时延为

(28)

子任务S(i,j)在远端云服务器的计算时延为

(29)

子任务S(i,j)的计算结果O(i,j)从远端云服务器传输到后驱任务计算位置集合K(i,j)的时延为

(30)

子任务S(i,j)在远端云服务器的计算时延与计算结果O(i,j)传回到后驱任务计算位置集合K(i,j)的时延为

(31)

(32)

(33)

3 系统总开销模型

本文是分布式的联合计算任务卸载,并且子任务之间具有时序与数据的双重依赖。在本研究中假设车辆是并发的卸载方式,总的时延不是简单的各个子任务时延相加。因此,在考虑任务Si的总时延时,本文采用了关键路径法(critical path method,CPM)[12],在本文中关键路径就是时延最长的路径,所有的路径通过DAG图的广度优先遍历算法获得。

假设车辆vi的任务Si的路径集合为Pi={P(i,1),P(i,2),P(i,3),…,P(i,ρ)},总共有ρ个路径。车辆vi的任务Si路径P(i,ρ)的总时延为

(34)

因为所有不在本地计算的任务都需要卸载出去,所以这部分时延应取传输到MEC、空闲协助车辆、以及远端云服务器中最大的一个时延。而且任务之间具有依赖性,必须等前驱子任务执行完并且把计算结果,传到下一个子任务时才能开始执行,所以在路径p(i,ρ)上计算时延以及回传时延应该是相加。

车辆vi的任务Si的卸载总时延为Ti,总能耗为Ei,计算式为

Ti=max(T(i,1),T(i,2),T(i,3),…,T(i,ρ))

(35)

(36)

车辆集合V的所有计算密集型任务集合S的时延和,即系统总时延为T,总能耗为E,计算式为

(37)

(38)

系统总开销为

H=βT+(1-β)E

(39)

(39)式中,β∈(0,1),为时延权重系数;(1-β)为能耗权重系数。可根据计算密集型任务的需求及车辆车载设备的状态来设置β。例如,当运行时延敏感型的计算服务时,可以适当增加β的值。本文取β=0.8。

4 服务器资源分配与负载均衡模型

4.1 MEC服务器资源分配模型

调度服务器根据每个车辆卸载到各个MEC服务器的计算任务量,以及远端云服务器卸载量的情况,借鉴拍卖算法的竞价思想,将计算资源、BS的带宽资源分配给各个卸载车辆[13]。

车辆vi的任务Si对于mn服务器的计算资源竞价为F(bn,i),mn服务器分配给车辆vi的计算资源为

(40)

(40)式中,a1表示计算资源请求量权值,a1=0.75;a2表示车辆的优先级权值,a2=0.25。当车辆vi处于mn服务器时,其优先级会更高,这样可以减少计算结果的回传时延。

卸载到远端云服务器子任务越多的车辆应该分到更多的带宽资源,这样可以减小传输通信时延,以及结果回传时延。

车辆vi的任务Si对于mn服务器的存储资源分配为

(41)

任务Si所有卸载到mn服务器的子任务必须先存储,并且子任务的计算结果也需要存储才能传给后驱子任务。

4.2 MEC服务器负载均衡模型

在车联网环境中,车辆的移动性造成MEC服务器下卸载车辆分布不均、MEC服务器的负载不均衡,不仅使得资源得不到充分的利用,也导致较差的QoE。所以在进行卸载决策和资源分配时,考虑MEC服务器的负载均衡非常必要。

(42)

因此,mn服务器的负载为

(43)

(43)式中,α1+α2=1;α1表示对计算资源使用情况的重视程度;α2表示对内存资源使用情况的重视程度。本研究对于计算资源与存储资源的重视程度一样,故α1=α2=0.5。

调度服务器下,MEC服务器集合为M={m1,m2,…,mn,…,mm},那么MEC服务器集群的负载集合为GM={G1,G2,…,Gn,…,Gm}。

MEC服务器集群的平均负载为

(44)

本文使用MEC服务器集群负载的标准差ω来表示集群的负载均衡度,表示为

(45)

ω越小,说明MEC服务器集群的负载均衡度越高;ω越大,说明MEC服务器集群的负载均衡度越低。

5 问题建模

在满足每个车辆的计算密集型任务Si的依赖关系以及最大容忍时延和资源限制前提下,以最小化联合卸载系统的总开销和负载均衡度为目标,将系统的任务卸载和资源分配建模为

∀i∈[1,k],∀n∈[1,m]

∀i∈[1,k]

O(i,j))]≤Wn,∀n∈[1,m]

C6:U(i,j)∈{0,1,2,3},

Z(i,j),Q(i,j)∈{1,2,…,m},

K(i,j)∈{0,1,2,3},∀i∈[1,k],

∀j∈[1,xi]

(46)

(46)式中,μ表示系统的总开销在目标函数的权重,(1-μ)表示负载均衡度在目标函数中的权重,如果系统倾向于系统开销,可以增大μ值,相反,如果更看重MEC服务器集群的负载均衡度,可以减小μ值;K=[K1,K2,…,Ki,…,Kk]T为所有车辆的依赖任务的拓扑排序矩阵,K中的第i行对应车辆vi的计算任务Si的拓扑排序向量Ki。

6 算法设计

6.1 粒子和遗传种群初始化

由目标函数可知需要求解K、U、Z、F、W、B等6个矩阵。本文改进PSO算法和GA算法的编码方式,采用多矩阵编码方式,编码示意图如图3所示。粒子种群、遗传种群分别由矩阵运算K·Z、U·Z、Z·Z、F·Z、W·Z、B·Z形成6个大的矩阵构成。以N为种群大小,k为车辆数目,那么要获得第i个粒子/染色体的编码,只需要取出各个矩阵的对应的(i-1)·k+1到i·k行,相关的操作也只需要操作对应的行即可。

拓扑排序矩阵K·Z初始化是从车辆任务的所有拓扑排序中随机选择一种,计算卸载决策矩阵U和MEC编号矩阵Z初始化取(0,1]的随机数,再映射为整数,当MEC服务器的数量n=3时的映射关系为

(47)

整个进化过程主要针对计算卸载决策矩阵U和MEC编号矩阵Z,因为在确定了卸载决策之后,才能根据卸载结果优化卸载的MEC服务器,进行资源分配,使得MEC服务器负载均衡。

6.2 构造适应度函数

上述优化模型是带约束的最小化系统开销和负载均衡度的模型,当采用粒子群遗传混合算法对其进行优化时,需要将约束问题转化为非约束问题。因此,本文采用自适应惩罚函数对目标函数进行约束处理。在进行约束处理时,目标函数中C1、C6约束在编码时处理,C3、C4、C5在采用竞价分配资源方式时必然满足,所以只需要针对C2约束进行惩罚,故适应度函数为

(48)

(48)式中,Γ取值为1 000,因为负载均衡度很小,所以需要提高它在适应度函数中的占比;c(ρ)为惩罚系数,ρ为可行解的比例;fok为可行解;fsum表示解的总数。ρ与c(ρ)成反比关系,当ρ越大时代表可行解增加,c(ρ)应该减小。c(ρ)=0,表示为没有当前种群可行解;c(ρ)=1时,表示当前种群全为可行解。在刚开始的迭代中,种群中可行解数量较少,此时惩罚系数应较高,以引导搜索进入可行域。随着种群的进化,种群中的可行解增多,惩罚系数则应减小[14]。

6.3 粒子群算法和遗传算法相关操作

6.3.1 粒子速度与位置更新

惯性权重较大使得粒子有较好的全局搜索能力,较小则有利于局部搜索。固定的惯性权重会陷入局部寻优,自适应的惯性权重可以使粒子向最优位置移动[15],自适应惯性权重为

(49)

粒子的速度和位置更新公式为

vi(t)=wt·vi(t)+c1·rand[pi(t)-xi(t)]+

c2·rand[pg(t)-xi(t)]

xi(t+1)=xi(t)+vi(t)

(50)

(50)式中,c1、c2为学习因子;pi(t)、pg(t)分别为个体历史最优位置和种群全局最优位置。

6.3.2 选择交叉与变异操作

在GA算法中,交叉概率过小,在迭代过程中会影响种群的丰富度,导致收敛缓慢;过大则会影响优良个体的遗传。变异概率过小不容易产生新个体,影响种群多样性;过大则会陷入局部最优[17]。因此,本文采用自适应的交叉概率和变异概率。种群的适应度值较分散,说明种群比较丰富,交叉概率和变异概率应该减小;反之,种群的适应度值较集中,说明种群的丰富度不够,交叉概率和变异概率应该增大[18]。

自适应交叉概率表示为

(51)

自适应变异概率表示为

(52)

(51)—(52)式中,favg为当前种群平均适应度;fmax为当前种群的最大适应度;k1、k2为(0,1]的常数。

选择和交叉操作采用单点部分映射交叉(partial-mapped crossover,PMX)与君主方案相结合的方式[19]。首先,对种群根据适应度值进行升序排列,用最优的个体与所有偶数位置个体进行交叉,每次交叉之后产生两个新的个体;其次,对交叉后新产生的个体进行变异操作产生子群体;然后,计算其适应度值;最后,和父群体合并,并且根据适应度值进行升序排列,取前N个体为新的群体,进行下一步的操作。

7 仿真实验与结果分析

7.1 仿真参数设置

为了验证本文算法的有效性,通过实验与其他算法进行对比,实验仿真参数如表1[20]和表2所示

表1 PSO与GA算法相关参数Tab.1 PSO and GA algorithm related parameters

表2 仿真参数Tab.2 Simulation parameters

7.2 仿真结果分析

在本节中分别对Random算法、PSAO算法[3]、JODTS算法[6]、本文算法进行仿真和对比。Random算法将依赖任务随机卸载到本地、MEC服务器、空闲车辆、远端云服务器进行计算。PSAO算法基于改进的粒子群算法的卸载策略,将计算任务卸载到本地、MEC服务器进行计算。JODTS算法基于改进遗传算法的卸载策略,将计算任务卸载到本地、MEC服务器进行计算。

图4展示了不同算法的收敛性能。图4中k=8,n=3,计算任务量为4 Mbit。从图4可以看到,本文算法收敛速度最快,大概迭代120次时收敛。PSAO的收敛度居中,大概迭代140多次时收敛。收敛最慢的是JODTS算法,大概迭代210多次时收敛;在全局寻优上本文算法最好,其次是JODTS算法,最差的是PSAO算法。因为粒子群算法单向传递信息,而遗传算法是双向的,所以粒子群算法收敛比遗传算法快,但是它容易陷入局部最优,因此其寻优能力没有遗传算法强。本文算法结合两个算法的优点,并加入爬山搜索策略进行局部二次搜索,使得全局寻优能力、收敛性能都有所提高。

图4 算法收敛性分析Fig.4 Convergence analysis of the algorithm

图5展示了当DS下车辆数和MEC服务器数量一定时,计算任务量对系统总开销的影响。图5中,k=8,n=3。从图5可以看出,随着计算任务量的增加,4种算法的系统总开销也随着增加;本文所提算法的系统总开销最低,约是Random算法的49.15%、PSAO算法的68.10%、JODTS算法的87.62%。当计算任务量超过12时,系统总开销增幅明显增大,这是因为计算任务量过大造成数据传输和回传开销,MEC的计算开销也明显加大。从图5中还可以看到,采用本文算法时,平均每辆车的时延小于计算任务的最大时延,这说明本文算法能够在满足最大容忍时延的同时,最小化系统总开销。

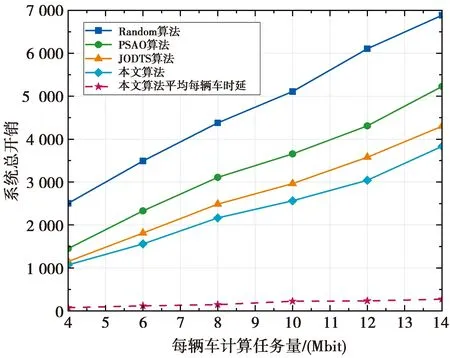
图5 计算任务量对系统总开销的影响Fig.5 Calculate the impact of task volume on total system overhead

图6展示了在MEC服务器数量、计算任务量和在子任务个数一定的情况下,车辆数对负载均衡度的影响。图6中,n=3,车辆计算任务量为6 Mbit,子任务数为10。从图6可以看出,本文所提算法相比其他3种算法具有最小的负载均衡度,并且负载均衡度增幅是最小的,能有效均衡DS下MEC服务器的负载。

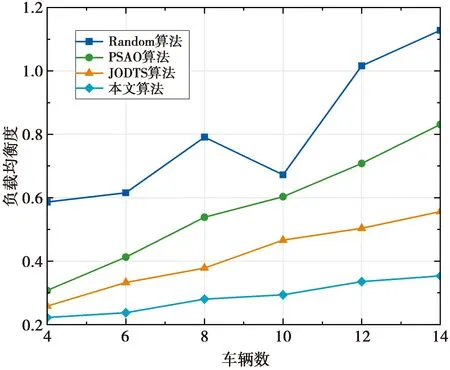
图6 车辆数对MEC服务器负载均衡度的影响Fig.6 Impact of the number of vehicles on MEC server load balancing

图7展示了车辆数对MEC服务器负载均衡度的影响。图7中,k=8,n=3,车辆计算任务量为6 Mbit。从图7可见,车辆个数、MEC服务器数和计算任务量一定时,系统总开销随着输出数据量系数δ的增加而增加;对比其他3种算法,本文算法具有最小的系统总开销且输出数据量对系统总开销的影响较小,这是因为输出数据量比较小,而且本文中在MEC服务器之间、MEC与BS之间、BS与远端云服务器之间使用的是光纤,带宽很大。

图7 输出数据量对系统总开销的影响Fig.7 Impact of output data volume on total system overhead

8 结束语

为了解决子任务之间的时序和数据双重依赖关系导致的依赖时延问题、车辆的移动性分布不均造成MEC服务器的负载不均衡问题,以及降低时延与能耗,本文提出了一种基于双重依赖任务的联合计算卸载及资源分配算法。本文考虑了多个车辆的依赖任务同时卸载到多个计算平台的情况,提出了自适应粒子群遗传混合算法联合优化卸载决策、资源分配、负载均衡度。仿真实验表明,本文算法能够在满足最大时延的同时,降低系统总开销,提升边缘服务器集群的负载均衡度。