多波束卫星通信系统的能效优化功率分配算法

向碧群,江 源,夏永红

(1.重庆移通学院 公共大数据安全技术重点实验室,重庆 401420;2.重庆邮电大学 通信与信息工程学院,重庆 400065)

0 引 言

随着多波束卫星通信的不断发展,利用资源分配技术,多波束卫星通信系统可以满足日益增长的通信需求,然而高数据速率和服务质量快速增长的同时还带来了系统能耗的急剧增加。由于卫星通信系统的能源成本较大,且一味追求高速率带来的碳排放污染,不符合当今倡导的绿色低碳环保理念。另外,提高系统能效可以有效延长卫星使用寿命和减小卫星尺寸。因此,能效作为一种衡量系统性能的重要指标,在学术界和工业界都引起了广泛关注。而博弈论作为一种有效的资源分配方式,能够很好地协调卫星和用户之间的资源需求,动态地调整资源分配决策。

文献[1]提出集中式能量效率(energy efficiency,EE)最大化功率分配问题,通过分布式博弈论功率控制算法得到最优解,在保证最小服务质量(quality of service,QoS)的前提下,降低了计算复杂度。文献[2]针对多波束卫星通信中总功率和QoS约束下能效最大化问题,分别提出基于迫零(zero forcing,ZF)和连续凸逼近(successive convex approximation,SCA)的预编码设计算法,数值结果表明,基于SCA的预编码算法优于基于ZF的预编码算法。文献[3]以最大化多播多波束卫星通信系统中EE为目标,需考虑总功率和QoS约束下的预编码设计问题。仿真结果显示,该文献所提算法能够在多播场景的卫星通信中提高系统能效。上述研究虽然在一定程度上提高了系统能效,但针对多波束卫星通信系统的能效优化问题仍需进一步研究。

基于上述分析,在用户分组结果下,本文提出了基于斯坦克尔伯格博弈的能效优化功率分配算法,旨在满足用户最小QoS的前提下,提高多波束卫星通信系统的能效。采用斯坦克尔伯格博弈模型,用户作为买方,卫星作为卖方,在考虑相关约束条件下,分别构建自身效用函数,通过寻找最优功率分配策略来最大化自身效用函数,最终达到斯坦克尔伯格博弈均衡。其中,用户方由于自身效用函数非凸,故首先利用Dinkelbach算法将非凸的分式规划问题转化为等效减数形式的凸函数;然后通过拉格朗日数乘法求得最优功率值;最后通过仿真实验验证所提算法的有效性。

1 系统模型

本文研究的多波束卫星系统结构如图1所示。在GEO多波束卫星系统前向链路,其中一个单宽带多波束卫星为Ktotal个用户提供服务,且采用全频率复用方式来提高频谱效率。假设Ktotal个用户均匀分布在卫星产生的N个波束内,平均每个波束服务⎣Ktotal/N」个用户。为同时服务多个用户,多波束卫星同时采用时分多址技术(time division multiples,TDMA)和非正交多址接入(non-orthogonal multipleaccess,NOMA)技术。系统通过TDMA技术以帧为单位同时为多个用户提供服务,每帧包括T个时隙,同时每个时隙下每个波束通过NOMA技术选择一个用户簇进行数据传输,每簇内有B个用户。

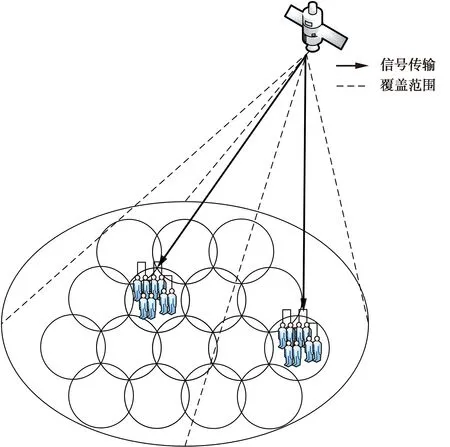
图1 多波束卫星通信系统模型图Fig.1 Model diagram of multi-beam satellite communication system

yGt=HGtx+n

(1)

(1)式中:HGt∈Kt×N是t时隙下卫星和用户组Gt之间的信道矩阵;x∈N是t时隙下卫星的传输信号,Kt×1表示均值为0、方差为的加性高斯白噪声。

(2)

(3)

(4)

(5)

所以,整个多波束卫星通信系统的能效ηtotal为Ktotal个用户能效的累加和的平均,可表示为

(6)

2 基于斯坦克尔伯格博弈的能效优化迭代功率分配算法

假设对多用户进行分组,得到分组结果Gt。基于该分组结果,在卫星功率资源有限的情况下,多用户之间资源竞争为最大化用户能效所致。考虑到卫星和用户之间的功率交易问题。卫星可向用户出售功率资源,用户通过从卫星购买功率资源满足自身所需。根据卫星和用户之间的关系,构建斯坦克尔伯格博弈模型,将卫星作为功率资源的拥有者,在模型中充当卖方,卫星将功率以合适的定价出售给用户,从而获得自身收益最大化;而用户作为功率资源的竞争者,在模型中作为买方,根据卫星出售的功率价格适当买入使自身效益最大化。根据买卖结果不断调整博弈,最终达到斯坦克尔伯格均衡,双方均取得最大化自身效益。

博弈三要素主要体现如下。

1)博弈者。构建的多波束卫星通信系统中,单个卫星和卫星服务范围内的所有用户充当模型中的博弈者。

2)决策集。卫星根据用户决策不断调整的功率价格高低以及用户每次对卫星功率的购买数量多少都属于决策集。

3)效益。用户每次购买功率后获得的能效收益,卫星卖出功率后的经济收益都属于博弈过程中的效益。

2.1 问题建模及分析

本文的优化目标是在多波束卫星通信系统中,基于用户分组结果,通过不同用户组的用户功率分配问题来最大化用户服务公平性及系统能效。基于用户分组结果,最大化系统能效问题可视为每个时隙下用户组能效最大化。故多波束卫星通信系统的能效优化问题可以等价为T个最大化能效的功率分配子问题求解。将用户作为买方,卫星作为卖方,构建斯坦克尔伯格博弈模型,两者之间通过买卖交易来实现自身效用函数最大化。

2.1.1 买方(用户)最大化效用函数问题

(7)

2.1.2 卖方(卫星)最大化效用函数问题

(8)

2.2 非凸问题转换

观察发现目标函数(7)式并不是标准的分数形式,无法直接转化为凸函数,故先将其通分,转化为分数形式,如(9)式。

(9)

(10)

Dinkelbach算法首先将计算复杂度较高的分式问题转换为易于求解的减法形式的等价问题[7]。引入辅助变量qn,b,有

(11)

经过等效转换得

(12)

(13)

因此,根据上述分析,(7)式可以等效转换为

s.t. C1-C4

(14)

2.3 策略分析

2.3.1 买方策略分析

(15)

(16)

(16)式中,αn,b,βn,b,γn,b分别为非负的拉格朗日算子。

λn,bPc-qn,b-αn,b+βn,b-γn,b=0

(17)

(18)

(18)式中,cn,b=qn,b+αn,b-βn,b+γn,b,且利用梯度法迭代更新拉格朗日算子。

(19)

(20)

(21)

(19)—(21)式中:[·]+=max{0,·};i是迭代次数;ζi表示迭代步长。选择恰当的ζi值,能够保证拉格朗日算子快速收敛到最优值。

2.3.2 卖方策略分析

(22)

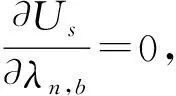
(23)

(24)

2.4 最优解的存在性分析

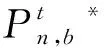
她擦着一根洋火，点亮桌上的罩子灯，屋里映得跟个白昼样儿。吃完饭，赛十娘把碗一推，又叼起根烟。她长长地嘘出一口烟雾，拿腔拿调地说：“饭后一支烟，快活似神仙。”

(25)

(26)

证明

证明:

(27)

由于单位功率价格λn,b大于0,所以分母始终大于0,有

(28)

(28)式的分子可写为

(29)

证明

Us对λn,b求二阶导可得

(30)

2.5 能效优化的迭代功率分配算法

根据上述分析,得到基于斯坦克尔伯格博弈的能效优化功率分配算法,如算法1所示。

算法1基于斯坦克尔伯格博弈的能效优化迭代功率分配

输入:用户组信道矩HGt预编码矩阵W,卫星发射功率P,用户最小传输速率Rmin

1.设置最大内、外层迭代次数Tinner、Touter,内、外层误差容忍门限值κ、δ

4.forn=1:Ndo

5.forb=1:Bdo

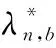
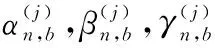
10.j=j+1

11.end while

12.end for

13.end for

15.i=i+1

16.end while

2.6 算法复杂度分析

3 仿真分析

通过MATLAB仿真软件对所提基于斯坦克尔伯格博弈的能效优化迭代功率分配算法性能进行仿真验证。为验证本章所提算法的有效性,分别和文献[3]所提算法及文献[10]所提算法进行对比分析。

3.1 仿真参数设置

仿真场景为单颗配备N个波束的多波束GEO卫星,多个波束的覆盖范围构成整个卫星的覆盖面积,且每个波束在单个时隙下采用PD-NOMA技术同时服务2个用户。其余仿真参数如表1所示。

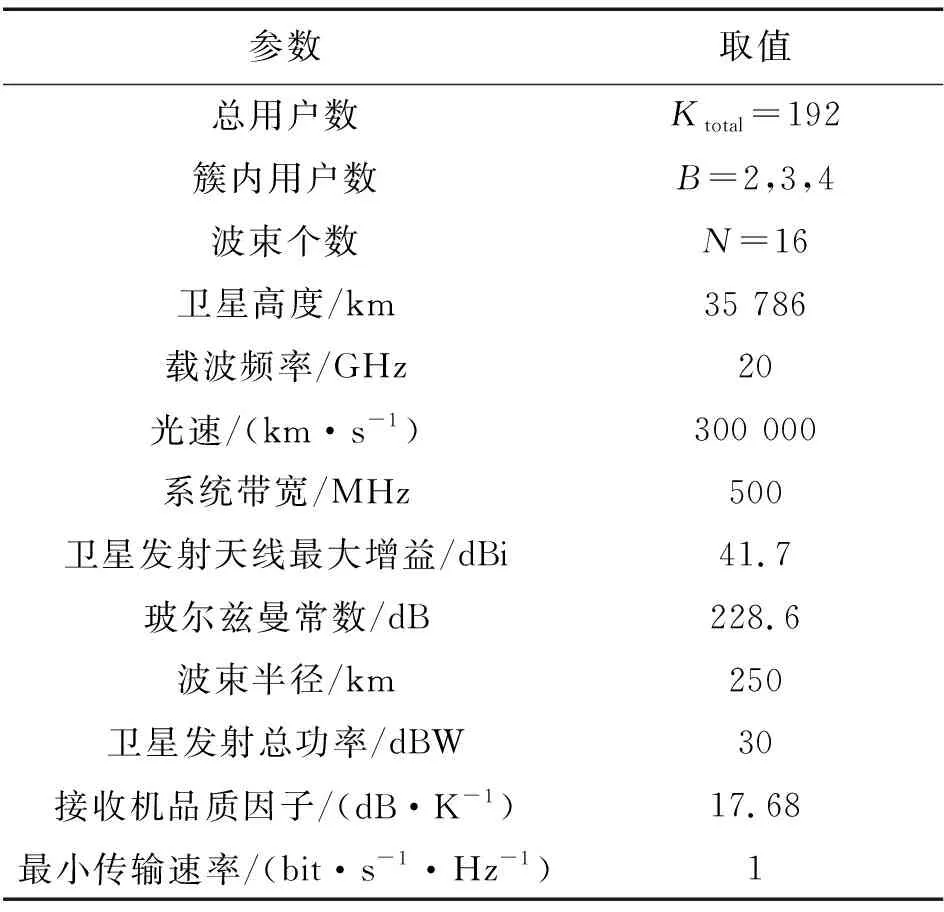
表1 仿真参数表Tab.1 Simulation parameter table

3.2 仿真结果分析

图2描述了所提算法中用户购买功率值大小的迭代收敛过程。在用户分组情况下,假设簇内用户数B=3,卫星发射功率为27 dBW,卫星电路固定消耗功率为10 W。为方便观察所提算法的变化趋势,图2中仅展示第一个用户组中,第一个波束内3个用户购买功率值大小的收敛情况。从图2可知,所提算法的用户购买功率在第4次迭代后收敛,最终收敛值即表示用户在卫星处购买的功率大小。从图2可以看出,用户1购买的功率最少,其次是用户2,用户3购买的功率最多,这符合所提算法中信道条件与所得功率成反比的预设。

图2 基于能效优化的功率迭代收敛过程Fig.2 Power iterative convergence process based on energy efficiency optimization

图3描述了所提算法中,卫星设置的单位功率价格的迭代收敛过程。其仿真条件与图2的条件相同。图3中,簇内每个用户基本经过4次迭代后,卫星的单位功率价格达到收敛状态,此时用户和卫星之间的博弈达到均衡,无论卫星和用户再做任何改变,收益都不会再增加。且从图3可知,信道条件越差的用户购买卫星功率的单位价格越低,即用户3的价格最低,其次是用户2,用户1的价格最高。因此,用户3能够以较低的价格买到更多的功率,从而提高自身的传输速率来满足本章所提算法最小QoS的约束条件。

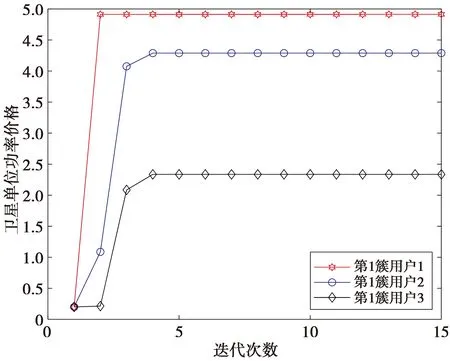
图3 基于能效优化的价格迭代收敛过程Fig.3 Iterative price convergence process based on energy efficiency optimization

图4研究了所提算法在簇内不同用户数下卫星电路固定消耗功率与系统能效的关系。仿真中给定卫星发射功率为27 dBW。由图4可知,随着卫星电路固定消耗功率的增加,系统能效逐渐减小。这是由于卫星电路固定消耗功率的增加,卫星总功率用来分给用户的功率值就会减少,从而单个用户的传输速率降低,导致系统能效降低。另外,在相同卫星固定消耗功率下,所提算法的系统能效随簇内用户数的减少而增加。这是由于在克服卫星电路固定消耗功率后,有限的卫星功率资源分配给的用户越多,在满足每个用户最小传输速率要求后,强用户得到的功率越少,用户传输速率变低,从而系统能效减小。

图4 不同卫星电路固定消耗功率下系统能效比较Fig.4 Comparison of system energy efficiency under fixed power consumption of different satellite circuits

图5比较了所提算法在簇内不同用户数下卫星发射功率与系统能效的关系。仿真中给定卫星电路固定消耗功率为10 W。由图5可知,随着卫星发射功率的增大,所提算法的系统能效会先快速增加然后保持基本稳定。且随簇内用户数的增加,其系统能效逐渐降低。由于簇内用户数增大,使得有限功率内分给每个用户的功率减少,从而单个用户的传输速率降低,系统能效也随之减小。

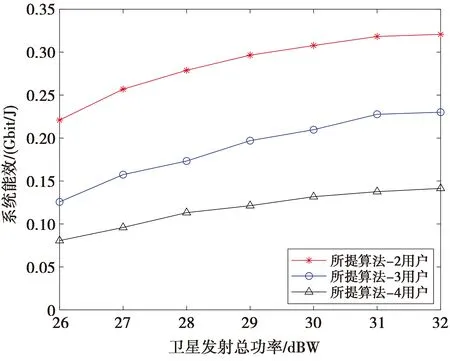
图5 不同卫星发射功率下系统能效比较Fig.5 Comparison of system energy efficiency under different satellite launch powers

图6研究了不同算法在卫星发射功率下的系统能效变化趋势。仿真中给定卫星电路固定消耗功率为10 W,本章所提算法的簇内用户数B=2。从图6可以看出,卫星发射功率从26 dBW开始,3种算法的能效都在单调递增,本章所提算法在卫星发射总功率30 dBW之后趋于平缓,文献[3]所提算法在卫星发射功率27 dBW后保持稳定,文献[10]所提算法在卫星发射功率28 dBW后不再变化,意味着增加卫星发射功率可以适当提高系统能效。且从图中可以看出,所提算法的系统能效始终高于文献[3]和文献[10]的系统能效。

图6 卫星发射功率下不同算法的系统能效比较Fig.6 System energy efficiency comparison of different algorithms under satellite launch power

4 结束语

本文主要研究在多波束卫星通信系统中,基于用户分组的情况下,建立能效优化的功率分配模型。将用户和卫星分别设为买方和卖方,构建斯坦克尔伯格博弈模型,卫星根据用户购买的功率量设置不同的单位价格,用户根据卫星设置的单位功率价格适当买入,双方分别最大化自身效用函数。由于用户效用函数是分式的非凸问题,故首先将非凸的分式问题利用Dinkelbach算法转换为减数形式的凸问题,然后利用拉格朗日数乘法对问题求解。仿真结果表明,本文所提算法具有较好的能效性。