网络环境下非线性切换系统的固定时间控制

马加立,费树岷 ,崔国增

(1.东南大学自动化学院,江苏南京 210096;2.苏州科技大学电子与信息工程学院,江苏苏州 215009)

1 引言

作为一类特殊的混杂系统,非线性切换系统广泛存在于各类实际工程应用中,例如电力系统、化工系统、网络系统等[1].并且相较于单个系统,切换系统的控制问题更加棘手[2].因此,切换系统的控制问题吸引了国内外学者的广泛关注.随着共同Lyapunov函数法、多Lyapunov函数法以及驻留时间法的提出,非线性切换系统的分析和控制得到了长足的发展[3–6],但仍然存在一些棘手问题尚未解决.

一方面,随着计算机与网络通讯技术的迅速发展,网络控制系统因其可靠性高、灵活性高以及便于维护等优点,已经在军事、医疗、航空航天等复杂工业控制领域得到了广泛地应用.然而在网络控制系统中,由于量化技术产生的量化误差往往会增加闭环系统的分析和设计的难度,甚至导致不稳定现象的产生.因此量化控制显得尤为重要.借助于反步设计方法和自适应技术,量化控制已经在各类非线性系统上取得了丰硕的成果,包括严格反馈系统[7]、纯反馈系统[8]、非严格反馈系统[9]以及多智能体系统[10].并且借助共同Lyapunov函数法,非线性切换系统的量化控制问题同样得到了解决[11–13].然而需要指出的是,上述结论往往建立在量化器参数已知的前提下.在实际工程应用中,系统的结构是复杂多变的,量化器参数信息往往不可获得.因此,对于量化器参数未知的网络控制系统的分析和设计还有待研究.

另一方面,现代工业发展对系统的收敛速度要求越来越高,通常要求系统状态在有限时间内收敛,因此上述文献[7–13]所获得的渐近稳定结论已经很难满足控制要求.近年来,有限时间控制因其收敛速度快、跟踪精度高以及抗干扰能力强等优点,吸引了国内外学者的广泛关注和研究,并且已经取得了显著的成果.例如,文献[14]利用增加幂次积分法,解决了严格反馈非线性系统的有限时间量化控制.通过结合增加幂次积分法和共同Lyapunov函数法,严格反馈非线性切换系统[15]、高阶切换系统[16]以及随机切换系统[17]的有限时间控制问题已经得到了解决.除此以外,借助有限时间滤波器,文献[18–19]设计了基于命令滤波器的有限时间控制器,解决了“复杂性爆炸”问题.然而需要指出的是,有限时间控制的收敛时间依赖于初始状态.当初始条件未知时,系统的收敛时间很难获得.上述问题一定程度上限制了有限时间控制的应用.为此,文献[20]提出了改进的有限时间控制方法,即固定时间控制,从而保证收敛时间独立于初始条件.在文献[20]的基础上,文献[21–22]实现了单一非线性系统的固定时间量化控制.另外利用增加幂次积分法和共同Lyapunov函数法,高阶切换系统[23]、随机切换系统[24]以及时滞切换系统[25]的固定时间控制也同样得到了解决.然而现阶段关于切换系统的固定时间量化控制结论还相对较少,并且往往要求系统的量化器参数已知[21–22],保守性较大.另外需要指出的是,上述固定时间控制结论都是建立在系统的控制系数已知的前提下[21–25].当控制系数未知时,系统的固定时间控制问题将变得更加困难.原因在于: 现阶段处理未知控制系数的主要方法是Nussbaum函数法,然而此类方法只能保证闭环系统的渐近稳定性,无法实现固定时间控制[26].如何在控制系数未知的前提下实现非线性系统的固定时间控制仍是控制领域的一大难点.

基于以上分析,本文研究了带有未知控制系数和量化输入的不确定非线性切换系统的固定时间控制问题.利用增加幂次积分法和共同Lyapunov函数法,设计了切换类型的自适应固定时间控制器,并给出了相应的参数切换律,最终保证了闭环系统的固定时间稳定性.本文的主要创新点如下: 1)本文首次研究了不确定切换系统的固定时间量化控制问题.相较于现有文献[21–22]里的单个非线性系统,本文研究了一类结构特性更加复杂的混杂系统;2)与文献[21–22]中的结论相比,本文不要求系统的量化器参数及其上下界已知.通过设计新颖的自适应控制器可以有效补偿未知量化器参数,从而减小了所得结论的保守性;3)不同于文献[21–25],本文允许系统的控制系数及其上下界未知.并且不同于传统的Nussbaum函数方法,本文提出了一类切换类型的自适应控制器来处理未知的控制系数,并基于改进的固定时间控制理论设计了新颖的参数切换律,有效补偿了未知的系统参数,最终实现了闭环系统的固定时间收敛性.

2 问题描述及预备知识

考虑如下不确定非线性切换系统:

其中:x=[x1···xn]T∈Rn表示系统的状态变量;切换信号δ(t):[0,+∞)→Ω={1,2,···,K}表示未知的分段连续函数;K表示子系统数量;对于任意的k∈Ω,bi,k(x,t)表示系统的未知的控制系数;光滑函数fi,k(,θ)满足fi,k(0,θ)=0,其中=[x1···xi]T,θ是未知的系统参数;本文采用如下迟滞量化器建模量化输入q(u)[7]:

其中:ui=σ1-iu0(i=1,2,···),u0>0决定了q(u)的死区范围,0<σ<1表示量化密度的度量,δ=.在本文中量化参数u0和σ是未知的.根据文献[14],量化输入q(u)满足以下关系:

注1在现有文献[11–14,21–22]中,系统的量化器参数u0和σ往往是已知的.然而在实际工程应用中,量化器参数信息有时候不可获得[7].针对此类情况,本文去除了对量化器参数的限制条件,从而减小了系统的保守性.

注2相较于对数量化器,本文采用了迟滞量化器来避免抖振现象.如文献[7]所示,当u发生振荡时,迟滞量化器的量化值q(u)是间接变化,这种间接变化为量化值提供了停留时间,从而避免了抖振现象.

本文的控制目标是设计一类自适应控制器使得系统在任意切换信号作用下状态x都可以在固定时间内收敛到零点.为了实现控制目标,首先给出以下假设条件.

假设1对于任意k∈Ω,存在光滑函数ψi,k()≥0和未知常数θk>0使得系统函数fi,k(,θ)满足

注3假设1是解决非线性系统自适应控制问题的普遍条件[14].并且考虑到fi,k(i,θ)满足fi,k(0,θ)=0,结合文献[28]中引理2.2、引理2.5和泰勒展开式,同样容易得到假设1.在现有关于非线性系统的固定时间控制的结论中[21–25],系统的控制系数bi,k或者其上下界往往要求已知.

注4作为处理未知控制系数的经典方法,Nussbaum函数法只能保证闭环系统的渐近收敛性,无法实现非线性系统的固定时间收敛性.因此在现有的关于非线性系统的固定时间控制文献[21–25]往往要求系统的控制系数或者其上下界已知.在假设2中,本文放宽了控制系数的假设条件,研究了更一般非线性切换系统的固定时间控制问题.本文将设计一类切换类型的控制器实现对未知控制系数的补偿,从而保证闭环系统的固定时间收敛性.

引理2[24]对于任意xi ∈R和实数γ>0,以下不等式成立:

引理3[26]给定常数µ>0,ν>0 以及函数γ(x,y)>0,对于任意实数x和y以下不等式成立:

引理4[27]假定正定函数V(t)满足以下条件:

其中:a>0,0<µ<1,ν>1以及µ+ν=2,则以下结论成立:

3 主要结论

3.1 控制器设计

本节将结合增加幂次积分法和共同Lyapunov函数法设计系统的自适应控制器.首先定义如下参数:

并且引入如下虚拟控制器和坐标变换:

其中s是可调节的控制器参数.

步骤1令.考虑如下共同Lyapunov候补函数:

针对每一个子系统k,由式(1)和式(9)可得V1对时间的导数为

根据假设1可得

将式(13)–(14)代入式(12)可得

步骤i(i=2,···,n-1)选取如下共同Lyapunov候补函数:

针对每一个子系统k,由式(17)可得Vi对时间的导数满足

下面对式(18)右边几项进行估计.首先根据引理1和引理3可得

由假设1及式(9)可得

根据式(20),由引理3可得

其中:δik2≥0为未知常数,ϕi,k2≥0为已知C1函数.

类似的,利用引理1和引理3可以得到

其中:δik3≥0为未知常数,ϕi,k3≥0为已知C1函数.

将式(19)–(22)代入式(18)可得

将式(24)代入式(22)可得

步骤n选取如下共同Lyapunov候补函数:

同步骤i类似,针对每一个子系统k,Vn对时间的导数满足以下不等式:

设计系统的控制输入u为

其中:sgn(·)为符号函数,

将式(29)–(30)代入式(28)得到

3.2 切换律设计

在第3.1节设计了带有可调参数s的控制器,在这一节将设计参数切换算法在线调节控制器参数s,从而实现闭环系统的固定时间稳定.

首先定义如下正定函数:

骤1初始化: 令s=1,t1=0,选取合适的单调递增函数h(s);

步骤2切换条件:对于t>ts,如果

则令ts+1=t,s →s+1.否则ts和s保持不变.跳到步骤3;

步骤3重复步骤2.

注5第3.1 节设计了带有可调参数s的系统控制器.第3.2节基于固定时间稳定性理论,设计了自适应参数切换律,动态调节控制器参数s,从而完成对未知参数bi,δ(t)(x,t)和θ的补偿,实现闭环系统的固定时间收敛性.

4 稳定性分析

定理1考虑不确定非线性切换系统(1),在假设1–2条件下,可以设计自适应控制器(29)和相应的参数切换律使得闭环系统的所有信号都是有界的,并且系统状态x可以固定时间内收敛到零点.

证首先由第3.2节可得,在区间[ts,ts+1)不发生切换,且下式成立:

由式(36)可以看出x在区间[ts,ts+1)上是有界的.假定最后一次切换发生在t时.则对于t≥t,下式同样成立:

即x在[t,+∞)上是有界的.因此x在[0,+∞)都是有界的.

因为ϕj0≥0,且ϕjk≥0,结合假设2和式(38)可得

对于t≥ts∗,将式(39)–(41)代入式(31)可得

利用引理2可得

由式(45)–(46)可知

恒成立.对于t≥ts∗,利用引理4,根据式(47)可以得到

根据式(48)可以看出切换条件(35)不再满足,因此对于t≥ts∗,s不会再发生切换.s:1-→s∗经历了s∗-1次切换,因此s的切换次数是有限的,不存在有限时间内切换无数次的现象.

最后将证明系统状态x可以在固定时间内收敛到零点.一方面,假设存在

显然存在矛盾.因此对于任意的

即x(t)≡0.考虑到x=0是系统的平衡点,可以推出x(ts+1)=0,则s在ts+1时刻不会发生切换,显然矛盾,所以ts+1-ts≤∆s.根据以上结论可以得到系统的收敛时间满足

即闭环系统的固定时间稳定性成立.证毕.

注6不同于现有结论,本文并没有采用Nussbaum函数法处理未知的控制系数.而是利用改进的固定时间控制理论,在第3.2节设计了一类基于状态的参数调节律.并且如第4节所示,所提出的参数调节律有效补偿了未知的系统参数,进而保证了闭环系统的固定时间稳定性.

5 仿真结果与分析

例1考虑如下非线性切换系统:

在仿真实验过程中,系统参数选取如下: 切换信号δ(t):[0,+∞)→Ω={1,2},其响应曲线如图1所示;系统的非线性函数f2,1=x2-x1-0.25,f2,2=-1.5x2|x2|;控制系数b1,1=1,b1,2=1,b2,1=0.25,b2,2=0.25;量化器参数σ=0.2,u0=0.02.

首先,当系统的初始条件为x0=[x1(0)x2(0)]T=[5-5]T时,选取控制参数为:c1=2,c2=2,β0=1.2,分别选取h(s)为h(s)=0.2s和h(s)=0.4s,则仿真结果如图2–4所示,其中图2和3给出了系统状态x的响应曲线,图4刻画了控制器参数s的响应曲线.在不同的控制参数下,系统状态x都可以收敛到零点.结合图2–4可以看出,不同的控制参数h(s)可以改变系统的收敛时间以及s的切换次数.但根据第4节中结论:,由图2–3可以看出收敛时间T0≤T,即固定时间稳定性成立.

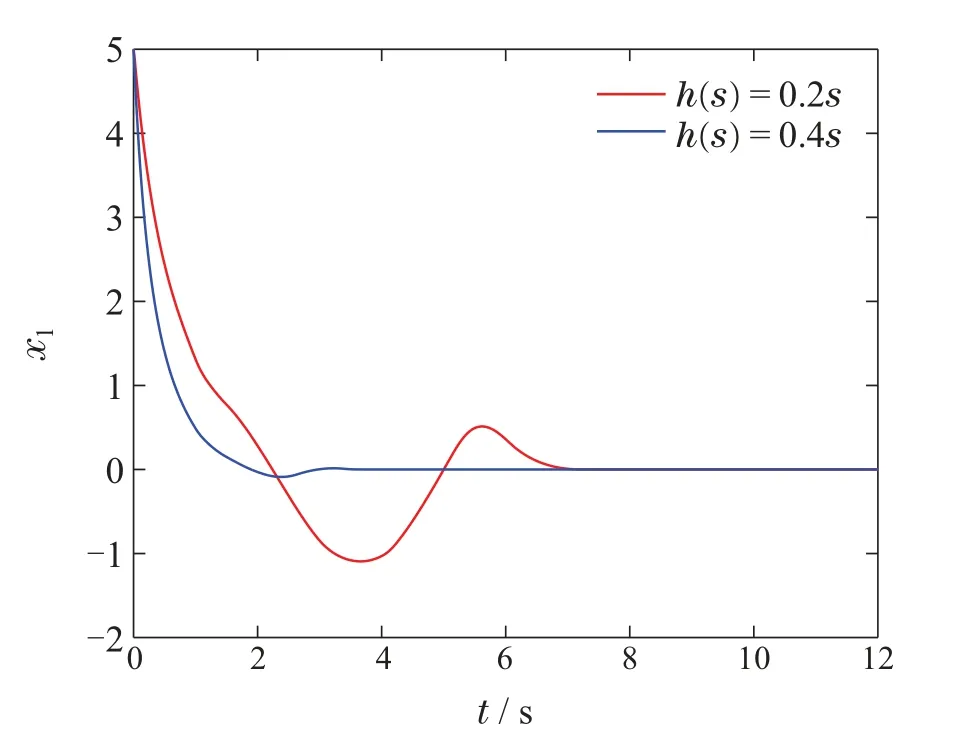
图2 状态变量x1的轨迹Fig.2 Trajectories of x1

图3 状态变量x2的轨迹Fig.3 Trajectories of x2

图4 控制器参数s的轨迹Fig.4 Trajectories of controller parameter s

其次,选取不同的初始条件x0=[x1(0)x2(0)]T=[2-2]T,x0=[x1(0)x2(0)]T=[5-5]T以及x0=[x1(0)x2(0)]T=[6-60]T,在相同的控制器参数c1=2,c2=2,β0=1.2,h(s)=0.4s情况下,系统响应曲线如图5–6所示.由图5–6可以看出,虽然不同初始条件下系统的响应曲线有所差别,但收敛时间几乎相同,并没有随着初始条件的增大而增长,即收敛时间不依赖初始条件,上述仿真结果再一次验证了闭环系统的固定时间稳定性.

图5 状态变量x1的轨迹Fig.5 Trajectories of x1

图6 状态变量x2的轨迹Fig.6 Trajectories of x2

6 结论

本文研究了具有未知控制系数和量化输入信号的不确定非线性切换系统的全局固定时间控制问题.相较于现有结论,本文放宽了对控制系数和量化器参数的假设条件.不同于传统的Nussbaum函数法,本文借助于增加幂次积分法和共同Lyapunov函数,设计了切换类型的自适应控制器.并基于改进的固定时间控制理论,提出了新颖的参数调节律,通过在线调节控制器参数有效补偿了未知的系统参数,从而保证了闭环系统的固定时间稳定性.所提供的仿真实验验证了所提算法的可行性.

需要指出的是本文未考虑外部噪声情况.众所周知,随机非线性系统一直是控制领域的研究热点,其控制问题吸引了国内外学者的广泛关注.因此,未来笔者也将会着重研究非线性随机切换系统的固定时间控制问题.