微晶格穹顶拓扑结构锚杆托板吸能特性研究

2023-10-26杨发旺张庆贺梁志威王明刚

煤矿安全 2023年10期

杨发旺，张庆贺 ,2,3 ，梁志威，王明刚

（1.安徽理工大学土木建筑学院，安徽淮南 232001；2.安徽理工大学深部煤矿采动响应与灾害防控国家重点实验室，安徽淮南 232001；3.合肥综合性国家科学中心能源研究院（安徽省能源实验室），安徽合肥 230031；4.中铁四局集团第五工程有限公司，江西九江 332000）

煤炭作为我国主体能源，对国家经济起着举足轻重的作用[1]。在煤矿开采过程中，如何快速安全实现巷道支护显得尤为重要。由于锚杆支护具有经济成本低、支护效果好、施工速度快等诸多优点，因此被广泛应用，目前已经成为矿井巷道工程最主要的支护形式，而锚杆托板则是锚杆支护系统中的关键构件之一[2-6]。其在锚杆支护系统中起到扩散预应力、增大锚杆的工作阻力、改变围岩状态等重要作用。在受到冲击作用时，围岩与托板间作用力瞬间增加，导致托板出现过载弯折、变形、撕裂等问题，严重影响了巷道锚杆支护效果[7-9]。目前专家学者对锚杆托板的研究主要包括以下3 个方面。一是在托板结构研究方面，郑仰发等[10]采用实验室加载试验研究了不同板厚、不同拱高的方形托板承载力与变形特征，认为托板承载力与钢板厚度、拱高与拱底圆直径之比呈正相关关系；刘双跃等[11]采用理论计算的方法对蝶形托盘的拱形结构进行了力学分析，研究了各参数对托板强度的影响；马永忠等[12]研究了纤维增强复合材质托板的力学特性，获取了非金属托板合理的结构形式和参数。二是在托盘力学性能方面，康红普等[13]测试了煤矿常用托板的力学性能，提出了托盘拱高是影响其承载力的关键因素；贾西阁等[14]、刘少伟等[15]研究了不同材质托板的破坏形式，并分析了影响托板变形破坏的因素。三是在托盘支护作用方面，林健等[16]利用锚杆支护应力场试验台，与金属托板进行比对分析，揭示了木垫板对锚杆预应力的影响规律；陆士良等[17]分析了锚杆预应力在围岩中的分布规律及托板对预应力分布的影响；张剑等[18]针对沿空留巷中托板强度低、锚杆（索）预应力低等问题，通过调整托板尺寸、结构和锚杆预应力，有效控制了沿空留巷围岩变形破坏。以上研究促进了锚杆托板的发展，但也存在少许不足，即荷载作用下不同结构托板的吸能特性尚不明确。为此，研发了1 种新型高延性的微晶格穹顶结构锚杆托板，该托板能够满足理想支护材料的要求，从本质上实现超强吸能特性。研究首先对晶格结构的研究现状进行分析，提出微晶格穹顶结构托板的设计基础及方法；通过 python 编程构建三维微晶格穹顶结构托板模型，采用 Abaqus 平台对静载条件下新型托板的力学特性进行数值模拟，探究材料属性及外形尺寸对新型托板的影响，并分析其吸能特性，选取最优结果。

1 微晶格穹顶结构设计基础

基于以下方程描述的三维麦克斯韦稳定性准则[19]，基于三维支撑拓扑结构的力学响应通常被描述为柔性弯曲主导或刚性拉伸主导：

式中：M为麦克斯韦数；b为杆数；j为节点数。

理想单元形状的示例如图1，其中满足麦克斯韦条件且刚性的孤立细胞被标记为“yes”，而“no”表示麦克斯韦条件不满足。

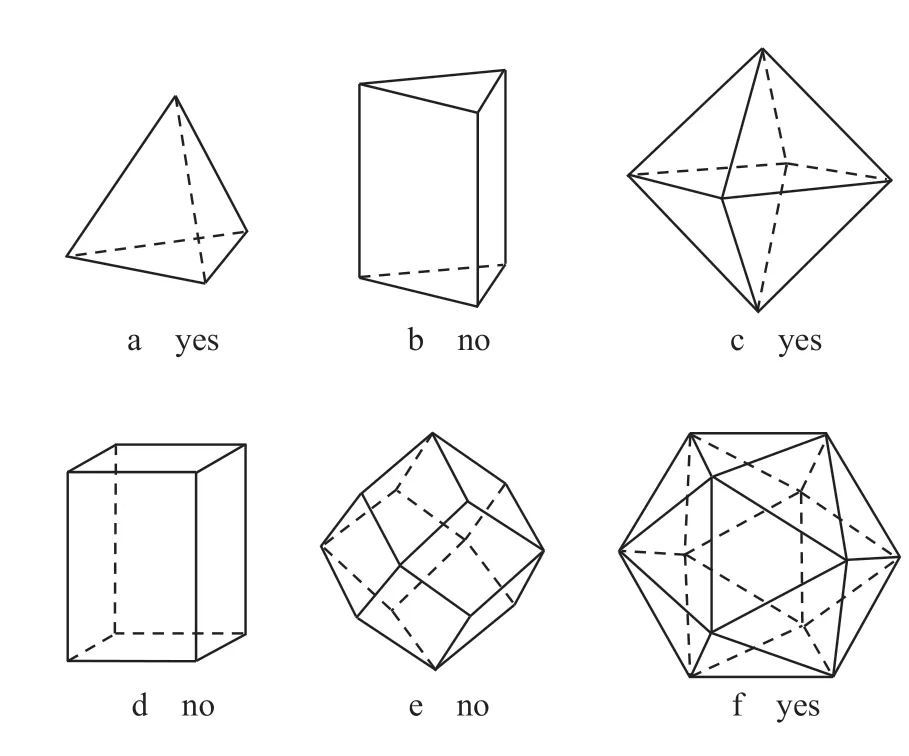
图1 理想单元形状Fig.1 Ideal unit shapes

可以看出，任何具有三角形面的凸简多面体都满足麦克斯韦准则并且是刚性的，四面体和八面体组合在一起填充空间，形成1 个刚性的框架。因此，以拉伸为主的晶格来取代穹顶结构的固体部分比以弯曲为主的晶格更有助于其结构刚度，选择最简单的四面体晶格作为基本的单元拓扑，以取代穹顶结构的实体部分。

2 微晶格穹顶结构设计方法及流程

2.1 晶格结构研究现状

晶格结构是1 种高效的几何构型，由在连接处连接的各个元素组成的网状结构，能够承载一定的受力并实现某种特定的功能。金属三维晶格结构具有比强度高、机械效率高、能量吸收能力强等优良的力学性能，在轻型航空航天、交通运输结构、冲击防护装置等多种工程领域具有广阔的应用前景[20]。为此，大量学者对晶格结构也进行了大量研究。张志等[21]系统地综述了晶格结构的吸能力学特性及其增材制造工艺的研究现状，并展望了晶格结构的设计与增材制造的发展趋势；ZHANG 等[22]提出了具有可控变形特征和可调力学性能的几何梯度晶格结构，发现梯度晶格的变形机理有利于提高能量吸收效率；ZHANG 等[23]建立了自支撑晶格结构对能量吸收的理论力学模型，首次提出1 种能量吸收三维晶格结构的设计方法；WANG 等[24]提出了具有内层层叠单元的新型构型设计，新型晶格构型表现出增强能量吸收能力。结合相关文献，可以充分认识到晶格结构具有强度高、能量吸收能力强等优点。

2.2 设计方法

双向穹顶的基本单元拓扑如图2，其中双层组件相对于中心xz平面对称。此外，每一层都是关于xy和yz平面对称的。

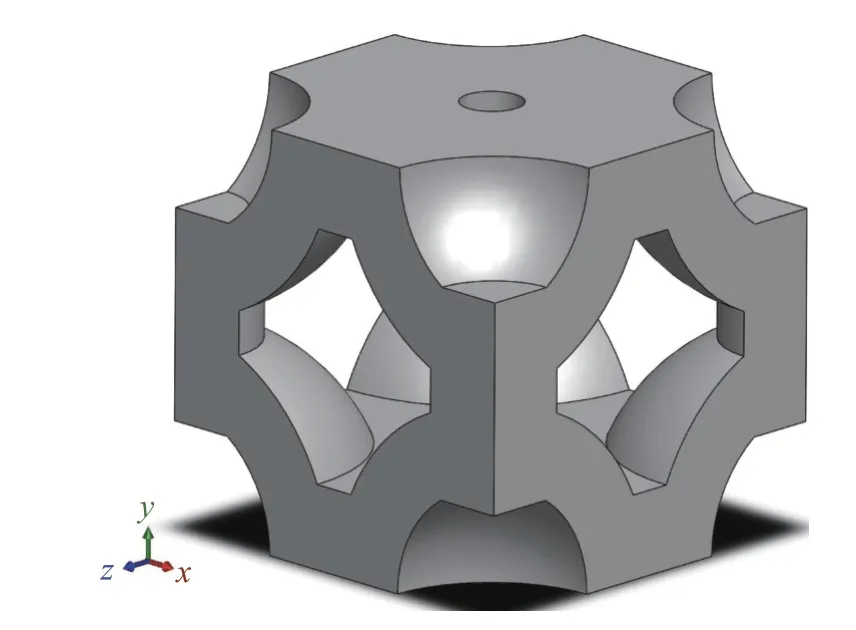
图2 双向穹顶的基本拓扑Fig.2 Basic topology of a two-way dome

与蜂窝、泡沫和晶格的细胞拓扑结构不同，1/4 半球壳的交叉重复排列构成了穹顶结构的基本拓扑如。对于穹顶结构，虽然相对于蜂窝、泡沫和晶格有更高的相对密度，但其独特的半球形截面形状产生了稳定的剪切响应，有助于抑制核心剪切破坏[25-26]，而与钢板的环形接触区域有效地降低了钢板屈曲的风险[27-28]，这是蜂窝和晶格的主要失效模式之一。然而，穹顶结构的刚度及能量吸收比其他蜂窝结构（格子、泡沫和蜂窝）要低得多。为了提高刚度及能量吸收的力学性能，提出将晶格结构和穹顶结构相结合，组成1 种新的结构，称为微晶格穹顶结构，由于其相对于固体材料的优势，微晶格取代了穹顶结构的固体部分；由于是网状框架，其密度较低，比固体材料支持更多的空气以及更少的脆性，因为支柱或支柱对可以单独压缩，而固体材料不能。因此，可以合理地期望微晶格穹顶结构比传统的固体穹顶结构具有更高的强度以及能量吸收能力。

双向穹顶的前视图和结构参数如图3，图中：t为产生单层穹顶的初始厚度；R1、R2为内部和外部穹顶半径；R3为中心孔的半径；h为高度；w为宽度。h和w满足以下约束条件：h=w=2R2。

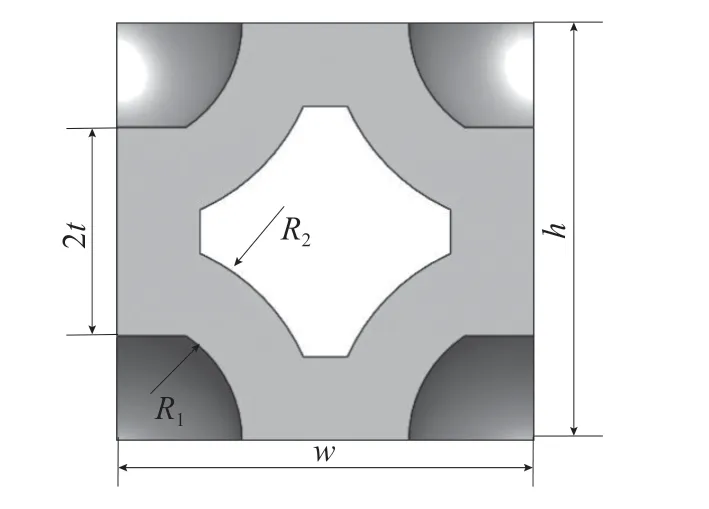
图3 双向穹顶的结构参数Fig.3 Structural parameters of a two-way dome

基于所提出的拉伸主导的四面体晶格可以取代双向穹顶的实体部分，以提高其强度和能量吸收的力学性能的设计理念，将四面体晶格与双向穹顶的组合，微晶格穹顶结构托板如图4，其中四面体微晶格填充双向穹顶的实体部分。

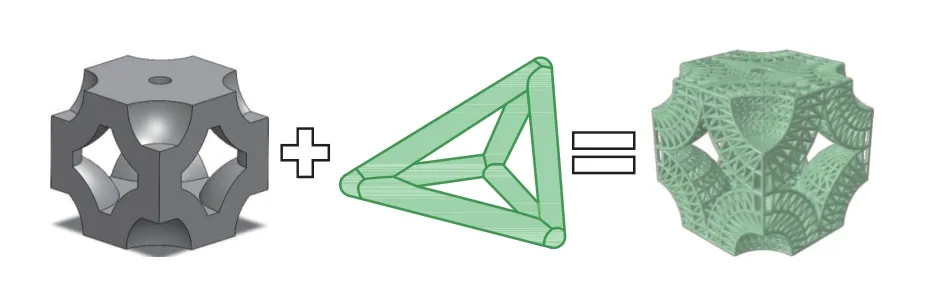
图4 微晶格穹顶结构托板Fig.4 Micro lattice dome structural pallet

可以看出，固体穹顶变成了多孔的微晶格穹顶，减轻了质量，通过这样的组合，更轻的微晶格穹顶比传统的固体穹顶具有更好的吸能力。

2.3 设计流程

在本研究中，设计了1 种具有高强、高吸能特性的微晶格穹顶结构托板，设计步骤如下：

1）预处理。建立三维宏观穹顶结构，并存储各单元及其节点的位置信息，用于拓扑优化。由于四面体单元可划分任意复杂形状的宏观几何网格，因此四面体晶格可以与拓扑优化集成来设计任意几何形状的结构。

2）拓扑优化。在给定的边界条件和体积分数的约束下，通过拓扑优化得到微晶格的均匀密度分布。

3）构建微晶格穹顶结构托板。在获得晶格结构的密度分布后，采用函数关系方法将晶格结构的结构参数与其相对密度联系起来，构建微晶格穹顶结构托板模型。

4）有限元分析。将构建的微晶格穹顶结构托板模型进行有限元分析，通过改变其材料属性及外形尺寸，得到压缩作用下不同模型的模拟结果，对结果进行力学性能分析并选取最优结果。

3 微晶格穹顶结构托板拓扑优化

拓扑优化方法是1 种在设计域内寻求材料最优分布的方法，以设计域中的每一点材料特征为设计变量，采用优化算法，寻求材料在设计域中的有或无来确定最优的拓扑形式，得到结构形状和尺寸特征[29]。

3.1 拓扑优化与晶格结构结合

优化问题一般由目标函数、设计变量和约束条件3 部分组成。基于密度的拓扑优化是在给定的约束条件下，如边界条件和体积分数约束，更新设计变量，如单元的相对密度，直到找到目标函数的最优解，如符合度的最小值。由于研究的目标是使刚度及能量吸收最大化，以微晶格穹顶结构为例，即柔度最小化，选取优化问题中的柔度作为目标函数。拓扑优化用以下方程描述：

式中：c为柔度，目标函数；ρe为单元相对密度设计变量；ke、ue分别为单元刚度矩阵和单元位移矩阵；U为整体节点位移矩阵；K为整体刚度矩阵；N为元素个数；V、V0分别为固体物质体积和所有元素的体积；F为整体节点外载荷矩阵；f为规定的体积分数；ρmax、ρmin分别为相对密度的上界和下界。

用有限元法计算符合度的程序如下：如2.3 节步骤1 可以推导出单元的应变-位移矩阵B，然后用以下公式计算单元应变ε和应力σ，其中D为各向同性元的本构矩阵：

在此基础上，根据虚功原理求出单元刚度矩阵ke：

最后由平衡方程得到整体节点位移矩阵U，再由式（2）计算目标函数柔度。

3.2 拓扑优化模型

提出拓扑优化方法用于寻找均匀的密度分布，以最大限度地提高微晶格穹顶的压缩刚度和能量吸收能力，压缩模型的结构参数见表1。

表1 模型尺寸表Table 1 Model size table

在顶面施加垂直位移，其底面固定。在Abaqus优化模块中设置元素密度最大为0.75，最小为0.25，整体体积分数约束被设置为50%，并采用四面体单元对宏观穹顶结构进行网格划分，网格尺寸选择为10 mm。

3.3 微晶格穹顶结构托板构造

通过拓扑优化得到均匀密度后，下一步是构建三维模型进行有限元分析。在构建过程中，根据单元的密度生成相应的四面体晶格结构，这就需要建立四面体晶格的结构参数与其密度之间的关系。每个四面体晶格的基本结构如图5。

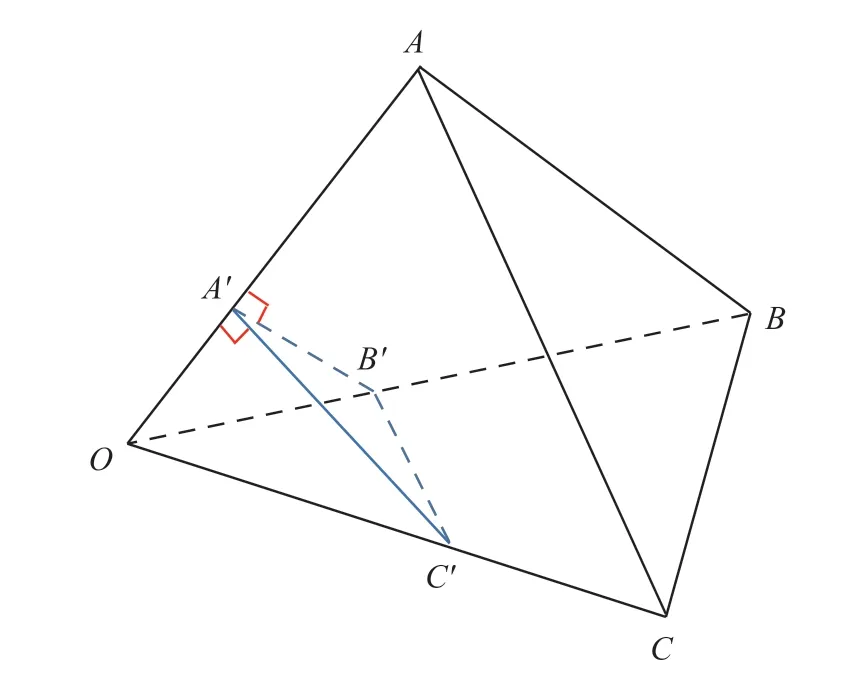
图5 四面体晶格基本结构Fig.5 Basic structure of tetrahedral lattice

每个四面体晶格由6 个半径相同的圆柱体和分布在4 个节点上的球体组成。即，四面体晶格结构的构造可以转化为生成每个节点对应半径的球面和相邻2 个节点之间对应半径的圆柱体操作。因此，只要已知单元密度对应的圆柱体半径，就可以通过 python 脚本在Abaqus 软件中自动生成四面体晶格结构。单元密度与圆柱体半径的关系如下：

四面体晶格的密度 ρe为：

式中：Ve为元素体积；Vs为固体部分的体积。

Ve可以计算为：

式中：xh、yh、zh（h=1,2,3,4）为4 个节点的坐标。

固体部分的体积由完全属于元素的6 个圆柱体组成，四面体晶格实体部分的体积可以通过计算每个圆柱体中属于该固体部分的体积并相加得到。由于每个圆柱体都由相邻的单元共用，所以该单元的体积由柱轴作为公共边的2 个面之间的夹角决定。

以OA边为轴的圆柱体的体积计算为例，说明四面体晶格实体部分的体积计算。设∠BOC=α，∠AOC=β，∠AOB=γ，∠C'A'B'=φ，其中φ为以OA为公边的两面夹角。通过几何计算，可以计算出圆角φ：

式中：φ为表面OAB与表面OAC的夹角。

由于以边OA为轴的圆柱体的体积是由几个相邻单元共用的，所以以OA为轴的圆柱体的体积与整个圆柱体的体积之比为φ/2π，由式（12）计算。

因此，完全属于以边OA为轴的圆柱体的体积VL1为：

式中：L1为节点O到节点A的距离；r为圆柱体的半径。

最后，四面体晶格结构的密度与半径之间的关系可由式（14）得到：

基于均匀化的拓扑优化和晶格结构的构造可用于生成超轻和超细结构。

4 微晶格穹顶结构托板有限元分析

由于试验的局限性，且对比和分析不同材料和尺寸的微晶格穹顶结构托板力学特性时难以快速进行参数调节，材料成本提升的同时也浪费了人力资源。而有限元分析其便捷的模型设计和参数调节能力不仅可以为试验研究和改进提供宏观指导，并且可以较大程度地减小实验量、降低研究成本。本节将利用数值模拟软件 Abaqus 详细介绍了静力压缩全过程，并对模拟结果进行力学性能分析，选取最优结果，为后期3D 打印及应用于现场支护奠定坚实基础。

4.1 模型力学参数及边界条件

根据四面体单元密度与半径的关系，构建三维微晶格穹顶结构托板模型，模型结构参数已在第3.2 节详细描述。在 Abaqus 中将托板模型设置为梁截面，同时赋予梁截面直径为1、2、3 mm 的圆形剖面，3 种不同剖面直径托板模型如图6。不同直径的剖面尺寸则对应以下3 种材料：Q235 钢、ABS 塑料、铝合金，3 种材料的力学参数见表2。

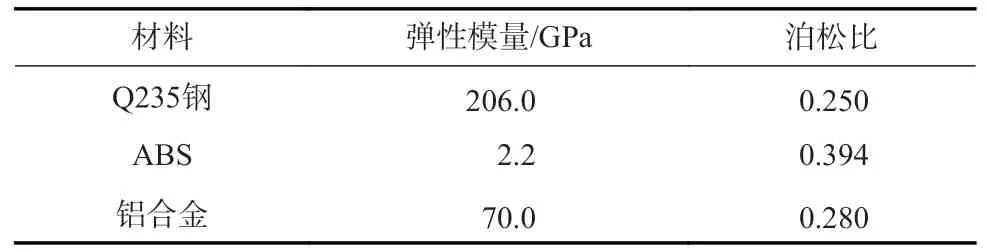
表2 压缩试验的模型力学参数Table 2 Model mechanical parameters of compression tests

图6 不同剖面直径下微晶格穹顶结构锚杆托板Fig.6 Micro lattice dome structure anchor support plate with different profile diameters

根据锚杆托板在实际应用中受压过程，为模型设置上下参考点，将顶面和底面分别与参考点进行耦合，在底面固定的情况下，对顶面施加60 mm 的垂直向下的位移。

4.2 模拟方案

设置托板材料参数及模型尺寸后，为部件进行网格划分，在压缩位移确定的前提下，分别模拟圆形剖面直径在1、2、3 mm 时的压缩试验。

1）截面梁圆形剖面直径为1 mm 时，其他条件不变，分别模拟材料为Q235 钢、ABS 塑料、铝合金的静力压缩试验。

2）截面梁圆形剖面直径为2 mm 时，其他条件不变，分别模拟材料为Q235 钢、ABS 塑料、铝合金的静力压缩试验。

3）截面梁圆形剖面直径为3 mm 时，其他条件不变，分别模拟材料为Q235 钢、ABS 塑料、铝合金的静力压缩试验。

4.3 压缩模拟结果

3 种材料压缩时的应力云图如图7。根据有限元分析结果导出数据绘制载荷-位移曲线，不同直径下3 种材料的载荷-位移曲线如图8。

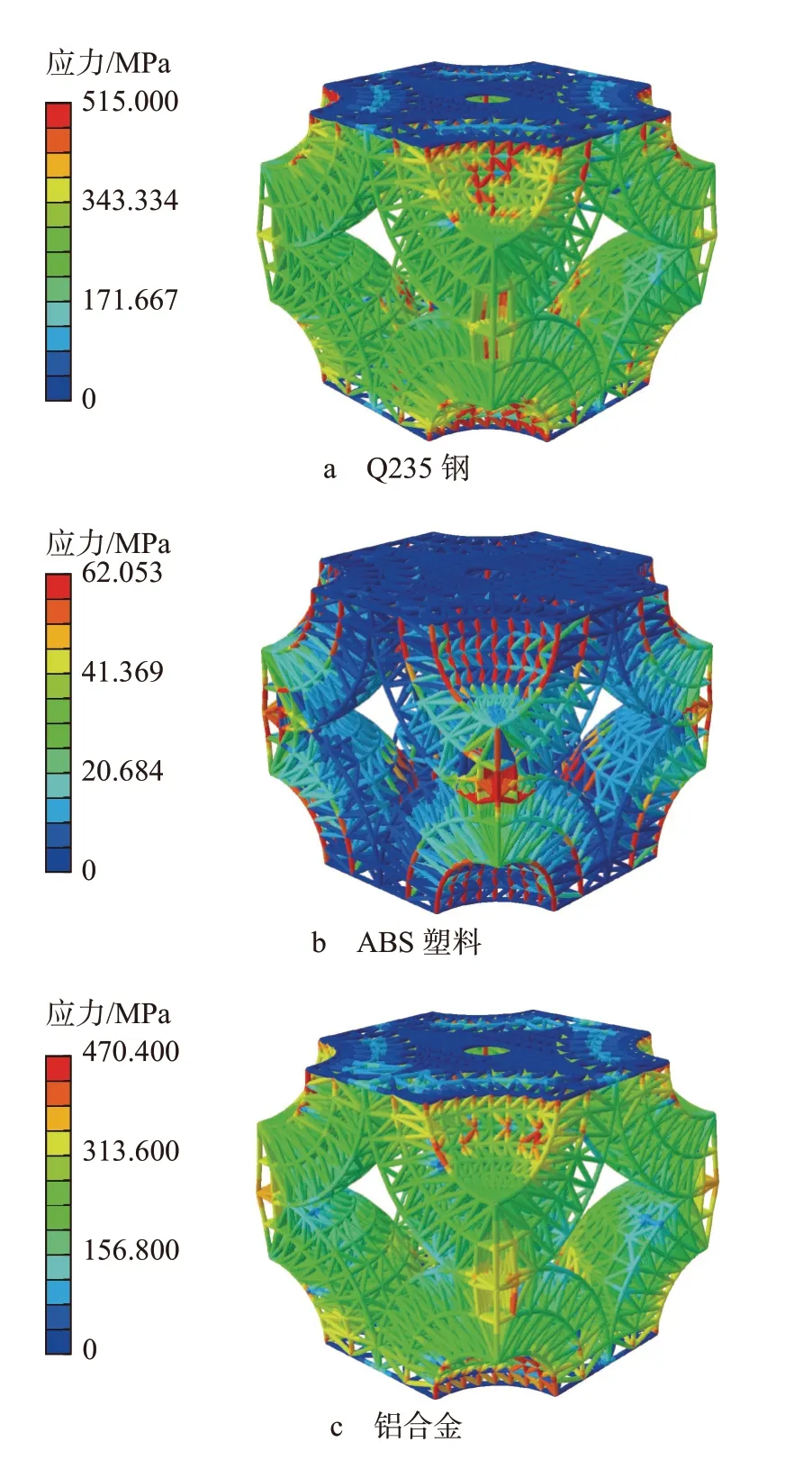
图7 3 种材料压缩云图Fig.7 Compression cloud diagrams of three materials

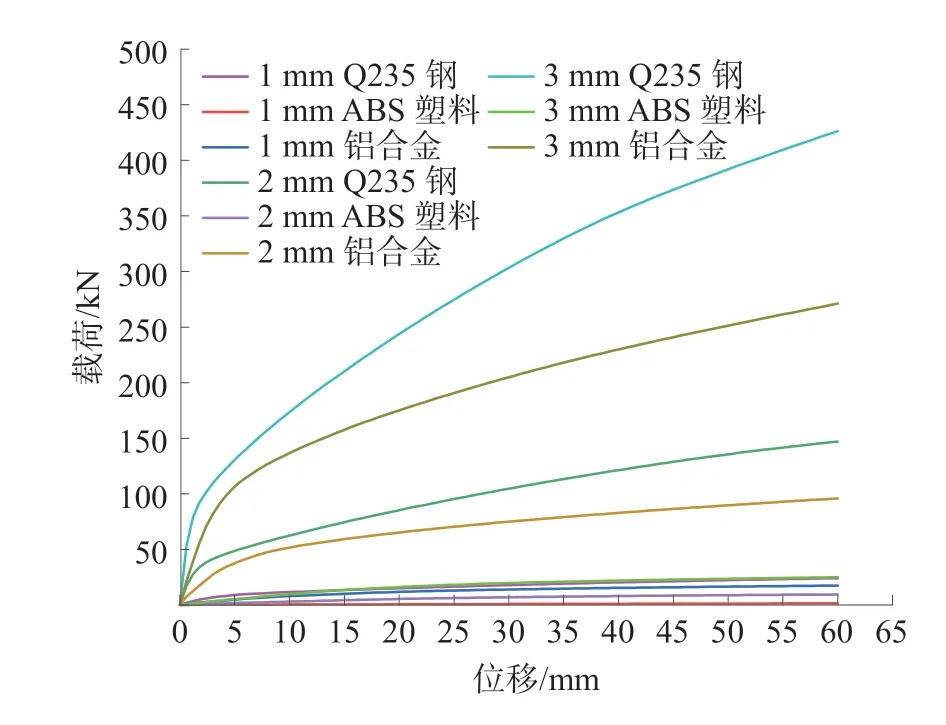
图8 不同直径下3 种材料的载荷-位移曲线Fig.8 Load-displacement curves of three materials at different diameters

由图7，通过对比不同材料的有限元模型的应力分布轮廓，发现刚度大的其应力大，并且不同材料密度高的区域应力较大，而密度低的区域应力较小，通过增加高应力区域的材料用量和减少低应力区域的材料用量是减少材料用量的有效策略。

由图8 可以看出：在相同的剖面直径下，Q235 钢比ABS 塑料和铝合金材料提高微晶格穹顶结构托板的承载力效果更为显著，并且Q235 钢和铝合金材料载荷增加具有明显相同的趋势，都将随着压缩位移的增加，在一定范围内载荷迅速增加，而后缓慢增加；而ABS 塑料一直是缓慢增加，增加速度低于另外2 种材料，载荷最大值远小于另外2 种材料；在不同的剖面直径下，3 种材料的载荷都将随着剖面直径的增加而提高。

为了更好地比较不同材料以及不同剖面直径对微晶格穹顶结构托板载荷的影响，汇总了3 种材料在压缩位移相同时不同剖面直径下的载荷，载荷汇总表见表3，不同直径下不同材料的微晶格穹顶结构托板的载荷增长曲线如图9。

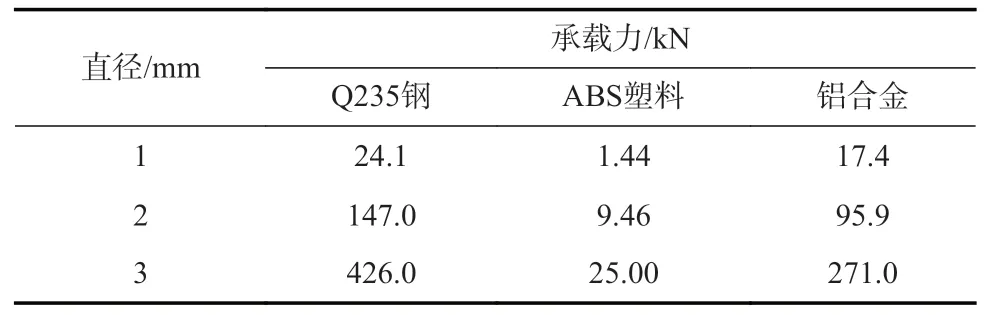
表3 载荷汇总表Table 3 Load summary table

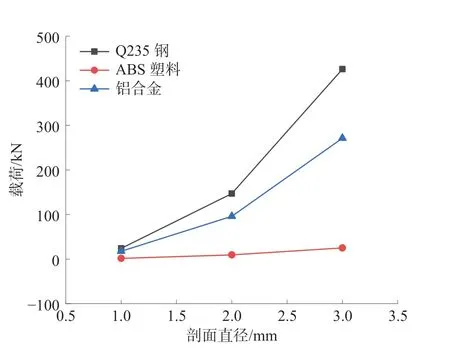
图9 不同剖面直径下3 种材料的载荷曲线Fig.9 Load curves of three materials with different profile diameters

由表3 可以看出：3 种材料在相同剖面直径下承载力大小顺序为：Q235 钢＞铝合金＞ABS 塑料，当剖面直径为3 mm 时，Q235 钢承载力最高，约为4.26×105N，具有高强度。

由图9 可知：Q235 钢、ABS 塑料、铝合金3种材料在剖面直径2 mm 时，载荷的提升幅度分别为510%、556.94%和451.15%，而在剖面直径3 mm 时，载荷提升幅度分别为189.8%、164.27%和182.59%，随着剖面直径的增加，载荷的提升幅度逐渐减小。

为了探究3 种材料在不同剖面直径下能量吸收的大小，计算了载荷-位移曲线与水平轴围成区域的面积，能量吸收的大小汇总表见表4，不同剖面直径下能量吸收的大小如图10。

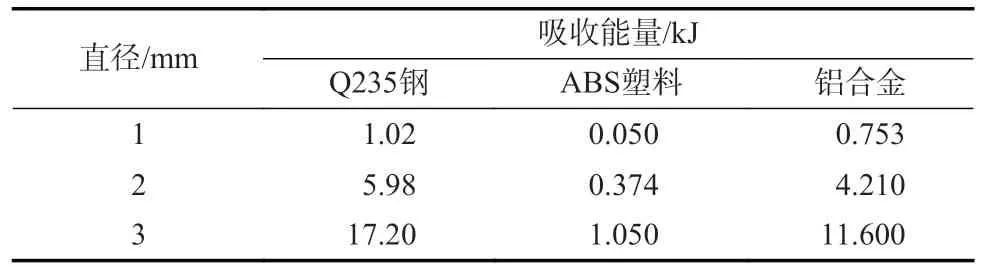
表4 能量吸收大小汇总表Table 4 Summary table of energy absorption size

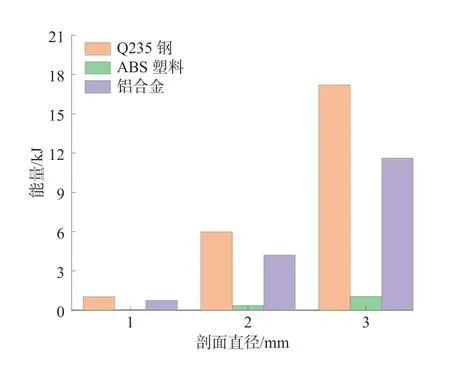
图10 不同剖面直径下能量吸收的大小Fig.10 Energy absorption per unit length under different section diameters

由表4 及图10 可以看出：随着剖面直径的增加，3 种材料的能量吸收都有所提高，Q235 钢能量吸收增加尤为明显，而ABS 塑料能量吸收增加最慢；3 种材料的能量吸收大小顺序都为：Q235钢＞铝合金＞ABS 塑料，当剖面直径为3 mm时，Q235 钢能量吸收最大，约为1.72×104J，具有高吸能特性。

综上所述，当微晶格穹顶结构托板的剖面直径为3 mm，材料为Q235 钢时，为数值模拟的最优结果，此时，微晶格穹顶结构托板具有高强、高吸能特性。此结果将为后期3D 打印，应用于现场支护奠定基础。