基于CEEMDAN-MFDE-HHO-SVM的机载燃油泵故障辨识*
2023-10-26刘军龙俞凯耀张相春
刘军龙,俞凯耀,张相春
(1.遵义师范学院 资源与环境学院,贵州 遵义 563006;2.浙江国际海运职业技术学院 海洋装备工程学院,浙江 舟山 316012;3.遵义师范学院 生物与农业科技学院(食品科技学院),贵州 遵义 563006)
0 引 言
机载燃油泵为航空发动机输送标准压力和流量的燃油。机载燃油泵的工作环境非常复杂,运行中可能出现故障[1],因此,有必要建立智能的故障辨识模型,以准确辨识机载燃油系统的故障。
针对机载燃油泵的故障辨识,李娟等人[2]采用样本分位数提取了故障特征,对故障进行了准确辨识;但该方法需要合理布置传感器。焦晓璇等人[3]采用小波包处理机载燃油泵振动信号,精确地识别了机载燃油泵的故障;但小波包的性能依赖于小波基的合理设置。戴邵武等人[4]5-7提出了模糊信息粒化和模糊熵相结合的故障诊断方法,准确地识别了机载燃油泵故障;但模糊熵只用于进行单一尺度的分析,对特征的提取不够全面。戴邵武等人[5]11-13提出了基于多尺度模糊熵的特征提取方法,提高了特征提取的质量;但振动信号中包含噪声,需要去除其中的噪声。为此,JIAO Xiao-xuan等人[6]将经验模态分解用于机载燃油泵的信号降噪,去除了信号中的噪声;但经验模态分解存在严重的模态混叠和端点效应缺陷。鲍杰等人[7]提出了基于完备集成经验模态分解的故障诊断方法,增强了信号降噪效果;但该方法引入的白噪声会导致其分解的分量中残留噪声。章余等人[8]采用改进的卷积神经网络和支持向量机,对机载燃油泵故障进行了诊断,对故障进行了精确识别;但该方法的性能受参数的影响较大。
机载燃油泵振动表现为非线性,需要采用非线性方法进行处理。
HOU Jing-bao等人[9]采用集成经验模态分解和排列熵,对滚动轴承进行了故障诊断,准确诊断了轴承故障;但该方法的效率非常低下,不适宜处理大批量数据。CHEN Jia-yu等人[10]采用完备集成经验模态分解方法,对齿轮箱进行了故障诊断,证明了完备集成经验模态分解方法可以提高诊断效率,并减小诊断误差;然而,该方法的分解精度有待提高。
在对振动信号进行降噪后,需要采用特征提取方法以构建故障特征。目前,特征提取方法以样本熵、模糊熵、排列熵和散布熵为代表。
戴邵武等人[4]2-4提出了基于模糊信息粒化和模糊熵的故障诊断方法,准确诊断了机载燃油泵故障;但该方法仅提取每个信息粒的模糊熵,忽视了每个粒子的多尺度特征,特征表达得不够全面。为实现信号的多尺度分析,DAI Hong-de等人[5]5-7采用一种基于多尺度模糊熵的方法,有效提取了机载燃油泵的故障特征;但该方法忽视了信号中的噪声。
在提取了故障特征后,需要选择合适的分类器进行故障识别。陈俊柏等人[11]采用遗传算法对支持向量机的参数进行了优化,对机载燃油泵故障进行了有效识别;但遗传算法的全局寻优能力较差,易陷入局部最优。焦晓璇等人[12]采用粒子群算法,对支持向量机进行了参数优化,取得了优于遗传算法的优化结果;但粒子群算法的迭代速度较慢,且全局优化性能不佳。
针对上述问题,笔者提出一种基于自适应噪声完备经验模态分解(CEEMDAN)、多尺度波动散布熵(MFDE)和哈里斯鹰(HHO)算法优化支持向量机(SVM)的损伤识别模型。
首先,笔者利用CEEMDAN方法对振动信号进行分解,并进行信号重构;随后,利用MFDE方法提取重构信号的故障特征;最后,利用哈里斯鹰算法,对支持向量机的参数进行优化,构建HHO-SVM故障分类模型,进行机载燃油泵的故障辨识。
1 算法原理
1.1 自适应噪声完备经验模态分解信号重构
为分析机载燃油泵振动信号,使振动信号中不同的模态分量解耦,笔者采用自适应噪声完备经验模态分解(CEEMDAN)方法,对振动信号进行分解,生成1组本征模态分量(IMF),突出振动信号的故障特征。但该方法分解得到的IMF分量依然不可避免地存在伪分量和残余噪声。
为确定有用分量,避免相关系数指标错误地应用于评估分量的重要性[13],笔者利用能量占比对分量执行进一步的选择。对于信号的能量来说,占比越大,则包含的故障信息也越多[14]。因此,可以通过相关系数—能量对IMF分量进行筛选和重构。
具体步骤如下:
1)对于振动信号x(t),利用CEEMDAN方法进行分解,得到IMF分量;
2)计算各IMF与原信号的相关系数以及能量占比;
3)选择相关系数大于0.1,且能量比大于5%的IMF分量进行重构。
1.2 多尺度波动散布熵方法原理
波动散布熵无法对信号进行多尺度分析。为此,AZAMI H等人[15]将其与粗粒化处理相结合,提出了MFDE方法。
首先,原始信号为{u1,u2,…ub,…,uN},利用向下取整,将其分割为互不重叠的子序列;接着求出每个子序列的均值,生成序列,即:
(1)
式中:τ为尺度因子;[]为向下取整函数;N为信号长度。
然后,在各尺度因子τ下,计算各子序列的波动散布熵,从而得到了MFDE方法。
1.3 哈里斯鹰算法优化支持向量机方法
支持向量机(SVM)目前已被广泛应用于识别领域[16],但应用SVM方法时必须选择合理的参数。为此,笔者利用哈里斯鹰优化算法,对SVM方法的惩罚系数C和核函数g进行寻优,以增强分类器的性能[17]。
1.3.1 哈里斯鹰算法
哈里斯鹰优化(HHO)算法是一种受到哈里斯鹰捕猎行为启发的优化算法。HHO算法包括全局搜索、转换和局部开发3个阶段[18-19]。
在全局搜索阶段,哈里斯鹰在搜索空间中随机分布,基于2种不同的方案来寻找空间中的猎物,并进行方位更新。其模型如下:
(2)
(3)
式中:Xt+1为鹰在第t+1次迭代时的坐标;Xt为鹰在第t次迭代时的坐标;Xrand为第t次迭代时鹰的随机坐标;Xr为第t次迭代时鹰的猎物坐标;Xm,t为第t次迭代时鹰的平均坐标;r0,r1,r2,r3,r4,q为[0,1]范围内的随机值;ub为搜索空间的上界;lb为搜索空间的下界。
在转换阶段,HHO算法利用猎物能量E来转换搜索和开发,模型如下:

(4)
式中:T为迭代最大次数;E0为[-1,1]的随机值。
在局部开发阶段,为准确模仿哈里斯鹰的真实捕猎动作,笔者依据哈里斯鹰的不同捕猎策略开发了4种方法,对开发环节进行更新,并根据猎物能量E和逃逸因子η来选择不同方法。
1)软围猎
当|E|≥0.5且η≥0.5时,猎物能量E丰富,可以利用跳跃策略来逃脱围猎,鹰通过消耗E,最后成功抓获猎物。其坐标更新如下:
Xt+1=ΔXt-E|JXr,t-Xt|
(5)
ΔXt=Xr,t-Xt
(6)
J=2(1-r5)
(7)
式中:J为猎物跳跃强度;r5为[0,1]的随机值。
2)硬围猎
当|E|<0.5且η≥0.5时,猎物由于能量E的缺乏而被鹰抓获。其坐标更新如下:
Xt+1=Xr,t-E|ΔXt|
(8)
3)渐进式快速俯冲软围猎
当|E|≥0.5且η<0.5时,猎物能量E丰富,具备躲避围猎的能力。首先,鹰对猎物执行俯冲式的袭击,若袭击不成功,则贯彻随机游走方法。
其模型定义如下:
(9)
式中:D为项目维数;S为1×D维随机向量。
LF定义如下:
(10)
式中:LF(x)为Levy飞行函数。
4)渐进式快速俯冲硬围猎
当|E|<0.5且η<0.5时,猎物能量E缺乏,鹰在袭击猎物之前会开展硬围猎进行捕猎,若袭击不成功,则进行随机游走行动。
其模型定义如下:
(11)
1.3.2 哈里斯鹰算法优化支持向量机流程
HHO方法优化支持向量机的步骤如下:
1)将哈里斯鹰种群数量(N)、迭代总数(T)、搜索范围的上界与下界都进行初始化;
2)采用测试样本的分类准确率作为适应度函数,以具有最佳适应度值的哈里斯鹰作为全局最佳解;
3)更新猎物逃逸能量、依据能量E,更新哈里斯鹰在搜索或开发阶段中的策略;
4)求出哈里斯鹰更新坐标后的个体适应度,若更新后的适应度优于猎物的适应度,则将该适应度对应的坐标作为猎物的新坐标;
5)重复步骤3)和4),直至完成全部的迭代过程,最后猎物的最佳坐标信息为SVM方法的最佳参数组合。
2 基于CEEMDAN-MFDE和HHO-SVM的辨识方法
在算法原理的基础上,笔者建立基于CEEMDAN-MFDE联合HHO-SVM的机载燃油泵故障辨识模型。其具体步骤如下:
1)信号获取。利用加速度计采集机载燃油泵的振动信号;
2)信号分解。利用CEEMDAN方法对机载燃油泵振动信号进行分解,获得IMF分量;
3)信号重构。分别求解各IMF分量的相关系数和能量比,筛选获得包含丰富信息的IMF分量,进行信号重构;
4)特征提取。对重构信号进行MFDE分析,得到维度为τ的波动散布熵值,将其作为特征向量;
5)故障辨识。将特征向量输入至HHO-SVM分类器,进行分类,完成机载燃油泵的故障辨识。
机载燃油泵故障诊断方法的流程图,如图1所示。
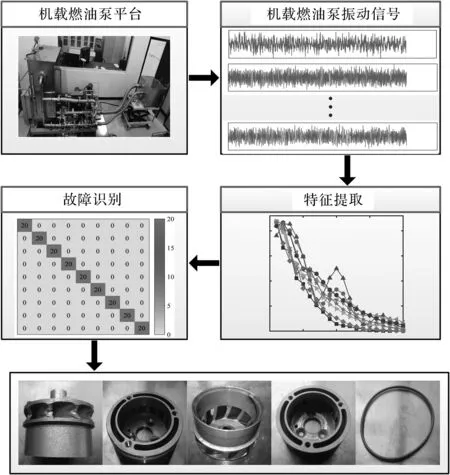
图1 机载燃油泵故障诊断方法的流程图
3 实验数据分析与对比
此处的实验数据来自于PAN Jin-xin等人[20]提供的数据集。
实验选取了某型机载燃油泵(离心泵)为研究目标。工作时,该泵采用电机驱动离心叶轮旋转,对燃油进行增压,将燃油输出至发动机。
机载燃油泵的具体参数如表1所示。

表1 机载燃油泵的参数
笔者对机载燃油泵的不同工况进行了研究,分别是正常(S1)、扩散管损伤(S2)、泄露(S3)、叶轮与泵口刮蹭(S4)、叶轮与扩散管刮蹭(S5)、叶片损伤1片(S6)、叶片损伤2片(S7)、叶片损伤10片+扩散管损伤(S8)、叶片损伤10片(S9),共9种工况。
典型的故障工况如图2所示。

图2 机载燃油泵的典型故障
笔者在机载燃油泵实验平台采集振动信号,加速度计布置于燃油泵电机的壳体上,电机为变频电机,转速为5 600 r/min。
机载燃油泵实验平台如图3所示。

图3 机载燃油泵实验平台
笔者以6 000 Hz的频率采集振动信号,将每种工况的振动数据分为长度1 024的样本各40组(其中,20组作为训练集,剩余20组作为测试样本)。
3.1 故障特征提取
9种工况的振动信号如图4所示。

图4 机载燃油泵9种工况的振动信号
由图4可以发现:振动信号不具备明显的特征,无法根据波形来区分不同工况。
笔者以扩散管损伤样本为例,进行CEEMDAN分解,得到一组IMF分量;随后,分别计算各IMF的相关系数和能量比,将相关系数大于0.1和能量比大于5%的分量进行信号重构。
各IMF分量的相关系数、能量比如表2所示。

表2 各IMF分量相关系数—能量比
从表2可以发现:IMF1、IMF2符合相关系数—能量比的标准,因此,笔者选择这2个分量进行信号重构。
扩散管损伤的重构信号如图5所示。
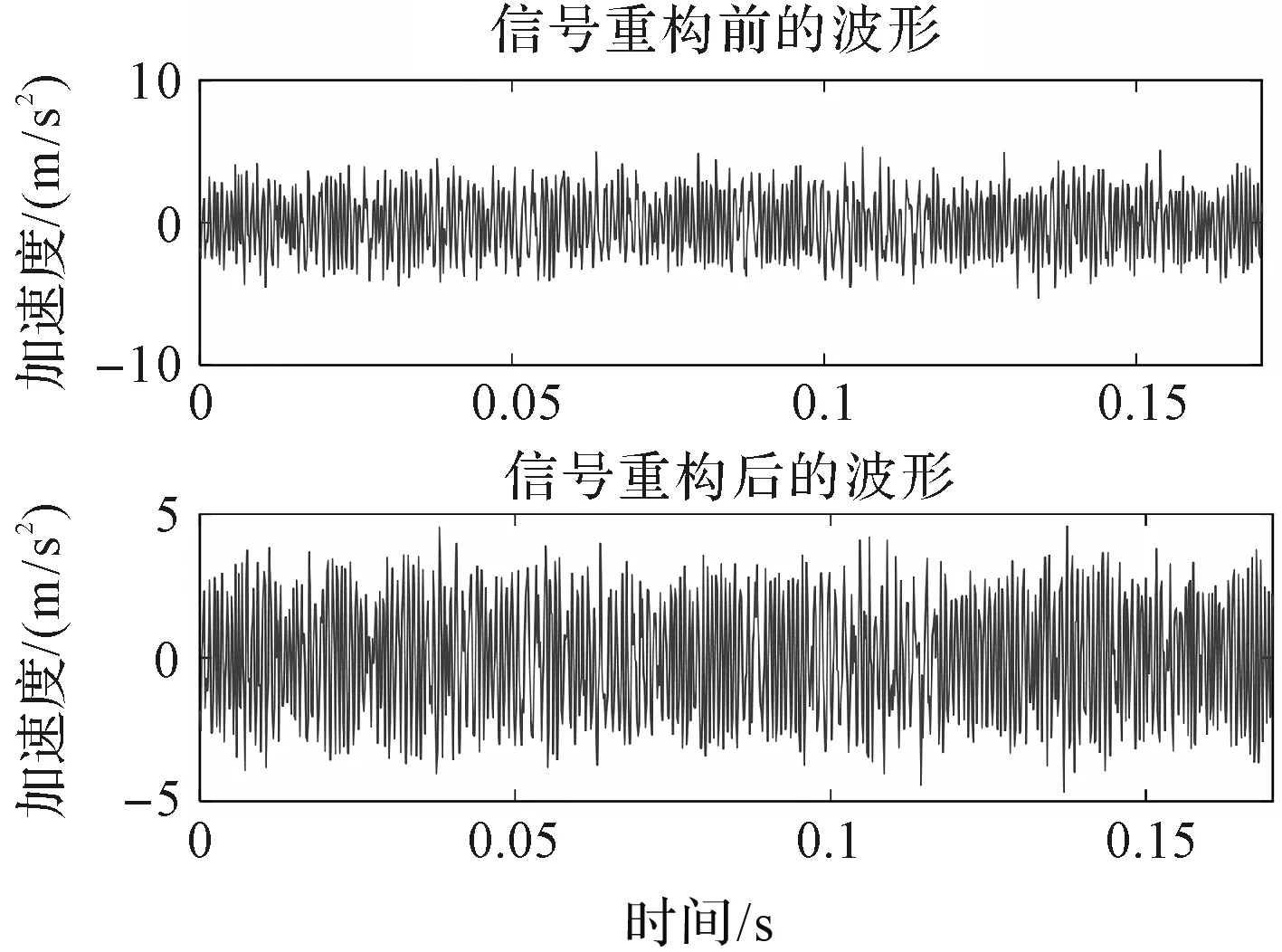
图5 信号重构前后的时域波形图
由图5可以发现:重构信号的振幅出现了损伤,但是振动信号中的冲击分量更加明显,表明对信号进行降噪能够减小干扰,突出信号中的冲击信息。
笔者利用MFDE方法对重构信号进行了特征提取。MFDE方法需要设置3个参数,即嵌入维数m、类别数c和时间延迟d。针对这3个参数已经有较多文献进行了研究,笔者不再赘述。笔者设置m为2,c为5,d为1,尺度因子为20。
9种工况的MFDE值如图6所示。
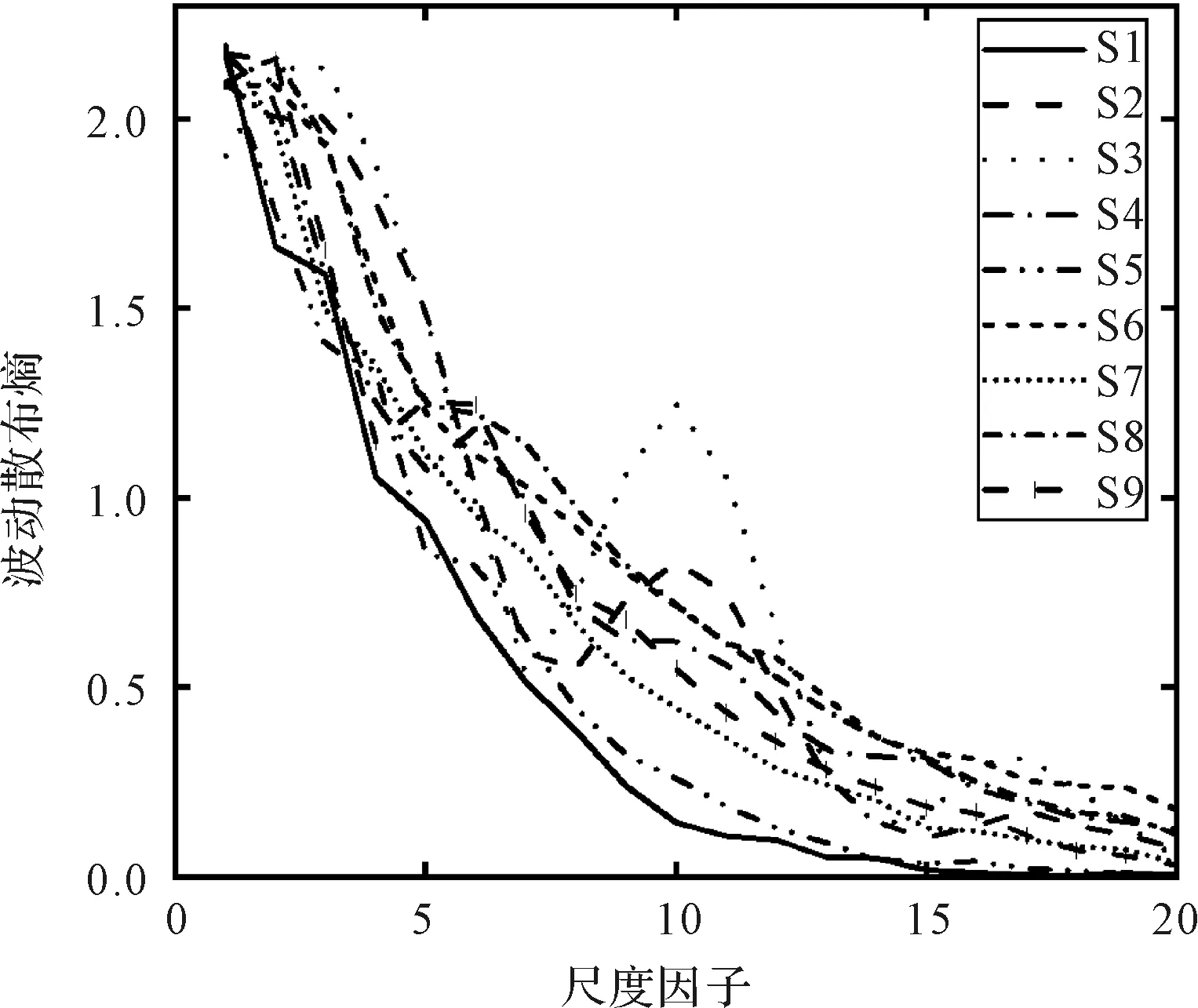
图6 9种工况的MFDE值
由图6可以发现:9种工况的MFDE值具有类似的趋势,即熵值随着尺度因子的增加而减小;同时不同工况的振动信号具有不同的动力学特性,而采用MFDE方法能够将这种差异反映出来。
在大多数尺度下,MFDE值具有比较好的区分度,证明MFDE方法可以用于有效区分不同振动信号的复杂度。
3.2 故障识别
笔者采用HHO方法,对SVM方法的惩罚系数和核函数进行寻优,每组工况有40组样本(其中,20组作为训练样本,另一部分作为测试样本)。
识别结果如图7所示。
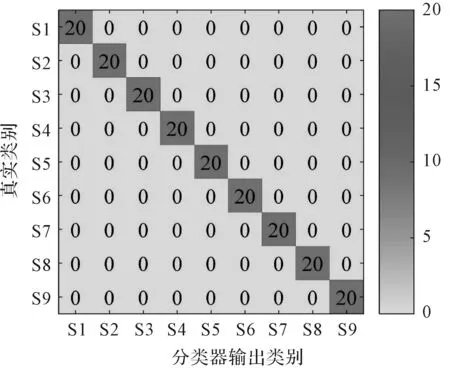
图7 CEEMDAN-MFDE-HHO-SVM识别结果
由图7可以发现:每个类别的样本都未出现错误识别的样本,证明了该方法的有效性。
3.3 方法对比验证
为了验证多种方法的优劣,笔者从3个角度来评估CEEMDAN-MFDE-HHO&SVM的性能,分别是:
1)信号处理方法:集成经验模态分解(ensemble empirical mode decomposition,EEMD)、未采用信号预处理方法);
2)熵值特征提取方法:多尺度散布熵(multiscale dispersion entropy,MDE)、多尺度模糊熵(multiscale fuzzy entropy,MFE)和多尺度样本熵(multiscale sample entropy,MSE);
3)优化算法:遗传算法(genetic algorithm,GA)、粒子群算法(particle swarm optimization,PSO)。
3.3.1 信号处理方法对比
笔者将CEEMDAN-MFDE特征提取方法分别与EEMD-MFDE、MFDE特征提取方法进行对比,将由这3种方法提取的故障特征输入至HHO-SVM分类器,进行故障特征识别(训练样本和测试样本的比例保持一致)。
采用基于EEMD-MFDE以及MFDE方法得到的诊断结果,如表3所示。

表3 3种特征提取方法的诊断结果对比
由表3可知:CEEMDAN-MFDE方法的准确率高于EEMD-MFDE方法,证明CEEMDAN方法在处理机载燃油泵振动信号方面优于EEMD方法,这是因为EEMD方法处理后的信号并未充分消除噪声的影响;
此外,基于CEEMDAN-MFDE方法和EEMD-MFDE方法的准确率均高于MFDE方法,这是因为MFDE方法未对信号进行降噪处理,进而降低了特征的质量(这也直接证明了对信号进行降噪的必要性)。
3.3.2 熵值特征提取方法对比
为了验证MFDE方法在特征提取中的有效性,笔者将其与MDE方法、MFE方法和MSE方法进行对比。其中,MFE方法和MSE方法的参数设置为:嵌入维数为2,相似容限为0.2,模糊参数为2,时间延迟为1,在对比中,仅将MFDE替换为MDE、MFE和MSE,其余操作不变。
诊断结果如表4所示。
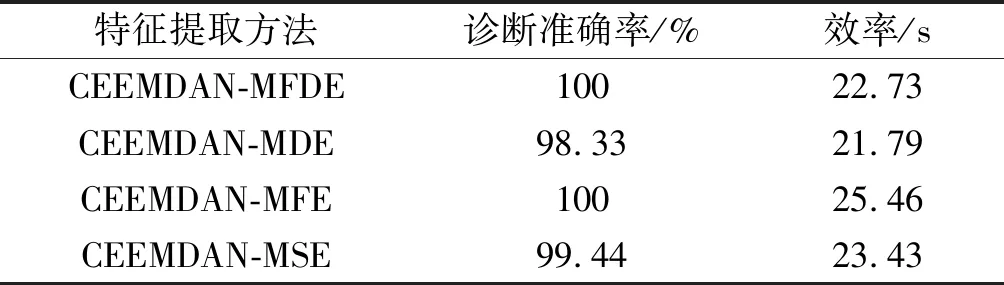
表4 4种特征提取方法的诊断结果对比
从表4可知:CEEMDAN-MFDE和CEEMDAN-MFE方法均获得了100%的准确率,证明这2种方法均可以有效提取机载燃油泵信号的故障特征;CEEMDAN-MDE和CEEMDAN-MSE的准确率均低于CEEMDAN-MFDE,证明CEEMDAN-MFDE的优越性;此外,虽然MFE取得了比较不错的结果,但其特征提取效率偏低,计算花费高于MFDE。
由此可见,CEEMDAN-MFDE方法是其中最优的。
3.3.3 不同分类器对比
为了证明HHO-SVM在故障识别中更有优势,笔者将HHO-SVM分类器与GA-SVM分类器、PSO-SVM分类器进行对比。
笔者将由CEEMDAN-MFDE提取的故障特征输入到GA-SVM和PSO-SVM中,得到了不同分类器的故障诊断对比结果,如表5所示。
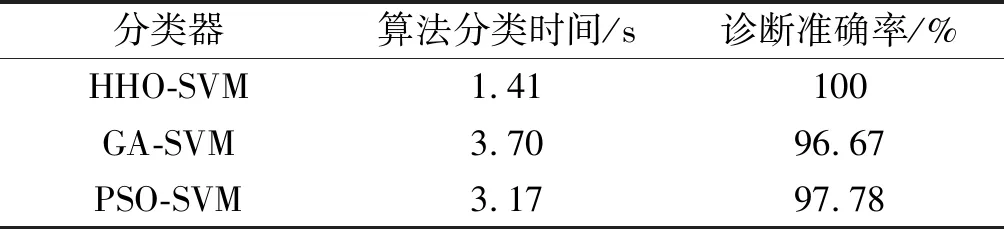
表5 不同分类器诊断结果对比
由表5可知:相比于其他分类器,基于HHO-SVM的分类器不仅具有最高的准确率,而且效率也更高。
这证明HHO算法能够在较短的时间里搜寻到更优的参数组合,在机载燃油泵的故障辨识中具有更好的性能。
从不同角度的对比结果可以发现,笔者建立的损伤识别模型在一定程度上优于其他混合故障识别模型,在机载燃油泵的损伤识别中具有应用潜力。
4 结束语
针对机载燃油泵的故障识别问题,笔者提出了一种将CEEMDAN、MFDE和HHO-SVM相结合的机载燃油泵故障辨识方法,利用实测机载燃油泵振动数据集对该方法进行了实验评估。
研究结论如下:
1)采用CEEMDAN进行信号重构和MFDE特征提取,采用基于CEEMDAN-MFDE的特征提取方法,能够取得100%的故障识别准确率,具备应用于机载燃油泵故障识别的潜力;
2)笔者提出的CEEMDAN-MFDE和HHO-SVM故障诊断策略取得了100%的故障识别准确率。在信号处理方面,CEEMDAN-MFDE优于EEMD-MFDE和MFDE,这2种方法的准确率分别为98.89%和95.56%;而在熵值特征提取方面,MFDE的准确率高达100%,且效率为22.73 s,优于MDE、MFE和MSE,3种方法的准确率分别为98.33%、100%和99.44%,而效率分别为21.79 s、25.46 s和23.43 s;在分类器方面,HHO-SVM的诊断准确率为100%,诊断时间为1.41 s,优于GA-SVM和PSO-SVM。
虽然采用CEEMDAN-MFDE-HHO-SVM方法得到了较高的故障诊断准确率,但其效率还有待于提升。因此,笔者未来将就减小特征数量、增加特征提取效率的可行性进行深入的探讨。
