齿轮传动系统可靠性快速建模的数字化分析方法*
2023-10-26韩莹莹艾红旭李梓源
韩莹莹,艾红旭,申 强,李梓源,李 威*
(1.中国船舶集团有限公司第七〇三研究所,黑龙江 哈尔滨 150078;2.北京科技大学 机械工程学院,北京 100083)
0 引 言
机械系统的可靠性研究主要包括可靠性设计、分配、建模、分析、评价和改进等方面的内容。只有创建正确合理的模型,采用正确的分析方法,才能得到准确的可靠性评价结果,进而找出系统的薄弱环节,为系统可靠性设计提供依据,并制定相应的改进措施。
PFEUFER T[1]利用模型算法,对汽车的执行器进行了可靠性分析,在冗余方案的扩展中,基于模型算法的故障诊断方法有利于早期故障信号的检测;但是,其未对参数化建模进行探究。何晓聪等人[2]研究了威布尔分布在齿轮减速器中应用,应用威布尔分布理论,导出了二级直齿圆柱齿轮减速器的一种寿命可靠性模型;但是,在模型中该研究只考虑了齿轮和轴承的可靠性,没有考虑轴的可靠性。王正等人[3]综合运用应力-强度干涉模型、顺序统计量理论、泊松随机过程以及概率微分方程,建立了零件的动态可靠性模型;但是,其未研究系统的可靠性建模方法。SADOU N等人[4]利用Petri网对动态系统进行了可靠性分析,提出了一种在Petri网中预测可能出现故障情况的方法;但对于复杂的系统,该方法会导致状态空间爆炸。ZHANG G等人[5]建立了kriging可靠性模型,简化了应力强度干涉模型的计算,并对大型球磨机齿轮传动系统进行了可靠性计算;但是,在模型中其只考虑了齿轮的可靠性,没有考虑轴承的可靠性。李春玲等人[6]依据零部件相关寿命,对风电齿轮箱太阳轮进行了可靠性建模;但是,其未对行星轮进行可靠性建模。孙道明等人[7]在考虑了失效模式相关性的条件下,对齿轮进行了可靠性建模,采用Monte Carlo仿真方法,得到了齿轮在两种失效模式下极限状态函数的散点图;但是,其对于齿轮传动系统可靠性的研究多落脚于单一零件故障模式下的可靠性模型,缺乏对考虑各个零件载荷相关性的齿轮传动系统整体进行可靠性建模。
RASHID H S J等人[8]利用影响图,对直升机变速箱进行了可靠性建模,针对主齿轮箱(main gear box,MGB)油系统相关事故,建立了安全风险模型;但是,其仅给出了关系模型,没有给出相应的数学模型。XIE L等人[9]基于时域级数,对齿轮箱进行了可靠性建模,并定义了时域级联系统;但是,其未分析各级之间的相互耦合关系。王春华等人[10]以可靠性等为约束条件,选取体积、重合度和传动效率作为目标函数,利用改进粒子群算法,对行星齿轮传动进行了多目标可靠性优化设计;但是,在优化设计模型中,其只考虑了太阳轮和行星轮,没有考虑齿圈。于格等人[11]基于可信度,建立了齿轮可靠性模型,给出了基于性能裕量确信的可靠度计算流程和算法;但是,其仅对单级齿轮传动系统进行了研究,没有对多级齿轮系统进行探究。李明凯等人[12]研究了基于参数不确定条件下的齿轮弯曲疲劳可靠性计算及灵敏度分析方法;但是,其只开展了高应力区的成组法试验,没有开展低应力区的升降法试验。QIAN H等人[13]基于Kriging模型,在多种故障模式下,对旋转矢量(rotation vector,RV)减速器进行了时变可靠性建模分析;但是,其仅考虑了齿轮接触和弯曲疲劳失效,未考虑齿面胶合失效。王春光等人[14]以系统动力学、可靠性、稳健性和体积作为目标函数,建立了直齿轮箱的可靠性稳健优化设计模型;但其没有对斜齿轮进行探究。裴帮等人[15]以疲劳实验数据为基础,对某地铁齿轮可靠性进行了分析;但是,其未考虑齿轮共因失效的影响。
由于齿轮传动系统在实际工程使用过程中变得越来越复杂,由此带来建模计算量越来越大、效率越来越低,因此,急需开展齿轮传动系统可靠性快速建模数字化研究,以及开展相应软件的开发工作。
针对复杂机械系统可靠性建模计算量大和耗时长等问题,综合应力-强度干涉模型和载荷相关性,笔者建立定轴轮系、行星轮系及混合轮系的可靠性模型,设计开发齿轮传动系统可靠性数字化建模软件,完成参数化建模与自动化分析;最后,以功率分支齿轮传动系统为例,采用解析法和数字化软件,对其进行可靠性建模与分析,对可靠性快速建模数字化分析平台的有效性进行验证。
1 基于载荷相关性的系统可靠性模型
齿轮传动系统的可靠性计算可通过系统逻辑关系和数学关系来实现。该计算主要体现在可靠性框图的绘制与可靠度大小的计算方面。为了满足齿轮传动系统及子系统的可靠性定量要求,必须建立可靠性关系模型与可靠性数学模型。
笔者将以机械零件的可靠性建模为基础,分析不同类型和结构特点的机械传动系统可靠性建模方法;以功率分支齿轮传动系统为例,给出2种机械传动装置可靠性建模方法的适用范围。
机械零部件的可靠度计算是基于应力-强度分布干涉模型,零件的强度S和工作应力σ均为服从概率统计分布曲线的随机变量。
作为可靠性设计的基本原则,零部件的强度值要高于应力值。对于固定值而言,其可以从安全系数上得以体现;而对于离散化后的随机变量,往往并不能简单地用一个参数来表示。
在特定条件下,强度与应力两概率密度函数曲线发生了交叉,阴影部分称为干涉区。
基于应力分布和强度分布的干涉理论,可靠度作为强度大于应力的总概率之和,其表达式如下:
(1)
当应力为xσ时,强度S大于该应力值的概率表示如下:
(2)
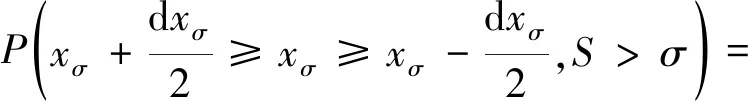
(3)
由此可知,在整个积分区间内,对应力σ进行积分,可得机械零部件的可靠度如下:
(4)
由于系统中不同零部件具有不同的功能,故各元素对系统的可靠性影响能力不同。通过分析对传动系统影响较大的系统元素,即可近似得到真实的系统可靠性数值。
实际上,大多数机械传动系统的可靠性模型应具有如下特征[16]:传动系统任何一个零件失效将导致系统发生失效;同一传动系统中,各零部件的失效既不会是独立事件,也不会是完全相关事件,即存在一定程度的相关关系。
若机械传动系统在广义随机载荷L的作用下运行,设载荷L的概率密度函数为fL(L),系统各零部件由此引起的应力Hi=Hi(L),fi(S)是第i个零件强度的概率密度函数,则在L=L0时,由式(4)可知零件的可靠度如下:
(5)
载荷L落在L0附近dL区间内的概率如下:
(6)
若各零件间关于强度Si是相互独立的,则各零件均可靠的概率如下:
(7)
假设载荷L与各零件的强度相互独立,对应于所有可能的L0,上述概率为系统的可靠度如下:
(8)
式(8)考虑了各零件关于载荷相关的系统可靠性干涉模型,根据式(7)及零件的可靠性干涉模型,系统可靠度计算公式如下:
(9)
由上述的推导可知,式(5)与式(9)在形式上存在明显的区别。式(8)仅代表了一种系统可靠性计算模型,在处理复杂系统时,由于存在相当繁琐的计算,故求解实际问题时并不常用。
2 基于可靠性建模的数字化软件
齿轮传动系统的可靠性建模是基于系统中各零部件间的故障逻辑关系,软件运用系统可靠性框图,表达系统的功能原理。笔者采用C#.NET,开发了一种基于普通概率法与蒙特卡洛模拟法的系统可靠性建模软件。
可靠性建模数字化分析流程如图1所示。
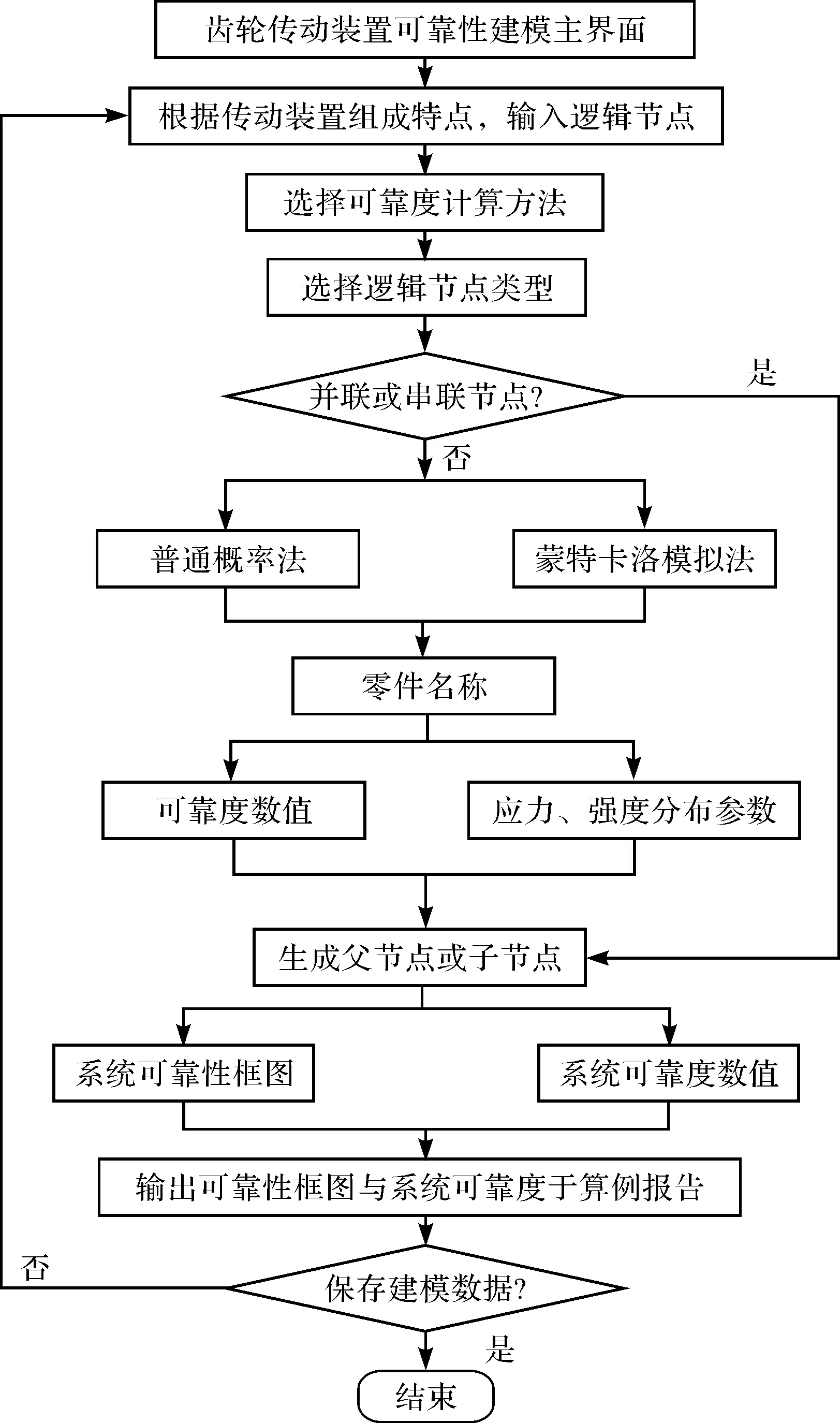
图1 可靠性建模数字化分析流程
在完成机械零部件可靠性建模参数的输入之后,结合树形结构控件中节点间的逻辑关系,笔者最终绘制出系统的可靠性框图。
可靠性关系模型输出界面如图2所示。
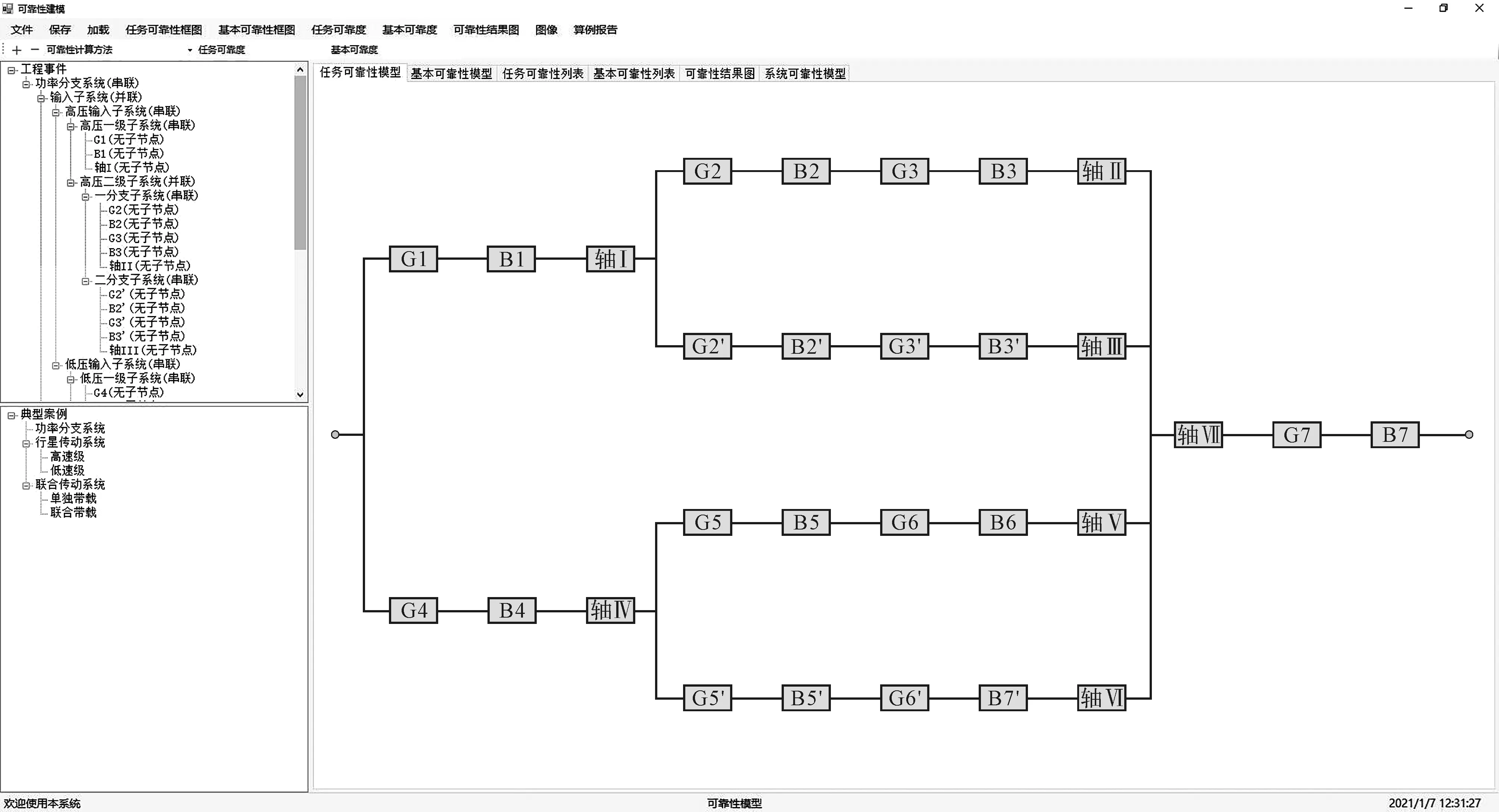
图2 可靠性关系模型输出界面
针对逻辑结构生成相应的基本可靠性框图和任务可靠性框图后,笔者设计通用算法,对用户输入的逻辑结构进行解析。
首先,需要判断结构的基本可靠性模型和任务可靠性模型是否一致,判断逻辑采用前序遍历算法,其条件为结构中是否存在并联关系节点。由于任务可靠性框图不简化混联结构,逻辑算法的关键在于对混联结构中并联结构的处理,需要计算结构中最大串联节点数。该函数对串联结构返回各子节点最大串联节点数之和,对并联结构返回子节点最大串联节点数。
设节点的最大串联节点数为g。g算式如下:
(10)
式中:i为g的第i个子节点;k为g有k个子节点。
式(10)为递归公式。按照递归循环方法设计函数,即可得到输入节点的最大串联节点数。
为了表征任务可靠性框图的逻辑信息,设第i个节点的位置信息为L。L算式如下:
Li=(xi,yi,wi)
(11)
式中:xi为第i个节点的横坐标;yi为第i个节点的纵坐标;wi为第i个节点的所属的纵向范围。
逻辑信息的计算顺序按照节点遍历顺序进行,该过程基于树的前序遍历。
其前序遍历算法流程如图3所示。

图3 前序遍历算法流程图
遍历全部节点的过程中,首先计算的初始值如下:
(12)
式中:Le为绘图区域的长度,像素密度单位,PPI;W为绘图区域的宽度,PPI;g0为根节点的最大串联节点数。
当节点i为串联节点,并且节点i+1为节点的第一个子节点时,L算式如下:
Li+1=Li
(13)
当节点i为并联节点,并且节点i+1为节点的第一个子节点时,L算式如下:
(14)
当节点i为串联节点,并且节点i+1为节点的领节点时,L算式如下:
Li+1=Li·E+(G,0,0)
(15)
当节点i为并联节点,并且节点i+1为节点的领节点时,L算式如下:
(16)
当节点i为串联节点,并且节点i+k为节点的领节点时,L算式如下:
Li+k=Li·E+(G·gi,0,0)
(17)
当节点i为并联节点,并且节点i+k为节点的领节点时,L算式如下:
(18)
遍历完毕全部零件节点后,笔者采用类以存储各节点的逻辑位置信息,从而实现类对象与零件节点一一对应目的。由于基本可靠性框图为全串联模型,故只需生成每一零部件的可靠性框图,依次排列后,即可完成该项建模任务。
然而传动系统的任务可靠性框图相对较复杂,需考虑串联、并联及混联结构的空间布局与节点间的位置关系,因此,需针对串联和并联节点,分别基于递归思想,借助式(13)~式(18)得到其各子节点的坐标值。
3 算例及结果分析
以功率分支齿轮传动系统为例,其功率分支齿轮传动装置结构如图4所示。
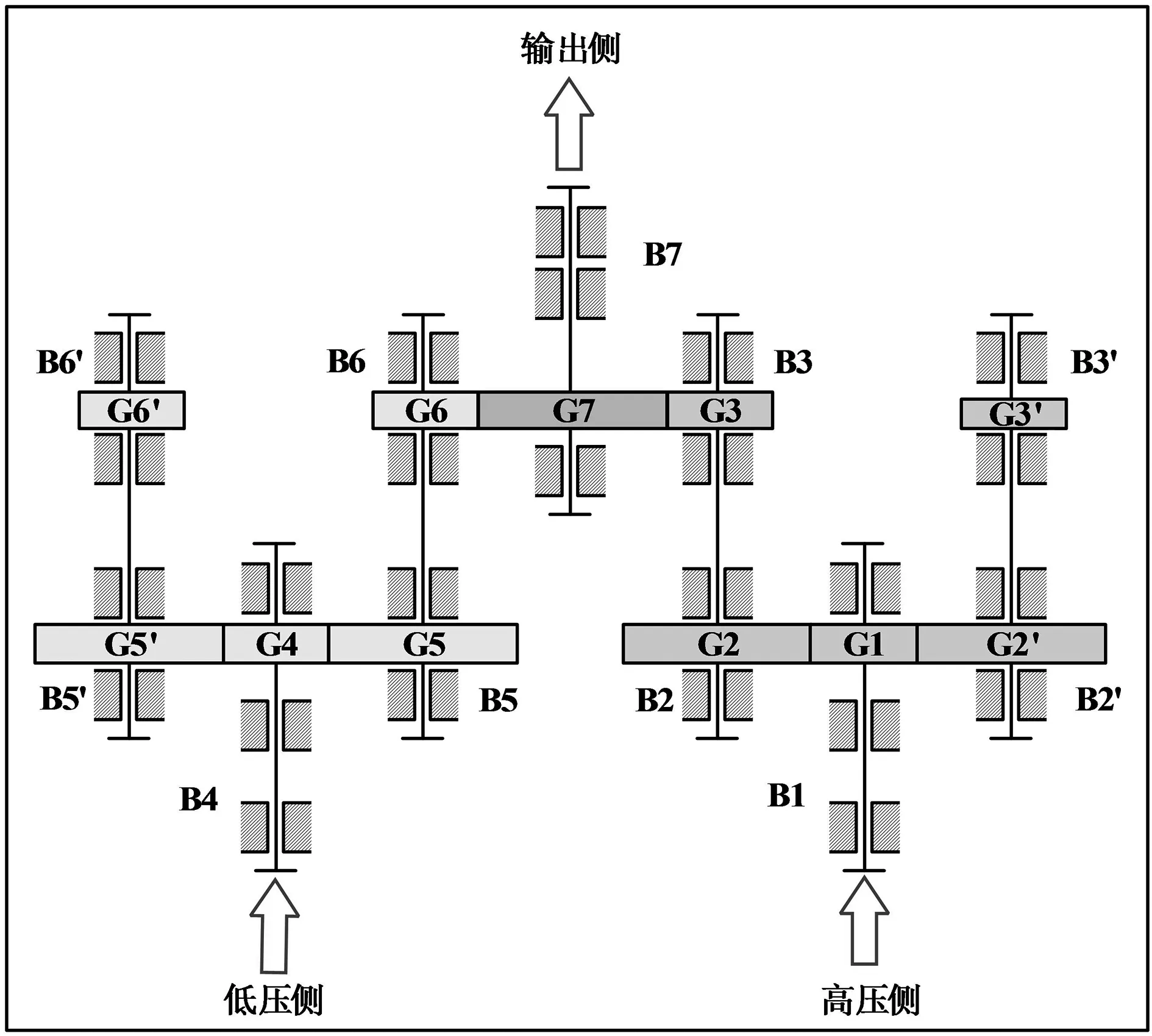
图4 功率分支齿轮传动装置结构图
笔者根据该齿轮传动系统的工作环境与所受载荷特点,建立其可靠性模型时只考虑齿轮、轴和轴承3类零件的影响。
由于零部件为单元串联结构,故可以得到系统的基本可靠性框图,如图5所示。
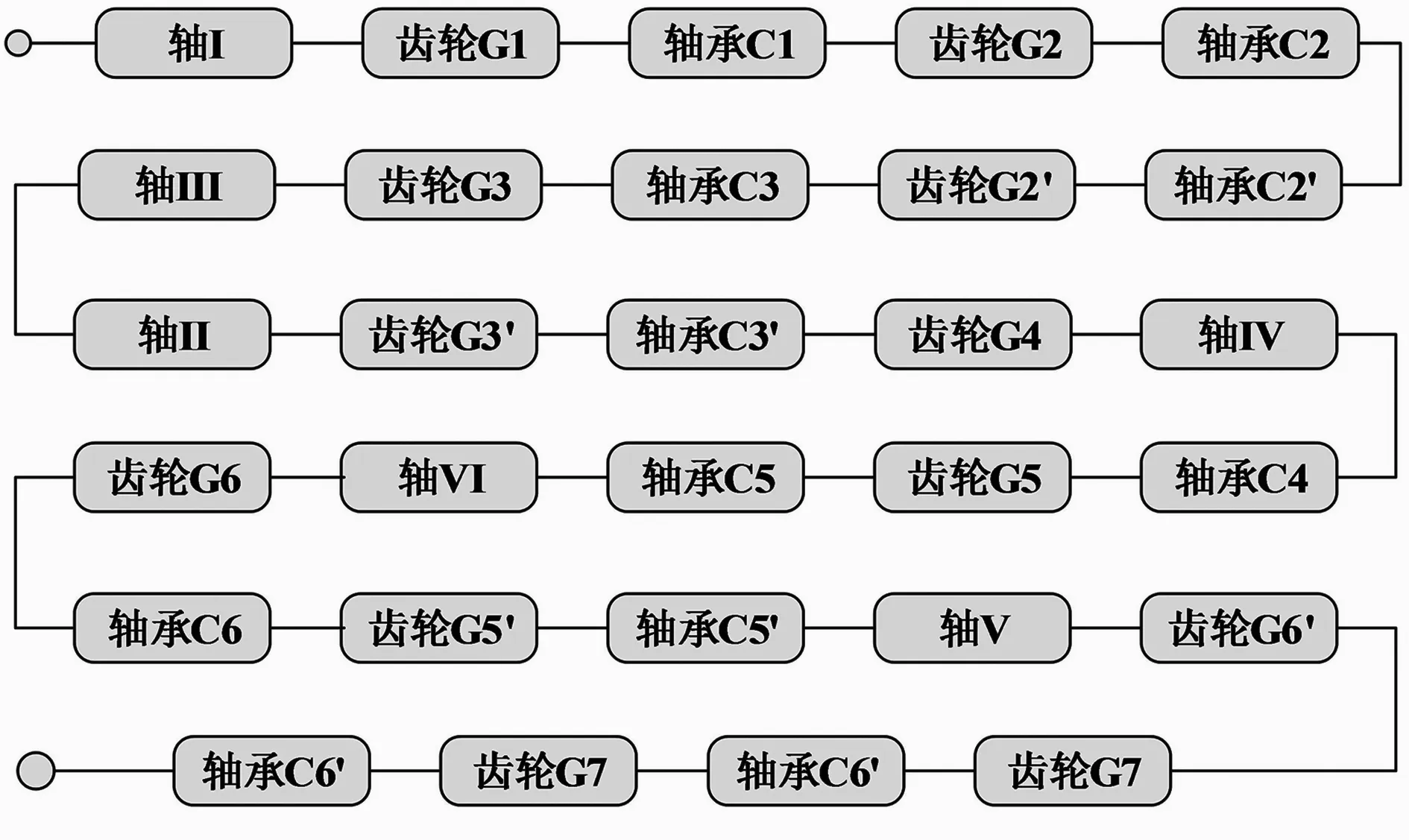
图5 系统基本可靠性框图
任务可靠性模型需根据传动系统的工作特点,结合系统各零部件所执行的功能,得出包含串、并联结构的任务可靠性框图。
系统任务可靠性框图如图6所示。

图6 系统任务可靠性框图
笔者参照非电子元器件可靠性数据手册(nonelectronic parts reliability data,NPRD)可靠性数据,得到各零部件的故障率,通过故障率与可靠度之间的转化关系求得可靠度,最后将可靠度代入公式中,进行计算。
由理论推导可得,故障率λ与可靠度R(t)的计算关系如下:
(19)
如果组成系统的零部件数目较多,并且存在明显的损耗性零件,对有限寿命已知的零件需要定期更换,则零件失效率λ可近似地认为是常数。
取工作时间为12 000 h,可得系统主要零部件失效率λ及可靠度如表1所示。

表1 统主要零部件失效率及可靠度
零件的可靠度可以采用蒙特卡洛模拟法得到。
蒙特卡洛模拟法模块通常是利用MATLAB软件,来模拟零件的可靠度计算过程。在进行模拟试验之前,需要明确机械零部件强度与应力的概率分布情况,建立其应力-强度干涉模型,然后方能求解其可靠度。
同一工况下,齿轮应力与强度的蒙特卡洛拟合数据散点图,如图7所示。
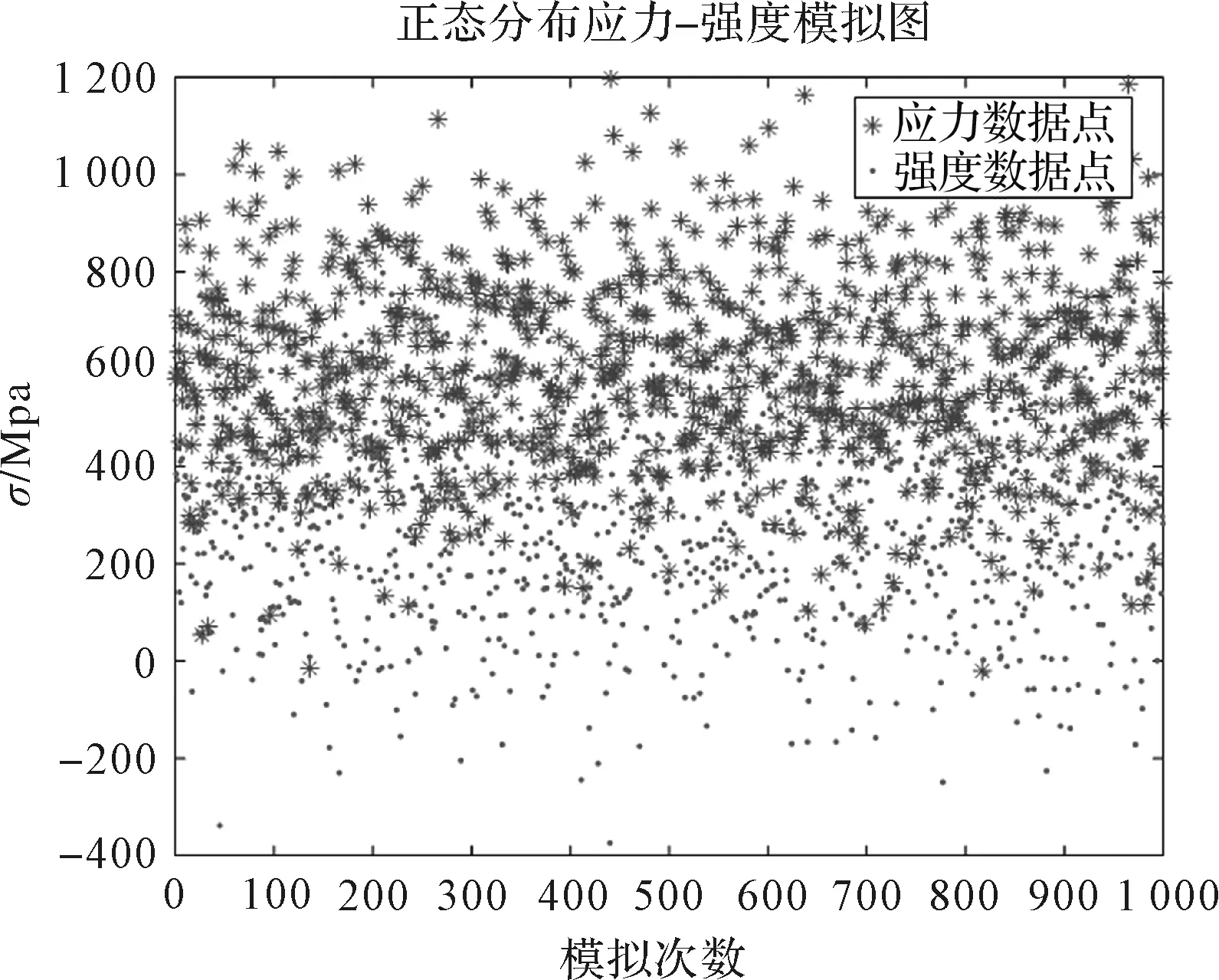
图7 齿轮应力及强度的蒙特卡洛拟合数据散点图
为了简化其运算过程,可根据系统的任务可靠性框图,将各分支路看成一个整体,而每一整体内部为串联结构。
由串联模型计算公式可得出各组成单元可靠度。
系统各单元可靠度如表2所示。

表2 系统各单元可靠度
由表2可得,该系统基本可靠性的可靠度:Rc=RA·RB·RC·RD·RE·RF·RG=0.834 4。
其中,设单元内部各零部件的可靠度为R1、R2。
最后,根据任务可靠性模型的计算特点,可得该系统的任务可靠度数值:Rb=RG·(RA·RH+RB·RI-RA·RB·RH·RI)=0.981 8。
因此,运用普通概率法,计算得到该功率四分支传动系统的基本可靠度为0.834 4,任务可靠度为0.981 8。
齿轮传动系统基本可靠度取决于各个环节的可靠度。若想提高系统的基本可靠度,需要采取有利于增加零部件自身可靠度的措施。
软件生成基本可靠性与任务可靠性对比,如图8所示(解析计算结果与软件计算结果误差为0.016%)。
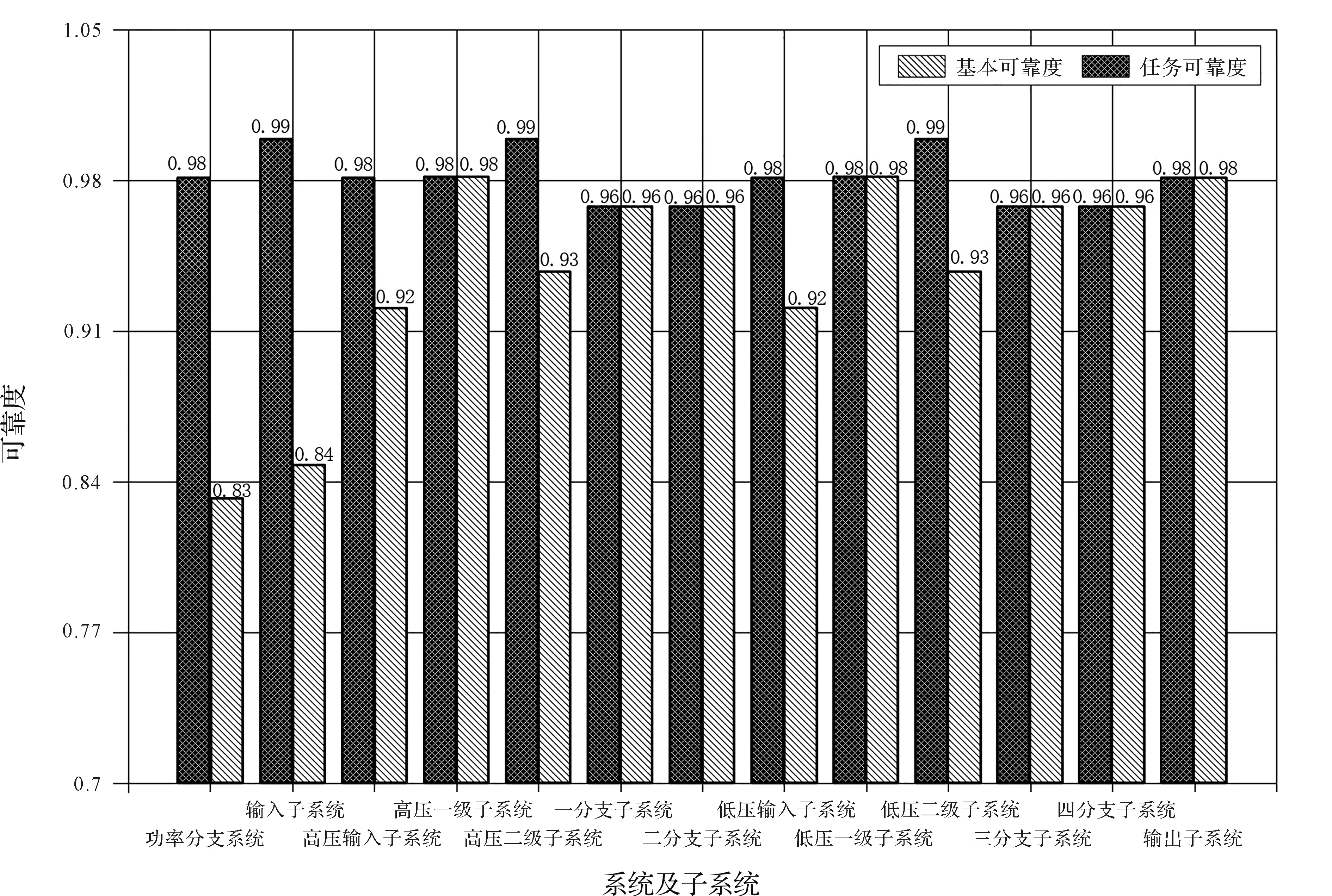
图8 基本与任务可靠性结果对比图
通过各子系统与系统的对比可得:随着系统并联部分的增多,基本可靠度与任务可靠性之间的差值会越来越大。因此,在可靠性设计中,可通过该图快速判断冗余系统的位置,为系统的合理设计提供支持。
为了验证该可靠性数字化分析方法及软件的正确性,笔者同时采用解析法进行了计算,两者取得了较好的一致性。
4 结束语
针对复杂机械系统可靠性建模计算量大和耗时长等问题,综合应力-强度干涉模型和载荷相关性,笔者提出了一种齿轮传动系统可靠性快速建模的数字化分析方法,建立了考虑各个零件载荷相关性的系统可靠性模型,设计了齿轮传动系统可靠性快速建模的数字化平台;最后,以功率分支齿轮传动系统为例,采用解析法和数字化软件,对其进行可靠性建模与分析,对可靠性快速建模数字化分析平台的有效性进行验证。
研究结论如下:
1)笔者建立了基于零件载荷相关性的齿轮传动系统可靠性模型,研究了齿轮传动系统可靠性关系模型,推导了基本可靠性和任务可靠性数学模型,实现了根据实际齿轮传动结构选用混联模型表征可靠性关系模型的目的;采用数理统计概率法,对可靠性数学模型进行了求解,得到了系统基本可靠度为0.834 4,任务可靠度为0.981 8,提高了系统可靠性建模精度;
2)开发了齿轮传动系统数字化分析平台可靠性建模模块,在前处理部分实现了输入模型结构参数;在中间处理部分根据逻辑结构和递归思想,采用遍历模型,计算了可靠性模型框图参数,采用蒙特卡洛法计算了可靠度;在后处理模块实现了自动生成基本可靠性及任务可靠性模型框图、系统可靠性结果表格、可靠性结果对比图和自动输出可靠性建模分析报告Word文档目标,提高了系统可靠性建模效率;
3)基于所开发的齿轮传动系统数字化分析软件可靠性建模模块,对功率分支齿轮传动系统进行了可靠性建模数字化分析,软件仿真分析结果与解析计算结果取得了较好的一致性,验证了笔者所提出的可靠性建模数字化分析方法(及软件)的可行性和正确性。
通过对高速重载齿轮传动系统的研究,笔者发现系统可靠性模型与许多因素有关。因此,在后续的研究过程中,笔者将采用多场耦合方法,以此来综合研究齿轮传动系统可靠性建模的数字化设计。
