基于协整分析与改进潜结构投影的质量相关故障检测

王晓兵, 郑海文, 孔祥玉

(1.陆军炮兵防空兵学院郑州校区,郑州 450000; 2.火箭军工程大学,西安 710000)

0 引言

随着传感器和计算机技术的迅速发展,复杂装备的过程数据变得信息量丰富且获取便捷,从而有力推动了基于数据驱动的过程监测方法的发展。过程监测技术是保障重大装备和复杂工业生产过程安全工作和保证生产质量的关键技术。其中,利用多元统计过程监测(Multivariate Statistical Process Monitoring,MSPM)[1-2]的方式对高维数据进行处理时表现出模型简单且易于实现等优势。常用的MSPM投影方法有主成分分析[3-4],偏最小二乘(Partial Least Squares,PLS)[5],Fisher判别分析[6]和独立主成分分析[7]等。

PLS通过建立过程变量和质量变量之间的关系模型,对大型装备系统及复杂工业过程的输出质量和过程运行状态进行监测。但是PLS在质量相关故障检测过程中存在斜交分解,在提取特征过程中存在局限性[8]。为了更清晰地表述输入空间的相关信息,文献[9]提出一种全潜结构投影(Total Projection to Latent Structures,TPLS)的后处理算法,将得分和负载矩阵进一步分解;文献[10]提出了并行潜结构投影算法,该算法是将TPLS空间简明地划分为两个过程,即输入相关以及输出相关的结构;文献[11]提出改进的潜结构投影(Modified Projection to Latent Structures,MPLS),采用奇异值分解(SVD)进行空间分解,实现正交投影的同时,避免了大量的迭代过程。但MPLS进行监测时是基于过程平稳这一假设的,并不适合非平稳过程的质量相关故障检测,忽略非平稳变量的影响,很容易让故障信号隐藏在其变化趋势中。如果不考虑这种非平稳特征,所建立的模型将含有非平稳的随机趋势,会降低模型的准确性,难以满足高精度故障检测需求。为了描述非平稳变量之间的关系,协整分析模型可完成非平稳变量到平稳残差序列的转化,在共同趋势上体现出一种平稳的长期动态均衡关系[12]。为了精确地表征平稳变量和非平稳变量间的关系,需准确建立过程变量和质量变量的模型。

本文结合协整分析及改进潜结构投影(Cointegration Analysis and Modified Projection to Latent Structures,CA-MPLS)技术,提出一种新型质量相关故障检测方法。该方法首先基于非平稳变量构建协整模型,获取到平稳的残差序列;其次,完成对平稳残差序列以及平稳变量数据二者的融合,引入SVD分解完成正交投影空间的构建,实现融合数据到质量相关及质量无关两个子空间的有效投影;最后,分别设定两个子空间对应统计指标实现在线故障检测,通过田纳西-伊斯曼(Tennessee Eastman,TE)过程完成了本文方法的可行性验证。

1 协整分析

协整分析[13]是一种有效地描述非平稳变量间关系的方法,可实现时间序列分析中短期和长期模型优势的有力结合。

假设存在非平稳时间序列,记作wt,历经d次差分处理,形成平稳时间序列,那么称之为d阶单整时间序列,记为wt-I(d)。文献[14]形成的协整分析理论表示非平稳时间序列的线性组合可以是平稳的。针对非平稳变量z∈Rm,存在一个向量βi∈Rm,使得其线性组合为平稳过程,可以描述为

(1)

式中,γi是平稳的残差序列。

文献[15]提出一种基于向量自回归(Vector Auto Regressive,VAR)模型的方法来完成协整向量的求取。给定X(N×m)=[x1,x2,…,xm],xt=[x1,x2,…,xN]Τ是非平稳时间序列,假设xt-I(1),即时间序列均是同阶单整的,其中,N为样本数,m为非平稳变量数。建立VAR模型为

xt=Π1xt-1+…+Πpxt-p+c+μt

(2)

式中:Πi为系数矩阵;μt为白噪声向量;c为常数向量;p为所建模型对应阶次。

在式(2)两端减去xt-1,得到误差纠正模型为

(3)

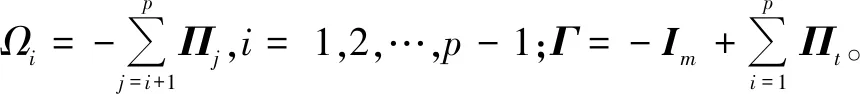
Γ可以分解为A和β两个列满秩矩阵,即

Γ=AβΤ

(4)

式中:A∈Rm×r;β∈Rm×r。

由此式(3)可以转化为

(5)

根据式(5),可以得到残差序列γt-1为

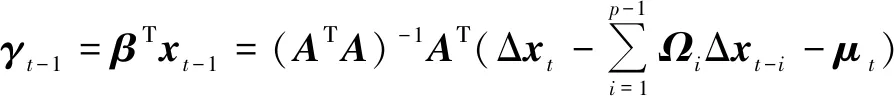
(6)

由于xt为一阶单整的,Δxt和Δxt-1为平稳的,则式(6)右边为平稳的,即其线性组合βΤxt-1中各元素均为平稳的。因此,矩阵β=[β1,β2,…,βr]∈Rm×r中各列被看作协整向量。

文献[15]提出一种检验方法用于确定协整向量数。假设向量数为r(1≤r≤m-1),协整向量βi(i=1,…,r)间线性无关,则z经过协整后的秩为r。在z变量间提取的协整关系可以由r个残差序列表示。根据Johansen理论得到协整矩阵为β=[β1,β2,…,βr]∈Rm×r,协整模型为

(7)

式中,γti为平稳的残差序列。

2 基于CA-MPLS的质量相关故障检测方法

MPLS对质量相关故障进行检测时是基于过程平稳这一假设的,并不适合非平稳过程的质量相关故障检测。协整是变量间的线性组合,能够消除非平稳变量的随机趋势。基于上述情况,通过协整分析与MPLS相结合的方式,提出一种新型质量相关故障检测方法,综合利用平稳变量和非平稳变量的特征信息,建立检测模型,实现在线监测。

2.1 模型建立

在大型装备及复杂工业过程中,并不是所有的过程变量都具有非平稳性,而平稳变量的存在会对协整模型造成影响,使其不能准确地描述非平稳变量间长期均衡的关系[15]。因此,在进行协整分析前应该将非平稳变量与平稳变量隔离开,常用ADF(Augmented Dickey-Fuller)检验[14]的方法来判断变量是否非平稳。给出一组正常工况下输入数据矩阵X=[x1,x2,…,xm]∈RN×m和输出数据矩阵Y=[y1,y2,…,yp]∈RN×p,采用ADF检验的方式划分过程变量,即非平稳变量和平稳变量,记为

(8)

式中:Xu和Xs分别对应非平稳变量和平稳变量矩阵;N为样本数;ν为非平稳变量数;h为平稳变量数。

对于选择出来的非平稳变量Xu,根据协整分析建立模型

γu=Xuβ

(9)

式中,γu∈RN×r,为平稳残差序列;β∈Rν×r,为协整向量,r为协整向量数,由Johansen检验[15]确定。

将γu与变量Xs二者融合增广为矩阵Xc,作为新的输入数据,即

Xc=[γu,Xs]。

(10)

矩阵Xc表征了输入数据所含的所有平稳特征,克服了非平稳随机趋势对模型准确度的干扰[16]。利用MPLS对Xc正交分解,可有效避免无用信息对输出预测的干扰。建立Xc∈RN×(r+h)与输出数据Yc∈RN×P之间的MPLS模型,有如下关系

(11)

(12)

对ΨΨΤ进行SVD分解

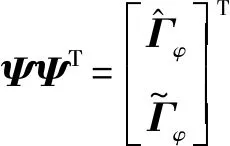
(13)

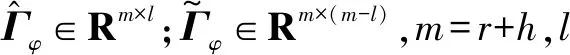
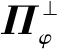
(14)

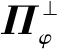
(15)

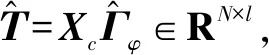
最终可得到Xc∈RN×(r+h)与Yc∈RN×p的MPLS模型[11]为

(16)

2.2 在线故障检测

给出一个新的观测数据xnew,根据2.1节ADF划分过程将xnew分为两部分,即非平稳变量xun和平稳变量xsn,然后对xun协整,得到平稳的残差序列γun。依据式(10)得到增广数据xcn,由式(7)计算融合数据分别在质量相关子空间和质量无关子空间的得分向量,即

(17)

(18)

依据两项指标获取检测过程是否存在故障。

利用χ2分布[11]计算相应的控制限

(19)

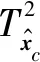
2.3 基于CA-MPLS的故障检测流程

CA-MPLS方法监控过程分为离线建模和在线监控两部分,图1为基于CA-MPLS的故障检测流程图。详细步骤描述如下。

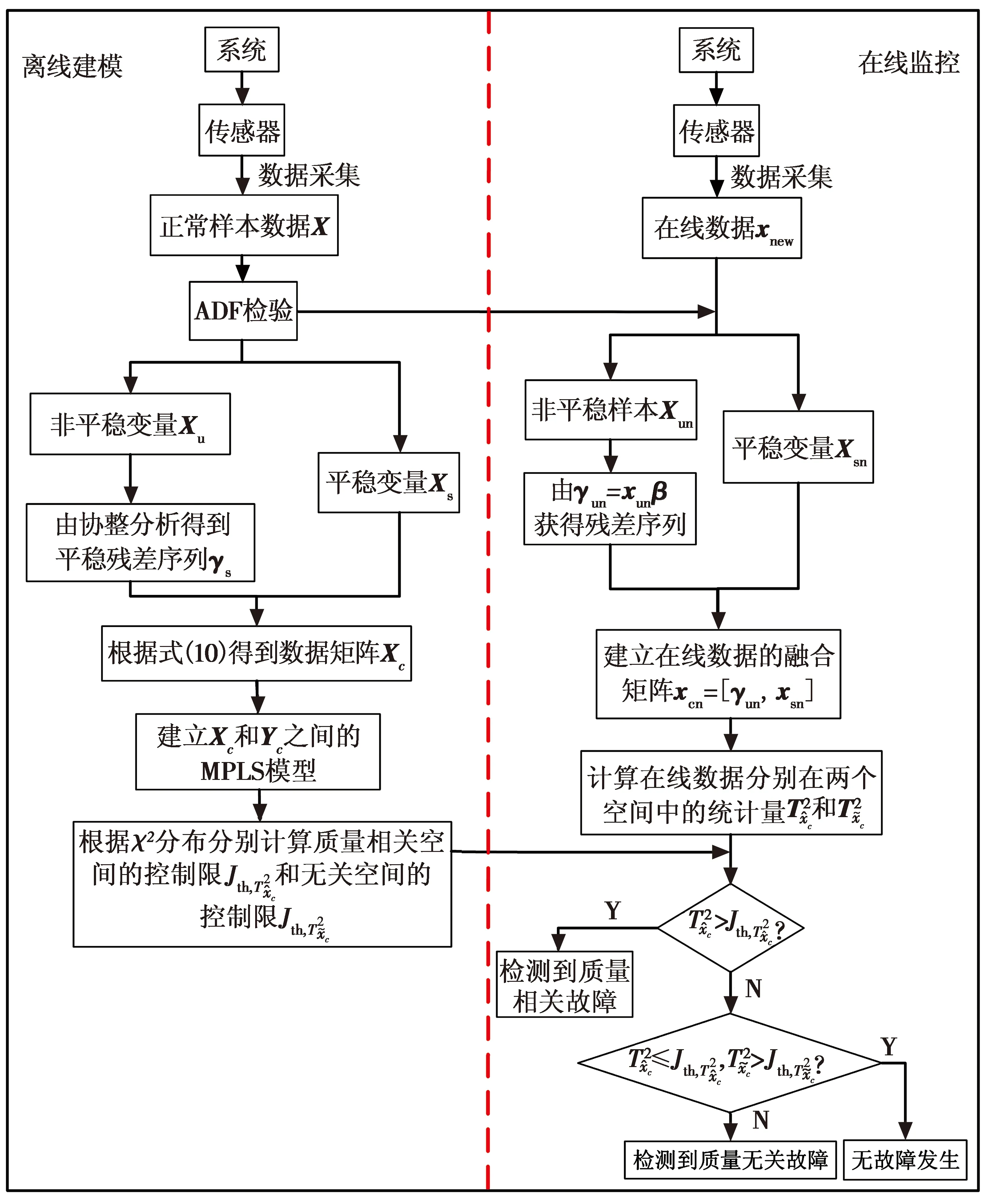
图1 基于CA-MPLS故障检测流程图

1) 离线建模阶段。

① 对X进行ADF检验,将其划分为非平稳变量Xu和平稳变量Xs。

② 根据2.1节协整分析相关理论确定协整向量β。

③ 建立非平稳变量Xu的协整模型,根据式(9)提取出平稳的特征信息γu。

④ 根据式(10)建立融合数据矩阵Xc。

⑤ 求Xc与输出数据Yc之间的系数矩阵ψ。

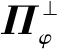
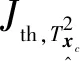
2) 在线监控阶段。

① 将每个新来的测试样本xnew分为平稳样本xsn和非平稳样本xun。

② 利用协整模型获得非平稳变量xun的残差序列γun。

③ 将γun和xsn融合得到xcn。

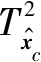
3 仿真实验

本节选取TE过程展开仿真,通过比较MPLS[11],CA-SRS和CA-MPLS这3种方法的检测性能,验证本文方法的可行性和有效性。参考如下两项技术指标进行验证,即故障检测率(FDR)和故障误报率(FAR)[8]

(20)

式中:Nnea为有效报警数;Nnfa为误报警数;Ntfs为故障样本总数。

在实际工业过程中,较好的质量相关故障检测方案通常呈现以下两个特点:1) 存在质量相关故障时,指标FDR趋高;2) 存在质量无关故障时,指标FAR趋低。

TE过程是由美国伊斯曼化学公司基于实际工业过程提出的仿真实例,已经被广泛作为连续过程检测、诊断、监控等方法的研究平台[15-16]。该过程模型包含冷凝器、气液分离器、循环压缩机、反应器和汽提塔5个操作单元。DOWNS和VOGEL对TE过程的详细描述参见文献[6]。

本文实验选取过程变量X,由测量变量XMEAS(1-22)和操纵变量XMV(1-11)组成, XMEAS(35)作为质量变量Y,采样时间间隔为3 min。根据文献[9],引入数据集IDV(1),(2),(5),(6),(8),(10),(12),(13)表征TE过程发生质量相关故障,数据集IDV(3),(4),(9),(11),(15)则表征发生质量无关故障。本文采用500个正常样本建立MPLS[16],CA-SRS[11]和CA-MPLS模型,分别对质量相关故障数据和质量无关故障数据进行测试。假定故障数据含960个样本,划定数据包中前160个为正常样本,后800个为故障数据。根据Johansen检验[15]确定CA-SRS和CA-MPLS协整向量个数r=6。

采用MPLS和CA-MPLS两种方法对质量相关故障IDV(10)进行检测,结果分别如图2和图3所示。

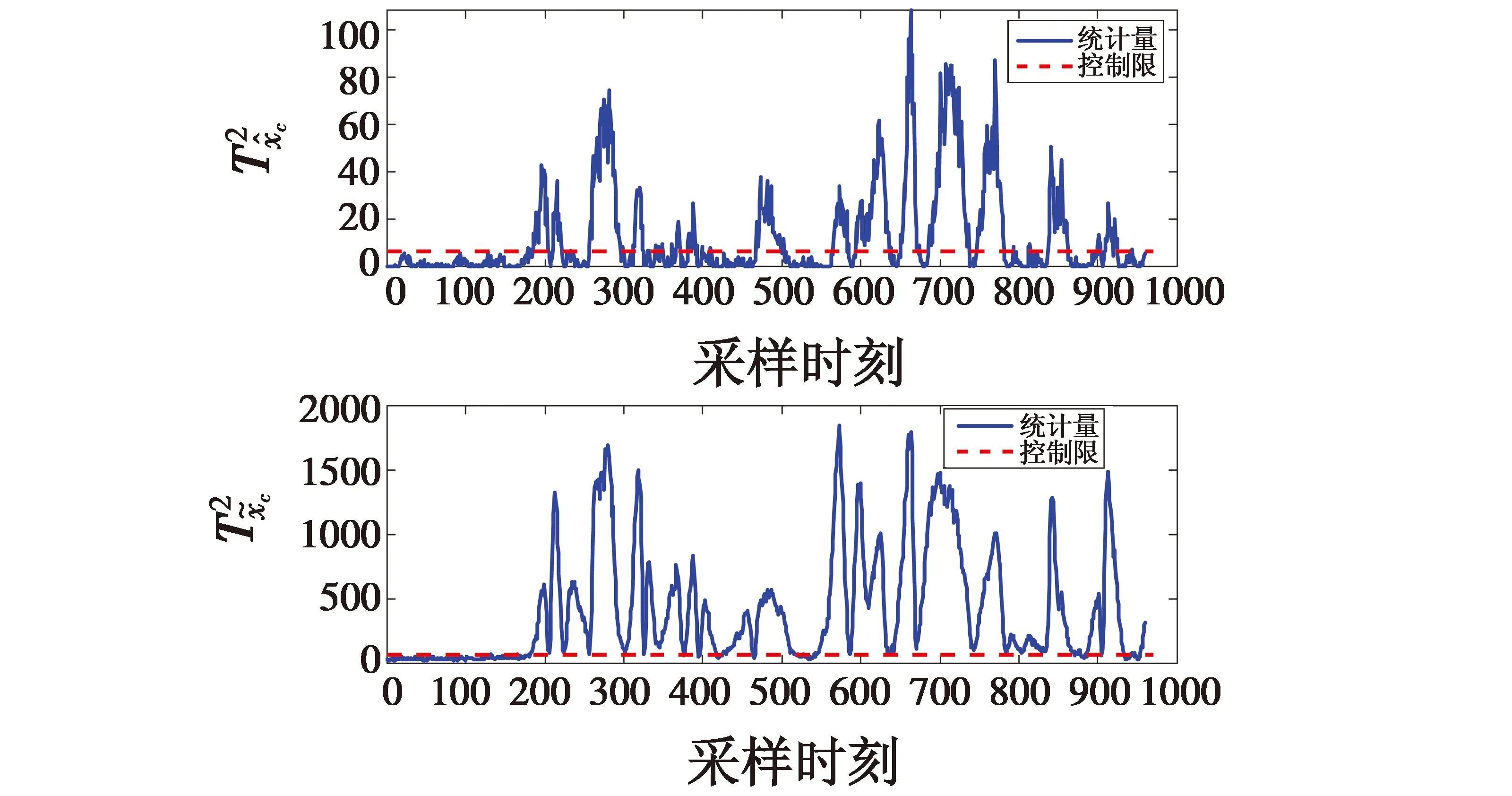
图2 MPLS作用于IDV(10)的故障检测结果

图3 CA-MPLS作用于IDV(10)的故障检测结果

采用MPLS,CA-MPLS两种方法对质量无关故障IDV(4)进行检测,结果如图4和图5所示。该故障是由反应器冷凝水入口温度发生阶跃变化引起的,反应器温度是通过级联控制器控制的,这种变化不会影响产品质量。在该类故障发生时,操作人员更希望质量相关的统计指标FAR低。

图4 MPLS作用于IDV(4)的故障检测结果

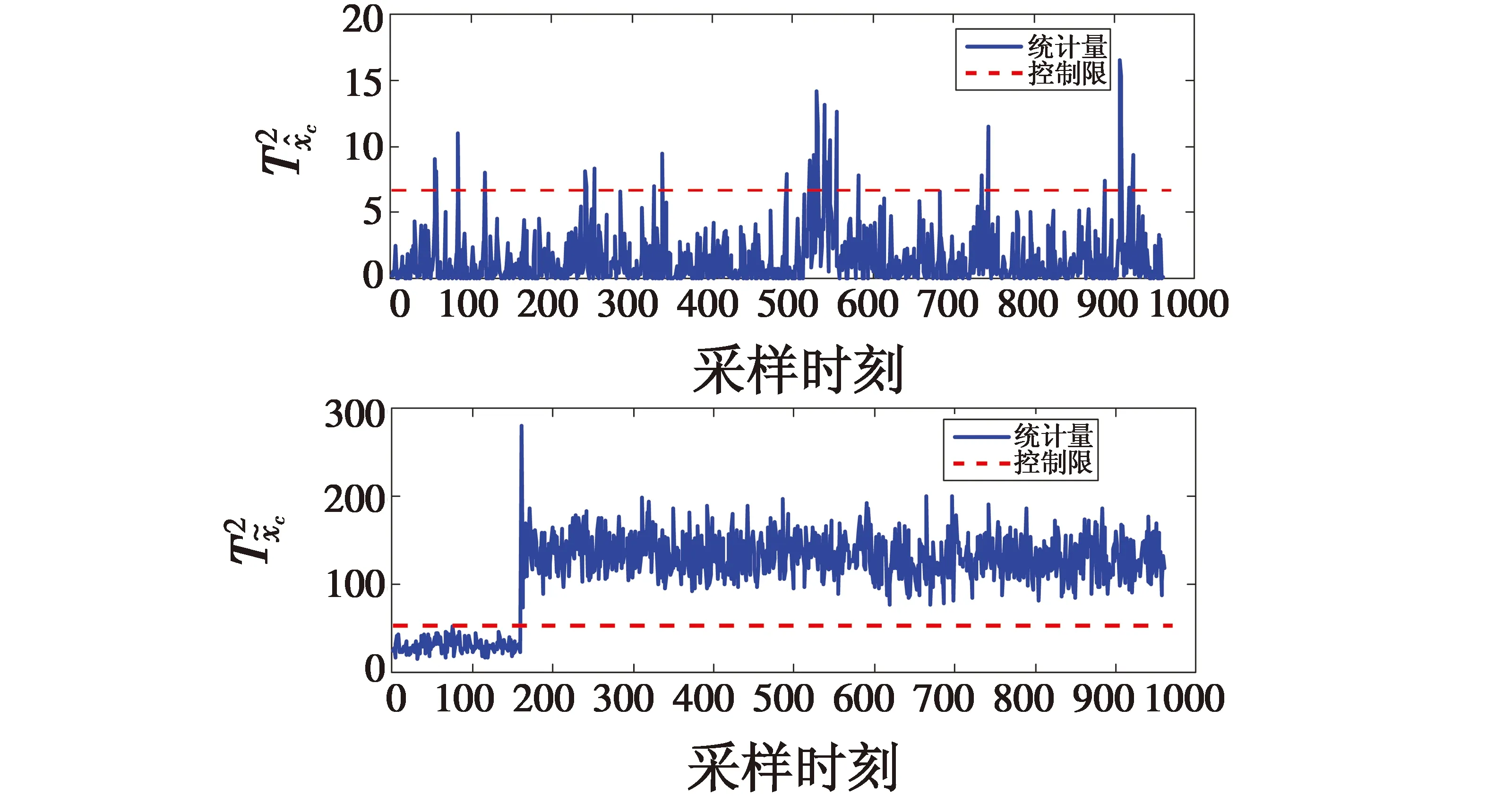
图5 CA-MPLS作用于IDV(4)的故障检测结果

采用CA-SRS方法对质量相关故障IDV(10)和质量无关故障IDV(4)进行检测,结果如图6所示。

图6 CA-SRS对质量相关故障IDV(10)和质量无关故障IDV(4)的检测结果

由图6可知,CA-SRS能有效检测到与质量相关的故障,然而对于与质量无关的故障,CA-SRS无法检测,这是由于其在建模过程中只考虑了非平稳变量,使得故障信息丢失,同时,CA-SRS方法本身只有一个监控指标用于故障检测,无法有效区分故障是否与质量相关。而本文所提方法综合利用了非平稳和平稳变量信息,避免了信息丢失对模型精度的影响,能够有效检测到质量相关和质量无关故障。

表1列出了CA-SRS,MPLS和CA-MPLS这3种方法对TE过程中质量相关故障IDV(1),(2),(5),(6),(8),(10),(12),(13)的检测结果,其中,加黑数据为3种方法中检测率较高的数据。

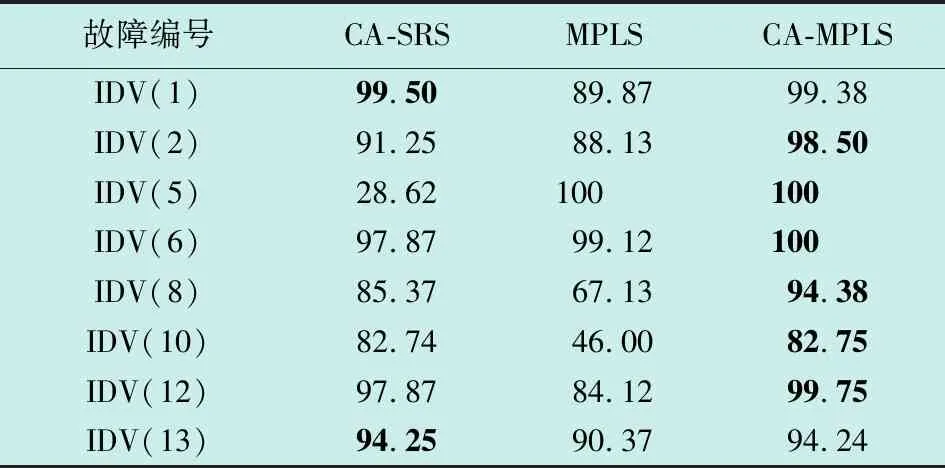
表1 TE过程中质量相关故障的故障检测率(PDR)

由表1可以看出,与CA-SRS相比,只有在IDV(1)和IDV(13)的情况下,CA-SRS的质量相关故障检测率略高于本文方法,在其他情况下,本文方法的检测效果均优于CA-SRS且对质量相关故障IDV(5)和IDV(8)的检测率有大幅度提高。与MPLS相比,本文方法的质量相关故障检测率有了全面提高,其中,对IDV(1),IDV(2),IDV(8),IDV(10),IDV(12)的检测率分别提高了9.51个百分点,10.37个百分点,27.25个百分点,36.75个百分点和15.63个百分点。

质量无关故障在确保不影响产品质量的前提下,应尽量不报警,减少停机检修频次,最大限度保证产品质量。由于CA-SRS不能区分质量相关故障与质量无关故障,无法判断是否质量相关和质量无关,不再讨论相应的误报率。表2罗列了质量无关故障作用于质量相关空间时,MPLS与CA-MPLS检测的误报率,其中,加黑数据为MPLS和CA-MPLS两种方法中误报率较低的数据。由对比结果可知,本文方法对IDV(3),IDV(4),IDV(9),IDV(11),IDV(15)的误报率分别降低了9.62个百分点,8.25个百分点,4.25个百分点,4.37个百分点和5.51个百分点。

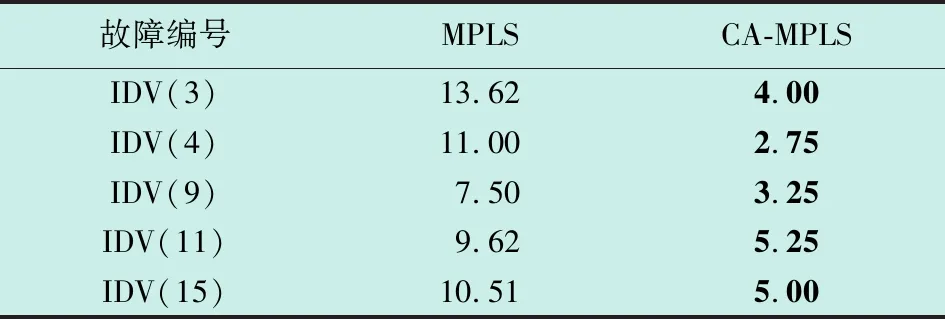
表2 TE过程中质量无关故障误报率(FAR)

4 结论

本文提出一种基于CA-MPLS的质量相关故障检测方法。结合协整分析的优势提取非平稳变量间的平稳特征信息,去除非平稳变量随机趋势对模型精度的影响,并在建立模型时尽可能保留质量相关的关键信息。TE过程实验表明,本文方法比MPLS具有更好的质量相关故障检测性能,成功提升了质量相关故障检测的准确率,同时降低了质量无关故障误报的概率。