基于FFT插值的Keystone变换实现方法

张 亮, 杜庆磊, 胡 冰, 周必雷, 王安乐

(空军预警学院预警技术系,武汉 430000)

0 引言

雷达作为获取目标位置信息的传感器,在战场指挥引导、态势感知、武器制导等领域应用广泛。雷达信号处理中,经常面临目标跨距离门、损失信噪比(SNR)问题[1],特别是目标高速机动或雷达处于长时间相参积累模式时。Keystone变换(KT)是一种经典的雷达目标距离走动校正工具,适用于脉冲多普勒、捷变频、合成孔径等多种雷达体制[2-7]。KT实现过程包含2个关键环节[8-10],即模糊数补偿和回波慢时间去耦合。第1个环节涉及真实模糊数估计问题,通常根据积累后的目标峰值,采取循环搜索取极大值的方法得到;第2个环节涉及“构造虚拟慢时间”,通常采取对快时间频率单元回波进行时间尺度(TS)实现。所谓TS,即连续信号到其尺度版本的映射过程,通俗地讲,TS是一种对信号进行某种程度拉伸或者压缩的操作,由于TS数值计算方法有多种,现有KT实现方法研究主要围绕该问题展开。文献[8]最早提出基于辛格插值的TS计算方法,由于使用了时域内插函数,计算复杂度较高;为降低算法计算复杂度,文献[9]提出基于Chirp滤波的TS计算方法,但为实现1个快时间频率单元回波去耦合需要进行2次Chirp乘积、2次Chirp卷积,计算量同样较大;为降低算法计算量,文献[10]进一步提出基于“CZT+IFFT”的计算方法,其中,CZT为Chirp-Z变换(Chirp-Z Transform),IFFT为快速傅里叶逆变换(Inverse Fast Fourier Transform),该方法为实现1个快时间频率单元回波去耦合需要进行2次Chirp乘积、1次Chirp卷积和1次IFFT,计算量较文献[9]低,但由于回波距离门数量通常很大,算法整体计算量同样不容乐观。TS会导致信号带宽的变化,当TS后信号带宽增大时需要通过插值提升采样频率,而文献[10]缺乏该操作,去耦过程中容易出现频谱混叠,影响KT抗噪效能。另外,还有“DFT+IFFT”方法,DFT为离散傅里叶变换(Discrete Fourier Transform),计算过程与“CZT+IFFT”方法相同[11]。综上可知,现有KT实现方法在计算量和抗噪效能方面还不够理想,存在一定的改进空间。考虑到,辛格插值只是诸多插值算法中的一种,此外还有线性插值、高斯插值、FFT插值、三次样条插值和变换域插值等[12],寻找一种低计算量的插值算法,结合时域截取、补零等操作完全可以解决TS的快速计算问题,降低KT整体计算量。

基于上述分析,提出一种基于快速傅里叶变换(FFT)插值的KT实现方法,利用FFT插值算法解决KT去耦合问题。KT中TS要求非整数倍插值,如果采取“整数倍插值—抽取”的方式实现,计算量同样不容乐观。针对该问题,本文分析了FFT插值算法频域补零个数对插值后序列的影响,给出非整数倍插值的高效计算方法,并进行了举例说明。

1 Keystone变换基本原理

设雷达载频为f0,发射信号为线性调频脉冲信号,脉宽为Tp,带宽为B,调频斜率为ρ=B/Tp,雷达探测范围内1个点目标向站飞行,初始距离为R0,径向速度为vt。设目标反射系数为1,脉压后的目标回波为[8-11]

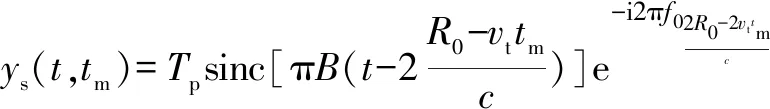
(1)

式中:t为快时间;tm=mTr,为慢时间,m=0,1,2,…,M-1,M为相参积累个数,Tr为脉冲重复周期;c为光速。利用KT进行目标距离走动校正,具体包含以下4步。

1) 步骤1。对脉压后回波沿快时间做傅里叶变换,得到

(2)

式中:f为快时间频率;fd为不模糊多普勒频率;F为模糊数;fr=1/Tr,为脉冲重复频率。

2) 步骤2。对ys(f,tm)沿慢时间进行模糊数补偿,得到

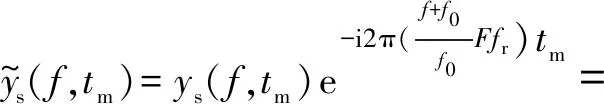
(3)

3) 步骤3。构造“虚拟”慢时间tom=[(f+f0)/f0]tm,代入式(3),去除f与tm的耦合关系,得到

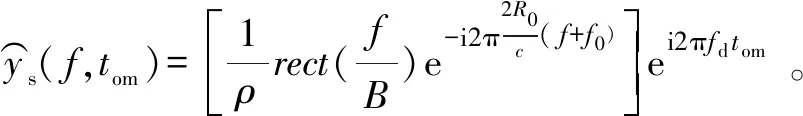
(4)

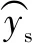
(5)

对式(5)沿tom进行FFT可实现相参积累。步骤2涉及模糊数估计问题,通常根据相参积累后的目标最大峰值搜索确定。对于宽带雷达,目标为多散射点模型,KT实现环节相同[13-14]。

2 理想与实际去耦合过程

KT包含2个重要环节,即模糊数补偿和去耦合,其中,第2个环节最为关键,现有研究多强调构造“虚拟”慢时间,该阐述较为模糊。为深入理解KT去耦合过程,将式(3)表示为

(6)

式中:φ(f)为快时间频率项;φ(αf,tm)为耦合项,αf=(f+f0)/f0,为频率尺度因子,对于雷达方αf是已知的。φ(αf,tm)可视为不同频率的复指数信号,频率为αffd,而KT去耦合本质是利用已知的αf,将αf≠1时的φ(αf,tm)映射为φ(1,tm)。如果不模糊多普勒频率fd已知,对φ(αf,tm)移频处理,可将αf≠1时的φ(αf,tm)调整为φ(1,tm),即

φ(1,tm)=φ(αf,tm)ei2π[(1-αf)fd]tm。

(7)

当fd未知时,需采取时间尺度(TS)的方法去耦合[9]。所谓TS,即连续信号x(t)到y(t)的映射过程[15],可表示为

(8)

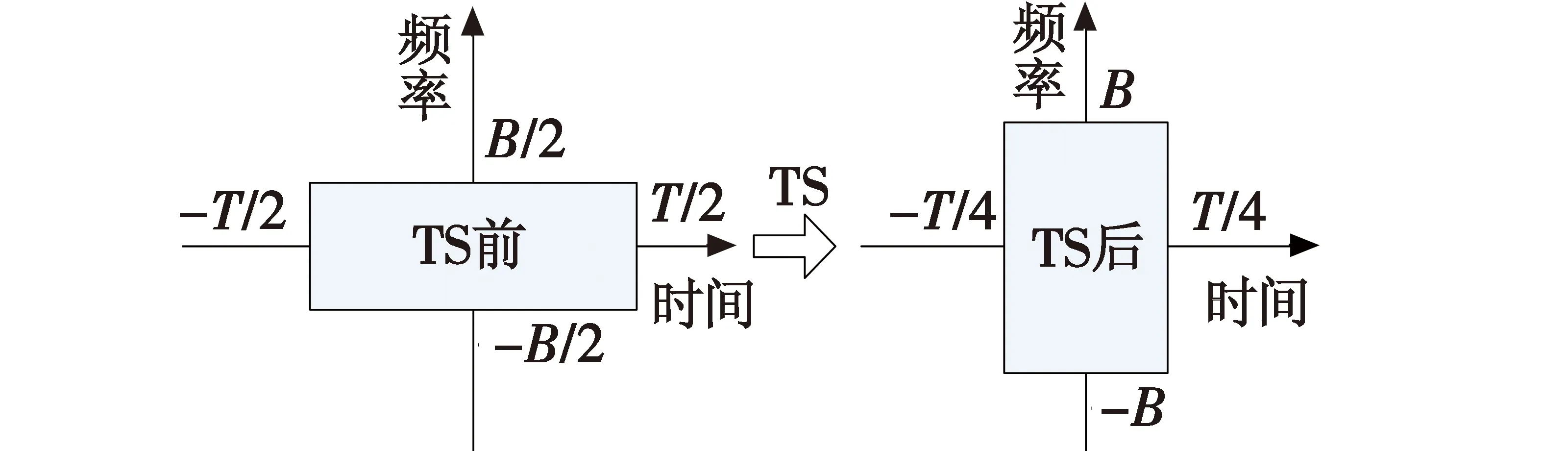
图1 TS前、后信号时频分布示意图

假设φ(αf,tm)为慢时间的连续信号,令α=1/αf,x(t)=φ(αf,tm),代入式(8)可得

(9)

由式(9)可知,TS操作可将φ(αf,tm)映射为φ(1,tm)实现去耦合。设αf为0.5,1.0和2,相参积累个数为16,图2为实际的去耦合过程示意图。当αf为0.5时,尺度因子α为2,TS后信号长度为TS前信号的1/2,当αf为2时,尺度因子α为0.5,TS后信号长度为TS前信号的2倍。

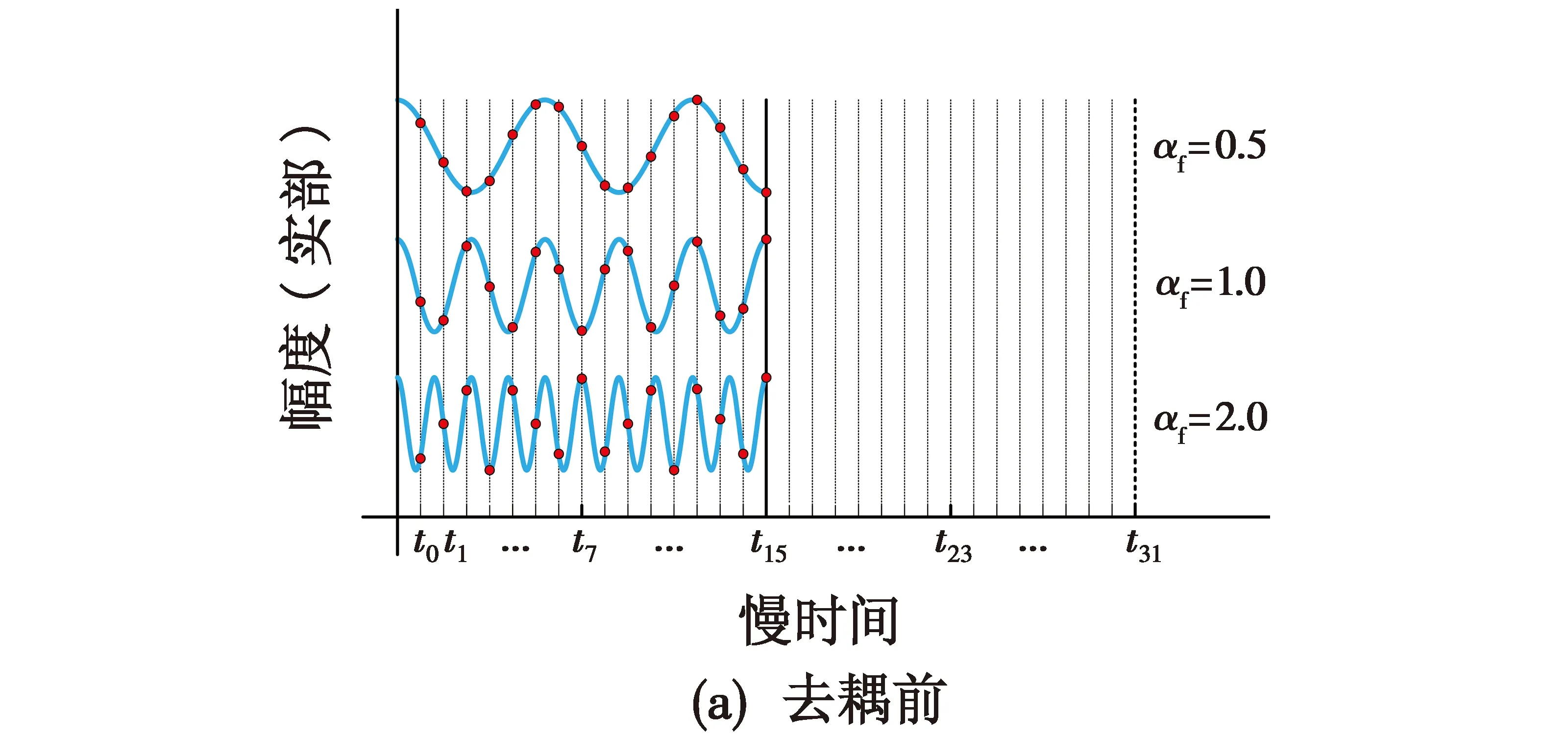
图2 实际的去耦合过程示意图

图3给出了基于TS的Keystone变换实现思路,难点在于TS数值计算。

为确保去耦后信号采样点数相同,当αf>1时,需要对TS后信号时域截取前M个采样点,当αf<1时,需要在TS后信号时域补零,补零个数为

(10)

ceil(0.05M)。

3 基于快速FFT插值的Keystone变换去耦合算法原理

为实现KT去耦合,需要解决TS数值计算问题。由于TS会改变信号时宽,插值不可避免,寻找一种低计算量插值算法,可以解决TS快速计算问题。FFT插值是一种高效的插值算法,但为整数倍插值,KT中的TS要求非整数倍插值,本章将针对该问题给出解决方案。

3.1 FFT插值

FFT插值是一种整数倍插值算法[16-17],整个过程仅使用了1次FFT和1次IFFT。设插值前序列x(n)为实序列,长度为N1,插值后序列y(m)同样为实序列,长度为N2,R为插值倍数,N2=N1R,FFT插值具体步骤如下。

1) 步骤1。计算x(n)的N1点FFT,得到XN1(k)。

2) 步骤2。创建长度为N2的序列YN2(l),当N1为奇数时,令

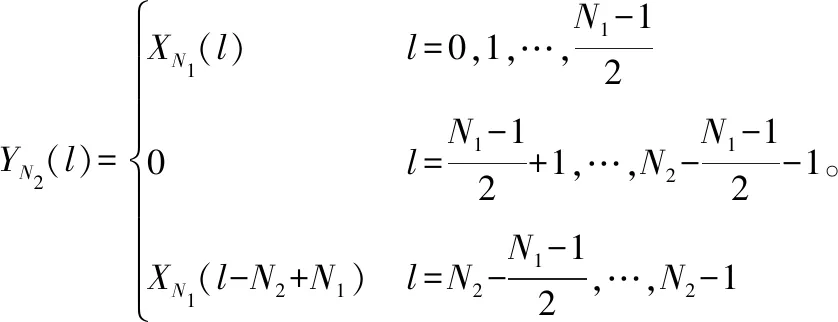
(11)

当N1为偶数时,令

(12)

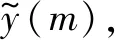
(13)

式中,real[·]表示取实部。步骤2为FFT插值算法核心,为直观显示,设N1分别为8和9,插值倍数为2,图4为频域补零示意图,图中,红色标记为正频率,绿色标记为负频率,黑色标记为截止频率,蓝色标记为补零频点。

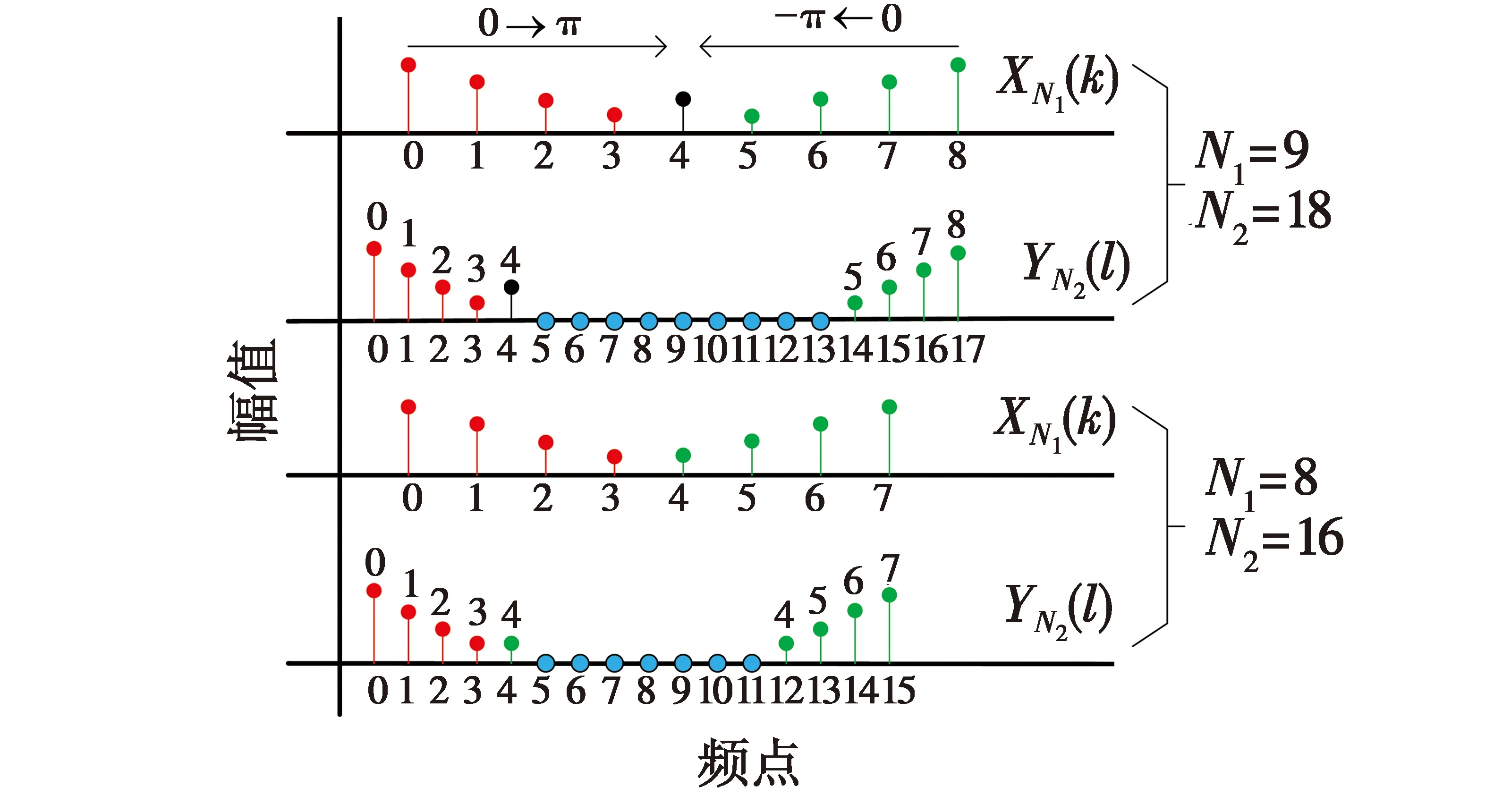
图4 频域补零示意图

由上述步骤可知,FFT插值具体操作为高频补零,等效为低通滤波,与常用辛格插值相似,补零个数为N2-N1(N1为奇数)和N2-N1-1(N1为偶数)。由步骤1～3还可知,为得到插值后的序列,需要进行1次N1点FFT和1次N2点IFFT,总共需要的复乘次数为0.5N1lbN1+0.5N2lbN2,计算复杂度为O(N2lbN2),低于文献[8]方法。另外,FFT插值还有一种计算复杂度更低的子序列实现方法[18],基本思想是将1次N2点的IFFT拆分成R-1次的N1点IFFT,总共需要(R-1)(0.5N1lbN1+2N1)次复乘运算,计算复杂度为O(N2lbN1),在此不做详述。YN2(l)实际上并不是原始信号以Rfs为采样频率计算得到的频谱,因此存在插值误差,可对补零后频谱前后几个点加窗以减少误差[16]。

3.2 利用改进的FFT插值算法实现一维信号时间尺度操作

3.1节介绍了FFT插值基本原理,经典FFT插值设定插值前序列为实序列、插值倍数为整数,而KT耦合项为解析信号、尺度因子为1附近的小数,因此利用FFT插值计算TS需要解决解析信号适用性及非整数倍插值问题。对于第1个问题,易知解析信号DFT为单边谱,而实序列DFT为双边谱,利用式(11)、式(12)进行补零同样可行,仅是当N1为偶数时,将YN2(N2-N1/2)置零即可,因为式(12)中对l=N2-N1/2的赋值是为了满足实值序列频谱的共轭对称性;对于第2个问题,需要知道插值后序列表示式,计算式(11)、式(12)的离散傅里叶逆变换。当N1为奇数时,可得

(14)

令m=N2r/N1,得到

(15)

将式(15)代入式(13)可得插值后的序列表示式为

y(rN2/N1)=y(Rr)=x(r)。

(16)

同理,当N1为偶数时,可得

(17)

同样,令m=N2r/N1,进一步得到

(18)

将式(18)代入式(13)可得插值后的序列表示式为

y(rN2/N1)=y(Rr)≈x(r)。

(19)

综合式(16)、式(19)可知,当插值倍数为整数时,插值后的第Rr值与插值前的第r值近似一致;当插值倍数非整数时,插值后的第N2r/N1值与插值前的第r值近似一致,FFT插值可理解为TS的离散形式,尺度因子α为N1/N2(对应αf=N2/N1),通过改变频域补零个数可实现TS。当αf>1时,频域补零个数取

Nz1(αf)=ceil(αfN1-N1)。

(20)

当0<αf<1时,利用式(20)补零显然是不合理的,因为Nz1(αf)为负整数,可采取“频域补零+时域抽取”的方法实现,补零个数为

Nz2(αf)=ceil(LαfN1-N1)

(21)

式中,L为抽取倍数,L=ceil(1/αf),对于窄带雷达,L=2。为直观显示,图5给出了基于FFT插值的TS实现流程,结合图3可得完整的KT实现过程。

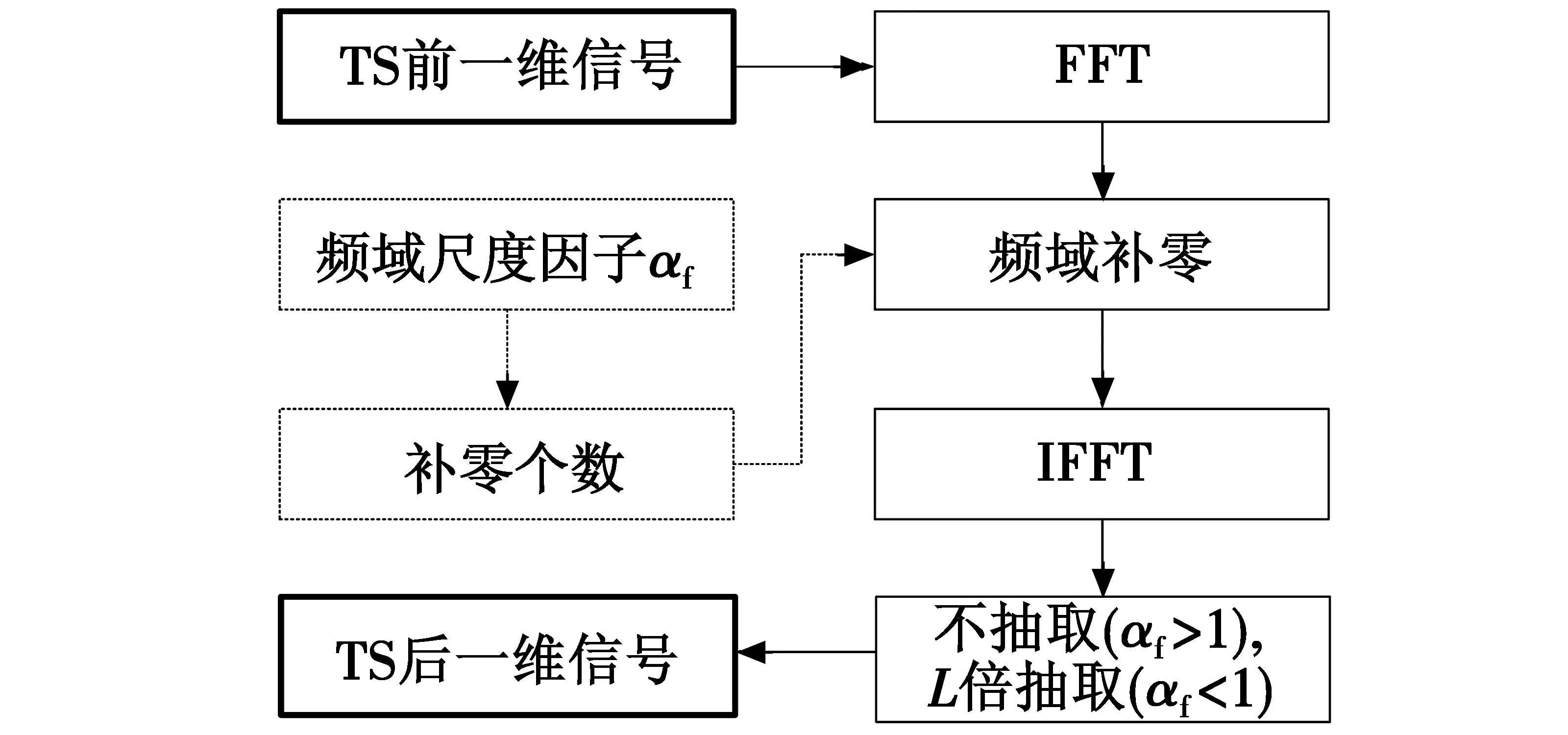
图5 基于FFT插值的TS实现流程

图5涉及频域补零、L倍抽取问题,而图3又涉及时域截取、补零,在此举例说明。设TS前信号即耦合项φ(αf,tm)长度为256,256同样为相参积累个数,频率尺度因子αf为1.05,根据式(20)可得频域补零个数为13,进而得到TS后信号φ(1,tm)长度为269,由于理想KT去耦合过程要求去耦后信号数字采样点数相同,截取TS后信号前256个点;同理,设频率尺度因子αf为0.95,根据式(21)可得抽取倍数L=ceil(1/αf)=2,频域补零个数为231,进而得到TS后信号φ(1,tm)长度为487,再进行2倍抽取(长度为243),由于理想KT去耦合过程要求去耦后信号数字采样点数相同,对抽取后的信号补13个零。

3.3 计算复杂度分析

现有KT实现方法主要包括辛格插值法[8]、Chirp滤波法[9]和“CZT+IFFT”方法[10],其中,“CZT+IFFT”方法计算量最低。本节对比“CZT+IFFT”方法,对所提方法计算复杂度进行分析。设回波信号经下变频、脉冲压缩、快时间FFT,得到M×P的二维矩阵,M为积累脉冲数,P为快时间频率点数(奇数)。“CZT+IFFT”方法去耦合过程包含CZT和IFFT两步,共需(P-1)[M1+2M+1.5M1lbM1+0.5MlbM]次复乘[9],M1为大于2M-1的正整数,计算复杂度为O(PM1lbM1)。所提方法包含3步,分别为FFT、频域补零和IFFT,对于1个快时间频率单元回波,计算FFT均需要进行0.5MlbM次复数乘法,而计算不同快时间频率单元回波IFFT所需的复乘次数,与补零后的频谱长度有关。由式(20),(21)可知,当αf>1时,补零后的频谱长度为Nz1(αf)+N1,当0<αf<1时,补零后的频谱长度为Nz2(αf)+N1。由于αf=(f+f0)/f0是关于快时间频率f的连续信号,将其表示成离散形式为

(22)

式中,p=-(P-1)/2,…,0,…,(P-1)/2。所提算法总共需要的复乘次数Nnum为

(23)

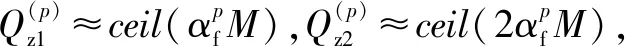
Nnum<0.5(P-1)MlbM+(P-1)Mlb (2M)。

(24)

所提方法计算复杂度为O[PMlb (2M)],低于“CZT+IFFT”方法。设P分别为2001,4001,αf取值0.95～1.05,相参积累个数为16～1000,图6给出了复乘次数随积累脉冲数变化曲线,相同快时间频率点数下所提方法需要的复乘次数更少。

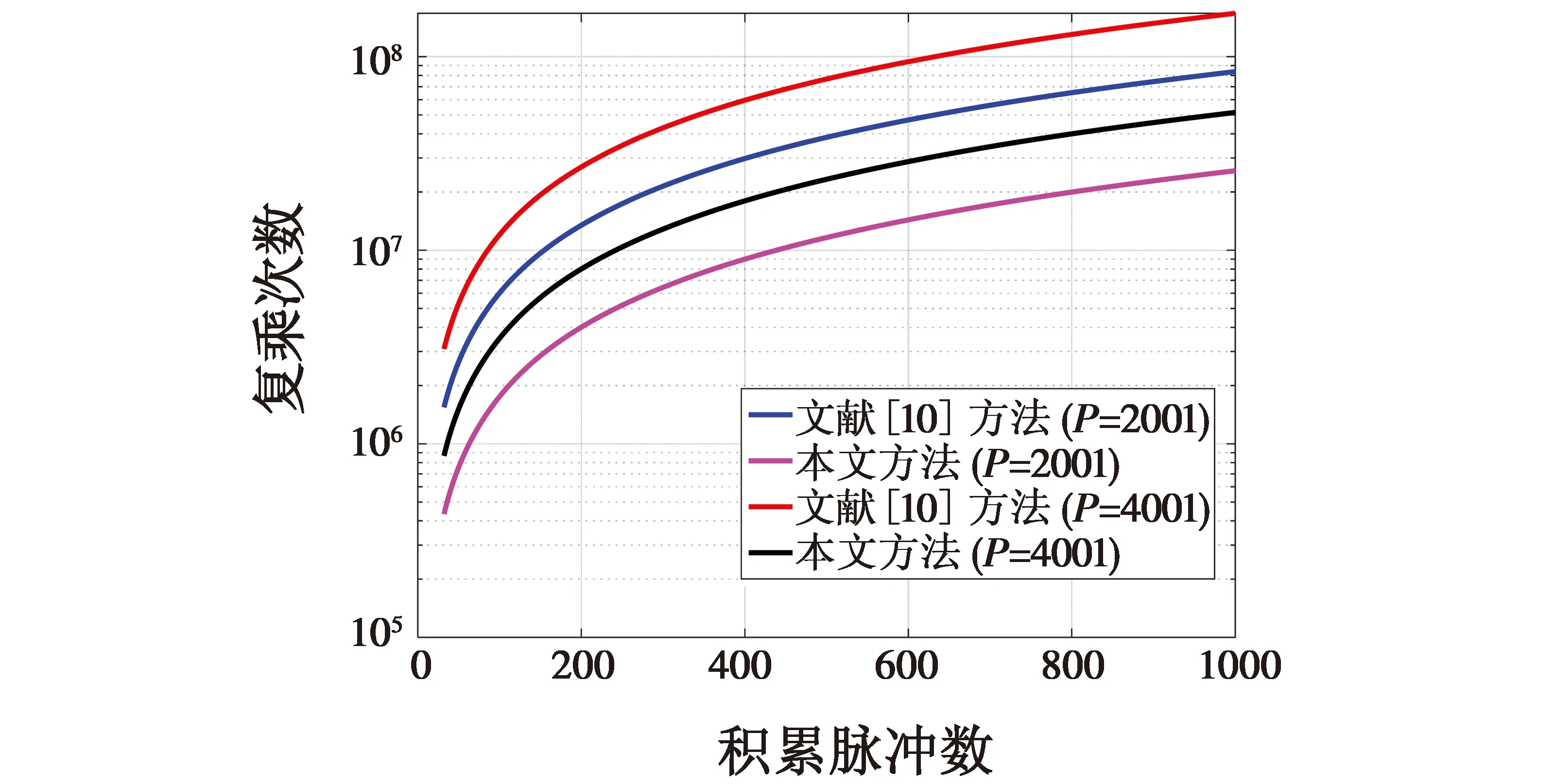
图6 复乘次数随积累脉冲数变化曲线

直观上看,“CZT+IFFT”方法为实现1个快时间频率单元回波去耦合需要进行2次Chirp乘积、1次Chirp卷积和1次IFFT,所提方法仅需1次FFT和1次IFFT(不考虑频域补零、时域截取、时域补零产生的运算量),计算量明显更低。

4 仿真结果与分析

4.1 参数设置

雷达载频为0.5 GHz,脉冲重复频率为10 kHz,相参积累个数为256,发射信号为LFM脉冲信号,脉宽为15 μs,带宽为20 MHz,采样频率为40 MHz,雷达探测范围内1个高速点目标向站匀速飞行,初始距离为8 km,不模糊速度为450 m/s,模糊数为41。

4.2 可行性分析

对所提基于FFT插值的KT可行性进行验证,为显示细节,仿真回波中不考虑噪声,下一节将进行算法抗噪效能分析。首先,对回波快时间脉冲压缩结果如图7所示,目标存在明显距离走动。

其次,对脉压后回波快时间做FFT,沿慢时间进行模糊数补偿(真实模糊数),再沿快时间频率做IFFT,观察“模糊数补偿”环节对目标距离走动校正的影响,结果如图8所示,目标慢时间上仍未完全对齐。

图8 模糊数补偿后回波

然后,对图8回波快时间做FFT,沿慢时间进行TS,再沿快时间频率做IFFT,完成目标距离走动校正,结果如图9所示,目标在慢时间上完全对齐。上述涉及模糊数估计问题,可以采取循环搜索最大峰值的方式得到。

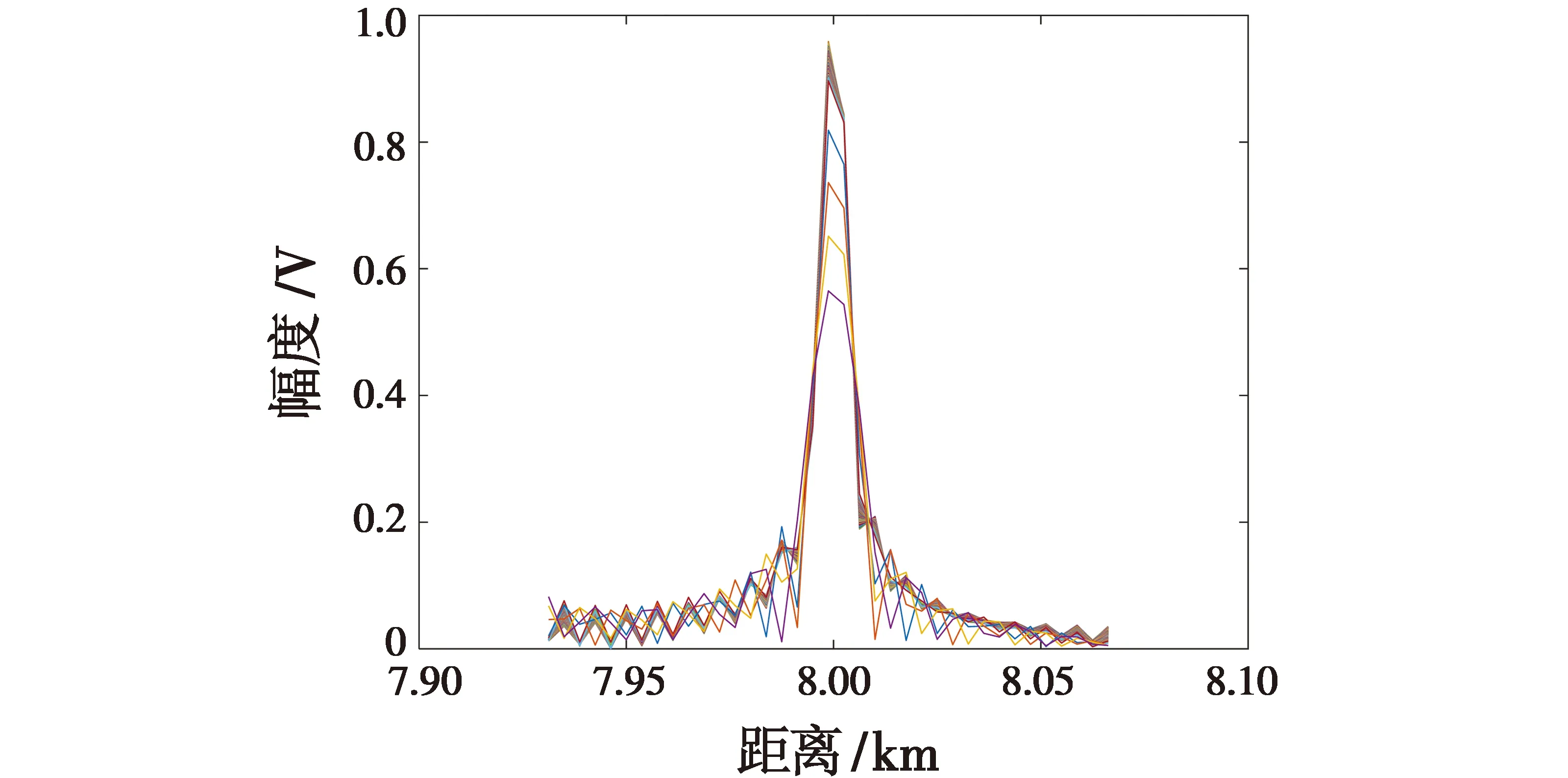
图9 时间尺度后回波

最后,对图7、图9分别沿慢时间做FFT完成相参积累结果,如图10所示,校正前无法检测目标,校正后目标得到充分聚焦,峰值搜索可得目标初始距离为8 km,不模糊速度为453 m/s,与仿真参数基本一致。由于图10已对回波进行了增益归一化,目标理论幅值应接近1 V,而实际得到的目标幅值为0.82 V,说明KT对目标存在一定的处理损失(现有方法均如此,且不可避免),下面将针对该问题,对不同的KT实现方法处理损失及能量聚焦性进行评估。

图10 回波相参积累结果

4.3 抗噪效能分析

对基于FFT插值的KT实现方法抗噪效能进行分析,使用的评估指标为输出信噪比(SNR-out)和瑞利熵(RE)[19],前者用于评估不同KT实现方法对目标的处理损失程度,后者用于评估相参积累后回波能量聚焦程度。相同输入信噪比(SNR-in)条件下,SNR-out越大,熵值越小,说明KT对目标的处理损失越小,目标聚焦性越好。另外,仿真计算SNR-out时,已对回波脉压增益、相参积累增益进行了归一化,且下文中的参数设置能够确保目标被有效检测。设相参积累个数为128,SNR-in取值-15～5 dB,间隔2 dB,运行蒙特卡罗仿真500次,KT抗噪效能曲线如图11所示。设目标不模糊径向速度为900 m/s,KT抗噪效能曲线如图12所示,进一步设雷达载频为1 GHz,KT抗噪效能曲线如图13所示。可以看出:图11(a),12(a)和13(a)中的黑色线条(对应所提方法)多位于其他线条的上方,说明所提方法处理后的目标峰值高于文献[8-10]方法;图11(b),12(b)和13(b)中的黑色线条多位于其他线条的下方,说明所提方法处理后的回波能量聚焦性更强。

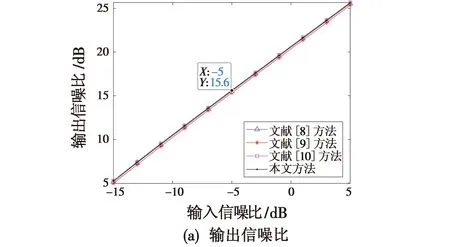
图11 KT抗噪效能曲线(回波脉冲数为128)

图12 KT抗噪效能曲线(目标不模糊径向速度为900 m/s)

5 结束语

针对现有Keystone变换(KT)实现方法计算量和抗噪效能不够理想的问题,提出基于FFT插值的KT实现方法。仿真结果表明,所提方法能够有效校正目标距离走动,抗噪效能优于现有方法,且计算复杂度更低。另外,所提算法使用了FFT,IFFT,频域补零及时域抽取等基础操作,存在工程实现可能。本文利用FFT插值实现时间尺度操作,解决了KT去耦合问题,考虑到吕分布、宽带模糊函数及合成孔径雷达成像等同样面临时间尺度数值计算问题,所提方法均可应用。