基于传感器网络的时延补偿分布式状态估计
2023-10-25何文韬薛鹏翔邢顺翔王威振
何文韬, 陈 欣, 薛鹏翔, 邢顺翔, 王威振
(1.南京航空航天大学自动化学院,南京 210000; 2.中国人民解放军95791部队,甘肃 酒泉 735000)
0 引言
传感器网络(Sensor Network,SN)是指由部署在待监测区域的若干个传感器节点形成的自组织网络系统,具有感知、通信功能[1]。基于SN的分布式状态估计方法具有较好的鲁棒性和灵活性,引起了越来越多的研究关注[2-7]。在大量关于分布式状态估计的研究中,两种广泛使用的方法是共识策略和扩散策略。共识卡尔曼滤波算法最早在文献[2]中提出,为了使局部估计达成共识,局部滤波完成后在相邻节点之间交换测量信息来协调局部估计;文献[3]研究了最优共识卡尔曼滤波算法问题,并分析推导出了最优增益;文献[4]为加权有向图设计了一种改进的最优基于共识的滤波算法。扩散卡尔曼滤波算法是在文献[5]中提出的,该算法利用文献[2]中的局部卡尔曼滤波器计算来自邻居的测量信息的先前估计,并且与迭代共识方法相反,应用了邻居的先前估计的凸组合。在此结果的激励下,设计了一类基于扩散策略的分布式自适应滤波算法[6]。与共识策略相比,扩散策略可以与输入测量进行实时融合,并且具有更快的收敛速度和更小的均方误差[7]。
以上提及的关于SN分布式状态估计的研究,没有考虑到网络的带宽限制问题。然而,组成SN的探测节点的能源一般由电池供应,电池功率的受限带来通信带宽受限的问题。因此,基于量化信息的滤波器设计是一个重要的问题[8]。量化将测量信号转换为在有限集上取值的分段常数,这一过程降低了带宽的要求,但引入了误差。迄今为止,人们已经为解决量化效应影响的控制/估计问题付出了巨大的努力。文献[9]将量化视为原始信号信息的一部分,而不是近似,这为后续的量化研究奠定了基础;文献[10]研究了一类具有对数量化和缺失测量的非线性系统基于事件的状态和故障估计问题;文献[11]提出了一种基于量化测量新息而不是原始信号的分步式无迹卡尔曼滤波估计器;在此基础上,文献[12]提出了一种具有量化信息交换的扩散卡尔曼滤波算法。
此外,在网络化系统中,由于数据是通过网络传输的,因此不可避免地存在网络诱导时延现象,导致网络化系统的估计精度下降[13-14]。为了处理传感器延迟,文献[15-16]利用测量重组方法,先获得一组无延迟的测量,再进行状态估计。将传感器延迟建模为服从伯努利分布的随机变量是近年来广泛使用的一种方法[17-20]。当伯努利分布随机变量为1时,系统中存在传感器延迟;否则,接收到的测量值正常。然而,上述方法只能应对单步或两步传感器延迟下的状态估计。对于多步传感器延迟,文献[21]采用缓存器存储量测时延数据,设计了具有时延补偿的UKF算法。
本文提出一种基于量化信息的时延补偿分布式无迹卡尔曼滤波(Quantization-based Distributed Unscented Kalman Filter with Time Delay Compensation,QDUKF-TDC)算法,用于目标的分布式状态估计。本文的贡献可以归纳如下。
其一,引入一种自适应量化机制,用于节省通信带宽。与传统的概率量化机制相比,自适应量化机制能够自适应地改变量化区间的长度,获得更高的估计精度。
其二,给出了基于SN的QDUKF-TDC算法设计,可用于获得具有随机传输时延的网络化系统的状态估计。
1 问题描述
考虑一个包含N个传感器和远程估计器的离散非线性系统,传感器监测目标的系统模型和测量输出为
(1)

1.1 自适应概率量化
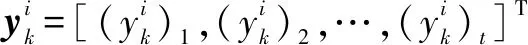
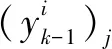
(2)
式中,l为量化位数。


(3)

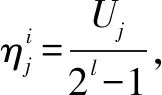

(4)


(5)

(6)
1.2 随机传输时延

(7)
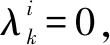
定义函数
(8)
式中,j≥0,且j为整数。

2 分布式时延补偿无迹卡尔曼滤波器
本章将推导基于量化信息的分布式时延补偿无迹卡尔曼滤波算法。
2.1 改进的无迹卡尔曼滤波器(UKF)
考虑到UKF避免了线性化的过程而具有更高的估计精度,设计了改进的UKF局部估计器。对于第i个估计器,状态估计更新方程定义为
(9)
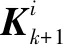

将式(4)的量化误差定义代入式(1)的系统模型得到
(10)


(11)

证明。


(12)
证毕。
接下来,进行局部估计器的设计。
定理2对于带有自适应概率量化机制和随机传输时延的非线性系统(式(1)),所设计的第i个局部估计器的滤波器增益和协方差更新方程为
(13)
(14)
(15)

(16)
证明。

(17)
估计误差协方差为
(18)
令
(19)

根据定理1,可得
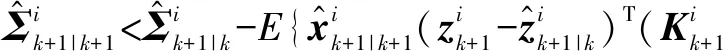
(20)
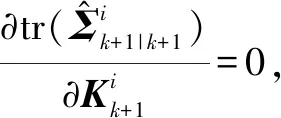
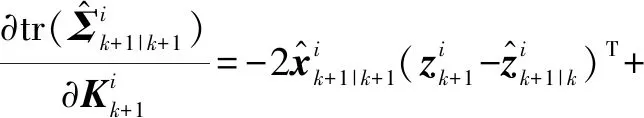
(21)


(22)
协方差更新的规则如下
(23)

(24)
证毕。
完整的改进无迹卡尔曼滤波算法实现过程总结如下。
算法1 基于量化信息的分布式无迹卡尔曼滤波(Quantization-based Distributed Unscented Kalman Filter,QDUKF)算法。算法步骤如下。
1) 计算Sigma点。
(25)
式中:a为比例参数;n为系统阶数。
2) 计算k+1时刻的预测状态及其协方差
(26)
(27)

(28)
(29)
(30)

(31)
(32)

3) 按照式(13)计算增益矩阵。
4) 按照式(9)进行状态更新,按照式(14)进行协方差更新。
5) 在下一个采样时刻重复1)~5)。
时延补偿思想:在每一时刻,局部估计器利用缓存器里暂存的数据循环更新估计值,达到降低时延对估计精度影响的目的。在k时刻局部估计器时延补偿的流程如下:

注2 时延补偿算法利用了距离当前时刻D步以内的过去时刻收到的数据包进行循环更新,而QDUKF算法只利用当前时刻收到的数据包进行更新,因此,时延补偿算法降低了时延对估计精度的影响。
2.2 基于快速协方差交叉的融合方案
得到局部传感器状态和误差方差后,根据快速协方差交叉方法[6]计算融合后的状态和相应的误差方差为
(33)

至此,完整的算法流程如下。
算法2 基于量化信息的时延补偿分布式无迹卡尔曼滤波(QDUKF-TDC)算法。算法步骤如下。
1) 按照算法1的1)~3)进行。
2) 进行时延补偿

3) 得到局部传感器状态和误差方差后,按照式(33)计算融合后的状态和相应的误差方差。
4) 在下一个采样时刻重复1)~4)。
3 融合估计误差有界性分析
对设计的时延补偿分布式无迹卡尔曼滤波器的估计误差进行分析,以证明算法的收敛性。首先,为了后续的推导,介绍一个引理。
引理1[22]对于A,B∈Rn×n,如果A,B是对称正定矩阵,则
(A+B)-1>A-1-A-1BA-1。
定义预测误差和残差为
(34)
(35)
误差表达式可以简化为
(36)
(37)

(38)
(39)
(40)
根据式(14),(38)~(40),可得
(41)

(42)
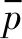
(43)
证明。
根据式(38)和(41),可得

(44)
根据引理1的条件,可得
(45)
利用式(42),可得
(46)
(47)


得

(48)

证毕。
4 仿真分析
用一个仿真算例来验证所提出的算法的有效性和实用性。
利用4架配备机载雷达的无人机对地面上的非合作机动目标进行感知和跟踪,每架无人机将测量信息经过自适应概率量化后传回对应的远程局部估计器。
使用以下转弯模型来预测所考虑的非合作机动目标的运动模型
(49)

传感器的测量方程为
(50)

注3 对于非线性函数,拓展卡尔曼滤波由于忽略了高阶项,会降低滤波精度甚至发散,UKF没有引入线性化误差,估计精度更高。

采用均方根误差(RMSE)作为衡量算法性能的指标,其定义为
式中,L为仿真步数,本次仿真设置为100。
为了比较本文自适应量化策略和文献[8]中量化策略的估计误差,以传感器1为例,将所提出的QDUKF算法与传统量化策略下的UKF(TQDUKF)算法进行比较。仿真结果如图1所示,QDUKF算法的跟踪误差小于TQDUKF算法。
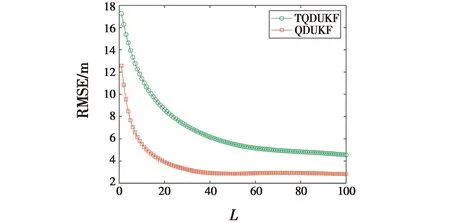
图1 传感器1不同量化策略估计误差
以传感器1为例,随机传输时延如图2所示,基于共识的QDUKF和QDUKF-TDC算法的误差比较如图3所示。由于引入了时延补偿机制,QDUKF-TDC算法比QDUKF算法具有更小的共识误差。

图2 随机传输时延示意图

图3 传感器1有无时延补偿估计误差
图4和图5所示为4个传感器节点的RMSE与QDUKF-TDC算法RMSE的比较,以及融合估计的轨迹。
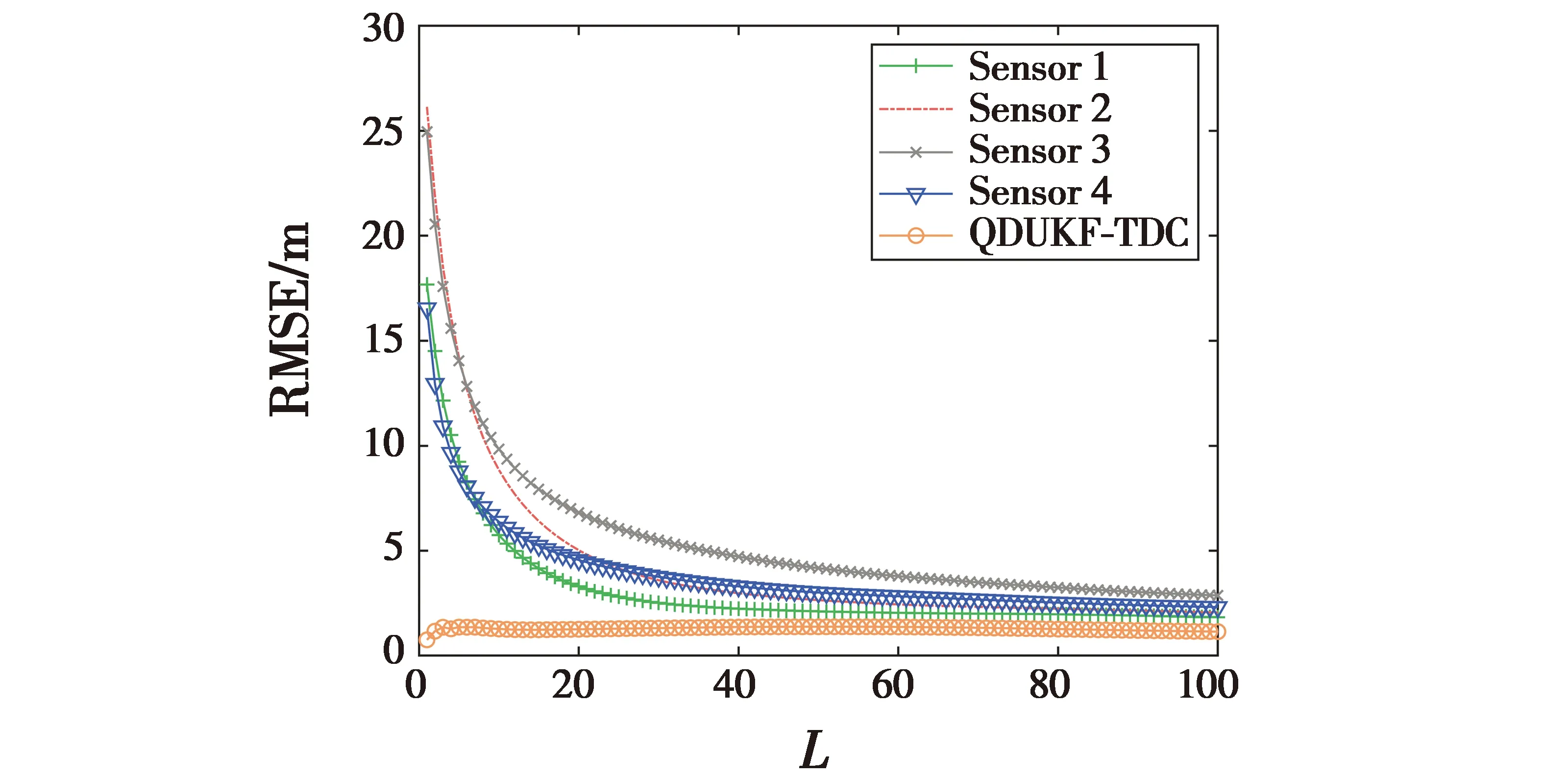
图4 融合估计和局部估计的估计误差

图5 融合估计的轨迹
由图4和图5可以看出,QDUKF-TDC算法的RMSE小于所有单个传感器节点,表明QDUKF-TDC算法具有最好的目标跟踪性能。
5 结论
本文提出了一种时延补偿分布式状态估计算法,用于具有随机传输时延的网络化系统。为了减少通信带宽的占用,引入了自适应量化策略。由于随机传输时延的存在,使用缓存器暂存量测数据。然后,考虑量化误差的影响,利用缓存器中的数据,设计了时延补偿分布式无迹卡尔曼滤波器(QDUKF-TDC),并利用快速协方差交叉技术完成各个节点的信息融合。最后,通过数值模拟验证了QDUKF-TDC算法的有效性。值得注意的是,在实际应用中还存在很多问题,如测量衰减、噪声相关系统的分布式估计算法等,这些都是未来研究中需要考虑的。
