自适应随机权重容积卡尔曼滤波交互多模型目标跟踪
2023-10-25李春菊
宋 伟, 李春菊
(1.民航西北地区空中交通管理局宁夏分局,银川 750000; 2.宁夏工商职业技术学院,银川 750000)
0 引言
在状态估计和信息融合领域,机动目标跟踪问题依然是一个热点问题,广泛应用于导航、航空交通以及军事等相关领域。在航空运输领域,为了完成空中机动目标的跟踪,必须要考虑目标运动模型匹配精度和滤波器性能两个重要因素。
目标跟踪模型就是研究跟踪系统的状态模型是否匹配目标实时运动模型。目标的运动过程非常复杂,用单一模型模拟整个运动过程是非常困难的。因此,交互多模型(IMM)算法被提出,以解决此类问题。IMM算法同时并行处理多个模型,模型之间的转换通过概率转移矩阵实现[1]。
机动目标跟踪问题中,运动模型一般是非线性的,因此,选择合适的滤波器显得非常重要。文献[2]利用扩展卡尔曼滤波解决非线性系统问题,其基本思想是先通过泰勒展开式把非线性系统问题近似为线性系统问题,再进行卡尔曼滤波,在简单的非线性系统中,该算法具有很好的跟踪精度和很少的计算量,但在复杂的非线性系统中,该算法却无法很好地解决实际问题;文献[3]中,容积卡尔曼滤波算法(CKF)被用作IMM算法的子模型,很好地完成了跟踪任务;文献[4]利用随机权重因子代替初始因子来减少系统噪声的影响,随机权重容积卡尔曼滤波算法被提出。
针对上述问题,本文提出了一种自适应随机权重容积卡尔曼滤波交互多模型跟踪算法,该算法改善了滤波精度,同时提升了算法稳定性能。
1 容积卡尔曼滤波算法简介
一般非线性系统的数学模型表示为
(1)
式中:xk和zk分别为系统状态向量和测量向量;Wk和Vk分别为系统过程噪声和测量噪声,两者是相互独立的零均值白噪声,且对应的协方差分别为Qk和Rk;f(·)和h(·)分别为非线性系统状态转移函数和测量函数。系统初始状态x0~N(0,P0),与Wk-1和Vk互不相关,P0为初始协方差矩阵[5]。

(2)
式中,Sk-1|k-1为协方差矩阵的平方根系数。因此,容积点算式为
(3)

(4)
因此,在容积点i从k-1时刻到k时刻的状态预测和方差分别为
(5)
(6)
测量更新如下。
分解预测误差协方差矩阵Pk|k-1为
(7)
计算容积点i从k-1时刻到k时刻的系统状态向量为
(8)
容积点i从k-1时刻到k时刻的测量向量为
(9)
容积点i从k-1时刻到k时刻的测量预测、方差和协方差分别为
(10)
(11)

(12)
滤波器在k时刻的增益为
(13)
计算k时刻的状态估计为
(14)
均方差矩阵为
(15)
如果非线性系统包含较大的误差,那么系统状态模型和测量模型为
(16)
式中:Δxk为预测模型误差;Δzk为测量模型误差。
那么状态预测为
(17)
测量预测为
(18)
通过以上可以看出,如果非线性系统引入了误差,那么状态预测和测量预测均存在偏差,而且滤波器增益也存在偏差,导致整个系统状态估计不准确。因此,若存在系统模型误差,那么CKF估计也会存在误差[4]。以上也可以证明测量预测和状态预测、协方差都通过初始权重计算,所有容积点的预测误差不能精确表达实际系统误差的统计特性,因此本文引入随机权重。
2 自适应随机权重容积卡尔曼滤波
2.1 随机权重容积卡尔曼滤波
假设x1,x2,…,xn是一组具有相同概率分布的随机变量,分布函数为F(x)[7]。那么,分布函数可以表示为
(19)
式中,I(xi≤x)为指示函数。Fn(x)的随机权重定义为
(20)
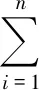
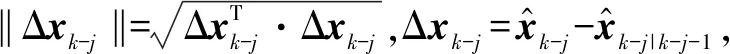
(21)
(22)


(23)
(24)

(25)
(26)
λi随着前后时刻误差的变化而变化,实时反映出误差对以上变量的影响,因此,基于随机权重的容积卡尔曼滤波的精度更高。
2.2 自适应跟踪算法
基于自适应思想可以更新系统噪声协方差矩阵Qk和测量噪声协方差矩阵Rk[9]。通过引入时变因子可以改善算法的稳定性[10]。自适应滤波算法具体算式为
(27)
(28)

(29)
(30)
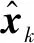
在实际应用中,当Qk-1和Rk均未知时,同时更新Qk-1和Rk易导致算法崩溃,因此本文把Rk设置为常量。因为在式(29)中的负号会产生负矩阵结果,为了使Qk-1半正定,设均值方差Pk和Pk-1为零。改进的自适应滤波算法为
(31)
3 交互多模型自适应随机权重容积卡尔曼滤波算法
交互多模型自适应随机权重容积卡尔曼滤波(IMM-ARWCKF)算法主要由交互作用器、多个滤波器、一个状态估计融合器和模型概率估计器组成[11]。IMM-ARWCKF算法计算步骤如图1所示。

图1 IMM-ARWCKF算法计算步骤
IMM-ARWCKF算法可以总结为以下几个步骤[12]。
1) 步骤1:交互输入。
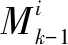
(32)
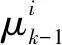
(33)
(34)

2) 步骤2:更新模型概率。
计算第j种模型的可能性
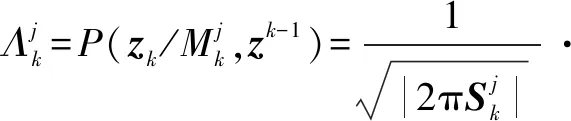
(35)

(36)

3) 步骤3:状态交互融合。基于模型概率融合各模型滤波预测,得到k时刻的最终结果为
(37)
(38)
4 改进的马尔可夫概率矩阵
本文利用后验概率信息调整马尔可夫转移概率矩阵[14]。由于指数函数的单调性和概率变化的非负性,定义以下因子
(39)

(40)


(41)
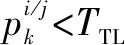
(42)
其中,TTH和TTL分别代表转移矩阵的上限和下限。出于时变因子的原因,转移概率矩阵的元素也是变化的。变化的随机性会导致两个问题:在特定时间,不同模型的概率不能是1;主对角线元素的调整会导致主对角线优先权的丧失[16]。本文设定了主对角线元素的上下限值来解决此问题。实验结果表明,上限TTH=0.97,下限TTL=0.92时会得到比较好的结果。
5 实验和结果
通常使用均方误差来评估航迹跟踪结果,即
(43)
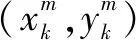
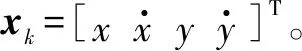
xk=FCVxk-1+Γwk
(44)


xk=FCTxk-1+Γwk
(45)
(46)
其中:ω为圆周运动的角速率,ω>0表示向左转弯,ω<0表示向右转弯;wk是具有零均值的二维高斯白噪声。目标的测量方程是线性的,表示为
zk=Hxk+Vk
(47)
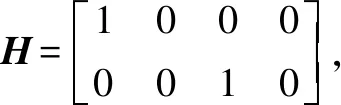
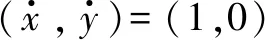

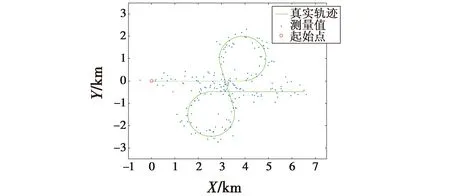
图2 运动目标的真实航迹
图3、图4是IMM-ARWCKF与其他3种算法比较的结果。IMM-ARWCKF算法充分利用了条件概率后验信息,当目标状态发生变化时可以快速匹配真实目标运动航迹,因此IMM-ARWCKF算法的跟踪效果最优。

图3 滤波器对目标的估计
各滤波器误差分析如表1所示。结果表明本文IMM-ARWCKF算法有更小的均方误差。与IMM-CKF算法进行比较,IMM-ARWCKF在两个方面进行了优化:一方面,使用随机权重因子使得CKF算法中的估计值更加趋近真实值;另一方面,利用残差序列更新噪声协方差矩阵和状态估计协方差矩阵使得算法更加稳定。

表1 各滤波器误差分析
6 结论
针对非线性系统机动目标跟踪问题,本文提出了一种IMM-ARWCKF算法。该算法主要优点有:1) 使用自适应随机权重容积卡尔曼滤波作为IMM滤波器的子滤波器作用于不同的运动模型上,引入随机权重因子来替换初始因子,从而提高了算法精度;2) 为了算法稳定性,添加自适应强跟踪滤波器来更新预测协方差矩阵和噪声协方差矩阵;3) 通过引入时变因子调整转移概率矩阵,改进IMM算法概率协方差精度,该算法结合IMM算法和ARWCKF算法有效解决了非线性系统机动目标跟踪问题。
