位移采样下二阶多智能体系统的脉冲一致性
2023-10-25廖毅豪罗世贤
蒋 燕, 廖毅豪, 罗世贤, 林 波
(广西大学电气工程学院,南宁 530000)
0 引言
二阶多智能体系统能够刻画物理系统的动力学特征,被广泛应用于智能电网分布式控制[1]、移动机器人协同控制[2]和编队控制[3]等领域。二阶一致性是指二阶智能体通过与邻居通信使其速度和位移最终达成一致。如何设计控制算法实现二阶一致是研究二阶多智能体系统的主要任务之一。近年来,二阶多智能体的一致性问题得到了深入研究,并在模型上进行了推广,例如时滞系统、随机系统、切换拓扑及非线性系统等。
在网络通信背景下,由于通信带宽与通信成本限制,许多学者利用采样控制和脉冲控制策略对二阶多智能体系统的一致性问题进行研究。例如,文献[4-5]研究了二阶多智能体系统采样一致性控制问题;文献[6-7]在文献[4]基础上考虑了仅有采样位移信息的一维线性多智能体系统的采样控制问题。不同于连续反馈的采样控制,脉冲控制[8]仅在采样时刻施加控制,属于典型的点控制,其因消耗能量少、实现相对简单等特点,被应用于二阶多智能体系统的一致性算法设计。例如,文献[9-11]利用根轨迹法,建立了仅含位移测量信息的一维二阶多智能体系统的脉冲一致性判据;文献[12]在文献[10]基础上分别建立了固定拓扑和随机拓扑下一致性有界跟踪的充要条件;随后,文献[13]将文献[10]的结果进一步推广到了耦合谐振子的符号网络。尽管基于采样位移信息的采样/脉冲控制算法取得了丰硕成果,但是这些结果具有一定的局限性:1)所提出的一致性控制算法只适用于单输入单输出的一维动力学模型;2)以离散化或根轨迹法作为主要的收敛性分析方法,难以推广到多输入多输出的高维多智能体系统,且不适用于含有参数不确定性的系统。此外,注意到已有关于二阶多智能体系统的鲁棒一致性问题的研究成果。例如,文献[14]利用平方和技术解决含外部扰动的二阶多智能体系统鲁棒二阶一致问题;文献[15]针对含有位移和速度的一般二阶多智能体系统,研究未知输入时滞对鲁棒一致性算法的影响机理。但是,这些结果的一致性算法采用位移与速度信息作为反馈,并没有考虑系统速度信息不可测量的情形。因此,针对一般的线性二阶多智能体系统,应如何设计仅含采样位移信息的分布式脉冲控制算法,并发展新的一致性分析方法,实现鲁棒二阶一致性?
本文针对一般的线性二阶多智能体系统,设计仅含采样位移信息的分布式脉冲一致性算法。主要工作如下:1)在文献[6,14-15]的基础上,考虑系统速度信息不可测量的情形,利用当前和上一次的采样位移信息,结合差分法逼近多智能体的速度,构建与通信拓扑相关的脉冲控制协议;2)相较于文献[9-13]中的根轨迹收敛性分析方法,本文借鉴文献[16]的分析方法,将闭环系统建模为线性脉冲系统,利用谱分析和拟周期Lyapunov函数方法,给出具有多输入多输出高维二阶多智能体系统能够实现二阶一致性的判据,揭示采样周期、脉冲控制器增益及拉普拉斯矩阵的特征值对实现二阶一致性的影响机理;3)研究采样周期和系统参数的鲁棒性对分布式脉冲一致性算法的影响,并以低维数(不依赖多智能体的数量)的线性矩阵不等式,给出能够实现鲁棒一致性的判别准则。
1 系统模型
1.1 预备知识

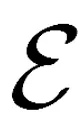
1.2 模型描述
考虑N个智能体组成的二阶多智能体系统
(1)
式中:xi(t)∈Rn和vi(t)∈Rn分别表示第i个智能体的位移状态和速度状态;ui(t)∈Rm,为第i个智能体的控制输入;A0,A1∈Rn×n,B0∈Rn×m,均为常数矩阵。
注1:与现有的一维(n=1)二阶多智能体系统[6-11,13-15]相比,本文考虑位移和速度信息对系统动力学产生影响的一般高维(n≥1)线性二阶多智能体系统,模型具有一般性。
假设每个智能体在离散时刻只有位移信息测量输出,即
yik=xi(tk)k∈N
(2)
式中:yik为第i个智能体在tk时刻的测量输出;tk为采样时刻,并且采样时间序列{tk}满足t0=0和tk+1-tk=h>0,k∈N。
本文主要目标如下:
1) 利用周期位移测量信息,设计分布式脉冲控制协议实现多智能体系统式(1)二阶一致;
2) 对系统参数的鲁棒性进行分析,并给出实现二阶多智能体系统鲁棒二阶一致的判据。

假设1 无向图G有一棵生成树。
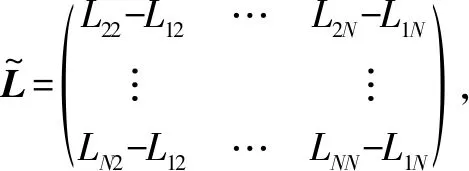
引理2[8]设A,P,D,F,N为维数合适的矩阵,且满足FTF≤I,则对任意矩阵P>0,常数ε>0,下列矩阵不等式成立:
1)DFN+NTFTDT≤ε-1NTN+εDTD;
2) (A+DFN)TP-1(A+DFN)≤εNTN+AT(P-ε-1DDT)-1A。
2 分布式脉冲一致性分析与算法设计
2.1 分布式脉冲一致性算法设计
考虑多智能体的测量输出中仅包含了采样位移信息而不包含速度信息,利用当前时刻的测量输出与过去时刻的测量输出的差分来逼近速度信息。因此,对于系统式(1)中的第i个智能体,利用当前和过去的采样位移信息,设计分布式脉冲一致性协议为
(3)
式中:K1,K2∈Rm×n,为反馈增益;δ(·)为狄拉克函数。

(4)
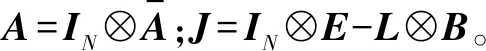
2.2 分布式脉冲一致性分析
实现系统式(1)二阶一致性的判据如下。
定理1如果二阶多智能体系统式(1)满足假设1,且以下条件之一成立,则二阶多智能体系统式(1)在控制协议式(3)的作用下实现二阶一致。
(5)
或
(6)


(7)
(8)
证明。
(9)
因此,系统式(1)实现二阶一致,当且仅当误差系统式(9)渐近稳定。在tk时刻离散化系统式(9),得到离散时间线性时不变系统
(10)
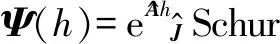

(11)
由式(5)可知,系统式(10)的状态转移矩阵的谱半径小于1,从而多智能体系统式(1)能够实现二阶一致。此外,对式(5)展开,即可得到式(6)。
2) 针对系统式(4),选择拟周期的Lyapunov函数:V2(t)=ηT(t)(L⊗P(t))η(t),∀t∈Δkl[tk+lhk,tk+(l+1)hk),其中,对于任意t∈Δkl,对该Lyapunov函数求导,结合式(7)有
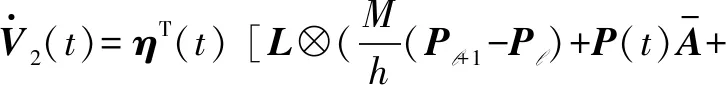
(12)
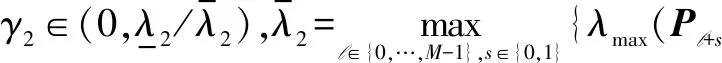
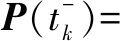
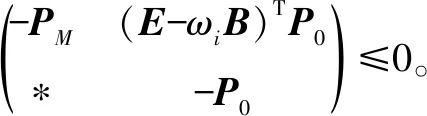
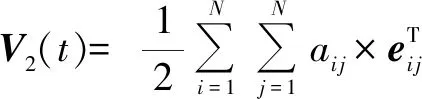
下面针对一维的二阶多智能体系统,给出实现二阶一致性的充要条件。
推论1 若系统式(1)的维数n=1,且A0=A1=0,B0=1,那么系统式(1)可以写成
(13)
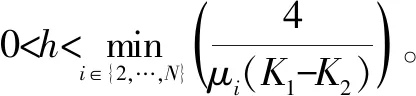
证明。根据定理1的1),仅当系统式(9)的状态转移矩阵的ρ(Ψ(h))<1时,系统式(9)可以实现二阶一致,计算系统式(9)状态转移矩阵Ψ(h)的特征值,有:

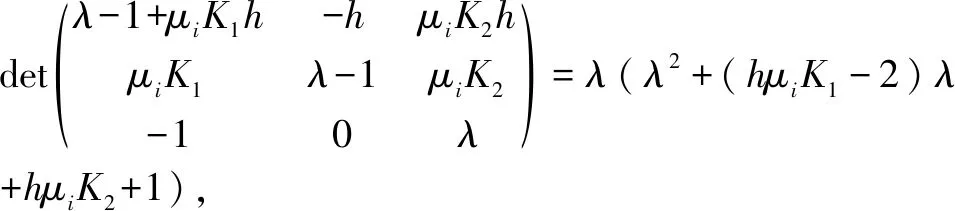
为保证系统式(9)的状态转移矩阵的ρ(Ψ(h))<1,则λ2和λ3的模需小于1。令Δ=(hμiK1)2-4hμi×(K1+K2),下面讨论各种情形。


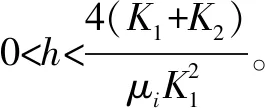

3 鲁棒性分析
3.1 关于采样周期的鲁棒性
在实际的系统中,采样周期可能受扰动影响,如时钟误差漂移、不稳定的电压,导致采样周期在一定范围波动,因此可认为系统式(1)的采样周期为hk=Δhk+h,其中,Δhk为扰动时间参数,并且采样周期满足δ0≤hk≤δ1,δ0,δ1为正整数。针对这种情形,有以下结论。
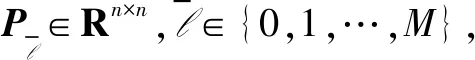

(14)
对所有l∈{0,…,M-1},r∈{2,N},l,s∈{0,1}成立,则二阶多智能体系统式(1)实现二阶一致。
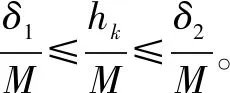
3.2 关于系统参数的鲁棒性
考虑扰动对系统参数的影响,则系统式(1)可建模为如下参数不确定性的二阶多智能体系统
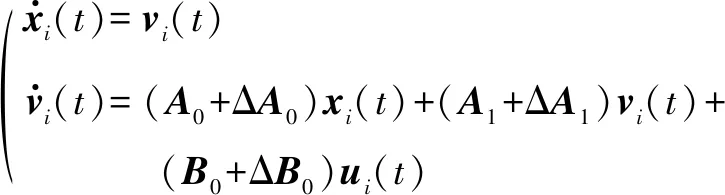
(15)
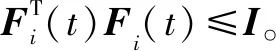
闭环系统式(3)和式(15)可写成紧凑形式
(16)
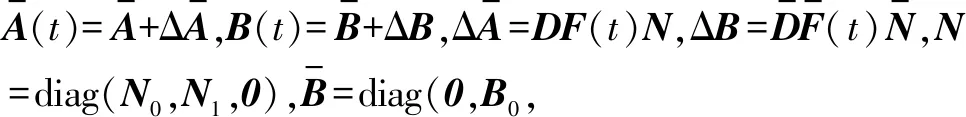
系统式(15)的鲁棒一致性判据如下。
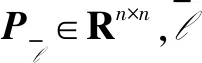
(17)
(18)

证明。利用凸组合技术,式(17)~(18)可导出

(19)
(20)
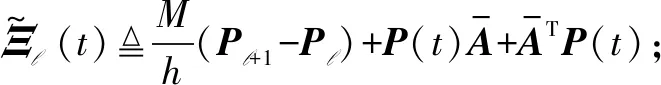
选取定理1中2)证明的拟周期Lyapunov函数V2(t),利用引理2计算其求导
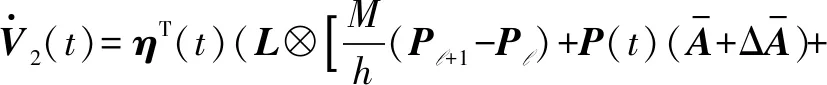
(21)

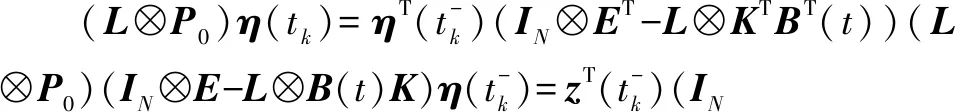

注2:不同于现有仅适用于单输入单输出系统的根轨迹收敛性分析方法,例如文献[9-13],本文采用拟周期Lyapunov函数方法不仅解决了多输入多输出二阶多智能体系统的脉冲一致性问题,而且解决了非周期采样和参数不确定的二阶多智能体系统的鲁棒脉冲一致性难题。同时,以低维数(不依赖多智能体数量)的线性矩阵不等式给出了能够实现鲁棒一致性的判别准则。
4 数值仿真
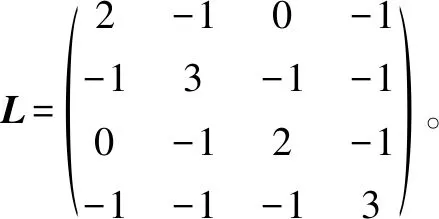
1) 例1。
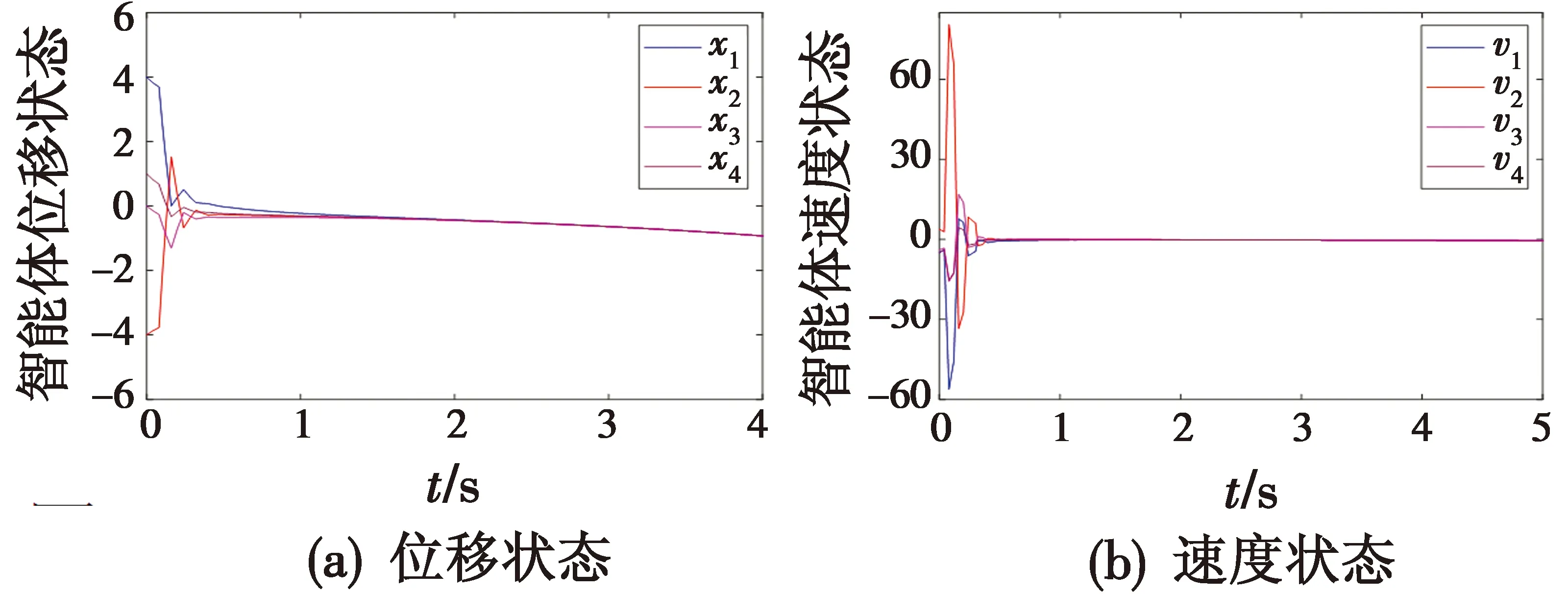
对于给定的采样周期h=0.08 s,根据定理1计算状态转移矩阵的谱半径ρ(Ψ(h))=0.927 3,即该系统实现二阶一致。随机给定初始值,所有智能体的位移状态和速度状态如图1所示,可见智能体的状态分量分别趋于一致。
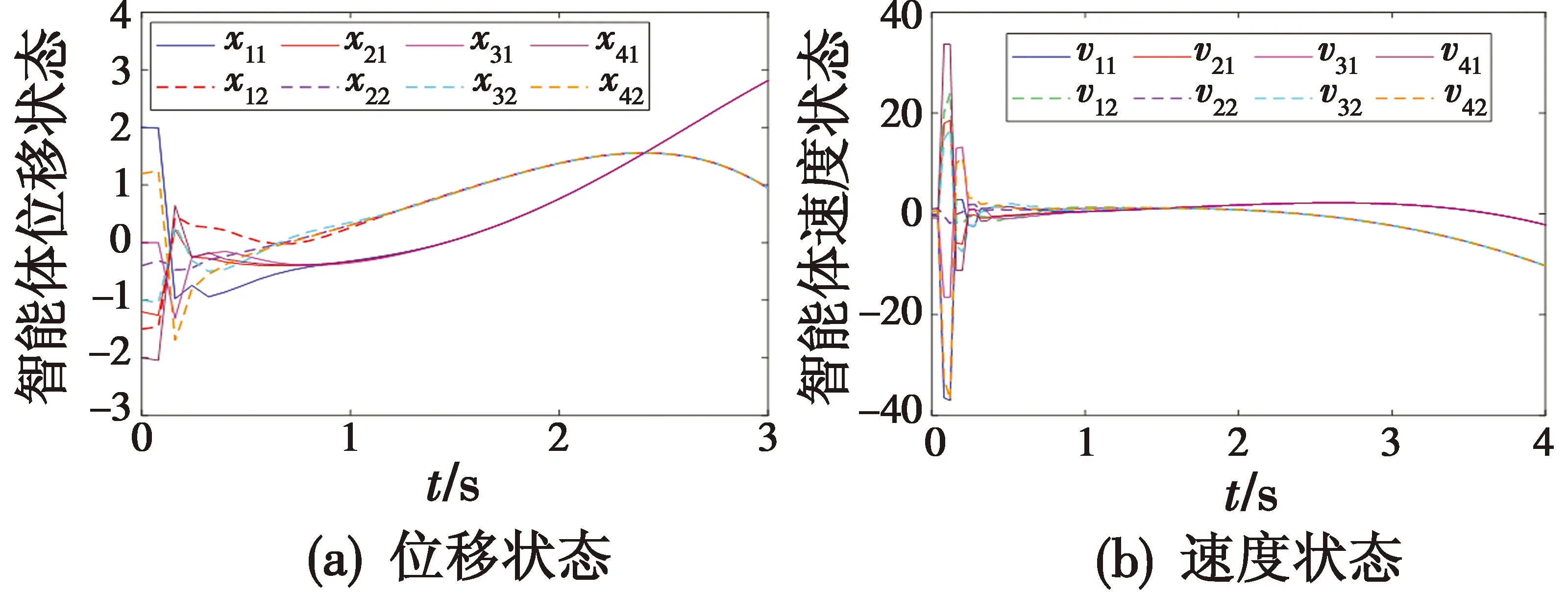
图1 例1:多智能体系统式(1)位移和速度状态
2) 例2。
针对系统式(13),选取控制器增益K1=3.6,K2=-3,根据推论1求得采样周期满足0 s 图2 例2:多智能体系统式(13)位移和速度状态 3) 例3。 设系统式(15)参数为:A0=2,A1=-5,B0=1,D0=0.1,D1=0.2,D2=0.3,N0=-0.1,N1=-0.2,N2=0.4,F0(t)=sin 5πt,F1(t)=cos 1.5πt,F2(t)=sin 3πt。选取控制增益K1=4.6,K2=-3.7。根据定理3,选取ε=ε0=0.1以及M=3,求解矩阵不等式(17)~(18),得到采样周期为h=0.08 s。随机给定初始值,所有智能体的位移和速度响应如图3所示,最终每个智能体的状态曲线趋近重合,实现二阶一致。 图3 例3:多智能体系统式(15)位移和速度状态 本文针对一般高维线性二阶多智能体系统,设计了仅含采样位移信息的分布式脉冲一致性控制算法。利用谱分析和拟周期齐次Lyapunov函数方法,建立了一系列能够实现二阶一致性的判据,分析了所提脉冲一致性算法对范数有界的不确定采样周期和系统参数的鲁棒性,并以低维数的线性矩阵不等式给出了能够实现鲁棒二阶一致性的条件。将本文的建模与分析方法推广到含有测量噪声、网络攻击以及切换拓扑的二阶多智能体系统是未来的研究方向。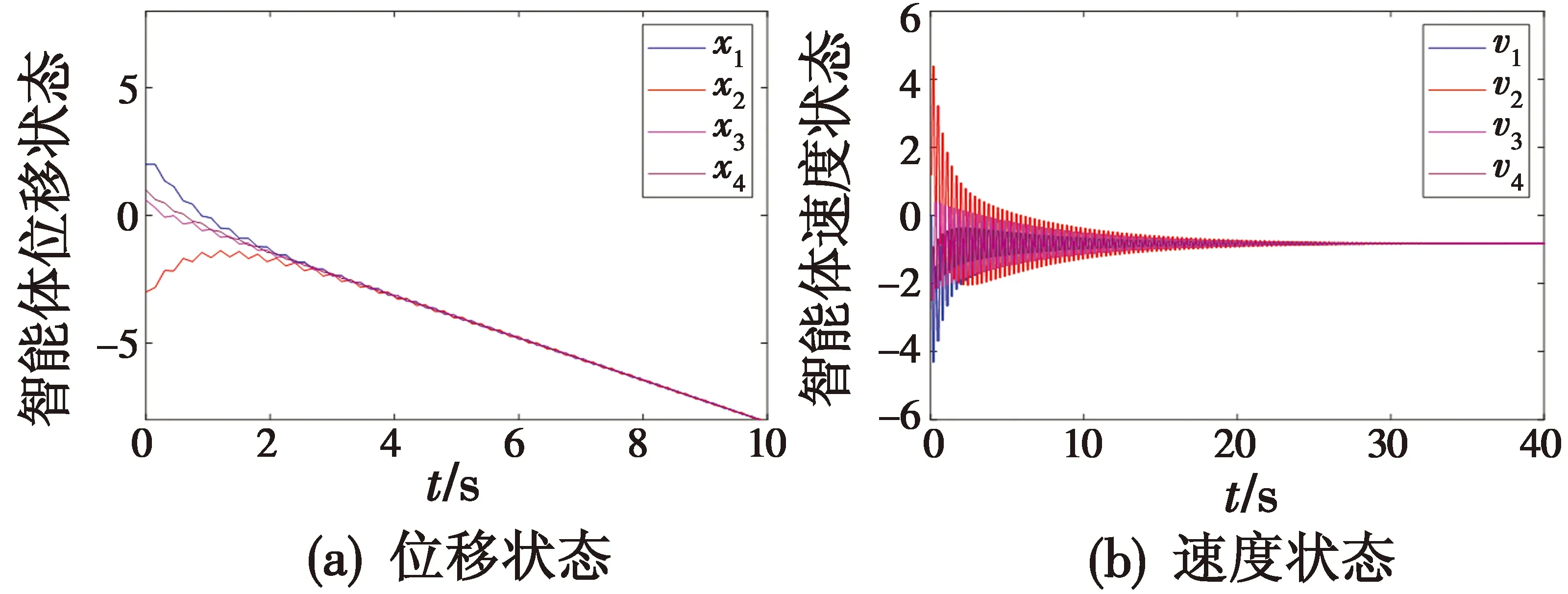
5 总结
