未知输入下多智能体系统的分布式协同控制
2023-10-25翁凯,任彦,高伟
翁 凯, 任 彦, 高 伟
(内蒙古科技大学,内蒙古 包头 014000)
0 引言
近年来,多智能体系统(MAS)协同控制已广泛应用于军事、能源、医疗、通信等各个方面[1-5],尤其在航空航天军事领域,对于领弹-从弹系统协同制导问题的研究也成为热点[6-8]。
在解决领弹-从弹系统协同制导问题时,可以将各导弹看作质点,以质点的加速度为控制输入,将其制导过程简化为基于位置和速度的领导-跟随二阶多智能体模型[9],领弹和从弹分别为多智能体系统的领导者和跟随者,通过设计合适的制导控制律使制导系统实现对同一个目标的快速精准打击。这样便将上述问题转化为领导-跟随MAS的分布式协同控制问题。
一致性问题是研究MAS协同控制的基础。文献[10]针对时滞线性变参数模型的领导-跟随MAS的一致性问题,给出了使系统达到渐近鲁棒一致性收敛的滑模控制协议;文献[11]提出了在时变时延和成本约束下MAS的渐近收敛一致性控制协议。而传统的渐近收敛存在收敛速度慢、抗干扰能力较弱等缺点,有限时间一致性控制理论的出现有效地解决了上述问题。文献[12]针对具有外部有界干扰的二阶无领导者MAS分布式一致性控制问题,设计了新型有限时间一致性协议;文献[13]针对智能体间通信权值的变化,设计了一种基于有向通信拓扑的领导-跟随有限时间一致性协议。
然而,各智能体在达到一致性的过程中,会受到通信延迟、节点内部动力系统和建模误差等不确定因素的干扰,而使系统的动态性能和稳定精度受到不利影响[14]。目前为了解决这些问题,广泛使用滑模控制来提高系统的鲁棒性和准确性[15]。文献[16]结合有限时间理论,提出了一种基于非线性积分滑模控制的有限时间一致性控制算法;文献[17]针对二阶扰动系统,提出了一种新的非奇异有限时间终端滑模控制方法;文献[18]提出了非线性积分滑模控制方法,有效地消除了抖振,实现了有限时间收敛。
在领导-跟随二阶MAS中,若能获得领导者速度的微分信号(即控制输入信息),则可以得到更好的控制效果,然而在实际中却难以获取,很多文献都是假设领导者控制输入信息已知或为零[19]。为了保证微分信号的品质,文献[20]提出了非线性跟踪微分器的概念;再将有限时间思想结合到跟踪微分器的设计中,可以进一步提高微分器性能[21]。文献[22]设计了一个有限时间跟踪微分器来获取平滑的位置信号及其导数;文献[23]提出了基于有限时间非线性微分器的测速方法,能够较为精准地获取速度信号。
受前人工作的启发,本文首先针对未知领导者控制输入信息情况下的二阶MAS,设计了基于双曲正切函数的有限时间跟踪微分器来获取领导者的控制输入信息;然后设计了新型变速趋近律,其中减速点的引入提高了系统的动态性能,在此基础上构造了一致性控制律,以实现系统在有限时间内快速准确的一致性跟踪控制;最后,将上述所提算法应用于领弹-从弹系统的协同制导,并通过仿真验证了本文所提算法的有效性。
1 预备知识与问题描述
1.1 图论
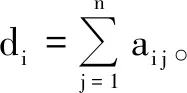
引理1[24]设L是一个有向图G的拉普拉斯矩阵,如果G存在一个生成树,那么L有且仅有一个零特征值,其他特征值均有正实部。
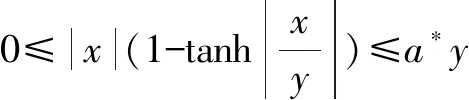
1.2 系统建模
考虑具有一个领弹和n个从弹的制导系统,领弹的运动学模型为
(1)
式中,x0,v0,u0分别是领弹的位置信息、速度信息和控制输入。制导系统第i个从弹运动学模型为
(2)
式中,xi,vi,ui分别为从弹i的位置信息,速度信息和控制输入。
定义1系统式(1)和式(2)实现一致性跟踪需满足
(3)
2 理论结果
2.1 双曲正切有限时间跟踪微分器的设计
有限时间跟踪微分器(Finite-time Tracking Differentiator,FTD)能满足工程上在有限时间内提取微分信号的性能要求,且对信号有较准确的估计,能减少抖振现象[26]。设计跟踪微分器的核心为加速度函数的选取,其决定了跟踪微分器的性能好坏。加速度函数需要在状态接近平衡点时具有近似线性的特性来保证系统收敛的平滑性,在远离平衡点时具有饱和非线性的性质以保证收敛的快速性。
本文选取符合上述条件的双曲正切函数设计了如下形式的FTD
(4)
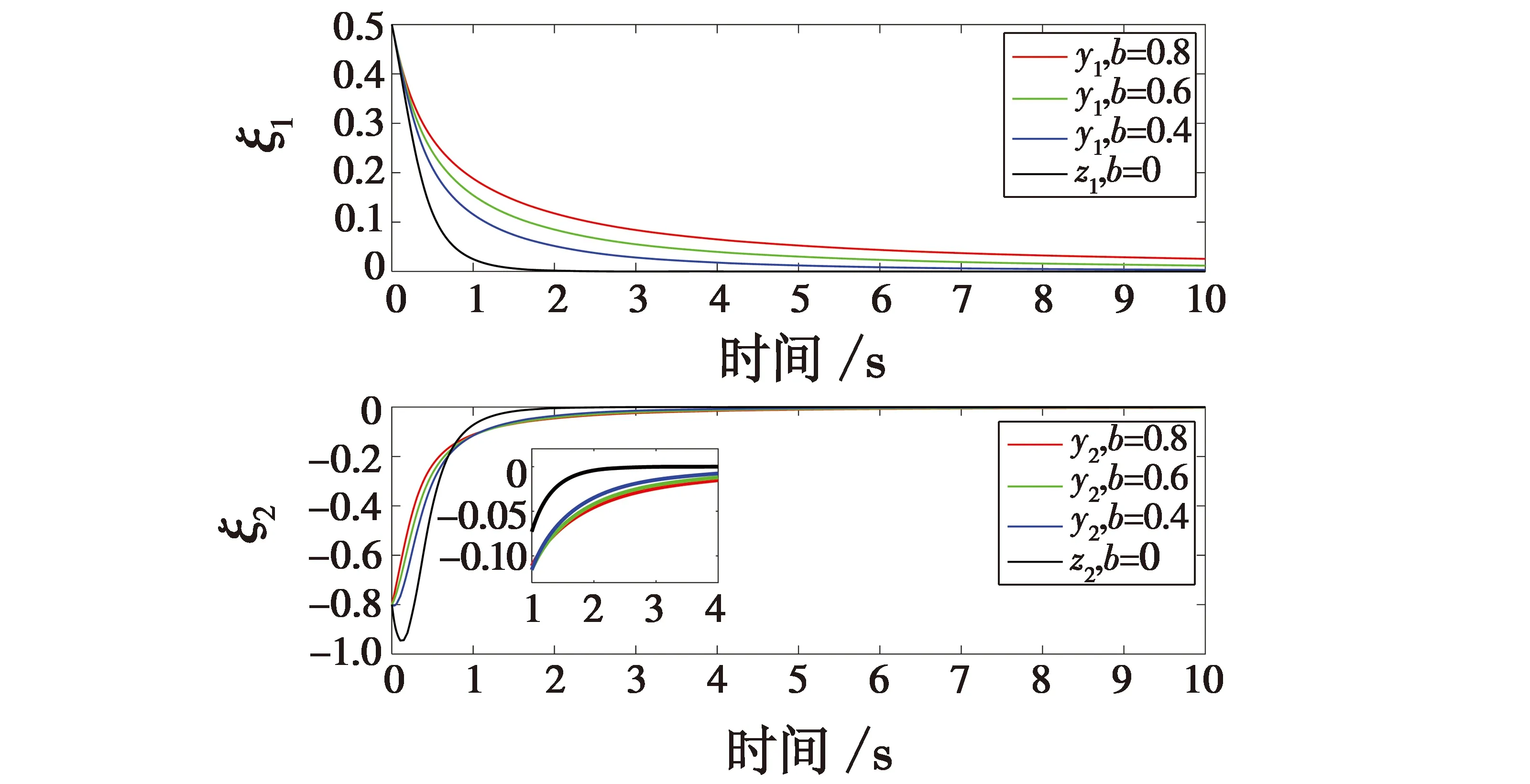
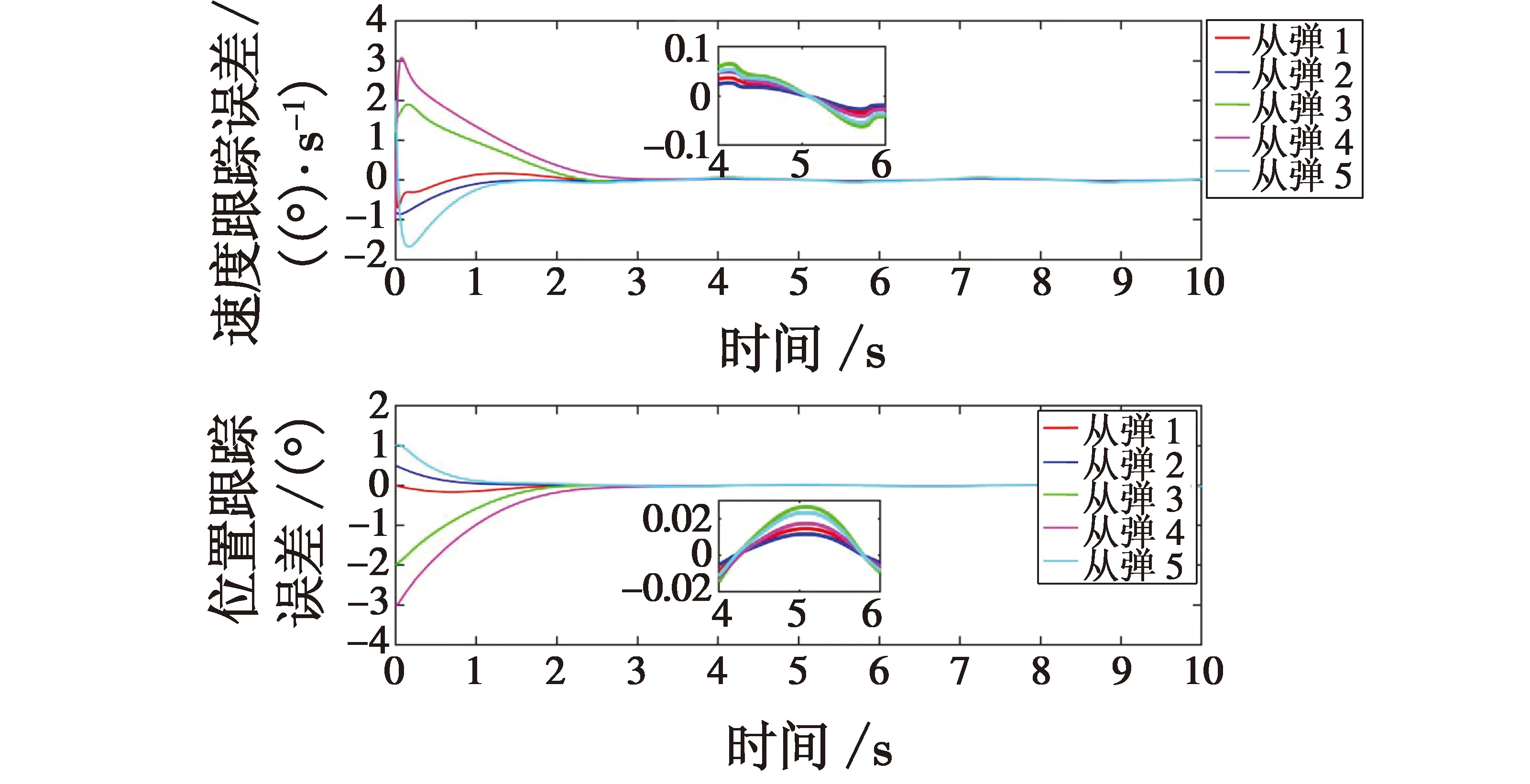
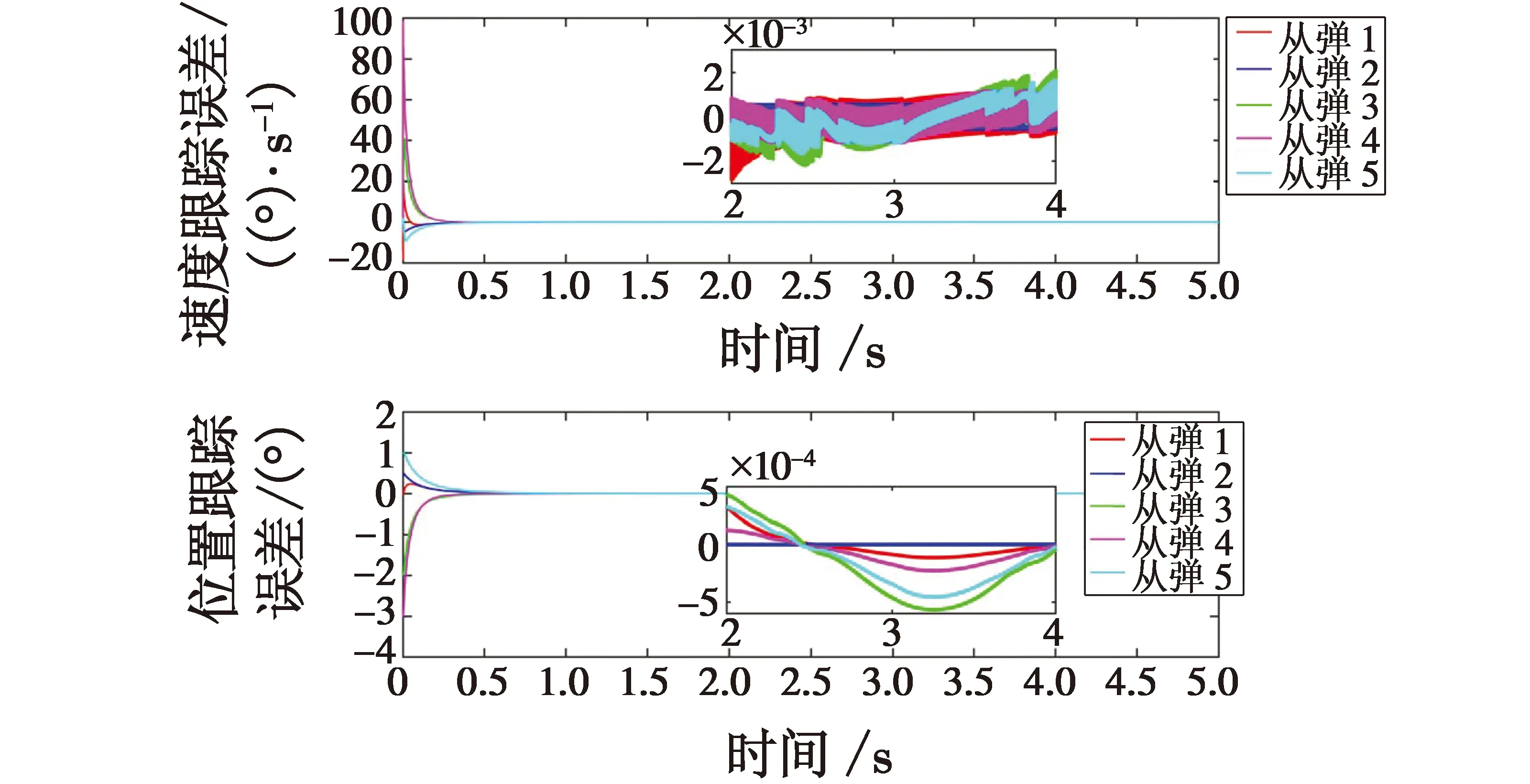
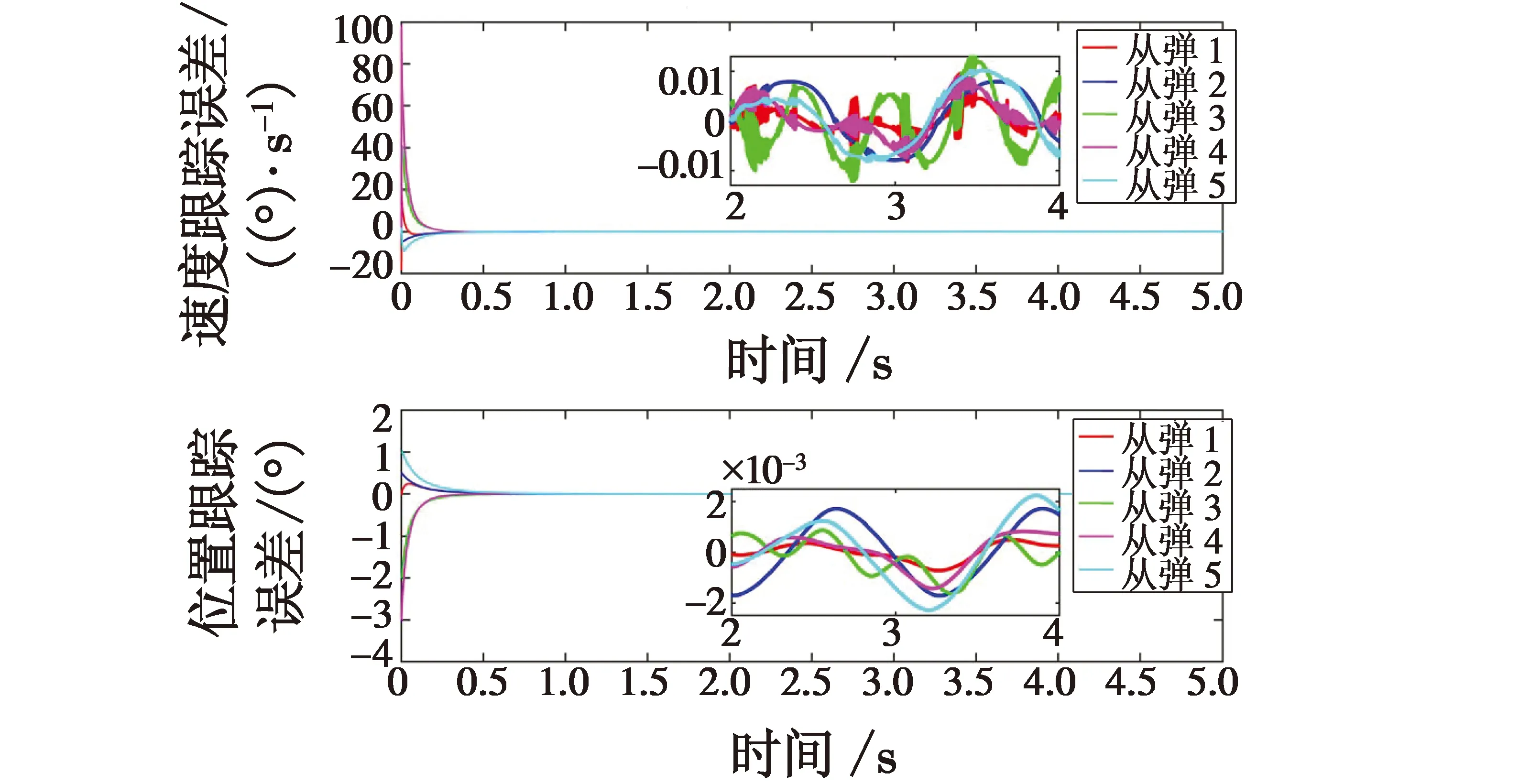
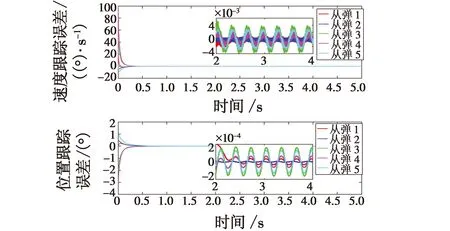
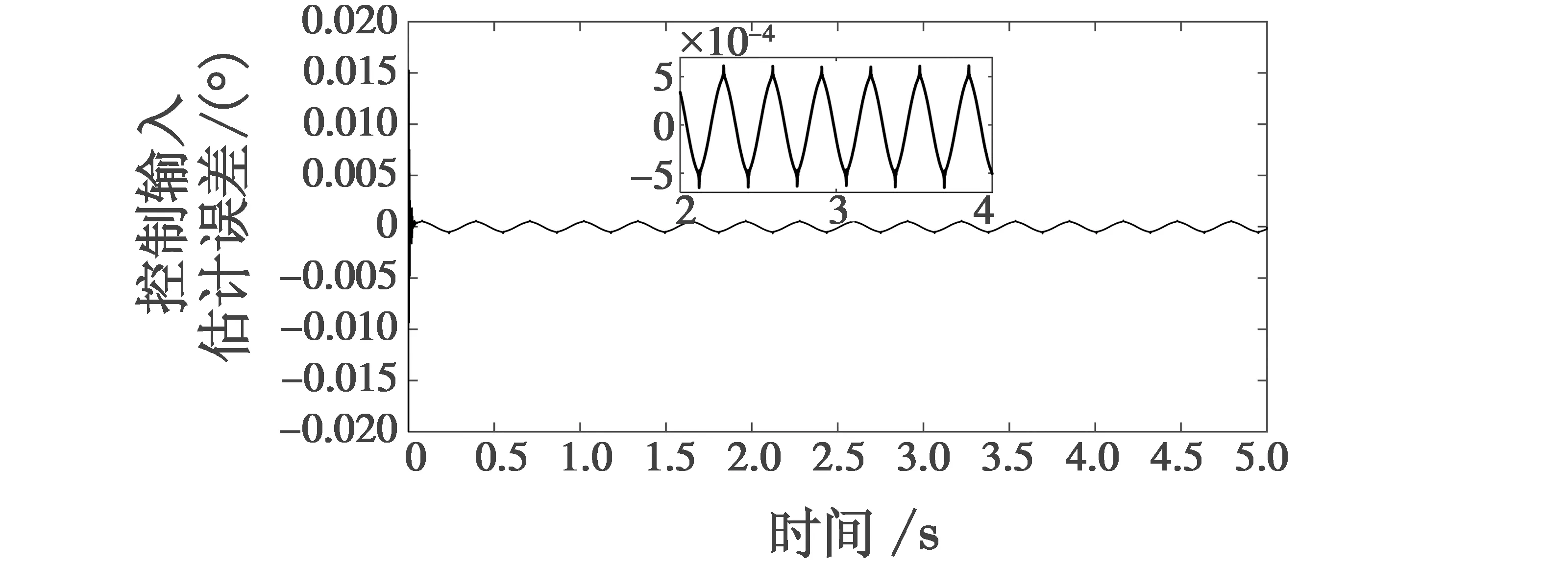
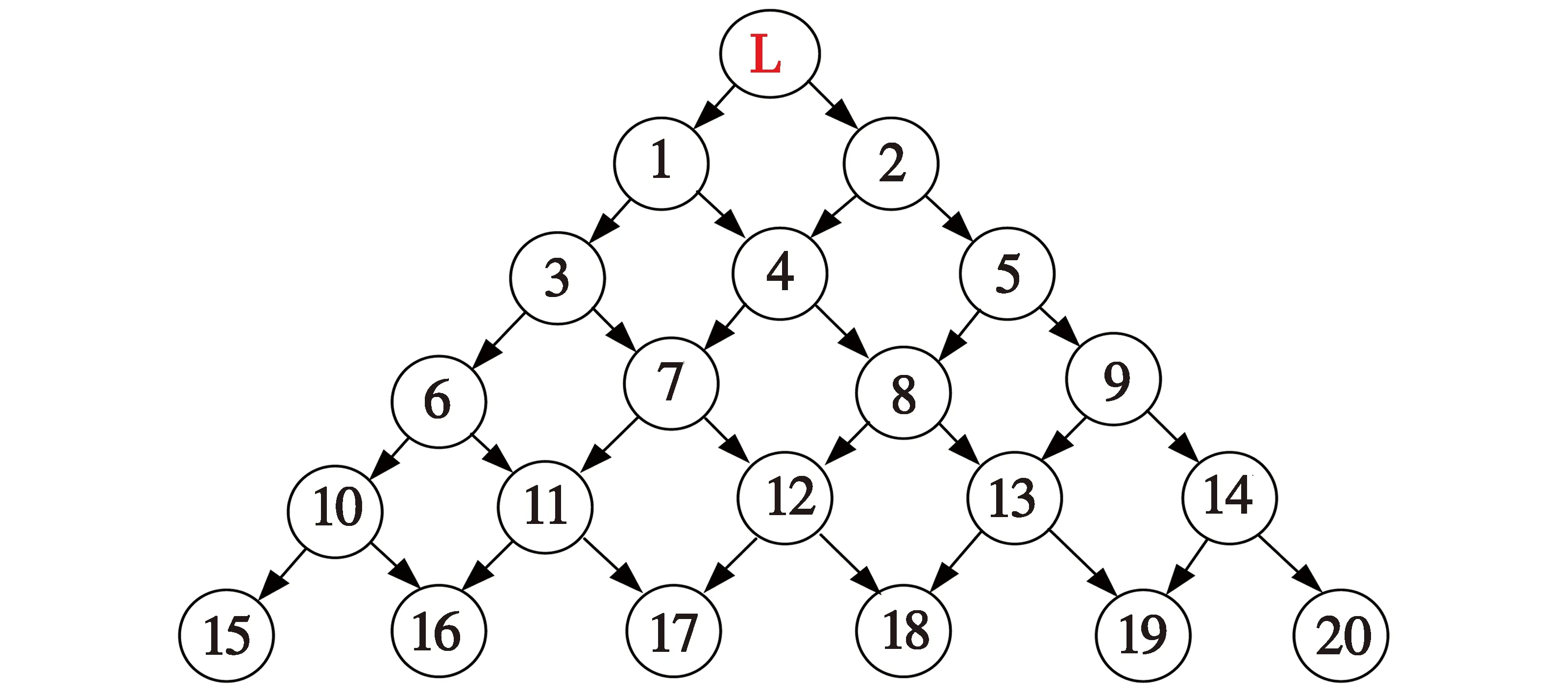
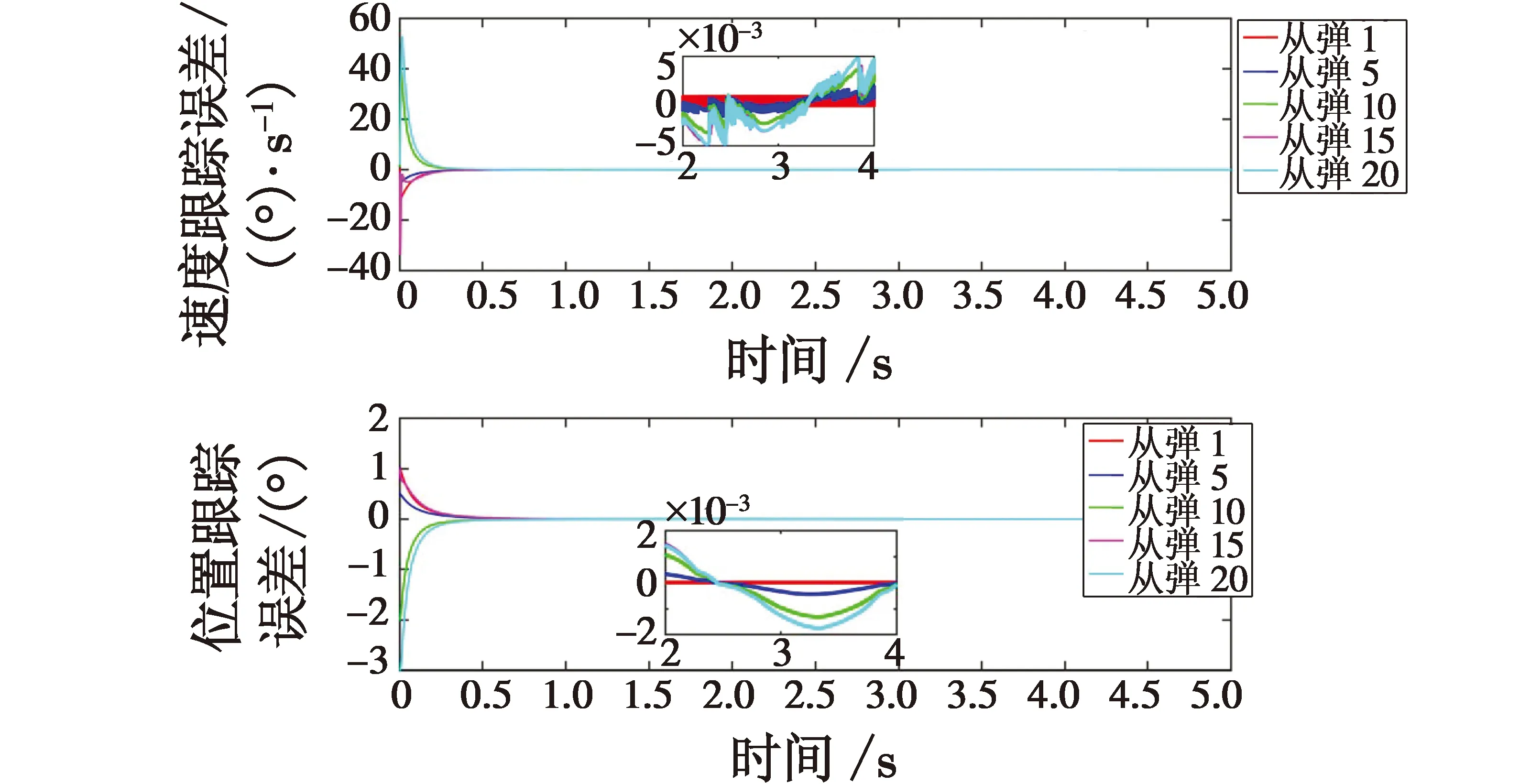
式中:a1>0;a2>0;R>0;0 图1 系统状态收敛过程 由图1可以看出:当状态离原点(0,0)较远时,y2比z2收敛更迅速;当状态接近原点(0,0)时,y1,y2较z1,z2收敛速度放缓,可以更好地削弱微分器输出高频抖振,且b取值越大,对噪声的抑制能力越强,但是状态收敛精度也会有所下降。因此,针对实际系统选择参数时,通过微调b的取值能够综合考虑抖振和收敛精度的影响,使系统获得更均衡的性能。 引理3[29]考虑如下系统 (5) (6) 定理1考虑上述设计的式(4)FTD,选择合理的参数R,a1和a2,则ξ1能在有限时间T内精确跟踪输入信号v0,从而ξ1的微分ξ2可以跟踪输入信号的微分。 证明。定义FTD的跟踪误差 (7) 对式(7)进行求导 (8) (9) (10) 选取李雅普诺夫函数 (11) (12) 由式(11)可知 λmin(P)‖ψ‖2≤V≤λmax(P)‖ψ‖2 (13) (14) 因此, (15) 由式(15)可得 (16) (17) 由式(17)可推出 (18) (19) (20) 由式(18)得,当0≤t≤T时,V≤V(0),因此eη和eω在(0,T)内有界,即 (21) (22) 为了提高系统的协同跟踪控制能力、提高跟踪速度和跟踪精度,结合有限时间理论,设计了基于新型变速趋近律的有限时间一致性跟踪控制律,使滑模面在有限时间内快速收敛至平衡位置,实现了快速稳定跟踪,且具有很强的鲁棒性。 根据上述有限时间跟踪微分器以及领弹-从弹系统的运动学模型,定义跟踪误差为 (23) 令Ex=[ex1…exn]T,Ev=[ev1…evn]T,则系统的误差动态方程可以改写为 (24) 式中:H=L+B;1n为所有分量为1的n维列向量;U为制导系统的控制律;u0为领弹的控制输入。 引理4[29]考虑如下系统 (25) (26) 为了提高系统的跟踪精度和响应速度,基于系统模型式(1)和式(2)、跟踪微分器式(4)和跟踪误差式(7),设计以下非奇异终端滑模面 S(t)=Ex+k1sigα1(Ex)+k2sigα2(Ev) (27) 式中:k1>0;k2>0;1<α2<2;α1>α2;sig(·)为Sigmoid函数。 对式(27)进行求导,并将式(24)代入,可得S(t)的导数为 (28) 常用的快速幂次趋近律表达形式为 (29) 式中:S为滑模变量;γ1>0;γ2>0;0<β<1。 针对以上问题设计以下变速趋近律 (30) (31) 其中:η>0;0<δ0<1;0 由以上分析可知,参数γ2的取值大小会影响系统瞬态收敛的性能。若γ2取值较小,则收敛速度较慢,若γ2取值较大,则会带来一定的抖振问题。所以引入文献[30]的思想,构成新型变速趋近律 (32) (33) χ(S)=tanh(ξ(|S|-μ))+1 (34) 其中:χ(S)为辅助函数,用以调节滑模变量的收敛速度;μ为减速点,满足0<μ<1;ξ>0。当ξ=100,减速点μ设置为0.1时,χ(S)的函数曲线如图2所示。 图2 χ(S)函数曲线 为了验证改进后的新型变速趋近律式(32)的有效性,在滑模面式(27)条件下,分别与一般幂次趋近律 (35) 以及快速幂次趋近律式(29)、变速趋近律式(30)进行仿真对比。滑模变量S动态曲线如图3所示。由图3可知,新型变速趋近律式(32)的收敛速度快,且在接近滑模面处对滑模抖振的抑制有不错的效果。因此,基于此趋近律所设计的控制律可以提高收敛速度和跟踪精度,进而提升系统一致性跟踪控制的能力。 图3 滑模变量S动态曲线 由滑模面式(27)、趋近律式(32)构建领弹-从弹系统的一致性跟踪控制律为 (36) 定理2考虑系统式(25),选择滑模面式(27)、趋近律式(32),当在此滑模面上采用控制律式(36)时可以保证系统实现有限时间一致性跟踪控制。 证明。定义Lyapunov函数 (37) 对式(37)进行求导,并将式(28),(36)代入得 (38) 进而可得 (39) (40) 根据引理4可知,S在有限时间t1内收敛至零,同时,制导系统可以实现有限时间一致性,收敛时间为 (41) 为了验证本文所提方法的合理性与有效性,进行以下仿真实验。领弹和从弹的状态分别由式(1)与式(2)来描述,假设仿真实例中的系统拓扑图如图4所示。 图4 领弹-从弹系统有向拓扑图 假设动态领弹(L)初始状态x0(0)=1°,v0(0)=0 (°)/s(单位下同),动态领弹控制输入为 u0=2cos 2t。 (42) 为了验证本文算法的优越性,选取不含滑模结构的一般性控制律U1[31]和基于一般幂次趋近律式(35)的滑模控制律U2进行对比,即 U1=-k′1sigα1(Ex)-k′2sigα2(Ev) (43) (44) 假设从弹的初始状态为x(0)=[1 1.5-1-2 2]T,v(0)=[0.5-0.8 1.2-12]T。参数设置为:k′1=35,k′2=25,k1=100,k2=2,α1=2,α2=3/2,γ1=10,γ2=20,β=0.1,ξ=900,μ=0.001,p=0.8,Ψ=2,δ0=1/8,a1=60,a2=10,b=0.6,R=200。 控制律式(43)和式(44)的状态跟踪误差如图5、图6所示。 图5 控制律式(43)系统状态误差 图5中速度误差和位置误差分别是0.1 (°)/s和0.03°,稳定时间分别为5 s和4 s;图6中速度误差和位置误差分别是0.02 (°)/s和3×10-3(°),稳定时间均为9 s。由此可见,以上控制律的收敛速度较慢,跟踪精度较低。 图7所示为领弹的控制输入与跟踪微分器式(4)估计的控制输入之间的误差,可以看出跟踪精度为6×10-5(°)/s,这说明跟踪微分器式(4)能够快速准确地估计领弹的控制输入。图8显示了采用控制律式(36)时的系统状态跟踪误差,可以看出速度误差和位置误差分别是3×10-3(°)/s和6×10-4(°),速度和位置趋于稳定的时间均为2 s。通过图5、图6和图8的对比结果可以看出,基于本文提出的新型变速趋近律所构造的控制律式(36)能够更快、更准确地实现制导系统的一致性跟踪控制。 图8 控制律式(36)系统状态误差 为了进一步验证该制导控制律在复杂战场环境下的优越性,分以下3种情况进行讨论和仿真。 1) Case 1。考虑多导弹制导系统在实际制导过程中,各导弹不可避免地会受到干扰,如空气摩擦的影响、导弹自身重力的影响或其他外部干扰的影响等,这不仅会影响各导弹的正常飞行,而且可能会阻碍制导系统协同精准打击目标的实现。考虑到这些扰动的影响,加入如下形式的有界扰动 (45) 各从弹之间的状态误差如图9所示。其速度误差和位置误差分别是0.01 (°)/s和2×10-3(°),稳定时间均为2 s,可以看出,控制律式(36)具有良好的鲁棒性,在受到干扰的情况下系统仍能快速、精准地实现一致性跟踪控制。 图9 控制律式(36)系统状态误差(Case 1) 2) Case 2。考虑到制导系统在执行某项特定打击任务时可能会通过频繁调整飞行的加速度进而达到既定的飞行状态,所以要求跟踪微分器能够跟踪频率更高的输入信号。将领弹的控制输入改为u0=2cos 20t,即领弹的输入信号的频率变高,其他参数保持不变。图10显示了采用控制律式(36)时的系统状态跟踪误差,其速度误差和位置误差分别为5×10-3(°)/s和2×10-4(°),稳定时间均为2 s。图11是领弹的控制输入与跟踪微分器式(4)估计的控制输入之间的误差,为6×10-4(°)。由此可得,在领弹控制输入频率较高的情况下,跟踪微分器式(4)仍能快速、准确地估计输入信号,从弹仍能精准、快速地跟踪领弹的输入。这表明所设计的有限时间跟踪微分器式(4)和控制律式(36)具有良好的性能。 图10 控制律式(36)系统状态误差(Case 2) 图11 领弹控制输入误差(Case 2) 3) Case 3。考虑到一个多导弹攻击集群在执行某项特定打击任务时可能会由1枚领弹带领多枚从弹进行打击,所以需要协同制导律能够在此情况下使从弹精准、快速地跟随领弹的速度和位置,以达到对目标的一致性打击。图12是由1枚领弹与20枚从弹组成的制导系统有向拓扑图,图13是在此情况下等间隔抽取5个从弹的状态误差图。速度和位置的跟踪误差分别是5×10-3(°)/s和2×10-3(°),稳定时间均为2 s。由此可得,在从弹数量增多的情况下,控制律式(36)仍然可以保证使系统快速、精确地收敛。 图12 领弹-从弹系统有向拓扑图(Case 3) 图13 控制律式(36)系统状态误差(Case 3) 针对领导-跟随二阶MAS,研究了有限时间分布式协同控制问题,并将其应用于领弹-从弹系统的协同制导控制方案中。为了获得领弹的控制输入信息,提出了一种基于双曲正切函数的有限时间跟踪微分器,然后结合新型变速趋近律设计了跟踪控制律,使制导系统实现了有限时间一致性,并给出了跟踪微分器和一致性控制律的理论分析结果,用以证明其可行性。考虑制导系统在实际运行中存在的干扰以及带领从弹数量增多的情况,仿真结果表明,所设计的控制律具有良好的鲁棒性和跟踪效果;在领弹控制输入频率较慢和较快两种情况下,所设计的跟踪微分器和控制律仍然具有良好的性能。
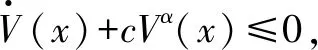
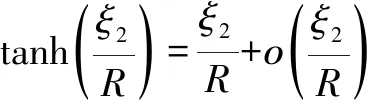
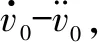
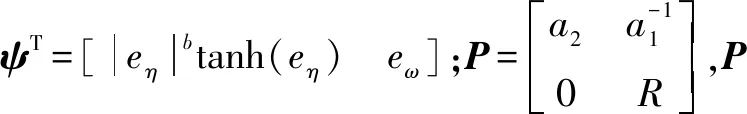
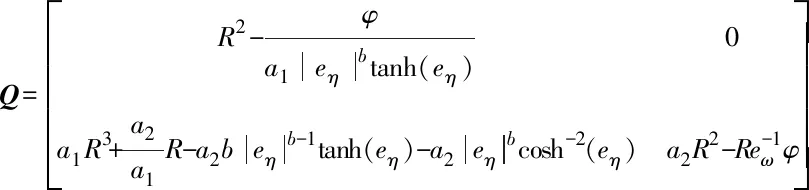
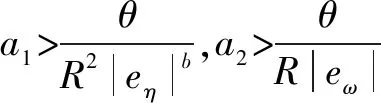
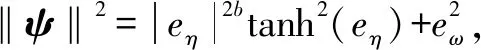
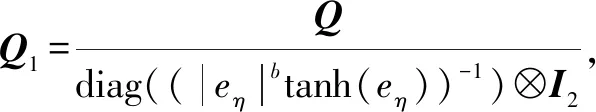


2.2 基于新型变速趋近律的一致性跟踪控制
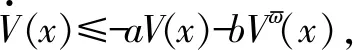
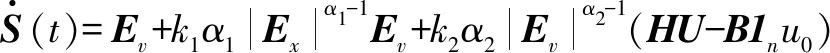
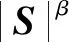




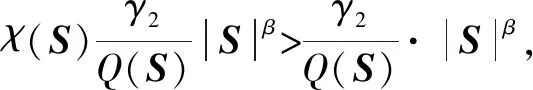
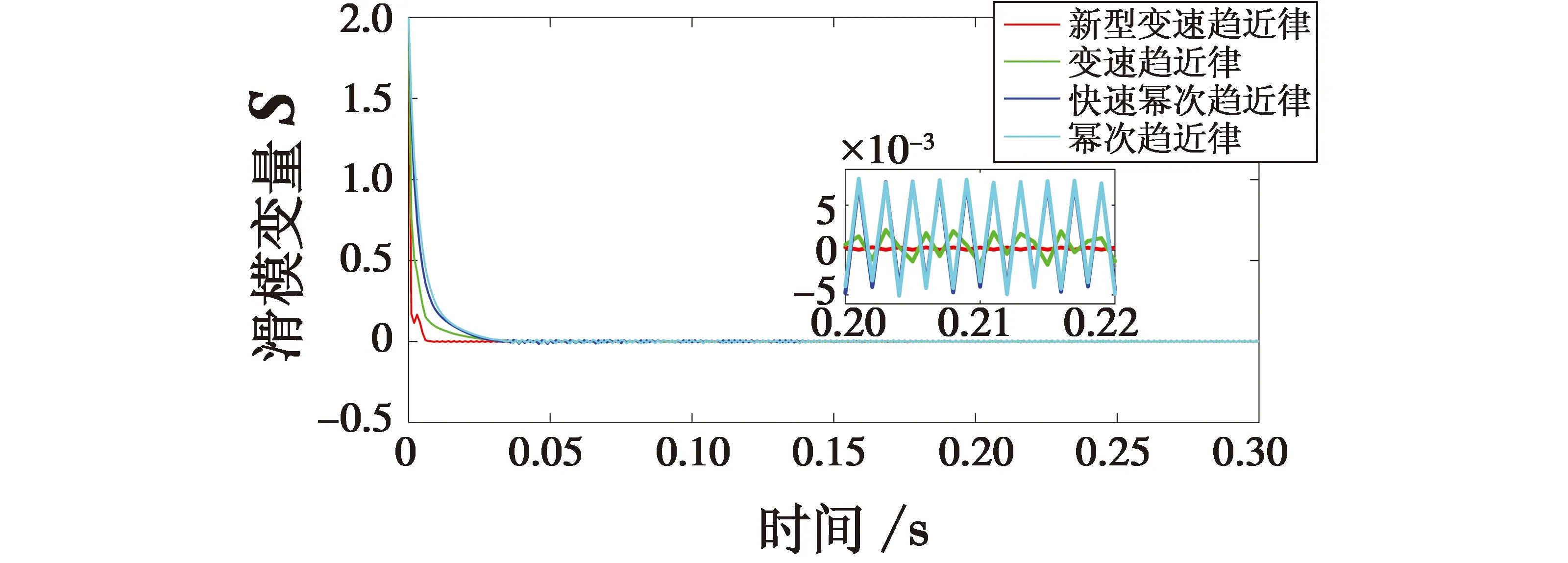
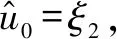
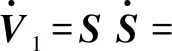
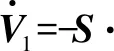


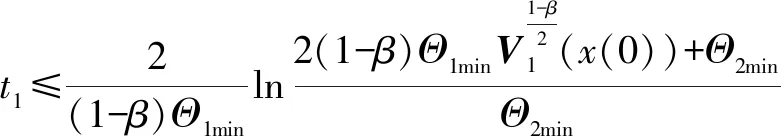
3 仿真实验与结果分析

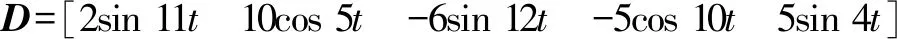
4 结束语
