基于异构计算平台的背景噪声预处理并行算法*
2023-10-24周俊伟李会民孙广中
吴 超,卫 谦,周俊伟,李会民,孙广中
(1.中国科学技术大学网络信息中心,安徽 合肥 230026;2.中国科学技术大学物理学院,安徽 合肥 230026;3.中国科学技术大学地球和空间科学学院,安徽 合肥 230026;4.中国科学技术大学计算机科学与技术学院,安徽 合肥 230027)
1 引言
传统的地震学研究采集天然或人工震源产生的地震波信号,利用地震波反演地质结构信息。地震台站观测的波形信号除了地震信号,还包含大量的背景噪声。通常认为背景噪声是无价值的信号,在资料处理中应予去除[1]。近年来随着跨学科交叉研究的进展,地球物理学家发现通过计算地震台站间的背景噪声互相关函数NCF(Noise Cross-correlation Function)可以提取出台站间的格林函数[2],进而研究地壳的速度、结构等信息。21世纪以来基于背景噪声的地震学研究得到蓬勃发展[3],相关成果已广泛应用于地球内部结构研究[4]、浅地表地质调查[5]和油气勘探等诸多领域。
然而,直接利用2个地震台站的噪声记录进行互相关计算,通常很难得到高信噪比的格林函数。这主要是由于噪声的频谱存在优势频率,其较强的能量抑制了其它频段的信号。为了减轻这种不利因素的影响,需要对原始背景噪声记录进行预处理,通过时域和频域信号处理,提升特定频段的信噪比,之后进行互相关计算获得所需的信息[6]。
近年来,世界主要大国纷纷加大密集台阵的布设(如美国的USArray和中国地震科学台阵探测计划ChinArray)。这些观测台阵通常由成百上千个观测台站组成,对地震波形进行长年累月的观测积累。密集的地震观测台站和长程的时间积累记录下海量的地震波形数据,结合背景噪声互相关计算,可以反演得到高精度的地下结构图像。与之对应地,获取密集台站间NCF所需的计算耗时也快速增长。为解决数据量激增带来的计算压力,研究人员尝试数据并行路线,采用云计算加速地震数据处理,并取得了一定的成果[7]。随着图形处理器GPU(Graphics Processing Unit)、现场可编程逻辑门阵列FPGA(Field-Programmable Gate Array)等异构计算设备的发展和日益成熟,异构计算设备提供了远高于中央处理器CPU(Central Processing Unit)的数值计算能力,异构并行计算技术为加速地震数据处理提供了新的技术选择。
本文基于GPU异构计算平台设计了地震噪声数据预处理的并行优化方法。
2 相关工作
2.1 NCF计算方法
在背景噪声地震学研究中,通常将台站与台站之间形成的“台站对”称为路径。N个地震台站两两之间形成的有效路径(以台站A和台站B为例,台站与自身的结对如路径AA和BB去除,头尾对换的2条路径如AB和BA视为等同,只保留其一)数量为N(N-1)/2。NCF计算的主要过程分为3个步骤:
(1)预处理计算:对台站单天的时域信号进行去趋势处理、带通滤波、时域归一化和谱白化等处理得到频谱;
(2)互相关计算:对路径在同一天的频谱进行共轭相乘并经傅里叶反变换得到该路径时间域的NCF;
(3)叠加计算:对路径长时间(根据尺度从小到大,范围可以为周、月、年)的NCF进行叠加求平均得到该路径最终的互相关信息[8]。
3个步骤中互相关计算与预处理计算算法复杂,耗时比较高。预处理部分计算量正比于参与计算的台站个数以及叠加的天数,互相关部分计算量正比于参与计算的台站个数的平方以及叠加的天数。
2.2 NCF并行优化现状
随着密集地震台阵的建设和地震波形数据长时间的积累,计算耗时长的问题逐渐成为NCF应用的一个主要阻碍。以ChinArray为例,据测算其台阵674个台站1年的记录数据(降采样到1 Hz)的NCF计算在1台高性能服务器(Intel®双路Xeon®E5-2620,64 GB内存)上需要耗时3 840 h,接近6个月的时间[9]。为了提升数据处理的计算性能,研究人员尝试采用不同的方法对NCF算法进行优化加速。文献[10]使用云计算技术加速 NCF计算;文献[11]基于分布式内存并行计算机设计了NCF并行算法;文献[12,13]分别实现了Julia语言和Python语言的NCF高性能计算方法;文献[14]提出了CPU-GPU架构超级计算机的NCF的高效计算方法;文献[15]描述了在统一计算架构CUDA(Compute Unified Device Architecture)上实现NCF计算的方法。上述研究都选择NCF计算中计算复杂度最高的互相关计算部分进行优化,对预处理计算的加速优化则没有涉及。由于预处理算法的多样性和可变性,在实际的工程实践中预处理计算实施的次数通常远高于互相关计算;同时,随着高频地震信号(如10 Hz~100 Hz)的测量和分析,预处理计算的数据规模也呈数量级增长。因此,作为NCF计算的热点问题之一,预处理计算同样具备性能优化的必要性和价值。
2.3 CUDA并行计算
统一计算架构CUDA是英伟达公司为推广CPU+GPU异构计算推出的软件开发包,支持C/C++、FORTRAN等多种编程语言。在CUDA开发环境中,CPU和内存属于主机(host)端,GPU和显存属于设备(device)端。CUDA程序包含host端代码和device端代码,host端代码以逻辑运算为主运行在CPU上,device端以数值计算为主运行在GPU上。通过使用CUDA内置的存储API,实现数据在host和device之间的流动。
CUDA在device端对GPU设备的线程进行多层抽象,经由网格(Grid)-线程块(Block)-线程(Thread)3层结构组织线程。通过规划程序在host端和device端的计算任务,合理使用Grid-Block-Thread组织结构,用户可以充分利用CPU+GPU执行异构计算,获得远超CPU串行计算的运算能力。目前,CUDA并行计算已成功应用于人工智能、科学计算和大数据等诸多应用领域。
3 地震噪声数据预处理串行算法
3.1 算法流程
单台站单天的预处理计算读取台站记录的波形文件作为输入。首先,需对输入的波形数据进行全局去趋势(Detrend)处理;然后,再将波形数据进行分段(Segmentation,分段之间允许有交叠)。对于每个分段的处理,首先是对分段波形(Segment Beam)执行去趋势处理、时域归一化(Time Normalization)处理等时域操作;然后,对分段波形进行快速傅里叶变换FFT(Fast Fourier Transform)得到分段频谱,并对其执行谱白化(Spectrum Whitening)处理;最后,将所有分段频谱(Segment Spectrum)拼接(Concatenate)得到完整频谱,写入频谱文件。预处理计算流程如图1所示。

Figure 1 Serial preprocessing of single-day-beam-file of single station
多台站多天的预处理计算以单台站单天的处理为基础,分别对台站和时间进行两重循环实现对所有文件的遍历处理,如算法1所述。
算法1多台站多天的串行预处理计算
输入:多台站(Nsta)多天(Nday)的波形数据D[]。
输出:多台站多天的频谱数据S[]。
/* 遍历台站 */
1:fori=0 toNsta-1do
/* 遍历天数 */
2:forj=0 toNday-1do
/* 调用单台站单天预处理 */
3:S[i,j]=PreProcess(D[i,j]);
4:endfor
5:endfor
3.2 热点计算函数
3.2.1 去趋势处理
地震波形数据常存在趋势性变化,这种变化可能来自仪器本身的漂移,也可能是地壳蠕变的结果。趋势性变化容易掩盖细微的异常信息,因此在信号预处理中需要进行去趋势处理[16]。
对于时间序列(如地震波形数据)的趋势计算,常用的有3种计算方法:线性方法(基于最小二乘拟合Least Squares Fitting)、非线性方法(基于经验模态分解Empirical Mode Decomposition)和一阶差分法FD(First Differencing)[17]。地震背景噪声预处理采用的是基于最小二乘法拟合的线性方法计算波形趋势。
假设Dn(n=1,2,…,N)是采样间隔为T的均匀采样的波形数据,采样时间t=T,2T,…,NT。Dn包含一阶趋势项a0+a1t,记为式(1):
(1)
基于最小二乘方法拟合出趋势项,如式(2)所示:
(2)
其中,C(N,T)为确定系数,可由求和公式、平方和公式、二阶矩阵求逆得出解析解。由式(1)和式(2)可知,最小二乘法主要的计算量集中在求和∑Di(以及类似计算∑iDi)。朴素的串行求和计算如算法2所示。
算法2朴素串行求和计算
输入:原始波形数据D[],波形点数Npts。
输出:波形数据之和sum。
1:sum=0;
/* 遍历波形数组求和 */
2:fori= 0 toNpts-1do
3:sum=sum+D[i];
4:endfor
求和计算属于归约算法。朴素的串行求和计算通过循环实现,每次迭代将一项元素累加进求和项。前Npts个元素之和依赖前Npts-1个元素之和,实现存在数据依赖关系。
根据式(2)计算趋势项a0+a1t的估计值,波形数据逐项减去趋势项的估计值实现去趋势处理。
3.2.2 时域归一化处理
数据预处理中最重要的一步是时间域归一化处理,其目的是为了去除地震信号、仪器故障引起的畸变信号以及地震台站附近噪声对互相关计算结果的影响。
目前,常用的时间域归一化方法有2种:one-bit方法和滑动绝对平均方法。one-bit方法遍历波形原始记录,将正值替换为+1,负值替换为-1。滑动绝对平均方法则是根据式(3)计算一定时窗内波形数据绝对振幅的平均值,即该时窗中心点的权重,逐段移动时窗,根据式(4)每点的幅值除以权重得到新的波形序列。
(3)
(4)
窗的长度2k+1决定了有多少振幅信息可以保留。当k=0时,滑动绝对平均方法等效于one-bit方法。为计算全部波形数据的时域归一化,下标n从0遍历到Npts-1,在计算过程中当j超过波形数组索引范围时(如j<0或j>Npts-1),超出部分的dj值设置为0进行计算。
本文预处理计算使用滑动绝对平均时域归一化方法,如算法3所示。
算法3滑动绝对平均时域归一化串行算法
输入:原始波形数据D[],波形点数Npts,窗长K。
输出:时域归一化波形数据D[]。
1:k=[K/2];
2:fori=0 toNpts-1do
3:temp=0;
4:forj=0 to 2kdo
5:ifi-k+j≥0 andi-k+j 6:temp=temp+fabs(D[i-k+j]); 7:endif 8:endfor 9:temp=temp/K; 10:D[i]=D[i]/temp; 11:endfor 3.2.3 谱白化处理 谱白化处理利用快速傅里叶变换和反变换,将时域波形的频谱进行分频,对分频波形进行时变增益,最后重新合成获得白化信号[18]。其中的主要计算是快速傅里叶变换。快速傅里叶变换是快速计算序列的离散傅里叶变换或其逆变换的方法。作为信号处理领域的核心算法,已有众多文献讨论FFT算法及实现,FFTW库[19]是其中影响较为广泛的一个实现。本文的串行预处理计算调用FFTW库执行快速傅里叶变换。 本节使用Linux kernel中的系统性能剖析工具Perf对串行预处理计算程序典型计算场景(1 000个波形数据文件,1 Hz数据采样率)的运行时情况进行性能剖析,各计算模块耗时比例如图2所示。 Figure 2 Perf profiling result of serial preprocessing 根据串行预处理程序的性能剖析,主要耗时的计算模块为去趋势处理、时域归一化处理和快速傅里叶变换(谱白化处理)。其中,占比最高的部分为快速傅里叶变换(FFT),达到总耗时的84%;占比第2的是时域归一化处理(Time Normalization),占总耗时的8%;占比第3的是去趋势处理(Detrend),占比4%。3个计算模块总耗时超过95%。I/O时间约占程序整体运行时间的3%左右。 Amdahl定律(Amdahl’s Law)指出:固定计算工作负载的前提下,并行系统随着处理器数目无限增大所能达到的加速比上限为1/Ts,其中Ts为程序中串行分量所占比重[20]。由Amdahl定律可知,仅针对预处理计算耗时最多的快速傅里叶变换模块进行并行加速,并行系统的加速比不会超过8倍。而如果对耗时前三的计算模块进行并行改造,则系统的加速比上限可以达到或接近33倍。为了实现海量波形文件的准实时预处理,尽可能提高系统的加速效果,本文在后续章节中将对预处理程序的所有计算模块进行基于CUDA的移植和优化。 多台站多天的预处理计算是数据密集型任务。密集台阵长时间积累的波形数据容量往往远超单个GPU卡的显存容量,也超出了单台服务器的内存容量。在实际生产环境中,针对计算服务器数量有限,需要使用单台服务器完成密集台阵波形数据的预处理任务的情况,通过采用分批处理的策略完成长时间积累的波形数据在单服务器上的任务计算。分批处理流程如图3所示。 Figure 3 Batch CUDA preprocessing of multi-day-beam-files of multiple stations 分批处理使用二重循环实现。外层循环实现的是硬盘与主机内存的数据(波形数据,算法输入为时域波形,输出为频域波形)传输,在外层迭代计算之前和之后分别执行文件的输入和输出I/O操作。内存循环实现的是主机内存与设备内存的数据传输,在内层迭代之前将数据从主机内存传输到设备内存,在内层迭代之后将数据从设备内存传输到主机内存。对于一次计算任务,需要在主机内存和设备内存之间传输的总数据量是确定不变的,传输次数是影响数据传输开销的主要因素,传输次数越多则传输开销越大。为了减少CPU和GPU之间数据传输次数,分批处理进行迭代的依据是每批处理的波形文件批数以尽量占满主机内存(或设备内存)容量为准,即外层循环的单次迭代处理批数由主机内存可容纳的最大波形文件数确定,内存循环的单次迭代处理批数由设备内存可容纳的最大波形文件数确定。 在对波形文件进行批数划分时,采用针对时间维度的数据划分,设计主机内存、设备内存分层的批处理方法。首先,估算所有台站的单天数据预处理需要的主机内存和设备内存空间。根据服务器和GPU卡的主机内存和设备内存容量,估算主机内存和设备内存单次最多可容纳计算的天数分别为TM和TV(一般有TM>TV)。当遇到主机内存容量小于设备内存容量(TM 在4.1节所述的分批处理流程中,CPU与GPU通过主机内存和设备内存之间的内存拷贝函数实现隐式同步。首先,CPU将GPU需要并行处理的批量波形数据通过cudaMemcpy函数从主机内存传输到设备内存;之后,GPU针对波形数据进行并行处理,得到批量频谱数据;最后,GPU将批量频谱数据通过cudaMemcpy函数从设备内存传回主机内存,完成一轮GPU计算。 CUDA流(Stream)也称异步流,表示GPU操作队列。同一个流内操作的执行顺序是有序的,但每个操作的执行开始时间是不可控的,并且不同流的执行顺序也不能显式控制[21]。为了提升预处理计算的执行效率,通过利用GPU的多流处理能力,将批量处理的数据平均分配到GPU多个流上。不同流数据从主机内存到设备内存的传输、结果从设备内存到主机内存的传输与GPU端的核函数计算可进行并行处理,实现传输延迟的隐藏,减少传输和计算的耗时。多流处理流程如图4所示。 Figure 4 Workflow of multi-stream processing 经由串行程序的静态分析可知,预处理计算的计算任务主要集中在分段波形数据的循环处理,循环中每次迭代处理一个分段的波形数据。由于循环内每个分段的计算独立,分段之间不存在数据依赖或数据竞争,所以单台站单天预处理计算的整个循环可以使用CUDA的一维Grid结构并行处理,每个分段波形数据分配1个Block完成处理。多台站多天的预处理,则是在台站维和时间维进行拓展,使用三维Grid结构完成计算,如图5所示。Grid结构X轴、Y轴、Z轴3个维度分别对应预处理计算处理的分段、台站及时间。 Figure 5 Structure of 3D Grid 单台站单天预处理计算整体的算法如算法4所示。 算法4基于CUDA的预处理并行算法 输入:单台站单天原始波形数据D[]。 输出:单台站单天频域数据S[]。 Step1H2D(Host2Device):波形数据D从内存拷贝到显存。 Step2分配1个Block完成全局波形数据的去趋势处理。 Step3全局波形数据切分成L段,每个分段分配1个Block进行处理。 Step4遍历k从0到L-1,并行处理: Step4.1Block(k)完成第k段波形的去趋势处理、带通滤波和时域归一化处理; Step4.2第k段波形执行快速傅里叶变换,获得分段频谱; Step4.3Block(k)完成第k段波形的谱白化处理。 Step5所有分段频谱拼接成全局频谱。 Step6D2H(Device2Host):频谱数据S从显存拷贝到内存。 基于CUDA实现高效的求和计算是实现去趋势处理的关键。传统的基于相邻元素的归约树并行实现,在相邻的线程之间导致分支发散(Branch Divergence),性能不佳[22]。通过基于可变间隔的规约计算,以及运用共享内存减少访存开销,可实现线程块内高效的并行求和计算,如算法5所示。 算法5单Block求和CUDA核函数 输入:原始波形数据d_data[]和波形点数Npts。 输出:波形数据之和d_sum。 1:inttx=threadIdx.x; 2:inti,stride; 3:doublesum=0; 4:fori=tx;i 5:sum+=d_data[i]; 6:endfor 7:extern_shared_doublepartial[]; 8:partial[tx]=sum; 9:_syncthreads(); 10:forstride=(blockDim.x+1)/2;stride≥1;stride=(stride+1)/2do 11:iftx+stride 12:partial[tx]+=partial[tx+stride]; 13:partial[tx+stride]=0; 14:endif 15: _syncthreads(); 16:endfor 17:iftx==0then 18: *d_sum=partial[0]; 19:endif 基于滑动绝对平均方法的时域归一化处理中波形数据格点的更新是根据周围格点在时间上加权求和得出,本质是一维Stencil计算。Stencil计算是访存密集型计算,使用共享内存缓存格点数据优化程序的访存方式。基于共享内存的时域归一化处理核函数算法如算法6所示。 算法6滑动绝对平均时域归一化核函数 输入:分段波形数据d_data[],分段波形点数Nsegpts,总波形点数Npts,窗长K。 输出:时域归一化分段波形数据d_data[]。 1:inti,j,idx,start; 2:idx=blockIdx.x*blockDim.x+threadIdx.x; 3:tx=threadIdx.x; 4:blkstart=blockIdx.x*blockDim.x; 5:nextblkstart=(blockIdx.x+1)*blockDim.x; 6:_shared_doubled_share[Nsegpts]; 7:d_share[tx]=d_data[idx]; 8:_syncthreads(); 9:doubletmp=0; 10:start=idx-K/2; 11:fori=0;i 12:j=start+i; 13:if(j≥0) and (j 14:if(j≥blkstart) and (j 15:tmp+=fabs(d_share[tx]); 16:else 17:tmp+=fabs(d_data[idx]); 18:endif 19:endif 20:endfor 21:d_data[idx]=tmp/K; 本文的实验平台硬件配置如下:CPU为 Intel®CoreTMI5-7500,架构为Kaby Lake,主频为3.4 GHz,核心数为4,内存大小为16 GB;GPU使用的是NVIDIA的GeForce®RTX 2080Ti,4 352个CUDA核心,双精度浮点性能达到420.2 GFlops,显存大小为11 GB,显存带宽可达616.0 GB/s。 实验方法是针对预处理计算的主要计算模块耗时和程序整体耗时,随着处理波形文件数量的变换,呈现CPU与GPU之间的运行时间和加速比。加速比为CPU运行时间除以GPU运行时间。测试数据为美国地震观测台阵USArray采集的部分波形数据。每个波形文件记录了单个台站单天采集到的地震信号,数据采样率为1 Hz,数据点数为86 400,共有10 000个波形文件。 本文利用NVIDIA公司提供的性能剖析工具中的nvprof软件[23],剖析了基于GPU的并行预处理计算各主要计算模块的运行时性能。图6~图8分别记录了快速傅里叶变换、时域归一化处理和去趋势处理基于CPU的串行和基于GPU的并行版本针对不同数量波形文件的计算耗时。 Figure 6 Runtime of FFT module Figure 7 Runtime of normalization module Figure 8 Runtime of detrend module 快速傅里叶变换模块是串行程序中耗时占比第一的模块。针对数据规模从1 000到5 000个SAC文件,基于GPU的并行版本相比基于CPU的串行版本加速139~203倍。 时域归一化处理模块是串行程序中耗时占比第2的模块。针对数据规模从1 000到5 000个SAC文件,基于GPU的并行版本相比基于CPU的串行版本加速25~30倍。 去趋势处理模块是串行程序中耗时占比第3的模块。针对数据规模从1 000到5 000个SAC文件,基于GPU的并行版本相比基于CPU的串行版本加速58~72倍。 基于CPU的串行预处理计算、基于GPU的并行预处理计算(单流处理)的总处理时间实验结果如表1所示。表中数据是对10次实验取平均得到的结果。 Table 1 Total time costs of preprocessing algorithms 以表1中CPU串行预处理计算耗时为基准,计算预处理计算GPU单流并行和GPU多流并行的加速比,结果如图9所示。 Figure 9 Speedup of parallel preprocessing algorithms 根据实验结果可知:(1) 基于GPU的并行预处理算法性能显著优于基于CPU的串行预处理算法。(2) 随着波形文件数据量的增加,基于GPU的并行预处理算法的加速比呈线性增长,当文件数量达到5 000时,加速比达到最大,约为95.27倍;当文件数量超过5 000时,基于GPU的并行预处理算法的加速比略有下降。原因分析如下:文件数量达到5 000时,GPU计算能力得到充分利用,GPU计算时间与文件I/O时间达到均衡,加速比达到峰值。之后再增加文件数量,由于I/O时间的影响,所以并行系统整体加速比下降。(3)使用多流处理技术,可以隐藏部分数据内存传输的延迟,在单流GPU并行加速的基础上可以进一步获得平均约8%的性能优化效果。 对比传统的基于CPU的串行地震噪声预处理算法,本文提出的基于GPU的并行算法显著提升了计算性能,且具有较好的并行度。通过实验仿真可知,基于GPU的并行预处理算法适用于处理地震波形文件数量较多的场景,为地震数据预处理的GPU加速提供了研究思路。 当前,针对GPU并行模型在地震数据预处理算法中应用的研究文献较少。通过本文实验可知,并行模型对包含大量信号处理计算的地震预处理算法具有良好的加速效果。由于分批处理各批量之间无数据相关性,本文算法非常适于扩展为分布式版本。下一步将研究MapReduce分布式计算框架与本文加速方法相结合的策略,以及研究单计算节点多GPU卡并行计算及多计算节点并行计算在地震噪声预处理算法中的应用。 致谢 感谢中国地震局地球物理研究所王伟涛研究员和王芳博士在本文工作完成过程中给予的指导和帮助。3.3 性能剖析

4 地震噪声数据预处理算法的并行优化
4.1 分批处理

4.2 多流处理
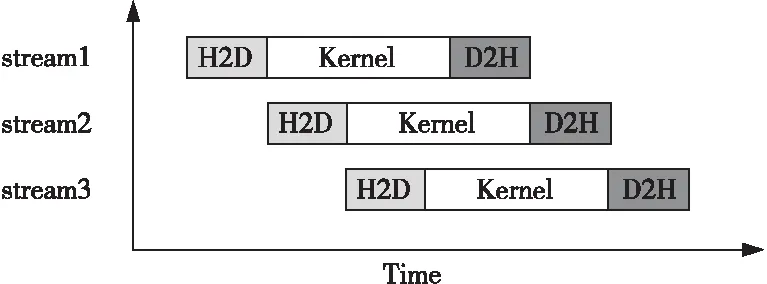
4.3 并行计算框架
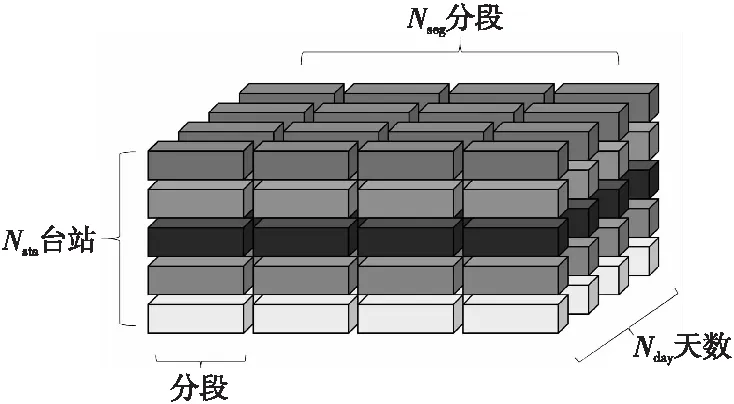
4.4 热点函数的CUDA实现
5 实验及结果分析
5.1 实验平台
5.2 实验方法及数据
5.3 实验结果



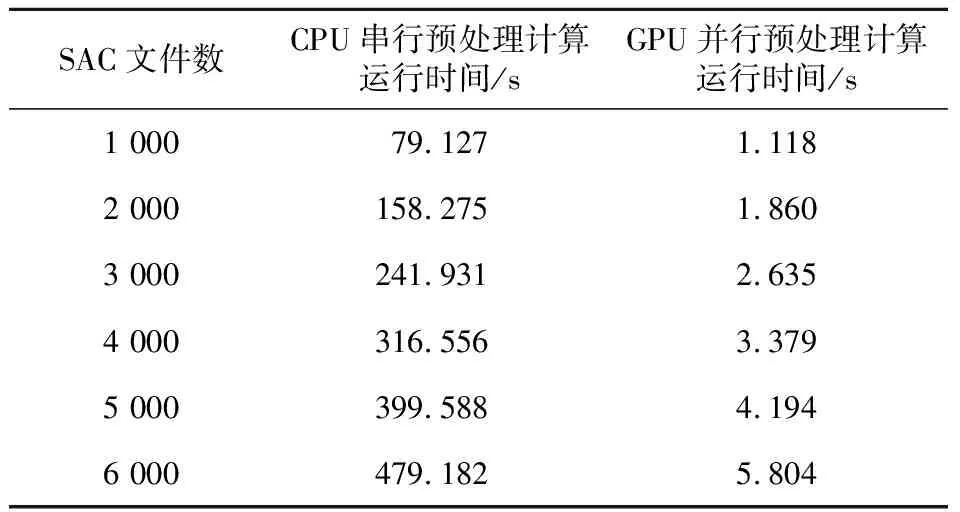

6 结束语
