基于Setwise排序的深度输入感知因子分解机*

刘 通,周宁宁

(南京邮电大学计算机学院,江苏 南京 210023)

1 引言

由于互联网的普及,信息过载成为人们生活中日益严重的问题。与搜索引擎一样,推荐系统[1]是缓解信息过载问题的有效解决方案,方便用户查看所需信息,增加服务提供商的流量和收入。推荐系统旨在从用户反馈中挖掘用户偏好。用户反馈包含显式反馈和隐式反馈。显式反馈指有明确评分标准的数值反馈,如豆瓣电影的五星制评分;隐式反馈没有明确的分值,如微博中的浏览记录。隐式反馈的特征是只有正反馈样本,传统协同过滤模型处理这类数据时会出现过拟合问题[2],因为观察到的正实例数量远小于未观察到的项目数量,这为构建推荐系统带来了新的挑战[3]。

传统的推荐算法大致可以分成3类:基于内容的推荐、协同过滤CF(Collaborative Filtering)[4]和混合推荐算法。这些传统的推荐算法重点考虑用户和项目之间的二元关系,大都可以转化为评分预测问题,根据用户对项目的评分进行排序后产生推荐列表。近几年,研究人员发现:如果仅根据用户对项目的评分产生的推荐结果并不能准确地反映用户的偏好[5]。

为了解决传统推荐算法中所存在的问题,研究人员将排序学习技术LTR(Learning To Rank)[6]融合进推荐算法之中。基于排序学习的推荐算法得到越来越多的关注,目前已经成为推荐系统领域的研究热点之一。Rendle等[7]提出了贝叶斯个性化排序BPR(Bayesian Personalized Ranking)模型,它基于成对式(Pairwise)排序方法,以正负项目对为基础,对隐式反馈中的偏好结构进行建模。Shi等[8]提出了ListRank-MF(Matrix Factorization),它将列表式(Listwise)排序方法与矩阵分解MF相结合用于协同过滤。然而,Pairwise排序方法存在独立性不一致问题,Listwise排序方法的损失函数较难设计且计算复杂度较高。Wang 等[9]提出了一种Setwise贝叶斯协同排序模型SetRank,以较弱的独立性假设和更宽的排序限制,在隐式反馈的top-N推荐中取得了最优的结果。

尽管针对隐式反馈的协同排序模型取得了很大进步,但当前基于排序的CF模型性能仍远不能令人满意。CF模型大都基于用户-项目的二维矩阵进行推荐,只考虑到协同信息,没有将用户和项目的内容信息融入模型中,这类模型容易存在冷启动问题。在现实世界的推荐系统中,冷启动问题通常被转化为基于内容的模型来解决。基于内容推荐的关键问题是如何有效地对内容信息和特征间交互关系进行建模。目前,由Rendle[10]提出的因子分解机FM(Factorization Machines)模型及其基于深度学习的变体,能够对用户、项目之间的交互以及内容信息进行有效的建模。

标准FM中为每个特征训练出的固定隐向量进行表示,但在实际应用中同一特征在不同数据场景下通常具有不同的预测能力。输入感知因子分解机IFM(Input-aware FM)[11],通过神经网络来学习出特有的样本感知因子,在不同数据场景下为特征分配不同的预测能力,以更好地反映其特定贡献。此外,虽然FM理论上可以建模特征间二阶以上的交互,但存在时间复杂度过大以及优化方法的数值稳定性差等问题,这阻碍了拟合特征间高阶交互的推广。随着神经网络和深度学习的兴起,研究人员考虑如何将因子分解机与神经网络相结合,提高模型最终性能。近年来,研究人员已提出DeepFM(Deep Factorization Machine)、NFM(Neural Factorization Machine)和xDeepFM(extreme Deep Factorization Machine)[12-14]等以不同形式融合因子分解机与神经网络的有效模型,并取得了优异的成绩。

为了获得可靠的个性化排序推荐结果,本文将实体的内容信息与隐式反馈相结合,构建了一种Setwise排序因子分解机SRFMs(Setwise Ranking Factorization Machines)模型,通过结合Setwise排序与因子分解机,提高了个性化排序的性能。为了避免标准FM中存在的固定特征表示及缺少高阶特征交互捕捉问题,本文将IFM中的影响估计计算网络FEN(Factor Estimating Network)和深度神经网络DNN(Deep Neural Network)相结合融入SRFMs,构建出SR-DIFM(Setwise Ranking Deep Input-aware Factorization Machine)模型。本文的主要工作总结如下:

(1)将实体的内容信息和隐式反馈相关联,提出一种基于Setwise排序的因子分解机模型——SRFMs,该模型不仅可以缓解冷启动问题以及避免Pairwise和Listwise协同排序中存在的弊端,并且内容信息的加入提高了个性化排序性能。

(2)为在不同数据场景下细化特征表示,同时学习低阶和高阶的特征交互,本文将FEN和DNN相结合后融入SRFMs模型,构建SR-DIFM模型,以进一步提高个性化排序的准确性。

(3)在2个真实数据集上进行了大量实验,以验证所提模型的有效性,结果表明,SRFMs模型和SR-DIFM模型可以提高个性化排序的性能。

2 相关工作

2.1 协同过滤模型

协同过滤的概念源于利用所有用户的协同行为来预测目标用户行为的思想。早期的模型通过使用基于内存的模型计算用户或项目的行为相似度来直接实现这一思想。这些模型可以在一定程度上预测用户的偏好,但由于用户复杂的偏好和简单的线性建模能力之间的冲突,其预测能力有限。与大型项目集合相比,每个用户的行为是有限的,因此CF面临的一个关键挑战是解决用户与项目交互行为的稀疏性,以实现准确的用户和项目的嵌入学习。

传统协同过滤算法大多关注预测用户对项目的绝对评分,而基于排序学习的协同过滤推荐算法[7-9,15,16]则从排序的角度看待推荐问题,更关注项目之间的排列顺序,被证明具有更好的推荐效果。排序学习推荐算法可以有效利用大多数信息系统中的隐式反馈进行推荐,例如点击、购买和查看历史等,并且排序学习方法还可以通过最小化排序损失来提供top-N推荐。

基于排序学习的推荐模型可以分为Pairwise模型和Listwise模型。Rendle等提出了BPR(Bayesian Personalized Ranking)模型,为个性化排序提供了一个通用的优化解决方案,成为广泛使用的Pairwise协同过滤模型。BPR中有2个基本假设:一是每个用户之间的偏好行为相互独立;二是同一用户对不同项目的偏序相互独立。然而Pairwise的独立性假设太过严格,在实际的偏好对构建过程中,往往会打破这种独立性,从而影响了Pairwise损失的优化结果[9]。一些后续研究试图通过考虑组信息来放松独立性假设,如分组贝叶斯个性化排序GBPR(Group Bayesian Personalized Ranking)模型[17]引入了更丰富的用户组信息,CoFiSet(Collaborative Filtering via learning pairwise preferences over item-Sets)[18]则定义了用户对项目组的偏好,但是独立性不一致问题仍然存在。

Listwise排序学习直接对项目的排序列表进行优化,主要有2种优化方式:一是通过定义损失函数反映预测列表和真实列表之间的差异,如ListRank-MF;二是直接优化排序学习中常用的评价指标,如NDCG(Normalized Discounted Cumulative Gain)、MRR(Mean Reciprocal Rank)[19]等。理论上,Listwise模型优于Pairwise模型,因为在问题建模时的信息损失更少。然而,Listwise模型的损失函数较难设计,且由于要对整个排序列表进行优化,模型的复杂度非常高。SetRank提供了一个新的研究视角,它使用排列概率来促使一个已观察的项目排在每个列表中多个未观察项目集合的前面,这样能够更加有效地模拟隐式反馈的特性。由于不需要对未观察项目集合内部进行排序,这放宽了列表法中的排列限制,并取得了最优的排名结果。

2.2 基于内容的模型

除了一般的用户-项目交互信息外,推荐问题通常伴随着辅助数据。辅助数据包括基于内容的信息和上下文感知的数据。具体来说,基于内容的信息与用户和项目相关,包括一般的用户和项目特征、文本内容(即项目标签、项目文字描述和用户对项目的评论)、多媒体描述、用户社交网络和知识图谱。上下文信息显示了用户做出项目决策时的环境,通常表示用户和项目以外的描述。

基于内容的模型[20]可以利用用户和项目的附加信息,这些附加信息通常是描述用户或项目的属性的内容,通过对这些内容建模来为用户推荐与其历史交互项目相似的项目。相对于基于协同过滤的推荐系统,基于内容的推荐系统能够缓解数据稀疏和冷启动问题。

FM是一种广泛使用的对特征交互关系进行建模的模型,能够较为有效地缓解数据稀疏和冷启动的问题。FM借鉴矩阵分解的思想,将每个参数用一个隐向量表示,用隐向量之间的点积表征组合特征的参数,可以用于分类、回归以及排序问题。尽管理论上FM能够对高阶特征交互进行建模,但是出于时间复杂度的考虑,FM模型一般只涵盖二阶交互;另外,标准 FM中所有特征之间相互平等,类别和层次信息无法得到体现,在建模过程中会受到噪声特征交互的影响。

随着深度学习技术在各领域的良好表现,近年来把深度学习技术和推荐系统相结合受到了广泛研究。神经网络因其能较好地学习抽象特征,大量研究提出利用深度神经网络来建模特征间更高阶的非线性关系。Cheng等[20]提出Wide&Deep模型,通过结合线性模型和深度神经网络来捕获特征的线性关系和非线性关系。He等[13]提出了NFM(Neural Factorization Machine)模型,该模型把FM模块和DNN(Deep Neural Networks)模块串行结合,其深度神经网络能够学习二阶特征的高阶非线性关系,使模型的表达能力更强。Guo等[12]提出了DeepFM模型,把FM模块和DNN模块并行结合,同时学习特征的低阶线性关系和高阶非线性关系。Yu等[11]提出了IFM模型,通过神经网络来学习出独特的样本感知因子,在不同数据实例场景下为同一特征分配不同级别的预测能力,以更好地反映其特定贡献。

3 本文模型

3.1 问题陈述

假设在一个隐式反馈数据集中有N个用户和M个项目。令Pi和Oi分别表示第i个用户的正反馈项目集合和未观察项目集合。本文的目标是建立一个排序模型,将用户偏好比较定义为每个正样本和一组未观察样本集合间的比较。对于每个用户,排序模型会从候选集中生成一个最佳排序列表,即用户感兴趣的项目会出现在列表的顶部。

3.2 模型构建

3.2.1 SRFMs模型

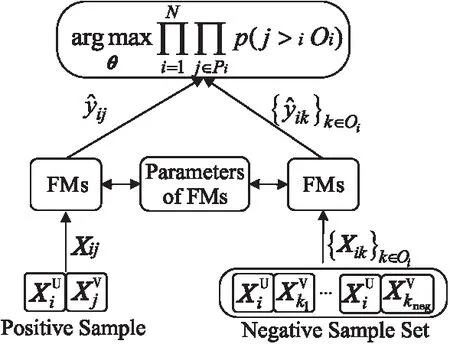
Figure 1 Structure of SRFMs

(1)

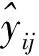
3.2.2 SR-DIFM模型

SRFMs可以认为是一个通用的框架,其中FMs可以纳入更复杂的技术。为解决标准FM中因每个特征训练的固定表示所带来的不利影响,以及标准FM受限于复杂度而无法进行高阶组合特征捕获的问题,本文提出将IFM中的FEN和DNN相结合后添加到SRFMs中,命名为SR-DIFM,以进一步提升排序学习精度。最终的模型结构如图2所示,图中变量符号含义在3.3节中有详细说明。SR-DIFM在SRFMs基础上融入了输入感知组件和深度神经网络组件,输入感知组件负责针对不同的输入,赋予不同特征以不同贡献的预测能力,达到细化特征表示的目的;调整后的特征嵌入分别输入到FM组件和深度神经网络组件中,以同时捕捉低阶特征交互和高阶特征交互,达到更佳的建模效果。

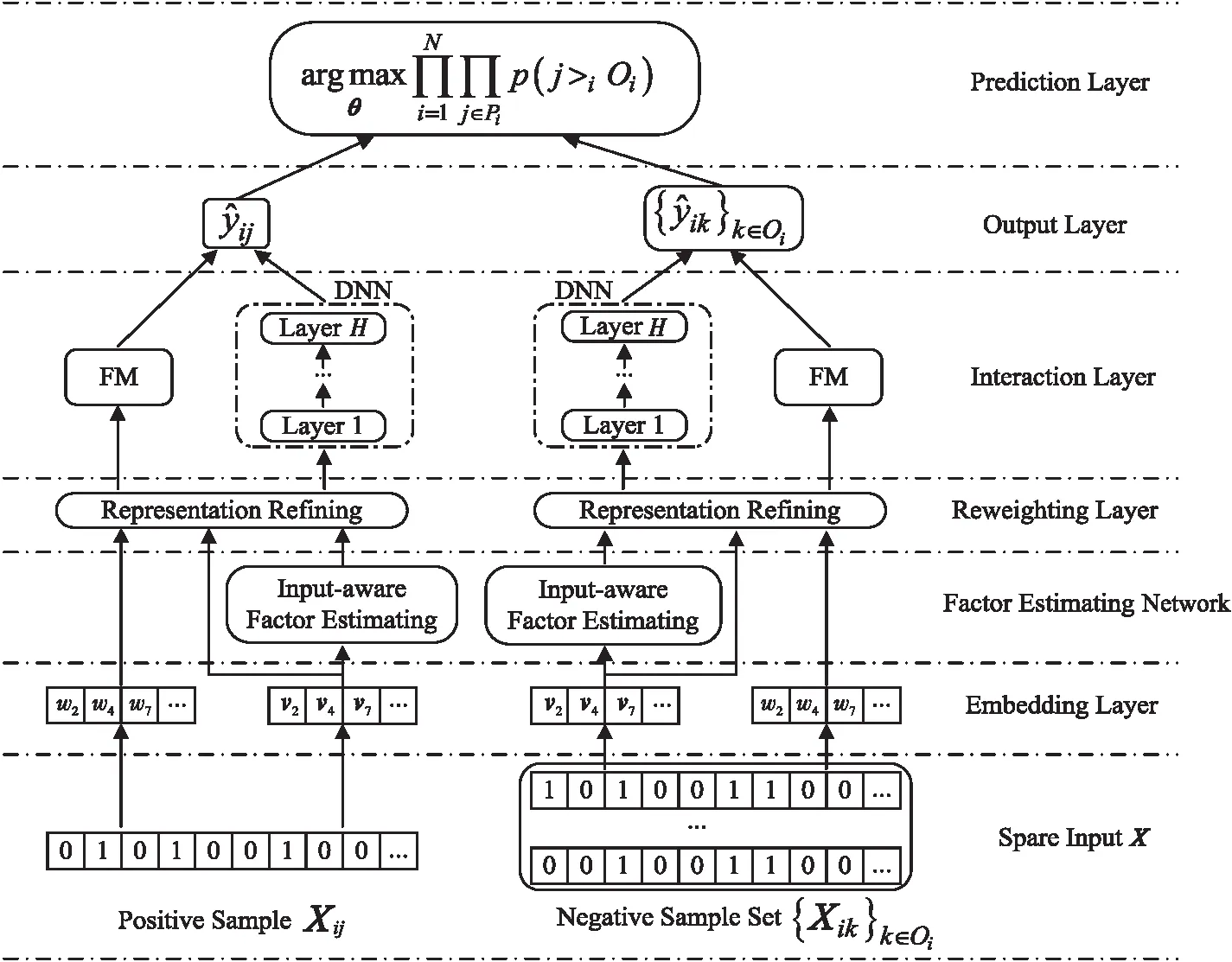
Figure 2 Structure of SR-DIFM

3.3 模型定义

(1)输入层。

SR-DIFM模型的输入分为正样本Xpositive和一组负样本构成的集合{Xnegative},其中负样本在隐式反馈数据中一般由采样器从未观察样本中抽取得到;输入向量包括了用户内容向量和项目内容向量,可以用式(2)表示:

X=[Xuser;Xitem]

(2)

其中,X∈R(m+n),Xuser∈Rm,Xitem∈Rn,m和n分别表示用户输入向量维度和项目输入向量维度。

(2)嵌入层(Embedding Layer)。

经过独热编码处理后的输入向量会变得非常稀疏,且维度很高,常用的处理方法是使用嵌入矩阵将它们映射到低维空间。具体而言,对于输入向量的每个特征采用式 (3)进行计算:

vl=Exl

(3)

其中,vl∈Rk表示输入向量的第l个特征的嵌入向量,k表示嵌入向量维度,E∈R(m+n)×k表示嵌入矩阵,xl是输入向量的第l个特征的独热编码。

(3)影响因子估计和特征细化层(Factor Estimating Network &Reweighting Layer)。

这2个部分参考了IFM中的组件,主要是通过输入的非零特征的嵌入向量,有针对性地计算出输入感知因子(Input-aware factor)mx,l,从而在后续影响特征权重wl和嵌入向量vl,得到针对不同输入细化后的特征权重wx,l和嵌入向量vx,l。

(4)特征交互层(Interaction Layer)。

交互层分为2个部分,即FM组件和DNN组件。FM组件是一个标准因子分解机,用于建模特征之间的线性和二阶交互。DNN组件是一个前馈神经网络,用于学习高阶特征交互。具体来说,将输入感知因子细化后的特征权重wx,l和嵌入向量vx,l分别输入到FM组件和DNN组件中,这2个组件共享特征嵌入向量,FM部分的计算如式(4)所示:

(4)

将细化后的嵌入向量作为DNN部分的输入,如式(5)所示:

a0=[vx,1,vx,2,…,vx,m+n]

(5)

其中,vx,l是第l个特征调整后的嵌入。

然后将a0输入神经网络,前向过程的计算如式(6)所示:

ah=σh(Whah-1+bh)

(6)

其中,σh(x)表示第h层神经网络的激活函数,h∈{1,…,H},H表示神经网络深度;ah,Wh,bh分别表示DNN部分第h层的输出向量、权重矩阵和偏差向量。

最终DNN部分的输出结果如式(7)所示:

yDNN=Whah

(7)

(5)输出层(Output Layer)。

(8)

3.4 训练

L=

(9)

4 实验和结果分析

4.1 数据集

为了验证本文提出的SRFMs和SR-DIFM模型的有效性,本节在2个真实的隐式反馈数据集(Frappe和Last.fm)上进行了大量的实验。

(1)Frappe:是一个上下文感知的应用程序发现工具公开的数据集,共包含96 203个不同上下文用户的程序使用日志。每个日志除了用户ID和应用程序ID之外,还包含了8个上下文变量,如天气、城市和国家等。

(2)Last.fm:用于音乐推荐,共包含同一天内1 000个用户的收听历史记录。每条记录包含4个上下文字段,用户上下文由用户ID和用户在过去90 min内收听的最后一首音乐的ID组成,项目上下文由音乐ID和艺术家ID组成。

2个数据集的具体信息如表1所示。

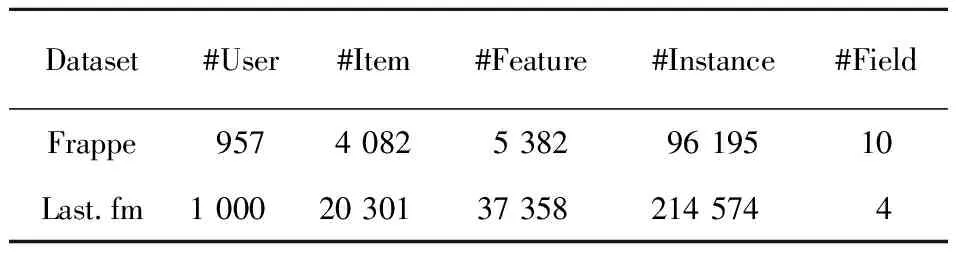
Table 1 Statistics information of datasets

4.2 对比模型

本文将SRFMs和SR-DIFM模型与以下模型进行比较:

(1)FM[10]:标准的因子分解机,在上下文感知预测方面表现出了很强的性能。

(2)DeepFM[12]:将神经网络和FM并行结合,弥补了FM对高阶特征交互建模的不足。

(3)IFM[11]:通过神经网络为不同实例中同一特征学习一个输入感知因子,从而细化标准FM中的特征表示,突出不同特征对于预测的贡献。

(4)PRFM(Pairwise Ranking Factorization Machine)[2]:使用BPR标准来优化模型参数,使用Pairwise排序的方式并利用FM结合内容信息来模拟用户对项目的偏好。

(5)SetRank[9]:一种最先进的优化的Listwise学习模型,其性能比大多数基于排序的模型的更好。该模型最大化Top-1排列概率,以保证每个用户更喜欢观察到的项目而不是未观察项目集合。

(6)NPRFM(Neural Pairwise Ranking Factorization Machine)[23]:在特征交互层之上叠加了一个与NFM功能相同的深度神经网络,弥补了PRFM在二阶特征交互建模方面的不足。

4.3 参数设置

为进行公平比较,本文参照对比模型的相应文献或实验结果来设置参数,然后仔细调整以达到最佳性能。对于所有测试模型,将嵌入维度都设置为64,批训练大小为2 048,优化器统一使用AdagradOptimizer,学习率(Learning Rate)为0.05,训练次数统一为500,其余参数按照相应文献中给出的参考值设定。对于本文提出的SRFMs和SR-DIFM模型,负样本集合大小参照SetRank的实验设置为30;神经网络部分,对于Frappe数据集使用3层网络,神经数量分别为128,64和64;对于Last.fm数据集使用2层网络,神经元数量分别为64和64;网络部分所涉及到的激活函数统一使用ReLU激活函数。FEN部分的设置同神经网络部分的。

4.4 评价指标

SR-DIFM的任务是为用户提供一个排序的项目列表,因此在进行性能对比时,本文采用在推荐算法中被广泛使用的评价指标:HR(Hit Rate)、NDCG和mAP(mean Average Precision)。本文对每种模型在Top-5、Top-10和Top-20的不同场景下进行实验,以充分展示该模型在实际应用中的效果,其中HR@5、NDCG@5和mAP@5分别代表前5项的HR、NDCG和mAP分数。

4.5 实验结果与分析

在2个真实的数据集上进行充分训练后,每个模型得出的最终结果如表2所示,其中,RI表示SR-DIFM模型相对于其他模型的平均相对提升。根据结果可以得出以下结论:

Table 2 Performance results of different models on two datasets

本文提出的SRFMs和SR-DIFM模型在2个真实数据集上取得了最好的成绩,优于所有的比较模型。首先,对于FM、DeepFM和IFM这类并非针对隐式反馈数据的模型来说,本文提出的SRFMs和SR-DIFM模型有非常明显的优势;相比于SetRank模型,本文的SRFMs在2个数据集上得到了21.96%和20.21%的平均相对提升,这表明上述基于Setwise排序并结合内容信息的思路是正确有效的;在后续改进的SR-DIFM模型中,进一步提升了原有的效果,达到了29.33%和26.70%的平均相对提升,这说明细化特征表示及高阶特征交互的加入有助于提升推荐精度;相比于最先进的成对学习模型NPRFM,本文的SR-DIFM模型也取得了36.35%和63.70%的平均相对提升,这也验证了Setwise比Pairwise能更好地贴合推荐系统中隐式反馈的特征。

Figure 3 Performance results of SR-DIFM model at different learning rates

Figure 4 Performance results of SR-DIFM model with different sizes of negative samples sets

对于Frappe数据集,当negNum达到30后,HR基本保持稳定水平,NDCG和mAP保持上升趋势,分析认为HR强调预测的绝对准确性,而NDCG和mAP更强调预测结果的相对顺序性,随着负样本数量的增加,模型可以比较更多的正负样本集合,这将更有利于对隐式反馈的利用,也更有利于NDCG和mAP这类与位置相关的指标,但对于HR的影响较小。在Last.fm数据集上的2个指标的趋势大致和Frappe上的类似,不同的是Last.fm上2个指标都有不同程度的波动。本文认为是由于Last.fm的数据量大于Frappe的数据量,数据集中的未观察项目规模也远远大于观察项目规模,数据偏斜问题更严重,持续增加负样本数量,可能会导致采样的观察样本和未观察样本集合不一致问题,影响模型的性能,这也激发后期开发更合理有效的采样方法。综合来看,本文认为负样本集合不超过50比较合理。

4.6 消融实验

本节对SR-DIFM模型进行消融实验,对输入感知模块和高阶特征交互模块进行遮盖性对比,以更好地了解每个模块的具体贡献。本节将SRFMs作为基准模型,No-FEN表示从SR-DIFM中删去输入感知模块,No-DNN表示从SR-DIFM中删去高阶特征交互模块,实验结果如表3所示。从表3可以看出,FEN和DNN对于SR-DIFM的性能都是必要的,当删除任何组件时,都会导致性能的明显下降。另外,在SR-DIFM中,FEN和DNN似乎一样重要,二者都会带来明显的性能提升。以上实验结果说明样本输入感知和高阶特征交互的捕捉都是必不可缺的。

Table 3 Performance results of different components in SR-DIFM model

4.7 关于负采样的讨论

前文实验中,出于效率的考虑选择了简单的随机负采样方法。目前负采样方法还包括了基于流行度的负采样和基于模型的负采样方法等。随机负采样逻辑简单,在效率上有很大优势,同时也避免在采样过程中引入新的偏差,因此被广泛使用。而在实际场景中,首先并非所有未观察项目都是负样本,因此引入了伪负例问题[24],这会对模型训练造成影响;其次,对于每个正样本来说,不同负样本带来的影响并不相同,一种观点认为,强负例采样可以提高采样质量,从而提升模型的训练结果[25]。目前基于流行度或模型的负采样方法,虽然有助于加快模型的训练收敛速度或者提升最终效果,但也伴随着引入新的偏差的风险,或带来较大的时间开销,最终影响模型的训练。综合来看,随机负采样仍是比较理想的选择。

5 结束语

传统个性化排序使用的Pairwise和Listwise模型都存在一些不足,影响了最终的优化结果。SetRank中使用的Setwise排序方法因具有较弱的独立性假设且更贴合隐式反馈的特点,在top-N推荐中取得了优异成绩。本文构建了一个新的模型——SRFMs,将隐式反馈与内容信息结合起来,使用Setwise排序方法完成个性化排序任务,解决了SetRank精度不佳和冷启动问题。受IFM的启发,对SRFMs进行扩展,融入影响估计计算网络和深度神经网络以规避标准FM中存在的问题,扩展后的SR-DIFM模型根据不同的实例来重新确定特征的表示并能够同时学习低阶和高阶特征交互。大量实验结果表明,在2个真实数据集上,SRFMs和SR-DIFM模型的3个指标值(HR、NDCG和mAP)均优于当前的先进模型的。

本文的工作还有改进的空间。在负采样方法上,选择了简单的随机负采样,后期计划设计更高效合理的负采样方法,缓解某些场景下负样本集合过大导致的性能波动问题,并提升模型的训练效率,加速模型收敛。另外,隐式反馈虽然缓解了数据稀疏问题,但隐式反馈中的大量噪声可能会产生严重的负面影响,未来计划加入去噪训练,识别和剪枝噪声交互,提升推荐训练的有效性。