结合对比监督和排序树的轨迹数据差分隐私保护方案*

王 辉,陈 宇,申自浩,刘沛骞

(1.河南理工大学软件学院,河南 焦作 454000;2.河南理工大学计算机科学与技术学院,河南 焦作 454000)

1 引言

随着定位设备的增多,移动定位设备产生轨迹数据的速度以指数级增长。移动设备硬件的快速发展使得利用GPS获取用户的信息变得异常容易,只要用户授权,用户的位置信息就可被运营商服务器随时随地地获取[1-3]。轨迹数据是一种规模大、变化快、用户普遍关注的位置信息,主要来源于车辆网络、移动设备、社交网络等[4]。现在轨迹数据的许多应用方便了人们的日常生活,因此轨迹数据服务被称为一种新的移动计算服务[5]。然而,大量用户的轨迹数据被收集和存储,且对轨迹数据进行分析处理,对用户的隐私安全来说是一种不可见的隐患。根据用户的轨迹可以推断出用户的敏感信息,如个人爱好、家庭住址等。当从轨迹中提取出具有高度价值的信息点时,用户的数据隐私已经不具有安全性。若不做好轨迹隐私保护措施就肆意发布给研究人员进行分析挖掘,用户的私密信息甚至人身安全无疑将受到严重的威胁[6],所以对于轨迹隐私的保护一直都是非常必要的研究。

2006年由微软研究院的科学家Dwork提出的差分隐私保护技术是隐私保护研究中常用的技术。作为一种可严格证明的隐私保护模型,差分隐私保护技术严格定义了隐私保护的强度,任意一条记录的添加或删除都不会影响最终的查询结果。同时,该技术定义了极为严格的攻击模型,不关心攻击者的背景知识,即使攻击者掌握了除原数据外的任何辅助信息,差分隐私仍能将原数据的隐私泄漏风险控制在一个可接受的范围[7]。隐私预算分配是决定数据隐私是否安全的一个重要因素。吴万青等人[8]提出一种等差隐私预算分配算法,在树形存储结构不同的高度为数据分配不同大小的隐私预算,能有效保证数据可用性,但不适用于多种树形结构,无法保证隐私预算在其他树形结构中的合理分配。傅继彬等人[9]提出了一种高效的分层细化方法MAXGDDP(MAXimum Geometric Distribution Differential Privacy),对原始分类数据进行分层细化,在同一层次的概念细化中提出了最大值属性索引算法,在不同层次之间利用类几何分配机制来更加合理地分配隐私预算。Yuan等人[10]提出了一种平均隐私预算分配方法,使用约束一致性规定隐私的分配,在不同层高分配相同的预算对抗具有信息背景知识的攻击,但隐私预算分配不够合理,不能有效提高利用率。徐川等人[4]提出了一种基于差分隐私的个性化位置隐私保护方案,在保护用户隐私的前提下,满足用户个性化隐私需求。该方案通过定义归一化的决策矩阵,描述导航推荐路线的效率和隐私效果;引入多属性理论,建立效用模型,将用户的隐私偏好整合到该模型中,为用户选择效益最佳的驾驶路线;根据用户的隐私偏好需求,以距离占比为衡量指标,为用户分配合适的隐私预算。Zhao等人[11]提出了一种基于前缀树的差分隐私轨迹数据保护方法。该方法首先提出了轨迹段前缀树的概念,然后基于MDL(Minimum Description Length)原理提出了PMDL(Point Minimum Description Length)方法,以降低数据处理的时间和空间复杂度;然后,利用Dijkstra算法寻找最佳轨迹分割,利用差分隐私方法对轨迹段进行保护;最后,采用马尔可夫链限制噪声量,从而保证用户的隐私信息和数据可用性。

计算轨迹之间相似度的方法在近些年不断更迭。Yu等人[12]提出了一种增强的轨迹模型,并提出了一种基于多特征轨迹相似度度量的轨迹聚类算法,可以最大化同一聚类中的轨迹相似度,更好地服务于交通监控、道路拥堵等应用。Yao等人[13]提出 NeuTraj(Neural Trajectory)来加速轨迹相似度计算。NeuTraj可以适应任何现有的轨迹测量,并且可以快速计算给定轨迹对在线性时间内的相似性。此外,NeuTraj具有弹性,可以与所有基于空间的轨迹索引方法协作,以缩小搜索空间。Liang等人[14]提出了一种无监督的学习方法。该方法通过卷积自编译器CAE(Convolutional Auto-Encoder)自动提取低维特征,在保持时空特性的同时,首先将原始船只轨迹重新映射为二维矩阵生成信息丰富的轨迹图像,然后基于采集到的大量船舶轨迹,CAE无监督地学习信息轨迹图像的低维表示,轨迹相似度最终等价于低维特征之间的相似度,这些特征与原始船只轨迹具有很强的相关性。Li等人[15]首次提出了把深度学习模型用于轨迹相似度度量的方法,该方法对低质量数据具有鲁棒性,能够支持准确和高效的轨迹相似度计算和搜索。Liu等人[16]提出了考虑轨迹差异的深度学习模型,新的对比模型区分了轨迹之间的轨迹级和点级差异来学习轨迹表示,有效提高轨迹相似度度量的科学性。

上述方法在轨迹数据的存储方面还存在存储结构检索效率不高的问题;当轨迹数据量比较大时,会出现无法高效计算与比对的问题。为此,本文提出一种结合对比监督模型和排序树的轨迹数据差分隐私保护方案SDTS(Supervised Differential Trajectory Sort),用于轨迹数据的存储与发布;通过监督学习模型来保障轨迹数据的充足有效;利用损失函数计算轨迹之间的轨迹相似度,根据轨迹之间的相似性将轨迹存储到基于二叉排序树的排序树中对应的节点中;利用差分隐私技术对其节点存储的敏感数据添加噪声。本文工作主要包括以下3个方面:

(1)为了提高轨迹查询效率,提出一种基于二叉排序树的存储树形结构,以提高查询速率。通过比较轨迹之间的相似性计算结果,把用户轨迹信息存储到所对应的节点。

(2)为保证轨迹相似度计算的精确度,将对比监督学习模型加入到轨迹存储的方案中,有效保障结果的科学性。

(3)采用等比隐私预算分配的方式为节点中的敏感数据添加噪声,通过阈值判断隐私预算分配的合理性,保障数据的可用性。

2 预备知识

定义1(轨迹) 轨迹是移动用户在时空里按照顺序,通过一系列连续位置点组成的集合T=P1→P2→…→Pn,其中n为轨迹中位置点的个数,Pi是二维空间点坐标(xi,yi)。

定义2(轨迹数据集) 轨迹数据集由多个轨迹数据组成D={T1,T2,T3,…,Tm}。其中m代表轨迹数据集中的轨迹总数,Ti表示数据库中第i个轨迹数据对应的轨迹信息。

定义3(原轨迹) 预先对轨迹进行分类处理,规定出现重要轨迹点最多的轨迹是原轨迹。

定义4(全局敏感度) 对于2个数据集D1和D2,给出任意的查询函数f:D→Rd,则全局敏感度如式(1)所示:

Δf=maxD1,D2‖f(D1)-f(D2)‖1

(1)

其中,‖·‖1是一阶范数距离,即曼哈顿距离。

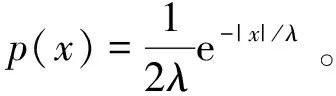
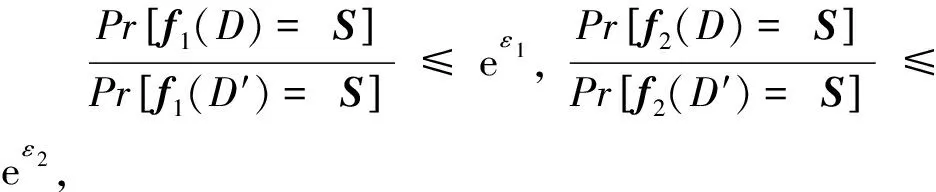
(2)

其中,Pr[f(D)=S]表示数据集D通过函数f输出的值等于S的概率,S表示函数f输出的所有可能。

定义7(并行组合性[18]) 假设Di(1≤i≤n)是原始数据集D中彼此不相交的子集,对每个子集Di作用一个差分隐私函数fi,其隐私预算为εi,函数组合F(f1(D1),f2(D2),…,fn(Dn))提供(maxεi)-差分隐私保护。则称函数fi在D上的并行组合满足(maxεi)-差分隐私。

定义8(信息推理攻击模型[19]) 攻击者利用出行目的、出行方式等背景知识,从移动用户的非轨迹位置信息中,直接或间接地推断出用户的出行轨迹、家庭地址等敏感信息的模型。

3 轨迹相似度计算

3.1 预训练轨迹编码

编码器-解码器模型是当前研究中常用的轨迹表示模型,但是该模型在重建时会忽略轨迹之间的点级差异,造成排序任务的准确度降低。加入一种对比模型,通过区分轨迹之间轨迹级和点级差异来训练学习轨迹表示,并保证非均匀采样率和数据噪声的鲁棒性。在训练轨迹数据不足的情况下,使用一种自监督方法来增加训练轨迹对[16]。

对比模型如图1所示。通过和一个对比目标比较来区分轨迹级和点级的差异,以学习轨迹表示。

Figure 1 Contrast model

给定1条原轨迹和2条候选轨迹,通过识别其差异来选择相似的轨迹。为了保证模型对非均匀采样率和数据噪声的鲁棒性,将点级差异限制在一个较小的范围内。

本文模型分为2个部分:编码器和对比损失函数。编码器使一条轨迹T变成一个表示向量f(T),对比损失函数通过比较原轨迹和候选轨迹的相似性来训练编码器,然后选择相似的轨迹。

编码器总体结构如图2所示。嵌入层的作用是将每个定位点转换为相对固定的输入嵌入。具体来说,对于给定的标记,其输入嵌入是通过将相应的标记嵌入和位置编码相加来构造的。标记嵌入是一个可学习的向量,位置编码包含了标记在轨迹中的位置信息。

Figure 2 Encoder

为了获得固定长度的轨迹表示,本文向上下文向量添加一个池化层。本文采用了2种池化策略:(1)CLS(CLaSsification):利用CLS的上下文令牌;(2)MEAN:使用所有上下文令牌的均值。默认使用的策略是MEAN。

为了捕获轨迹的上下文信息,采用掩模轨迹模型对编码器进行预训练。该模型随机地屏蔽了轨迹上的一些定位点,其目标是根据其上下文对掩蔽点进行预测。本文使用了一批包含50%原始轨迹和50%噪声轨迹的预训练数据,在每个轨迹中随机屏蔽15%的标记。

3.2 自我监督数据增加

本文使用了一种自监督的方法来生成包含轨迹级和点级特征的轨迹对。

首先,使用下采样机制来生成包含轨迹级差异的轨迹对。给定原轨迹T,通过降低一些定位点的比率生成正轨迹T2。然后随机选择另一个轨迹Q作为它的负轨迹。正轨迹与原轨迹具有相同的轨迹级特征。经过训练后选择正轨迹时,可以识别2个候选轨迹之间的轨迹级差异,并获得轨迹级特征。接下来,使用下采样机制来增加具有点级差异的轨迹对。正轨迹T1和负轨迹T2通过丢弃相同的点生成,正轨迹相比负轨迹具有更低的丢弃率。这2种增量轨迹具有相同的轨迹级特征,但负轨迹的采样点较少,噪声较大。自监督方法通过区分差异来学习T1和T2之间的点级特征。

3.3 对比损失函数

设gap1和gap2分别表示轨迹级差和点级差,其计算方法分别如式(3)和式(4)所示:

gap1=sim(T,T2)-sim(T,Q)

(3)

gap2=sim(T,T1)-sim(T,T2)

(4)

sim(Ti,Tj)=cos(f(Ti),f(Tj))=

(5)

为了更好地区分轨迹级和点级的差异,应当最大化gap1和gap2。使用一个损耗函数,并设定gap1和gap2的下限为ε1和ε2。此外,为了提高模型对非均匀采样率和数据噪声的鲁棒性,gap2不能太大。限制gap2的最大值为ε3,如式(6)所示:

L=max(ε1-gap1,0)+max(ε2-gap2,0)+

max(-ε3+gap2,0)

(6)

gap1和gap2对模型性能有至关重要的作用。一个较小的gap1会导致监督学习模型无法获取轨迹级特征,一个较大的gap1会增加模型训练的难度。一个较小的gap2能限制数据噪声的影响,因此可以高效率地表示带有鲁棒性任务的数据噪声。然而,在处理排序任务过程中,一个较小的gap2又会增加轨迹排列错误的概率。

4 轨迹数据保护

4.1 轨迹排序树

二叉排序树在中序遍历中可以得到一个有序序列。构造二叉排序树的过程即是对无序序列进行排序的过程。在轨迹存储中,单一的排序树节点存储没有现实意义,轨迹是对空间位置点采样得来的序列,既具有空间特征,又具有时间特征。结合轨迹的时空性和二叉排序树的特点,本文提出了一种基于二叉排序树的轨迹排序树结构。该结构既保证了轨迹的时空完整性,又可以对轨迹进行快速查询。为了保证轨迹的时空特征,轨迹点序列存储在具有时空特征的轨迹相似树节点中。

下面给出构建轨迹排序树的步骤:

步骤1数据初始化。结合实际情况,将相同移动用户的轨迹数据分在同一组,并计算具有相同轨迹的移动用户数据,一个节点的数据结构为{N(p),T(p),C(p),S(p)},其中p表示轨迹,N(p)为轨迹相似度,T(p)为轨迹点序列,C(p)为相应轨迹点序列上的所有移动用户数量,S(p)为敏感信息。

步骤2节点选取。新的轨迹点序列插入时,从根节点开始向下遍历,比较相似度大小。若轨迹相似度大于根节点相似度,插入根节点的右节点中;若轨迹相似度小于根节点相似度,则插入根节点的左节点中;若轨迹相似度相同,轨迹点序列和相应轨迹点序列用户数量和其他信息并入根节点。

步骤3更新父节点。在排序树中,插入新的轨迹点序列数据时,需要更新父节点的索引记录。根据轨迹相似度数值在排序树中找到节点的添加位置,并更新父节点的用户计数值。

步骤4加噪处理。经过前面步骤的处理后,需要保护节点中存储的数据信息,用于抵抗攻击者的攻击。本文采用差分隐私技术对节点信息中的计数进行保护,对隐私预算分配采用等比分配方式。

图3给出了一个轨迹排序树的示例。

Figure 3 Sorting tree

排序树的节点存储轨迹的相似度值、轨迹点序列、所有移动用户数量、背景知识和上下文的敏感信息。以根节点T1为例,60表示与目标轨迹的相似度值,3表示移动用户的数量,S1表示背景知识和上下文敏感信息。

假设添加的轨迹点序列T6的相似度为70,在排序树中插入节点后如图4所示。

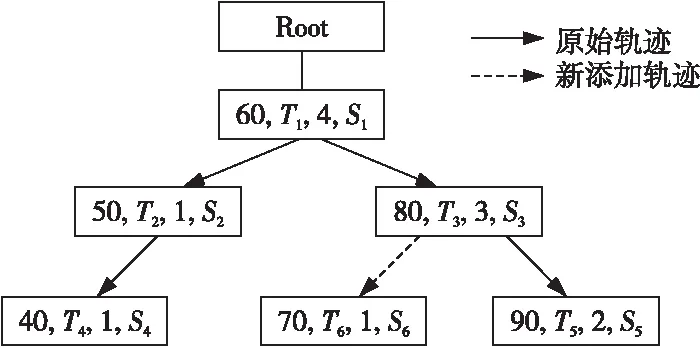
Figure 4 Sorting tree after adding the new node

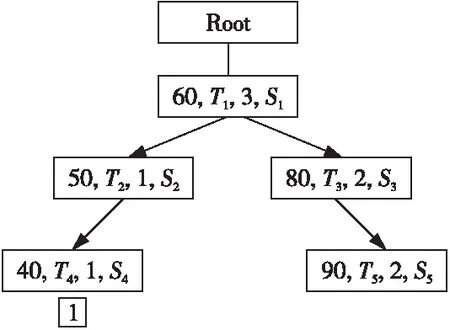
添加新轨迹节点,首先要计算轨迹相似度;然后,根据计算的相似度结果添加到相对应的节点位置。从根节点依次往下比较相似度值。从图4可以看出,新节点添加到了T3的左子树上。同理,假设添加的轨迹点序列T7的相似度为30,新节点会添加在T4的左子树上。但是,此时排序树是不平衡二叉树,查询效率不高。为了提升查询效率,对排序树进行了优化处理,如图5所示。

Figure 5 Balanced sorting tree

通过右旋转使排序树变成一棵平衡二叉树,解决了不平衡树结构造成的查询效率低的问题。同理,右子树造成的排序树不平衡问题也可以采用相对应的旋转方法解决。

4.2 差分隐私保护方案

改进后的排序树保存了移动用户的空间位置信息。一系列连续的位置点构成一条轨迹序列,位置点具有顺序特征。可见,轨迹具有时空性,即空间位置和时间特征。大多数轨迹隐私保护不关注轨迹时间特征。但是,在轨迹的相似性计算比较中,轨迹的时间特性具有提高轨迹相似度计算准确性的作用。本文基于二叉排序树提出了一种改进的轨迹排序树,在保证轨迹时空特征的同时,能够有效地提高轨迹的检索效率,降低复杂度。

通过二叉树规则完成轨迹树的排序,使其中序遍历是一组从小到大的顺序排列的轨迹相似度值,最底层的节点中的轨迹分别代表最相异原轨迹和最相似原轨迹的轨迹,2种计算结果具有同等重要性。

对于给定的轨迹排序树,规定以下限制约束:

(1)对于排序树中的任意一个节点,如果该节点不是根节点或父节点,那么该节点上的移动用户数量需要不大于父节点或根节点的。

(2)对于排序树中的任意一个非叶子节点,其节点上的移动用户数量是其所有子节点的移动用户数量之和。

本文使用等比数列隐私预算分配算法。对于给定的隐私预算和排序树结构高度,根据不同比值q的计算,每层的隐私预算分配都不同,如式(7)所示:

(7)

由式(7)可知,当q=1时,排序树每层结构分配的隐私预算相同;当q>1时,从根节点到叶子节点每层结构分配的隐私预算为以q为单位逐级递增。根据隐私保护度的不同需求来调整q值,选择合适的隐私预算分配方案。使用不同的比值q,隐私预算会根据q值的不同而变化,找到一个合理规范的最优比值,既可以有效合理地分配预算,又能够在保证数据可用性的同时保证数据安全性。

通过在轨迹排序树上的位置数据等信息中添加拉普拉斯噪声,能够有效对抗攻击者对轨迹的信息推理攻击,从而保护用户隐私。本文采用等比数列隐私预算分配算法,并对每一层设置相应的阈值Qi来限制噪声量的添加。本文定义第i层阈值为a×i-1+b,a>0,b>0,a和b为阈值参数。若加噪后节点计数值超过阈值,则必须重新选择噪声量,直到可以通过,具体如算法1所示。

算法1等比数列隐私预算分配算法GPPA(Geometric Progression Privacy Assignment)

输入：轨迹数据集D,总隐私预算ε和树高度h,常数q。

输出：噪声保护数据集D′。

步骤1初始化ε,h和q;

步骤2创建高度为h的排序树和根节点;

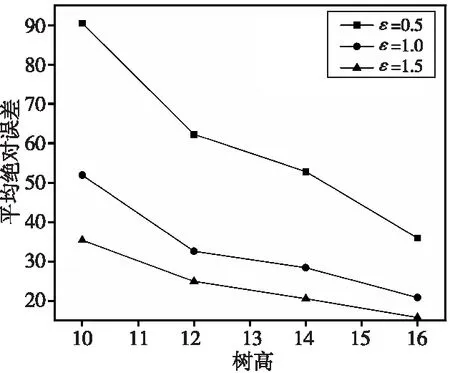
步骤3fori

步骤4if(q=1)then

步骤5εi=ε/(h+1);

步骤6else

步骤7εi=εqh-i(1-q)/(1-qh+1);

步骤8endif

步骤9Qi=a×i-1+b;

步骤10for每一个vi节点的孩子节点vi+1do

步骤11vi+1·count=vi+1·count+Lap(1/εi+1);

步骤12ifvi+1·count≤Qithen

步骤13节点vi+1存入排序树中;

步骤14sum=sum+vi+1·count;

步骤15ifsum>vi·countthen

步骤16break;

步骤17endif

步骤18endif

步骤19endfor

步骤20endfor

步骤21returnD′

4.3 查询处理

轨迹排序树建立轨迹序列的索引结构,帮助实现轨迹数据的查询和存储。查询过程中通过轨迹相似度查询节点,查询具体步骤如下所示:

步骤1从上到下遍历轨迹排序树,顺序访问所有节点;

步骤2计算查询轨迹和目标轨迹之间的轨迹相似度;

步骤3根据计算结果查询排序树中相对应的节点;

步骤4返回查询结果和节点中移动用户数量。

下面简单说明轨迹排序树的查询处理过程。假设给定查询轨迹T4,轨迹之间的轨迹相似度为40,查询结果为查询节点的移动用户数量。

如图6所示,通过比较轨迹排序树中相似度值判断节点的位置。根节点T1的相似度为60,大于T4的相似度,根据二叉排序树的性质继续查询左子树。左子树上T2的相似度为50,大于查询节点相似度,继续查询左子树。查询到左子树的相似度等于40,说明此节点为所要查找的节点。最后,将查询到的节点中的移动用户的数量返回。

Figure 6 Query processing

5 实验及结果分析

本文主要从数据可用性、查询效率及隐私保护程度3个方面来评估方案的有效性。Yuan等人[10]提出了一种平均级数差分隐私预算分配方案DPTS(Differential Privacy Trajectory Similarity);Zhao等人[11]提出了一种基于前缀树的差分隐私轨迹数据保护方案NTPT(Novel Trajectory Privacy Tree)。本节将本文方案SDTS与上述2种方案进行比较。

实验使用的数据来自ECML/PKDD 15的出租车轨迹数据[20],测试数据随机选择10 000条轨迹构造轨迹数据集。本文使用的模型在PyTorch中实现,通过编码器对轨迹进行训练,编码器和解码器固定为3层,模型的隐藏尺寸大小默认为256。实验环境为Windows11 64位操作系统,16 GB内存,Intel®CoreTMi5-12500H @3.10 GHz。

5.1 数据可用性分析

本节对本文提出的隐私保护方案SDTS进行数据可用性分析。数据可用性和隐私保护程度成反比,轨迹数据中加入的噪声越少,真实数据的干扰越小,发布的数据可用性就越好。所以,选取一个合理的隐私预算分配机制可以有效增强数据的可用性。本文采用平均绝对误差来衡量数据可用性。平均绝对误差计算公式如式(8)所示:

(8)

其中,m代表数据库集包含的总轨迹数,Di表示原始数据集,D′i表示隐私保护后的数据集,|Q(Di)-Q(D′i)|表示查询计数值产生的绝对误差。

在不同的隐私预算下,根据不同的轨迹总数之间的对比检测数据可用性。本文将实验分为4组,轨迹数分别为50,100,150,200。每组实验20次,取平均值作为最终实验结果。实验结果如图7所示。

Figure 7 Mean absolute errors under different number of trajectories

在相同的轨迹总数下,平均绝对误差随着隐私预算的增加而减小。而随着轨迹总数的增加,平均绝对误差也随之增加。因为轨迹数增加,排序树高度会随之增加,导致加入树中节点轨迹的噪声增加,进而造成平均绝对误差增大。实验结果显示,与其他方案相比,本文方案SDTS更优,平均绝对误差最小,相对其他方案更加有效。

5.2 查询效率分析

本节对本文提出的隐私保护方案SDTS进行查询效率分析。查询效率和查询次数成正比。查询的次数越多,说明查询效率越低;反之,查询次数越少,说明查询效率越高,所使用到的方案查询效果越好。查询效率计算公式如式(9)所示:

(9)

其中,m代表总轨迹数,N(Di)代表查询节点的次数。

通过比较方案查询次数分析不同方案之间的查询效率。本组实验考虑了50,100,150,200的轨迹总数。每组实验20次,取平均值作为实验结果。

如图8所示。总轨迹数增加会导致树增高,查询次数随之增多。通过实验不同的轨迹总数发现,在相同的轨迹总数下,本文提出的隐私保护方案SDTS查询次数都低于其他方案的,查询效率更高,随着实验轨迹总数的不断增加,两者的查询效率相差更加明显。因为随着轨迹数量的增加,树形存储结构高度也随之增加,导致查询的次数以倍数增加。其他2种方案每次查询都需要对根节点下的所有节点进行遍历查询,导致查询效率较低。而本文使用的排序树方案不需要全部遍历,只需对比相似度值,进而其查询效率大大优于其他方案的。

Figure 8 Query ratios under different trajectories

通过实验结果表明,本文方案SDTS查询效率相比其他方案有明显优势。

此外,考虑到大数据对实验结果的影响,本文在本组实验基础上加入大数据量轨迹数据进行实验对比。当轨迹数量增加到1 000条以上时,实验结果对比出现了数倍的差异。NTPT和DPTS的查询比值分别为0.85和1.08,本文排序树查询比值为0.025。这表明,使用本文树形结构的查询比值是其他2种对比方案的数十倍以上,这明显地表明了本文提出的SDTS方案在大数据量轨迹数据上的优势。

5.3 隐私保护分析

数据隐私保护性和数据可用性都是比较重要的属性。当数据加入的噪声相对较多,隐私保护性增强,数据可用性就会减弱;反之,加入的噪声较少,隐私保护程度就不够强,但数据可用性会更优。本节测试在不同的预算分配算法下,数据的隐私保护程度随着树形结构的树高而发生的变化。本文分析了在不同的树高下不同的隐私预算算法对平均绝对误差的影响,如图9所示。

Figure 9 Mean absolute errors under different privacy budgets

本文方案SDTS的平均绝对误差随着隐私预算算法的增加而减少。原因在于:隐私预算越大,添加的噪声越少,数据可用性越好,隐私保护程度越低。

6 结束语

进入电子信息时代后,电子设备获取用户包括敏感信息在内的各种位置信息后,通过分析对比这些数据信息,可以为用户提高服务质量。但是,在数据发布过程中会有数据泄露的现象发生,因此在数据发布过程中如何防止数据泄露是一个重要的研究问题。

本文提出了一种用于轨迹隐私保护的排序树方案SDTS,该方案通过排序树结构存储轨迹序列,避免了破环轨迹的时空性问题。在排序树节点存储轨迹之间的相似度和其他敏感信息,使用差分隐私对其数值做加噪处理,以保障发布的数据信息不会轻易泄露。实验结果表明,在数据可用性和查询效率上,本文方案SDTS优于其他方案,能有效保护轨迹隐私,且同时能保证数据的可用性。

轨迹隐私保护是未来一段时间里一项具有重大意义的研究课题。大数据时代里各种设备产生大量的位置信息,操作不当会导致大量的用户轨迹数据信息泄露,这对轨迹隐私保护是一项重大挑战。在未来的研究中将主要关注以下几点:(1)在轨迹相似度计算时,如何有效提高准确性,保证数值的科学性;(2)进一步优化差分隐私预算分配算法,提高数据可用性。