含五次非线性刚度超结构中弹性波的传播特性研究

蒋戴宇，张 晨，章 宁，刘 帽

（江苏大学 土木工程与力学学院，江苏 镇江 212013）

0 引言

在研究弹性波传播特性之前，我们需要知道弹性波的固有特性，首先便是弹性波带隙。目前关于弹性波带隙的形成机理主要有两种，一种是布拉格散射（Bragg Scattering）机理，另一种是局域共振（Locally Resonance）机理。关于布拉格散射，早在2000 年，刘正猷[1]用硅橡胶包围的三维铅球来组成新的结构，并发现了发现新的带隙所对应的波长远远大于晶格常数。而关于弹性波带隙的理论解决方法，在2009 年由温淑花[2]等学者提供了声子晶体及其应用说明。

Ozkaya 和Yilmaz[3]研究了涡流阻尼对局域共振声子晶体带隙结构的影响。Lei[4]提出了局域共振声子晶体的结构可以调整带隙共振声子晶体，研究了原胞接触状态对局域共振带隙的影响，发现通过设计复合提出了复合局域。

其次我们需要了解的便是弹性波的局部共振机理。而关于局部共振机理，Wang[5]提出了具有低频局域共振带隙特性的五模超材料，可以做到利用较小几何结构对长波长进行管控。Vakakis 等[6]考虑外力和地弹簧的非线性链，识别出了传播和衰减区域基于长波长连续性假设和多尺度摄动方法研究。

本文在前人研究三次非线性传播规律的基础上，利用多尺度法研究其五次传播特性位移解。利用多尺度法展开方程并得到一次近似解与非线性的修正量。利用MATLAB 画出频率与波数图像。充分反映其频率间隙的差异大小，利用该规律为工程实践提供理论指导，取得相应的社会经济效益。

1 弹性波在非线性结构的传播模型的参数设计与性能分析

非线性声学超材料用质量-振子链表示，如图1所示。每个单元格由一个刚性质量m1、一个非线性弹簧，以及一个由质量m2和一个线性弹簧k2组成的内部振子。非线性弹簧其刚度由一个线性刚度k1和一个五次方非线性参数Γ控制。单元格的长度为a。对于弱非线性弹簧，我们引入了一个小参数ε，使非线性弹簧中的恢复力fr可以表示为

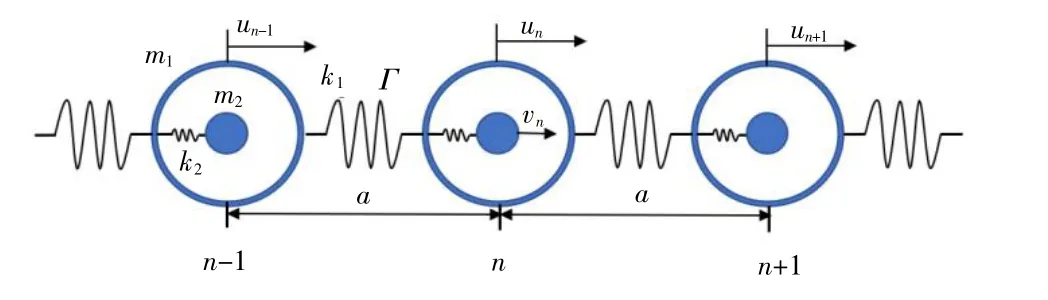
图1 具有非线性内刚度的振子的质量系统

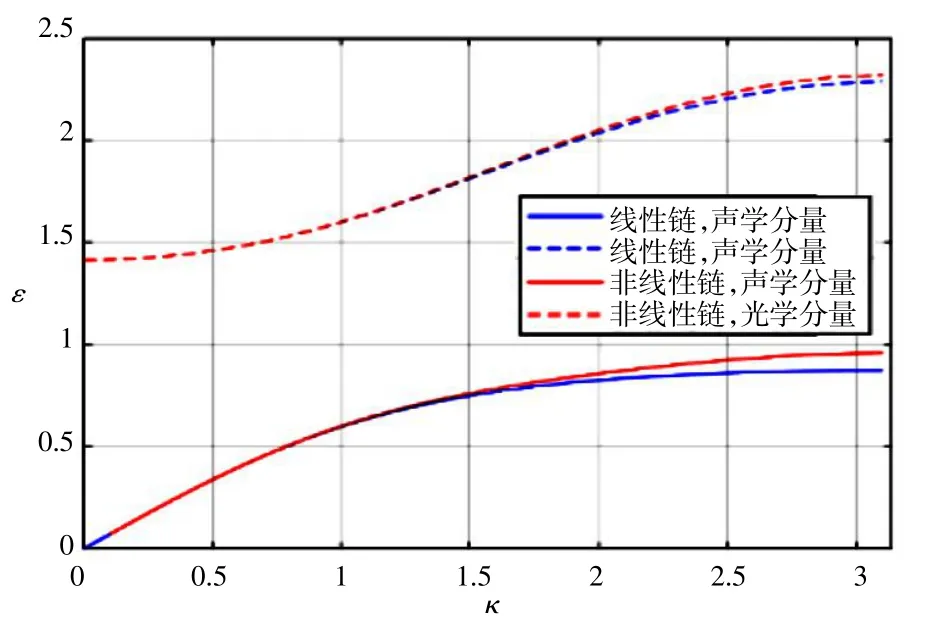
图2 用解析方法和数值方法预测的色散曲线

其中，δ为每个单元格产生位移。质量-振子链在无外力情况下的归一化运动方程可以写为：

其中，un和vn分别表示第n个外质量和内部振子的位移，（·）表示对时间t的导数。=Γk1，ωd=同时，为了方便计算。根据精度的需求，本文非线性参数最高阶次取1，设

其中，T=εt，将对T0求导记为D0，对T1求导记为D1，即

将式（4）（5）（6）（7）带入式（2）（3）中，可以得到如下方程两个方程

这里我们分离出式（10）中ε0和ε1系数，可得到两个方程，将ε0对应的方程作为控制方程，即

根据式（10）（11）可以假设

其中i=，κ=qa为无量纲波数，q为波数，a为相邻两单元之间的距离，c.c表示前面所有项的共轭复数，A和B分别代表单元外质量和内质量的波幅。将式（12）（13）带入式（11）中经化简可以得到

将式（12），（13），（14）带入（10）中可以得到

对其使用欧拉公式可求得决定ω0和κ之间关系的线性方程

不难确认，上述方程有两个正实根，将得到的较小实根对应系统的声学分量，记为ω0ac，较大实根对应系统的光学分量，记为ω0op。将式（8）（9）含有ε一阶的数的系数提取出来，形成修正方程，并将（12）带入可得

为了避免久期项的存在，令einκ eiωT0的系数为0，可得到方程

令b=（2 -e-iκ-eiκ）3，根据式（19）可以将D1A用b表示出来

将A用复数形式设出

其中α和β均为T1的函数。将A对T0，T1求导，可以得到

因为A是T1的函数，所以，D0A= 0，将式（20）带入式（22）中，并分离实部和虚部，得到α和β的一阶常微分方程

我们可以得到非线性频率ω与κ之间的方程

图中可以发现声学分量的最大值与光学分量最小值之间存在一段频率间隙，范围是（0.9025 <ω <1.4142）。

2 非线性波动行为分析

2.1 非线性波动行为分析方法

考虑一个有500 个单元的不含阻尼非线性系统，如图3 所示。链两端采用PML（perfect matched layer）。

图3 500 个单元的不含阻尼非线性系统

在PML 上n从1 开始，到Npml结束，Cmax为PML上的最大阻尼系数。输入信号为一个Hann 调制的Ncy周期脉冲，初始位移和速度的函数为：

在这里，我们选择初始速度剖面来抑制左向波，H（n）是Heaviside 函数，U（n）函数为

2.2 非线性波动的空间特征

为了监测输入信号的波空间演化，考虑瞬态波在有限长度的不含阻尼非线性系统中的传播，初始条件采用式（27）（28）（29）（30）和式（32）（33）表示，用ODE45 对非线性系统进行模拟计算，计算模拟时间t= 500 s 后得到了模拟后不含阻尼非线性系统的声学波包。

如图4 所示。其中系统几何参数为：单元长度L=0.1，不含阻尼非线性系统的材料参数为：质量块质量m1= 1，线性刚度k1= 1，振子质量m2= 1，线性刚度k2= 1，振子激振角频率ωd= 1 rad/s。垂直坐标是标准化位移u/A0，水平坐标则是不含阻尼非线性结构系统单元格数。蓝色曲线、红色曲线、橙色曲线3 条曲线分别对应于初始波数为κ= π/9，κ= π/2，κ= 7π/9的波包。3 个图分别对应非线性参数4= 0（不含阻尼线性系统），4= 0.01 和4= 0.02 三种情况。对于非常小的波数κ= π/9，波包不受色散的影响，在系统中传播时没有任何失真。非线性对波包的影响在这一区域也是可以忽略的。当波数增加到κ=π/2 时，非线性对波包的影响同样很小。当波数增加到κ= 7π/9 时，表现为波包的伸长和振幅的降低。

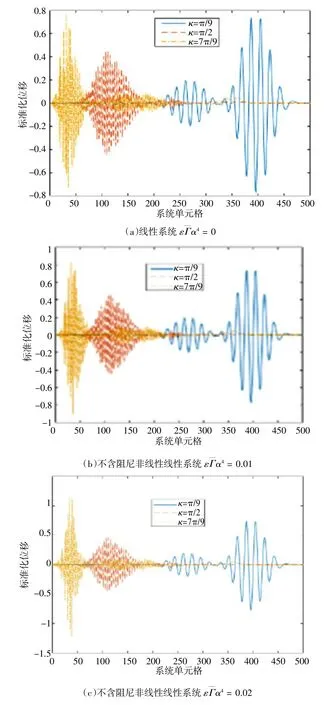
图4 对声学波包的空间剖面进行了不同值的非线性模拟

3 结语

通过MATLAB 对质量-振子系统绘制了色散曲线，由图中可得与声波模相比，光模对刚度非线性更为敏感，特别是对较高的波数。在对声学波包进行模拟后，对于非常小的波数，随着非线性参数的增大，振幅也增大，当波数变大，非线性参数对波包的影响变大，振幅增大。