基于三角函数拟合的改进型S 型加减速算法设计

孟宝星，王成勤

（徐州工业职业技术学院，江苏 徐州 221140）

0 引言

步进电机的转动是通过电机驱动器产生控制脉冲信号实现的。电机驱动器会产生不同频率和数量的脉冲来控制步进电机的速度和位移[1]。目前国内外常用的电机控制器的加减速曲线有：梯形加减速曲线、分段线性加速曲线、指数加减速曲线以及S 型加减速曲线，其中梯形加减速曲线原理简单，速度为时间的一阶导数，实现容易，能满足绝大应用场景，具有较高的性价比，应用广泛。但是由于梯形加减速的加速度为常量，即加加速度为冲击函数，会对电机造成不必要的柔性冲击，影响电机的使用寿命。一些高性能的电机控制器会采用S 型加减速来解决梯形加减速存在的问题。S 型加减速模式虽然优于梯形加减速模式，但其仍然存在加加速度突变，会对系统造成一定程度的振动，更重要的是S 型加减速模式在求解过程中存在多阶函数，其运算量较高且复杂，而传统的步进电机控制需要高达上千赫兹的脉冲发生速度，这会消耗较大的运算资源，这使得采用S 型加减速的驱动器成本相对偏高[2]。

蔡娜等[3]设计了一种新的可实时实现的抛物线型速度给定算法。这种算法响应速度更快，控制精度更高，减少了失步、过冲现象的发生率，避免了机械柔性冲击，但对系统要求仍然较高。周黎等[4]提出了一种“正矢型”加减速曲线，实现了对步进电机的精准控制，减少了失步过冲现象的发生率，但动态响应速度较慢。

1 步进电机控制系统概述

步进电机常用于各种运动控制系统当中，是一种常用的控制执行部件，主要有反应式、永磁式和混合式三种类型。从绕组数目分类来看主要有两相、三相和五相步进电机。目前市面上最常见的步进电机为两相混合式步进电机，大约占有97%以上的市场份额。主要针对两相混合式步进电机系统进行讨论。

步进电机驱动器，是一种将电脉冲信号转换为电机角位移的驱动执行器。如图1 所示。由于步进电机本身是运动部件，在运动过程中会产生惯性。在步进电机控制的过程中，速度不能发生突变，否则会对其机械结构产生较大的冲击，一般称其为刚性冲击。如果加加速度产生突变，也会造成电机磨损。最理想的情况是：电机运动的速度、加速度及加加速度皆连续且可导，可以最大程度的避免电机运行过程中造成电机的磨损。这也是在步进电机驱动过程中需要引入电机加减速的原因。

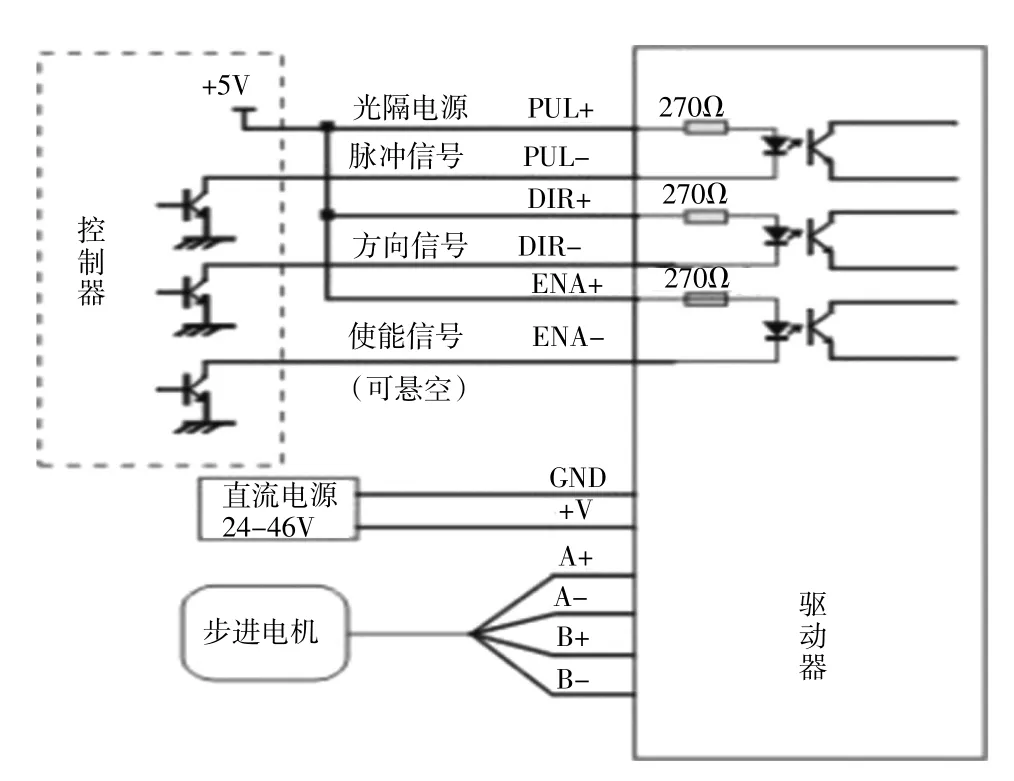
图1 步进电机驱动器结构框图

分析了传统S 型加减速的基本原理，并分析了它存在的局限性。为了解决上述问题，引入了改进型的S 型加减速算法，利用三角函数拟合S 型加减速的变加速阶段，将三角函数的导数转换为移位运算，从而显著降低算法的计算量，具有较高的适用性。

2 传统S 型加减速算法解析

S 型加减速曲线名称是由系统在加减速阶段的速度曲线形状呈S 形而得来的，采用降速与升速对称的曲线来实现升降速控制。正常情况下的S 曲线运行过程可分为加加速段、匀加速段、减加速段、匀速段、加减速段、匀减速段和减减速段7 段。在变加减速区，加速度的导数为恒值；恒加减速区，加速度为恒值；匀速段的速度为恒值，加速度为零。S 形加减速在任何一点的加速度都是连续变化的，从而避免了柔性冲击，速度的平滑性很好，运动精度高[2]。

根据加减速阶段的7 段模型，设S为行驶位移，J为加加速度，A为加速时加速度，DA为减速时加速度，Vmax为电机的最大速度，Vs为电机的起始速度，Ve为电机的终止速度，fa为加速度函数，fj为加加速度，fv为速度函数，fs为位移函数。在S 型加减速模型中A不是固定值，所以可以设置Amax为加速时最大加速度，Dmax为减速时最大加速度，同样在设定Amax=Dmax，Vs=Ve的情况下进行讨论，其他方向上同理。

标准的S 型加减速是以加加速度为恒定值来进行建模，所以fj的函数表示如下：

由此可以得到fa的函数表达为：

定义一组数值代入公式可以得到相应的函数曲线，假设J= 200，Amax= 100，Vmax= 200，Vs= 30，S=0，便可以画出fj和fa，以及fv和fs的函数图形，如图2、3 所示。

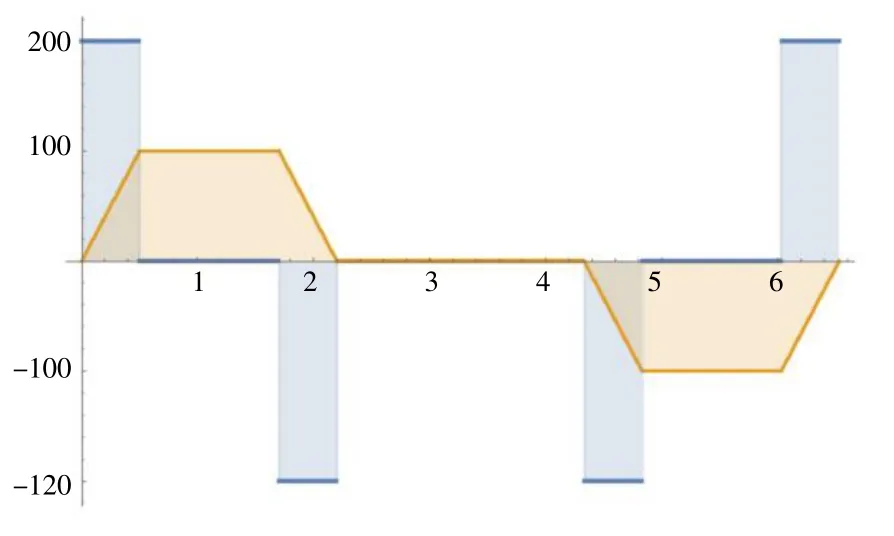
图2 S 型加减速fj 和fa 函数图形

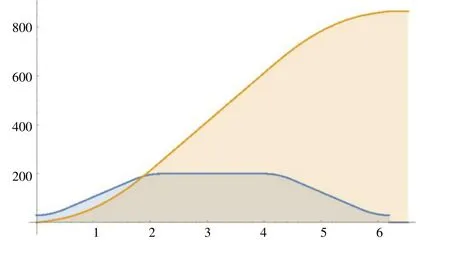
图3 S 型加减速fv 和fs 函数图形

通过仿真得到了S 加减速的模型，但是同时也发现在计算fv的公式中出现了大量的4 次方的运算，在执行S 型加减速的计算过程中需要频繁的进行开四次根的计算，由于在实际应用过程中电机控制的脉冲频率一般可以达到200 K 左右，这需要强大的算力保障，且S 型加减速依然存在加加速度的突变，在一定程度上也会造成设备的振动。故此一般传统的低端步进电机控制产品普遍采用梯形加减速算法，而没有采用S 型加减速算法，这样的确降低了控制器成本和研发难度，但是也导致了电机的性能和寿命的降低，稳定性也受到了不小的影响[5]。

3 改进型S 形加减速算法设计与实现

通过上文的分析，可以看到S 型加减速的基本原理及其存在局限性，S 型加减速的局限性主要在于其加加速度依然存在突变，这样依然会在一定程度上导致设备的振动和磨损，且S 型加减速算法的运算过程中存在4 阶函数，其在工程应用中对控制器的性能提出了较高的要求，这样大大提高系统的复杂度和成本。

S 型加减速存在的问题主要存在于7 段控制模型中的加加速模式和减加速模式，在S 型加减速算法中，引入了加加速度J的概念，且在加加速和减加速状态下J为常量。如果把J从常量状态定制为多阶可导的三角函数模型，便从数学建模的角度解决了加加速度突变的问题。

所以在改进型的算法中，引入Jmax为最大加加速度，并在加加速度阶段设定加加速度的曲线定义为：

其中定义：

上文中t3时间段为电机在保持Vmax匀速运动的阶段，所以可以通过积分计算出加速和减速时间段的位移，假设加速阶段的位移为Sa，减速阶段的位移为Sd，则可以得到：

通过上述算式可以发现，当t = t1时，J= 0。这样便确保了加加速度的连续性，依次代入t=t1+ t2，t= 2t1+ t2，t=t1+ t2，t= 2t1+ t2+ t3，t=3t1+ t2+ t3，t= 3t1+2t2+ t3几个时间点，均可以得到J= 0。这样确保了加加速度的连续性，根据fj的函数表达，可以得出fa的函数表达为：

代入t在各个时刻的值，可以发现加速度A依然连续且可导，然后根据加速度函数便可以得到速度的函数表示如下：

得到速度函数带入求速度对时间的积分，得到位移。

定义一组数据Jmax= 200，Amax= 100，Vmax= 200，Vs=Ve= 30，S= 800，便可以画出fj和fa，以及fv和fs的函数图形，如图4、5 所示。

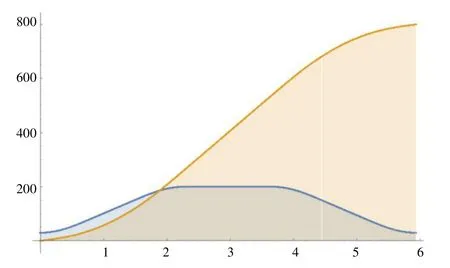
图5 改进型S 型加减速fv 和fs 函数图形

在实际的求解过程中可以发现整个函数本身还是遵循梯形加减速的加速、匀速及减速三个阶段，S型加减速是指把加速阶段又分为加加速阶段，匀加速阶段和减加速阶段，减速阶段为加速阶段相反。且在三角函数拟合的S 型加减速中，是根据加速阶段和减速阶段的位移，得到匀速阶段的位移情况，最终计算出匀速阶段的时间。所以在求解的时，可以把加速阶段，匀速阶段和减速阶段分别求解。举例说明如下：

例如在2t1+t2+t3开始的减速阶段，定义其实时间为2t1+t2+t3，定义该时间变量为tt，便可以得到：

该函数与加速阶段的函数基本一致，支持改为负值。这样便可以把整个三角函数分为3 段进行分析的话，可以大大减小运算量，如果在硬件计算中引入并行计算，便可以大大提升系统的运行效率，满足实时性、精度和资源占用等方面的要求[6]。

4 改进型S 形加减速中的三角函数求解问题

改进型S 型加减速算法，其需要的计算均为三角函数计算，可以通过查表法将三角函数求导转换为移位运算。其思路如下：要计算一个角度θ的三角函数值。首先，选择一个初始的量（x0，y0），通常设为（x0，0），表示初始角度为0 的向量，x0的值一般根据经验选择，特定的值可以在保证一定精度的前提下减少迭代的次数；然后，将目标角度θ分解成一系列旋转操作，每次旋转一个小的角度。在每次旋转之后，通过缩放操作来逼近目标角度的三角函数值。

因为数据的右移n位相当于乘以2(-n)，于是可以将初始缩放因子设置为1，0，每次迭代减半，假设缩放因子为gain，便可以得到

其中，d表示旋转方向（或者），矢量（x0，y0）逆时针旋转角度得到的值的表达式为：

因把cosθ去掉不影响求值的结果，得到：

以tanθ作为缩放因子，建立一个缩放因子表格，建立从2(0)，2(-1)，2(-1)的表格，然后通过迭代查表，便可以计算出θ的角度值。

表1 为设置最高17 次迭代的缩放因子表格。

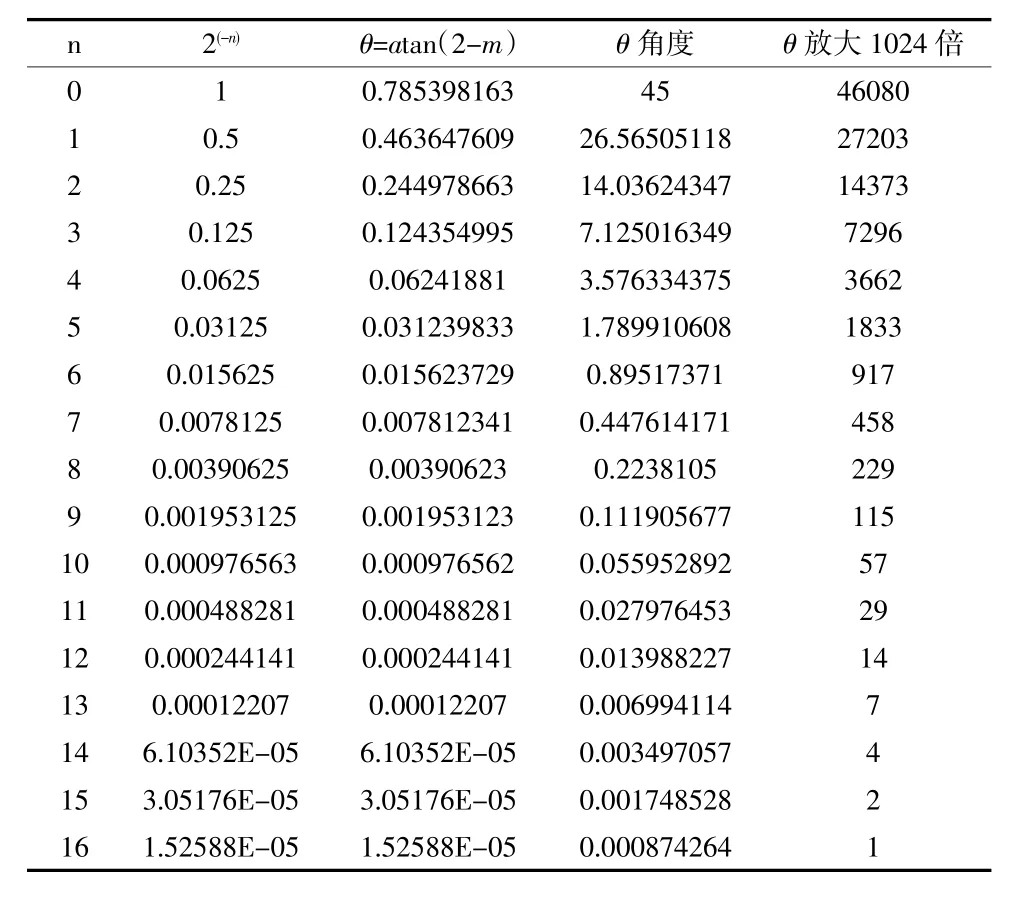
表1 缩放因子表格

表1 除了计算缩放因子对应的值，还把求取角度之后放大1024 倍的取整值也给出，目的是考虑到在嵌入式环境中，对浮点数的运算比较耗费时间，且1024 也刚好是数据左移10 位的值。如便可以简单实现三角函数的快速实现，

下面是该算法的核心部分C 语言代码：

include

#include

#define M_PI 3.14159265358979f

#define TABLE_SIZE 17 // 迭代次数

//按照角度扩大1024 倍运算

static const int atanTable [TABLE_SIZE] = {46080，27203， 14373，7296，//83662，1833，917，458，//128229，115，57，29，//204814，7，4，2，//327681 }；

// Cordic 算法计算正弦和余弦

//最小值：0.001，小于这个值为0 度，不需要判断

void cordic（double angle，double*sinVal，double*cosVal）

{

int x = 35628;

int y = 0；

int z = 0；

int nextX，nextY，nextZ；

angle = angle*180 / M_PI；

int unit =（（int）angle））/ 90；

angle =（（int）angle））% 90；

z =（int）round（angle*1024）；

for（int i = 0; i < TABLE_SIZE; i++）

{

if（（abs（z）<= 1）

{

break;

}

else if（z ＞0）

{

nextX = x -（y ＞＞i）;

nextY = y +（x ＞＞i）;

nextZ = z - atanTable[i];

}

else

{

nextX = x +（y ＞＞i）;

nextY = y -（x ＞＞i）;

nextZ = z + atanTable[i];

}

x = nextX;

y = nextY;

z = nextZ;

}

double val = sqrt（（double）x*x +（double）y*y）;

switch（unit）

{

case 0：

*sinVal =（（double）y）/ val;

*cosVal =（（double）x）/ val;

break;

case 1：

*sinVal =（（double）x）/ val;

*cosVal = -（（double）y）/ val;

break;

case 2：

*sinVal = -（（double）y）/ val;

*cosVal = -（（double）x）/ val;

break;

case 3：

*sinVal = -（（double）x）/ val;

*cosVal =（（double）y）/ val;

break;

}

}

int main（）{

double angle = -20.0*M_PI/180; // 待计算的角度，以弧度为单位

double sinValue，cosValue;

cordic（angle，&sinValue，&cosValue）; // 使用Cordic 算法计算正弦和余弦

printf（"Angle：%.2f "，angle）;

printf（"Sin：%.4f "，sinValue）;

printf（"Cos：%.4f "，cosValue）;

return 0;

}

以下是一段基于cortex-M3 内核的控制器执行效率对比代码，以0.01 弧度作为单位，对0-6.28 进行正弦和余弦计算，如下：

angle = 0;

runtime_start（）;

for（i = 0; i < 628; i++）

{

angle += 0.01;

cordic（angle，&sinValue，&cosValue）;

}

runtime_stop（）;

printf（"cordic time：%d. "，（time_cnt<<16）|runtime）;

angle = 0;

runtime_start（）;

for（i = 0; i < 628; i++）

{

angle += 0.01;

sinValue = sin（angle）;

cosValue = cos（angle）;

}

runtime_stop（）;

printf（"math time：%d. "，（time_cnt<<16）|runtime）;

测试的结果如下：

三角函数转化位移时间为：11971 个机器时间周期；

普通三角函数运算时间为：58413 个机器时间周期。

可见在传统的嵌入式系统当中，采用三角函数转换为移位运算的执行效率，为普通三角函数运算性能的4.8 倍。

5 结语

在步进电机控制系统中为了解决电机在运行过程中会产生刚性冲击、柔性冲击以及加加速度突变产生的设备振动问题，对传统的加减速模型进行改进，根据三角函数多阶连续可导的性质，引入三角函数曲线拟合，提高系统的稳定型，且在运算性能有限的场景中，也可以快速的利用查表法进行三角函数的求解，把三角函数运算转化加减和移位运算。避免了不必要的快速浮点和求阶运算，大大提升了系统的运行效率，降低系统的成本。