基于改进粒子群的作业车间调度多目标优化方法
2023-10-24魏宏静魏宏钰
魏宏静,魏宏钰,黄 彪
(1.贵州理工学院机械工程学院,贵州 贵阳 550003;2.铜仁职业技术学院经济与管理学院,贵州 铜仁 554300)
0 引言
当前,制造技术和科学技术的快速发展,制造规模和复杂度都在迅速提高,在市场上的竞争也越来越激烈。为了使企业在市场上取得更大的成功,就需要对整个企业、各车间、各生产环节做出更加有效的计划安排。在最近的几十年里,由于制造技术、信息技术、自动化技术等得到了全面的综合应用,许多先进的制造模式相继出现[1]。尽管现有制造模式在原理上和实现技术上都存在较大差异,但每一种制造方式都需要实现对内外资源的优化配置,以此才能够实现对制造周期的缩短和对生产成本的控制,从而要解决当前大部分企业所面临的共同问题,从而提高企业在市场上的竞争力。作业车间调度作为整个先进制造结构体系实现和核心,其实质是在一定时间内,将可利用的共享资源、生产任务等进行合理的分配和排序,并使其达到期望的特定的性能指标。以最优的工作车间计划为目标,能够帮助企业在经济效益和资源利用向着更积极的方向发展[2]。同时,有效的作业车间调度优化也是实现提升生产效率和先进制造的基础与关键。基于此,为促进企业竞争实力提升,本文结合改进粒子群算法,开展对作业车间调度多目标优化方法的设计研究。
1 构建多目标作业车间调度目标优化模型
从作业车间的生产实际角度出发,以生产周期,交货满意度,生产成本,加工设备利用率为指标,制定最优的生产计划[3]。针对不同调度优化目标,确定对应的量化指标,如表1 所述。

表1 作业车间调度优化目标与量化指标对照
针对表1 中记录的各项量化指标,明确其具体的求取公式,并完成对各项指标目标函数的构建。产品制造周期内的最长完工时间指标y1的计算公式为:
式中,N为待加工工件类型总数;n为待加工工件种类;Tn为某一类工件n的完成时间。拖延惩罚系数y2的计算公式为:
式中,ETn为某一类待生产工件n在作业车间中生产产生的延误时间。公式中,ETn可通过下述公式计算得出:
式中,DTn为某一类待生产工件n的交货日期。加工成本y3的计算公式为:
式中,vm为单位时间内某一机床作业时所消耗的费用;sm为单位时间内某一机床闲置时所消耗的费用;t0为某一待加工工件在某一工序上所消耗的时间;x0为决策变量;M为调度方案中规定的最大完成时间。机床最大负荷y4的计算公式为:
在公式(4)和公式(5)中,当x0的取值为1 时,此时某一类待加工工件第某工序在机床上进行加工;当x0的取值为0 时,此时为未选中状态。根据上述公式,确定多目标作业车间调度目标优化模型Y的表达式为:
进一步确定各项量化指标与目标Y之间的关系为:y1、y2、y3与Y为负向相关;y4与Y为正向相关,即y1、y2、y3越小,y4越大,作业车间调度优化效果越理想。
2 基于改进粒子群的调度问题编码
为了解决调度问题,在调度问题编码中,首先将染色体的位置向量与排程规划相对应。优化调度问题求解的满意程度和算法的复杂性都与编码质量密切相关[4]。在编码的过程中需要考虑到编码的可行性以及有效性。把调度编码过程的顺序,每一个基因都表示代工生产的过程[5]。在此基础上,根据每个工艺点在已知染色体颗粒上的排列顺序,确定每个工艺点的个数。假定Job Shop 排序问题有n个工件数,那么改进粒子群中的每一条染色体都包含n×m个完整的基因,每一条工件数都是m次,这里的基因是对工件数进行排序的,并不是对工件数进行详细描述[6]。以包含3 个机器,3 个工件的Job Shop 调度为例,见表2。

表2 包含3 个机器3 个工件的Job Shop 调度案例
针对表2 中的3 个机器3 个工件的Job Shop 调度案例,其改进粒子群编码如图1 所示。
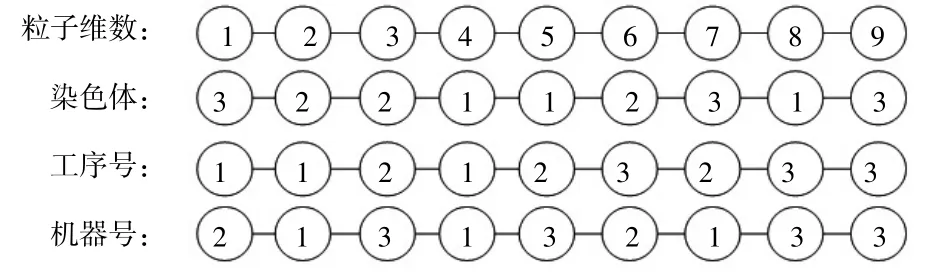
图1 改进粒子群编码
在对调度问题编码时,随机生成9 维(3×3)染色体颗粒。1,2,3 分别代表相应的工件j1、j2、j3的工序号。因为每一个产品都包括3 个步骤,所以每一个整数表示产品在一个染色体上的三次发生。在译码过程中,首先利用修正的质点向量来判断各工艺的加工机理,并将相应的质点向量转化为顺序操作表。两种的顺序决定着工序调度的优先顺序,再依据表2 中的内容,按照工序的先后次序,按照工序的最短容许时间,对所分配的机床进行加工,进而得到调度方案。
3 粒子位置更新策略与最优解搜索
在完成对调度问题的编码后,结合改进粒子群算法,确定粒子位置更新策略,并搜索调度最优解。通过对微粒群算法进行优化,得到微粒在微粒演化过程中,微粒在当前状态下、个体最佳状态与种群最佳状态相互影响的变化规律。通过模仿构建上述三个部分,基于改进粒子群算法的优化机制,定义离散粒子群粒子位置更新公式:
式中,Xki+1为离散粒子群粒子位置更新结果;c1为认知系数;c2为社会系数;ω为惯性权重因子。利用对染色体粒子进行的编辑运算,对其搜索空间进行拓展,从而指导粒子进行进化。最终确定最优解。主要变异方式包括:交换变异、插入变异和反序变异。在改进粒子群中,通过在p 位、q 位两个位点,在不改变其他位点的情况下,将两位点上的基因进行互换。本文中的互换运算使两个位点上的基因不完全一样,从而避免两个位点上的基因完全一样的可能[7]。在该方法中,通过对染色体颗粒中的p、q 个基因进行随机选取,并将其插入到相应的位置。逆序突变是指在两个不同的位点上,在两个位点上进行一次突变,然后将两个位点上的基因重新插入到两个位点上[8]。在此基础上,提出了一种基于微粒群的离散微粒群优化方法,该方法具有微粒群优化方法收敛快、易于实现等特点。然而,在具有有限的搜索迭代次数和粒子数的条件下,调度问题的规模越大,可供求解的空间也就越大,算法不可避免地会陷入局部最优,而不能完全绝对地保证每次都能搜索到全局最优。利用改进粒子群算法中的局部搜索策略,对作业车间调度多目标优化问题进行最优解搜索。在执行完成一次粒子位置的更新操作后,针对中群众的适应度数值在前10%的个体以及其他任意20%的个体进行最优解搜索。在相应点上,采用了一种基于交变邻居结构的最佳搜索策略,实现了对相应点的局部搜索。在具体对作业车间调度多目标优化求解时,设定初始参数。通过对PSO 的恒定惯性权数、认知因子、社会因子进行初值,并对最大迭代数和群体大小进行计算。采用基于步骤表示的编码方式,对群体和染色体进行随机初始化,生成群体和染色体颗粒。通过对每一个微粒进行译码,得到微粒在译码过程中的适合度,并将该适合度作为优化问题的一个目标函数,记录下微粒在初始状态下的局部最优和整体最优。更新粒子位置,并同时更新各个粒子的局部最优值和全局最优值。在该算法中,对个体的适应度最高的10%和其他20%的个体进行局部寻优。在此基础上,对每个粒子进行局部最优和整体最优。判断是否达到进化停止条件,若是,则输出求得的最优值结果,并退出循环,否则重复上述操作步骤,直到确定最优解为止。对离散微粒群算法的改进,是以基本微粒群算法的演化优化机理为基础的,与遗传算法的优胜劣汰的演化机理完全不同。根据上述操作,完成对作业车间调度多目标的最优解搜索,将最优解作为最终的作业车间调度方案。
4 优化前后对比
在上述论述基础上,为验证引入改进粒子群算法的目标优化方法是否能够实现对作业车间调度的多目标优化,选择以某生产制造企业的作业车间为研究对象,针对其日常作业任务进行调度。通过对比优化前后作业车间的生产周期用工件最大完成时间、生产成本、机床利用率等指标,对是否实现优化进行判定。该生产制造企业的作业车间生产规模是多品种、小批量的,属于流程式作业车间。在生产过程中集合了人、设备、材料以及能源等多种因素,生产过程中生产物料的连续性、生产工艺等约束的复杂性使得该作业车间的调度极为复杂。根据该生产制造企业对该作业车间的生产要求,确定生产周期最大完成时间应控制在18~20 天范围内;生产成本控制在15 元/m ~17 元/m范围内;机床作业率应控制在85%以上。根据上述标准,将应用本文设计的优化方法前后优化效果对比,得到结果见表3。

表3 优化前后作业车间调度结果相关参数记录
对表3 中记录的结果进行分析得出,优化后生产周期最大完成时间、生产成本明显降低,机床作业率明显提升,且三项指标均在该生产制造企业对该作业车间生产要求规定范围内。生产周期最大完成时间越短,生产成本越低,机床作业率越高,调度效果越理想。因此,通过上述得出的结果可以证明,本文提出的基于改进粒子群算法的优化方法能够实现对作业车间调度多目标优化,具备极高的应用可行性。
5 结语
针对作业车间调度问题,本文提出了一种基于改进粒子群算法的多目标优化方法。将该方法应用于实际可以使作业车间生产周期最大完成时间缩短,降低生产成本,并促进机床作业率的提升。通过研究得出,将改进粒子群算法应用到作业车间调度优化中可以缩小算法的搜索空间,使算法效率得到提升。同时,该算法还可以将求解的优化问题聚焦于决策所关注的范围内,从而有效地降低了非劣解个数,从而有效地解决了从一堆非劣解中搜索出最优解的难题。
