PID参数调整下水轮机水锤效应的实验分析

2023-10-24温苾芳魏蒙希李钦林龚晓静

科技风 2023年29期

关键词：水锤水轮机阻尼

温苾芳魏蒙希李钦林龚晓静

电子科技大学成都学院工学院四川成都 611731

2020年,我国水电年发电量突破1.20万亿kW·h,电力系统中水电占比日益增高[1]。与此同时,我国水电相对集中的西南电网中,超低频振荡现象日益明显,影响电网稳定[2-3]。

研究表明,水锤效应是引发超低频振荡现象的重要因素之一[3-4],而水轮机组多采用PID型调速器,研究PID参数调整对水锤效应的影响,对水电占比较多地区电力系统的安全稳定运行具有重要意义。

相关研究人员非常重视水锤效应引发的现象,对其机理开展研究。文献[5]在利用伯德图和阻尼分析法研究超低频振荡阻尼特性;文献[6]讨论了调速器参数对频率稳定的影响;文献[7]在单机无穷大系统中,研究水锤效应和输出功率对系统阻尼的影响。

本文首先推导水轮机、电动机及调速器等主要装置的数学模型,继而根据实际运行情况对各模型进行合理简化。随后在MATLAB/Simulink中搭建水轮机调速控制模型,研究PID参数与水锤效应间的关系,并在单机无穷大系统验证所得结论的正确性。

1 水轮机调速系统数学模型

水轮机调速控制系统由水轮机、PID调速系统、电液伺服系统、发电机等部分组成,系统调速过程框图如图1所示。

图1 水轮机调速过程框图

图中,ω0为额定转速,ω为实际转速,Δω为转速偏差,Pm为水轮机提供的机械功率,Pe为发电机输出的有功功率,PL为负荷有功。调速器利用Δω调节叶片开度,控制机组Pm,实现对Pe的调节。

2 水轮机调速系统设计

本文对水轮机调速系统进行仿真,探索水轮机调速系统的阻尼特性,研究不同调速参数下系统的运行特性。

2.1 调速系统阻尼特性分析

已知调速系统中各模块的模型后,探索调速特性与阻尼特性间的关系,系统特征方程如式(1)。

(1)

式中,Ds=D+KL,将式(1)表示为标准形式:s2+2ξωns+ωn2=0,其中ωn为无阻尼振荡频率,ξ为单机系统阻尼比,则ξ可表示为:

(2)

可知,水流惯性时间常数TW变大,系统阻尼减少,易产生负阻尼,影响系统稳定。

2.2 水轮机调速系统参数设计

在MATLAB中以传递函数,依次构建PID调速器模型、伺服系统模型、水轮机模型、发电机及负荷模型,并连接成完整的水轮机调节系统模型。

仿真图中,开关K1接入表示空载频率扰动仿真实验,开关K2接入表示负荷扰动仿真实验,系统各参数如下表所示。

调速系统参数表

2.3 调速系统空载特性分析

对水轮机组调速系统进行空载仿真,依次分析Tw、KP、KI、KD对系统特性的影响。

同一空载扰动下,保持其他参数不变,对不同TW仿真,观察系统水锤效应的影响,系统频率变化波形如图2所示。

图2 TW对系统频率的影响

由图2可知,TW数值较小时,调速器超调量很小;TW增大时频率变化增大。说明空载扰动下,TW越大水锤效应对调速系统影响越明显。

保持其他参数不变,对KP不同取值进行仿真,观察系统频率变化,波形如图3所示。

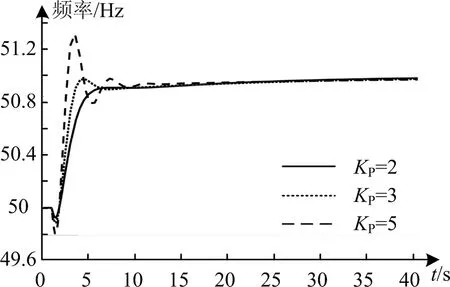
图3 KP对系统频率的影响

由图3可知,KP数值增大时频率偏差也增大,说明空载扰动下,KP越大水锤效应对系统影响越严重。

同理,对KI、KD不同取值进行仿真,观察系统频率变化。综上,空载频率扰动下,Tw、KP对水锤效应有较大的影响。此时,减小Tw、KP可减弱水锤效应,进而降低其对频率的影响。

2.4 调速系统负荷特性分析

水轮机调速系统进行带负荷仿真,负荷扰动下,依次令Tw、KP、KI、KD取不同值,观察系统频率,波形如图4所示。

(a)Tw的影响

由图4(a)可知,负荷扰动下增加Tw的值,频率幅值变化增大,表明水锤效应增强,对速度控制系统影响越大。由图4(b)可知,随着KP取值增大,频率偏差不断降低,且响应时间提前。由图4(c)可知,KI增大时,系统频率偏差有所回升,且恢复时间变短,表明负荷扰动下,KI抑制水锤效应效果有限,但一定范围内利于系统恢复稳定。由图4(d)中KD增大,左下角水锤效应幅值及后续频率波形均未表现出明显变化,表明实际调速中KD对水锤效应影响较小。