高等数学课程教学中的案例教学育人实践——以无穷小量的教学过程为例

舒亚东 吴隽永

贵州黔南经济学院 贵州惠水 550600

高等数学作为一门基础课程,对实现高质量教育有着重要的地位。好的课程设计是实现高质量教育和公平普惠的教育,使教育更加充满活力的主要手段[1]。高质量课堂不仅需要丰富的内涵,更肩负培养学生价值取向的使命[2]。高质量教育和立德树人为新时代赋予了特殊的内涵,也对新时代的教育改革指明了方向,必须以青少年理想人格塑造为核心[3]。本文以高等数学一次课的教学内容(无穷小量的定义及性质)为例,通过构造丰富的案例,把育人教学贯穿整个课堂教学过程。

一、教学目标

知识目标:正确理解无穷小量的概念(包括直观概念和几何概念);掌握无穷小量的基本性质。

能力目标:培养学生自主探究能力和明辨性思维;通过对无穷小量概念和性质的理解,体会数学中极限的思想,实现极限思想与现实世界有机结合。

育人目标:通过中国古人对极限思想的贡献,激发学生爱国主义情怀和增强文化自信;培养学生用辩证的思维理解无穷小量的哲学内涵,引导学生树立正确的人生观、世界观,从而给学生提供强大的精神动力。

二、教学重点与难点

教学重点:无穷小量的性质以及无穷小量的应用。

教学难点:无穷小量的概念和性质。

三、教学方法和手段

(一)多媒体演示法

通过计算机动画演示,帮助学生有可视化的直观感受,清晰描述无穷小量的渐进过程。给出一些来回波动,但最终又向无穷小迈进的案例。

(二)启发式教学

通过励志人物传记,培养学习的爱国热情,增强文化自信,启发学生思考脚踏实地、坚持不懈努力的意义和内涵,从而培养学生努力学习、踏实做人的良好品质。

(三)问题驱动教学模式

以问题情境为导火索,通过问题环环相扣,使整个教学环节在不断激发学生的探究热情,引导学生分析问题、解决问题的过程中,达到本次课程的学习目的。

(四)课堂讨论

给出几个案例,先让学生分组讨论,然后诱导学生思考所给案例所隐藏的哲学内涵,从而让学生明白哲学不再是单纯的教条和苍白的文字,同时,数学也不再是枯燥无味,而是充满人生哲理的学科。

(五)总结发言

课程快结束时,让学生分组讨论总结本次课程的学习内容和要点。每一组选一个代表上台交流发言,这样可以提升学生课堂参与度,同时让更多的哲学道理给学生提供强大的精神动力。

四、教学实施过程

(一)回顾复习

1.首先介绍我国数学家对极限思想的贡献,进而激发学生的爱国热情,同时增强文化自信

我国数学家刘徽给出了“割圆术”,即割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣。也就是说通过圆内接正多边形细割圆,并使正多边形的周长无限接近圆的周长,该观点已经形成了极限思想的雏形,为现代极限概念的形成奠定了思想基础,在世界数学史上留下了浓墨重彩的一笔。直到18—19世纪,通过无数代数学家的努力,才形成严格的极限理论。然后通过动画给出极限的渐进过程。

2.回顾极限概念

数列极限的定义:

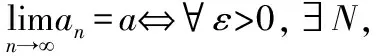
从定义中引导学生加强对ε和N的理解,为本次课程的主要内容无穷小量做好铺垫。

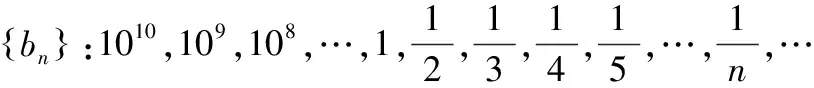
显然,无论是根据极限的直观定义还是严格的数学定义,上述两个数列的极限都为零。同时表明,假如这两个数列就代表两个人的成长轨迹,无论起点怎么样,只要后续不努力,终将一无所有。也或者说一个人的未来怎么样,主要取决于你未来是否会连续付出。

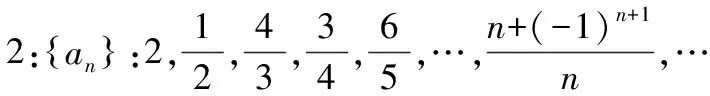
显然,该数列的极限为1,就像市场上商品的价格会来回波动,但随时间推移,终将会稳定在某一个确定的值。

函数极限的定义:

∀ε>0,∃δ,使得当0<|x-x0|<δ,恒有|f(x)-A|<ε.

(二)新知探究

1.通过动画和讨论,给出无穷小量的定义

给出《庄子·天下篇》中“截丈问题”的精彩论述:“一尺之棰,日取其半,万世不竭。”其含义是,一尺长的木棍,每天截去它的一半,千秋万代也截不完。显然,这句话包含了对立统一的思想。事物的发展总是先从量变开始,量变是质变的必要准备,质变是量变的必然结果。因此,我们做任何事情都要从一点一滴的小事做起,要脚踏实地、埋头苦干,积极做好量的积累,为实现事物的质变创造条件。让学生分组讨论该论述所表达的主要思想,从而得到在高等数学中占有重要地位的一个重要极限——无穷小量,然后给出无穷小量的严格定义。通过学习中国古代数学家对数学科学做出的重要贡献,培养学生的爱国热情和民族自豪感,同时增强文化自信。

无穷小量的定义:在某一变化过程中,函数以零为极限,即:

括号( )中的自变量可以是x,也可以是n,表达式中的过程主要有三类。若是数列极限,则该过程为n→∞;若为函数极限,则该过程可以是x→x0,也可以是x→∞。

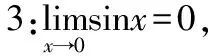
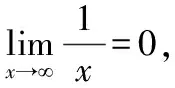
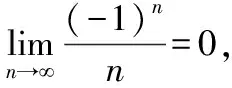
通过图像的轨迹可以说明无穷小量是一个运动的趋势,而不是一个具体的很小的数。

2.给出理解无穷小量的几点注记,同时举例解释

(1)无穷小量是变量,不能与很小的数混为一谈,即绝对值非常小的非零常数不是无穷小量。

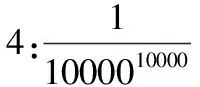
(2)零是特殊的无穷小量。

解释:特殊性在于零本身是常数,其极限就等于本身,也就是说零在任何过程中的极限都为零,根据定义,零是无穷小量。

(3)无穷小量总伴随着一个过程。

除了①和②,讨论任何变量是不是无穷小量,皆与过程有关。

例5:当x→1时,x-1,x2-1都是无穷小量,但当x→0时,x-1,x2-1都不是无穷小量。

在学习极限时,首先不是看函数本身,而是先关注变量的变化过程。

3.用PPT播放一些励志人物传记,诱导学生思考这些励志人物身上共同的基本素养,通过他人故事思考自己应该如何去度过自己的大学生活

这些平凡人物的身上都体现着脚踏实地、顽强拼搏、百折不挠的人生旅程。纵使经历无数失败,但为了理想,终其一生,最终实现了理想。

4.无穷小量的性质

性质1.有限个无穷小量的代数和仍然是无穷小量。

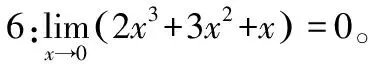
性质2.有限个无穷小量的乘积仍然是无穷小量。

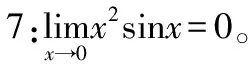
性质3.无穷小量与有界函数的乘积仍然是无穷小量。

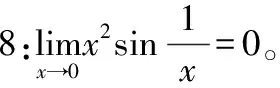
性质4.常数与无穷小量的乘积仍然是无穷小量。

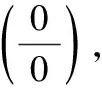
该例题表明:假如该数列就代表一个学生进入校园后的状态。纵然每次听课后感觉什么都没学到,因为每一项的极限都为零,是无穷小量,但该学生却选择了坚持下去,终将实现了量变到质变的蜕变。或者也可以说,只要坚持不懈付出终将会得到回报,付出是有收获的。

例10:当x→0时,x,x2,sinx都是无穷小量,让学生分组讨论如下极限:

显然,当把性质中的有限改为无限,两个无穷小量相除就可能得到不同的结论。

(三)无穷小量的应用

给出一些经典的案例,通过提问和分组讨论,引出无穷小量所蕴含的哲学意义。

提问学生,然后再提问其他同学对该答案是否认同,若认同,为什么?不认同,说明理由。显然,该例题中无穷个零的和还是零。

例题表明:假如该数列就代表一个同学进入校园后的状态,但整天做其他事情,从未走进过教室学习,那就意味着不付出是不会有收获的。

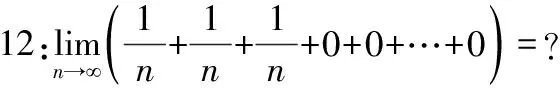
让学生分组思考,该例题和例11的区别在哪里?该例题带给我们什么启示?显然该例题的极限还是零。

该例题表明:假如该数列就代表一个学生进入校园后的状态。坚持听了几次数学课,但是每次基本什么都没学到,后面选择了放弃,但是和直接没来过教室的人相比,还是稍微要好点,只是说学到的东西几乎趋近于零,因此没有坚持几天就开始放弃了,导致的结局也是一无所有。即没有足够的耐心和恒心,是很难成功的,并不是付出不一定有收获,而是付出得还不够。

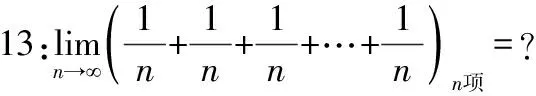
让学生分组思考,该例题和例12的区别在哪里?该例题带给我们什么启示?显然该例题的极限为1。

该例题表明:假如该数列就代表一个学生进入校园后的状态。纵然每次听课后感觉什么都没学到,但却选择了坚持下去,终将实现量变到质变的蜕变。或者也可以说,坚持不懈的付出终将得到回报。

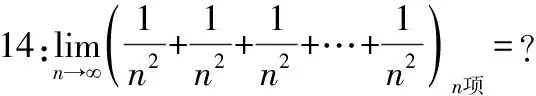
让学生分组思考,该例题和例13的区别在哪里?该例题带给我们什么启示?显然该例题的极限为0。

该例题表明:假如该数列就代表一个学生进入校园后的状态。和例13比较,该例题中学生每天学到的知识更少,或者说基础更差,且前者学习了n天,后者也只学习了n天,导致的结局是后者永远不如前者。同时告诉我们一个道理,假如我们本身不如别人聪明,结果自己付出和别人一样多,导致永远落后于别人。

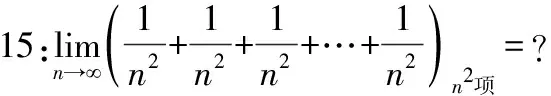
让学生分组思考,该例题和例13、例14的区别在哪里?该例题带给我们什么启示?显然该例题的极限为1。

该例题表明:假如该数列就代表一个同学进入校园后的状态。和例13比较,该例题中学生每天学到的虽然更少,但此时坚持学习了n2天,也就是说加倍努力,最终也实现了质的改变。该例告诉我们一个道理,假如我们本身不如别人聪明,或者基础没有别人好,那么我们就加倍付出,终将实现质的飞跃,最终取得成功。

上述例题再次表明,无穷个无穷小量的和不一定是无穷小量。

五、总结

总结本次课程所学到的知识点,可以给当代大学生四年大学生活或者说这一生提供一些启示。学生分组充分讨论,让数学课程包含的深刻哲学思维深入大学生的心灵深处,从而提供强大的精神动力和培养学生强烈的社会责任感。(1)大一新生进入新的校园生活,思想上有所松懈,比较迷茫,通过在一年级课程中引入饱含哲理的育人元素,增添学习的乐趣,使枯燥的数学变得有趣;(2)通过数学课引申出的哲学内涵无疑给学生注入了强大的精神动力,同时让学生明白有所为有所不为,坚定理想信念;(3)通过无穷小量的学习,使学生具有获得感。即使每天进步微乎其微,但是有了数学课验证下的量变累积到一定程度必然会发生质变和付出一定会有收获的科学内涵,从而营造良好的学习氛围。