基于LMI的分段线性系统共存吸引子转迁控制研究

李得洋, 吴少培, 李国芳, 丁旺才, 丁 杰, 俞力洋, 卫晓娟

(1.兰州交通大学 材料科学与工程学院,兰州 730070; 2.兰州交通大学 机电工程学院,兰州 730070;3.上海应用技术大学 轨道交通学院,上海 201418)

分段线性系统是一类很有代表性的非光滑系统,它广泛存在于实际机械系统[1-3]中,因此对此类系统的研究具有重要的理论意义和实用价值。由于此类系统具有非连续性或非光滑性,学者们主要通过解析、数值和近似解析的方法对系统周期运动的存在性、稳定性及混沌运动的生成及演化机理开展相应的研究。Shaw等[4]针对一类单自由度分段线性碰撞振动系统,通过建立系统的Poincaré映射,研究了系统周期响应的稳定性问题。Hu等[5]针对分段光滑系统,研究了非光滑向量场对系统Poincaré映射可微性的影响。利用数值和实验方法,Ma等[6]系统研究了四类弹性碰振系统在擦边点附近Poincaré映射的Jocobi矩阵特征值和迹的变化情况。Jiang等[7]把不连续几何方法从含刚性约束的碰撞振子应用到含弹性约束的碰撞振子中,研究了含单边弹性约束系统的擦边分岔。Miao等[8]应用中心流形定理,研究了一类考虑摇头阻尼非光滑的两自由度轮对的Hopf分岔类型及稳定性。Floquet理论是开展分段线性系统稳定性及分岔研究的理论基础,Leine等[9]给出了一般意义下分段线性系统周期解的Floquet理论,王强等[10]利用Floquet理论揭示了轴承外圈故障系统(等效为三自由度分段光滑系统)经Neimark-Sacker分岔通向混沌的路径。分段线性系统往往是一个多参数系统,在多个参数协同变化下,朱喜锋等[11]研究了一类两自由度含间隙约束碰撞系统周期运动的参数分布区域,并揭示了系统的颤碰运动特性。Li等[12]以含两种非光滑因素的碰撞振子为研究对象,研究了在参数平面上由擦边分岔等引起的黏滞运动、颤振运动和周期陷窝的形成机理;并进一步分析了高频区内系统共存吸引子及其吸引域的分布情况。

吸引子共存是非光滑系统的一种内在的特性,是指在给定参数下系统存在两种及两种以上的独立动态响应。鉴于分段线性系统对初始条件的依赖性,采用胞映射法可以更全面地探索此类非光滑系统在振动中的深层次问题。林何等[13]建立了功率分流直齿轮系统非线性振动模型,结合胞映射与区域分解思想构建了全局解域求解算法,揭示了系统的全局解域特性及各种潜在动力学行为。吴鑫等[14]针对一类受拟周期激励的具有悬臂结构的碰撞振动系统,研究了在参数变化下系统的奇异非混沌动力学及多稳态共存现象。Yue等[15]通过复合胞坐标系法,研究了一类含单边弹性约束碰振系统的吸引子、吸引域和混沌鞍等全局性态,揭示了内部激变和边界激变这两类激变的演化过程。张惠等[16]利用简单胞映射法,分析了含间隙及预紧弹簧激振系统由鞍结分岔、周期倍化分岔及边界碰撞分岔诱导出现的吸引子共存情况。Shen等[17]研究了一类非光滑系统(双频驱动的铰接式系泊塔模型)在初始条件变化时奇异的非混沌吸引子共存特征。

对于运动的主动控制而言,吸引子共存表明可通过初值扰动或施加外力实现具有不同动态特性的吸引子相互迁移。针对非光滑系统的共存吸引子转迁研究,学者们主要针对单自由度分段线性系统[18],文献[19]虽然利用线性反馈实现了一类两自由度含弹性约束非光滑系统共存吸引子的转迁,但对多态共存区的辨识及转迁机理未作定性分析,且对控制方法的稳定性及控制参数的选取未给出解决方案。本文以一类两自由度含间隙分段线性系统为研究对象,利用胞映射法和响应微扰计算方法对共存吸引子的分布及转迁开展研究;同时利用系统分段线性的特性,通过构造一组线性矩阵不等式来得到线性反馈控制器实现系统共存吸引子转迁的稳定性条件,仿真结果验证了本文方法的可行性和有效性。通过吸引子转迁控制可实现系统的减振、混沌控制和分岔控制。

1 系统的力学模型及运动微分方程

图1为两自由度含间隙分段线性系统的力学模型,质量为M1和M2的振子分别由刚度为K1和K2的线性弹簧以及阻尼系数为C1和C2的线性阻尼器连接,在简谐激振力Fisin(ΩT+τ)(i=1,2)(其中Ω、T和τ分别为激励频率、时间和相位角)的作用下沿水平方向振动。以系统的静平衡位置为空间坐标的原点建立坐标系,振子M1和M2的位移分别为X1和X2,在振子M1的右侧固定有刚度为K3的弹性约束。在简谐激励的作用下,当振子M1的位移小于D1时,系统为两自由度的线性振动系统;而当振子M1的位移大于D1时,振子会与右侧的弹性约束发生碰撞并接触在一起振动,由于间隙的存在和碰撞的产生,系统会表现出强非线性和非光滑的特性。

无量纲化有

(1)

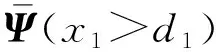
Ajsin(ωt+τ0)+Bjcos(ωt+τ0))(x1≤d1)

(2)

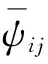
(3)

2 系统n-1周期运动的周期解

在系统稳定运动状态下,取振子M1与右侧约束面碰后瞬间为时间坐标原点(t=0),振子M1经历时间t1与右侧约束面脱离,再经历时间t2与右侧约束面再次碰撞,若t1和t2满足t1+t2=2nπ/ω,系统就存在n-1周期运动(用符号n-p表示系统的周期运动,其中n为激励周期,p表示振子以正向速度与右侧约束面碰撞的次数)。系统n-1周期运动的周期条件、边界条件和衔接条件可表示为

为便于周期运动推导,引入下列符号

n11=n22=cosωt1,n12=-sinωt1,n21=sinωt1

则系统n-1周期运动的周期解可表示为

(4)

CS=[cosτ,sinτ,cosτ,sinτ]T,

Q=[ψ11c1+ψ12c2,0,0,0]T,

将t=0及t=t1+代入式(4),可得积分常数关于初始条件的表达式

J=Φ1(0)-1(z(0)-M1(0)CS-Q)

(5)

(6)

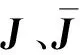
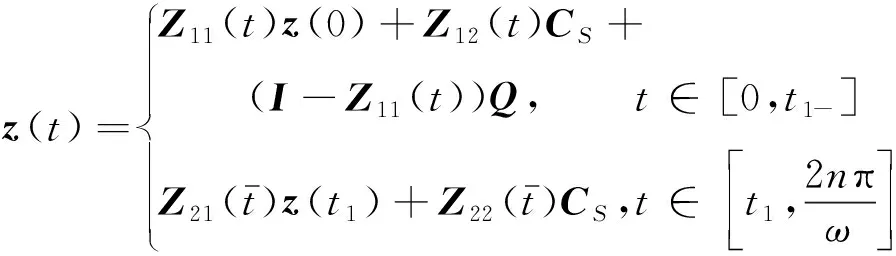
(7)

其中

Z11(t)=Φ(t)Φ(0)-1,

Z12(t)=M(t)-Φ(t)Φ(0)-1M(0),

(8)

其中

L=(Ι-Z21(t2)Z11(t1))-1(Z22(t2)+

Z21(t2)Z12(t1))=(lij)4×4;

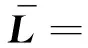
H=(Ι-Z21(t2)Z11(t1))-1Z21(t2)(Ι-

Z11(t1))Q=(hij)4×1;

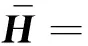
由初始条件x1(0)=d1,x1(t1)=d1可得初相位

τ=

(9)

τ=

(10)

其中

δ1=l11+l13,δ2=l12+l14,

根据初相位的表达式可得系统n-1周期运动的存在条件为

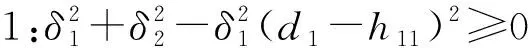
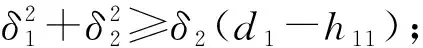
根据t1+t2=2nπ/ω,以及系统n-1周期运动的衔接条件,可得仅关于时间t1的表达式

(11)

通过数值方法可求解出方程的根t1,进而可确定系统n-1周期解。

3 系统Poincaré映射的建立及稳定性分析

为研究系统周期运动的稳定性和局部分岔问题,建立两个Poincaré映射

θ=mod(ωt,2π/ω)};

选择定相位面Σn可以统计出系统周期运动的周期数;选择约束面Σp可以统计出振子与约束面的碰撞次数。以定相位面Σn构造系统Poincaré映射,根据响应微扰计算方法[20]可得到系统的Floquet矩阵,具体计算步骤如下:

步骤1对系统进行求解,并确定其运动时间为nT(T为系统周期,n≥1)。

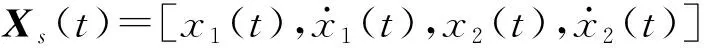
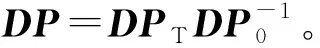
根据Li等方法可计算出系统的Lyapunov指数。Lyapunov指数既可确定周期和混沌运动的分布区域,又可甄别周期与混沌运动、周期与拟周期运动共存的区域,另外结合分岔图和Lyapunov指数图可研究各个共存周期运动在参数变化时出现的各种分岔。

4 基于LMI的线性反馈控制器稳定性分析

如图1所示系统施加线性反馈控制器后,被控系统可表示为

G(x1)=fsin(ωt+τ)

(12)

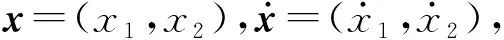
选取线性反馈增益矩阵

式中,u1、r和u2为控制参数。

将式(1)用一阶形式表示

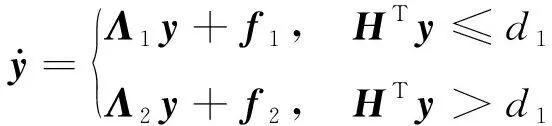
(13)

Λ2=

施加线性反馈控制器后,被控系统式(12)可表示为

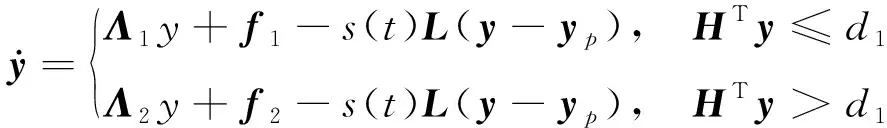
(14)

定义目标系统为

(15)

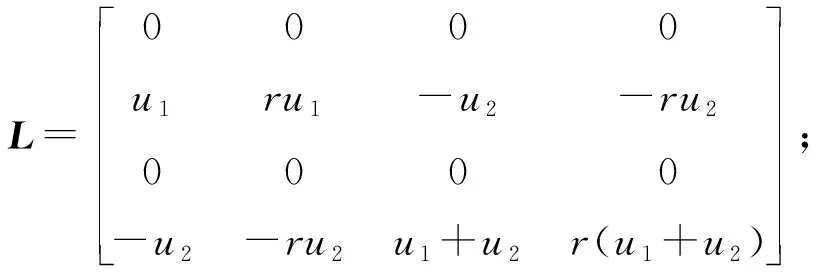
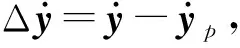
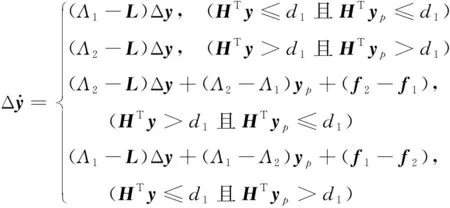
(16)

误差系统可简化的表示为

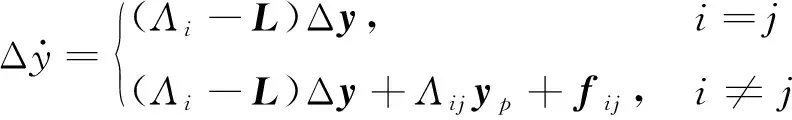
(17)

式中,i,j=1,2,Λij=Λi-Λj,fij=fi-fj。Λi和Λj符合下面的关系

Λi=Λj+GijHT

(18)

式中,Gij∈4×1。将Λi和Λj用向量Gij联系起来,可防止线性矩阵不等式在求解时出现半负定的情况。

为了证明误差系统的稳定性,建立如下的Lyapunov函数

V(Δy)=ΔyTPΔy,P=PT>0

(19)

由于目标系统和被控系统自身存在各个向量场之间的相互切换,为了降低保守性,在误差系统稳定性分析过程中,基于Lyapunov函数来构造稳定性条件;为了进一步降低保守性,将向量场信息通过S-procedure考虑进稳定性条件,使得式(19)所示的Lyapunov函数为正定以及其微分为负定的性质不需要在整个状态空间内成立,而只需要在对应的向量场内成立即可。

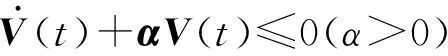
ΔyT[(Λi-L)TP+P(Λi-L)+αP]Δy≤0

(20)

当[(Λi-L)TP+P(Λi-L)+αP]≤0时,可保证式(20)成立。

若被控系统和目标系统分别出处于不同的向量场时有

(HT(yp+Δy)-d1)(HTyp-d1)≤0或

(HTyp-d1)(HT(yp+Δy)-d1)≤0

(21)

式(21)可表示为

(22)

当误差系统在HTyp-d1≤0且HT(yp+Δy)-d1>0或HTyp-d1>0且HT(yp+Δy)-d1≤0的向量场内,式(22)所示的Lyapunov函数是负定的。根据S-procedure,始终存在常数λ1>0和λ2>0使得下式成立

(23)

结合式(20),可得误差系统全局稳定的条件(即被控系统的稳定性条件)

当i=j时

ΔyT[(Λi-L)TP+P(Λi-L)+αP]Δy≤0

(24)

当i≠j时

(25)

(26)

式(24)、(25)和(26)是关于{P,L,λ1,λ2}的非线性矩阵不等式,但是关于{P,PL,LTP,λ1,λ2}的线性矩阵不等式。因此,利用线性矩阵不等式的相关求解器可有效地解决这些问题。如果存在矩阵P=PT>0,并且存在正实数λ1与λ2,满足式(24)、(25)和(26),则误差系统(16)是渐近稳定的,可以实现共存吸引子的转迁。

5 仿真研究与分析

5.1 系统共存吸引子产生及湮灭分析

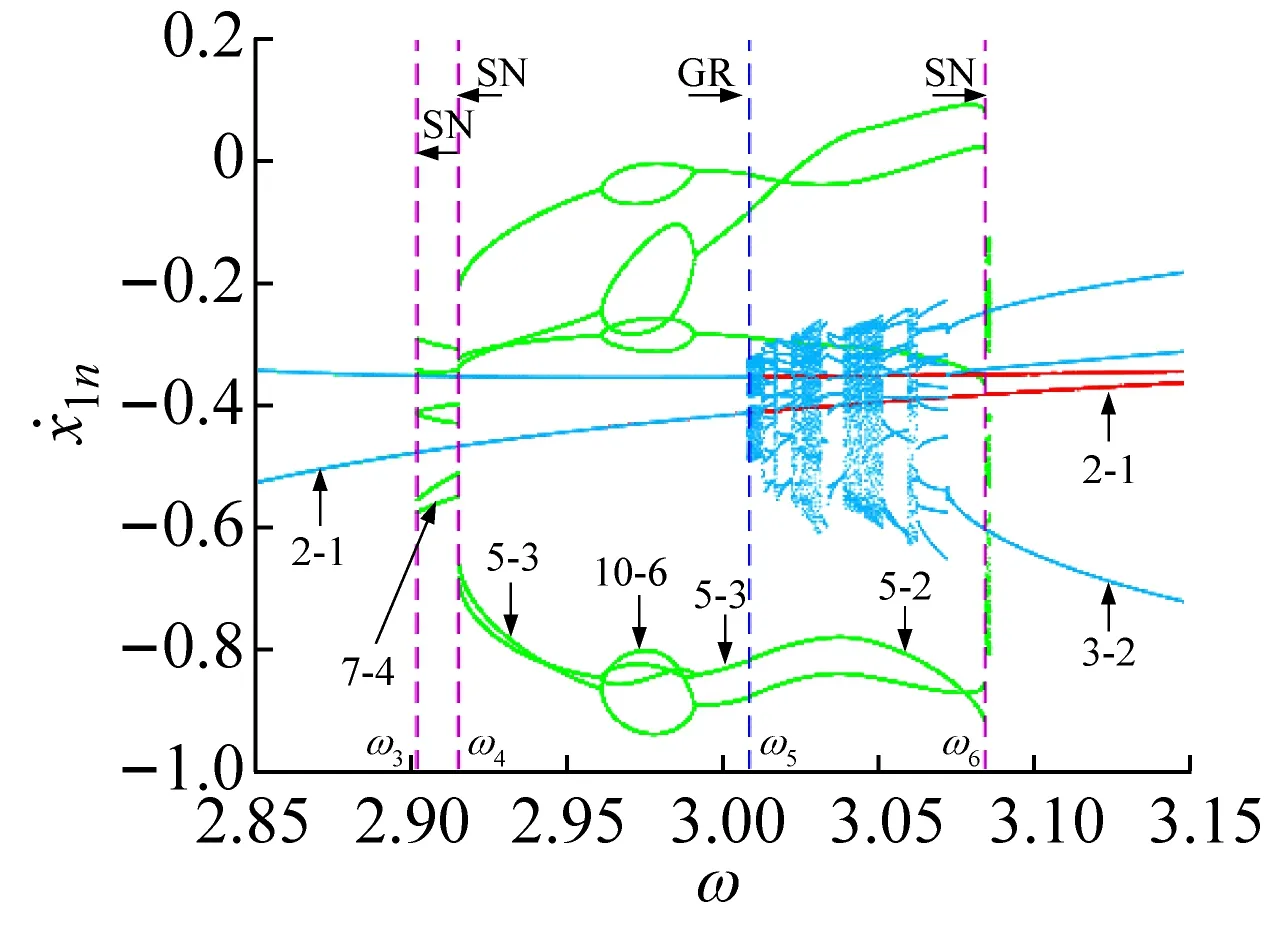
取基准参数①:ω∈[2,3.5],μm=0.5,ξ=0.1,μk2=0.7,μk3=0.95,d1=0.1,μc=0.5,f20=0,结合胞映射方法,可数值仿真得到在状态平面上系统的分岔图和Lyapunov指数图,如图2所示。图中用不同的颜色表示共存的不同吸引子或分岔分支,每个分岔分支及其对应的Lyapunov指数变化曲线用相同颜色表示。

(a)

(b)

(c)

(d) 图2(a)对应的Lyapunov指数图

(e) 图2(b)对应的Lyapunov指数图

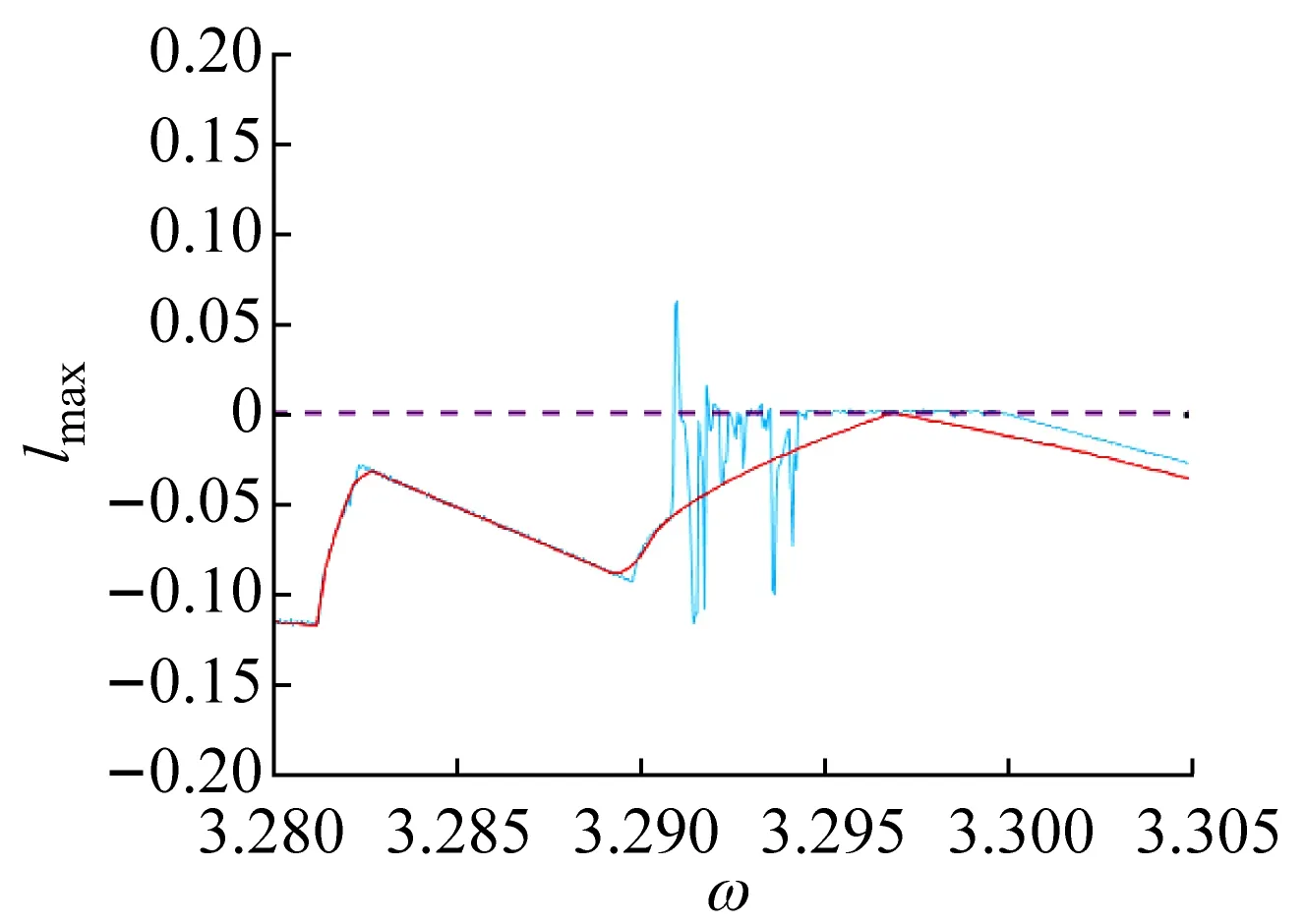
(f) 图2(c)对应的Lyapunov指数图图2 系统的多初值分岔图和Lyapunov指数图Fig.2 Global bifurcation and corresponding Lyapunov exponents with multi-initial points

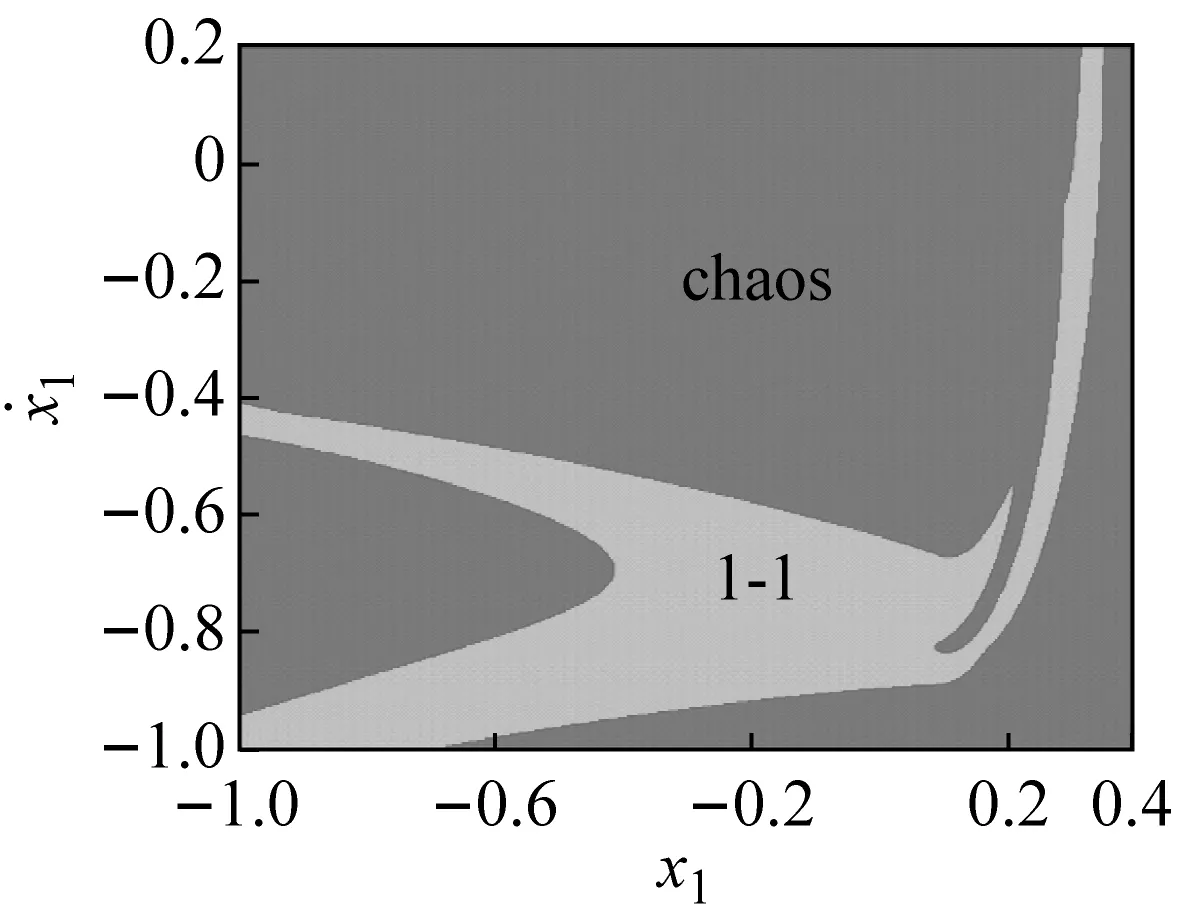
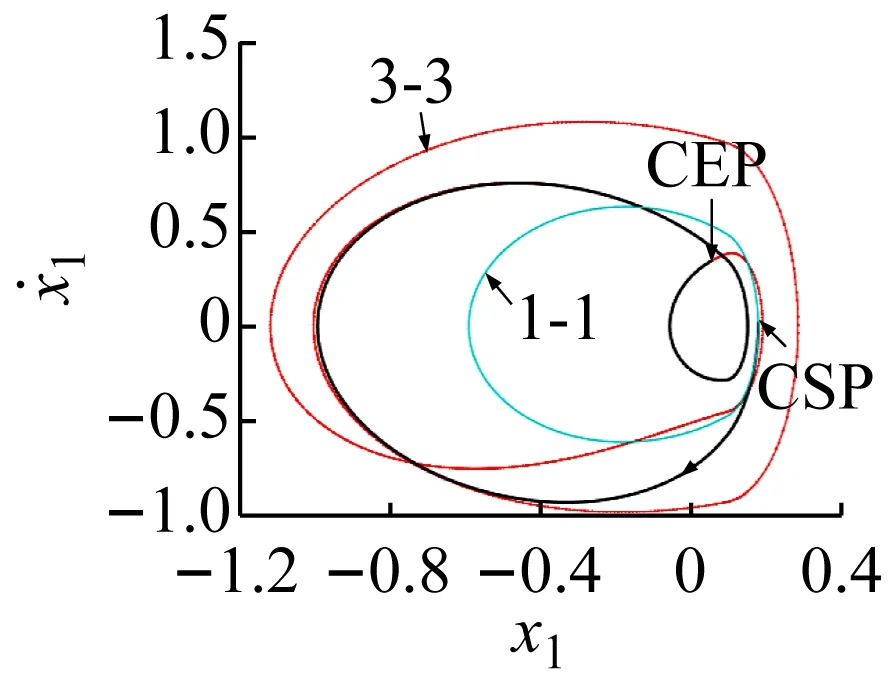
激励频率在ω∈[ω1,ω2]区间内变化时,主要存在1-1与3-3周期运动(吸引域分布如图3(a)所示)、1-1周期运动与混沌运动(吸引域分布如图3(b)所示)以及3-2与2-2周期运动共存等。在此区间内系统的多态共存区之间主要以倍周期分岔进行转迁。在ω=ω2处,3-2周期运动的特征值为:λ1=0.999 923,|λ2,3,4|<1;若ω继续增大,3-2周期运动经鞍结分岔转迁为2-2周期运动,共存现象随即消失。在ω1处,3-3周期运动的特征值为:λ1=1.000 196,|λ2,3,4|<1;若ω减小,3-3周期运动经鞍结分岔转迁为1-1周期运动,共存现象随即消失,系统只存在1-1周期运动。

(a) ω=1.740 3

(b) ω=1.740 5

(c) ω=3.086 0

(d) ω=3.500 7

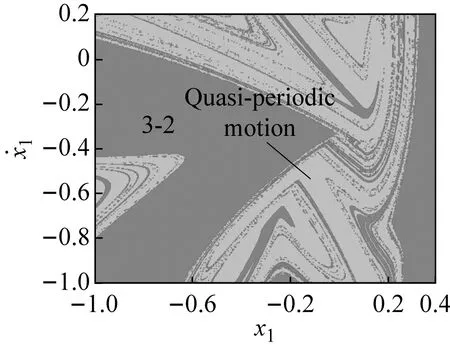
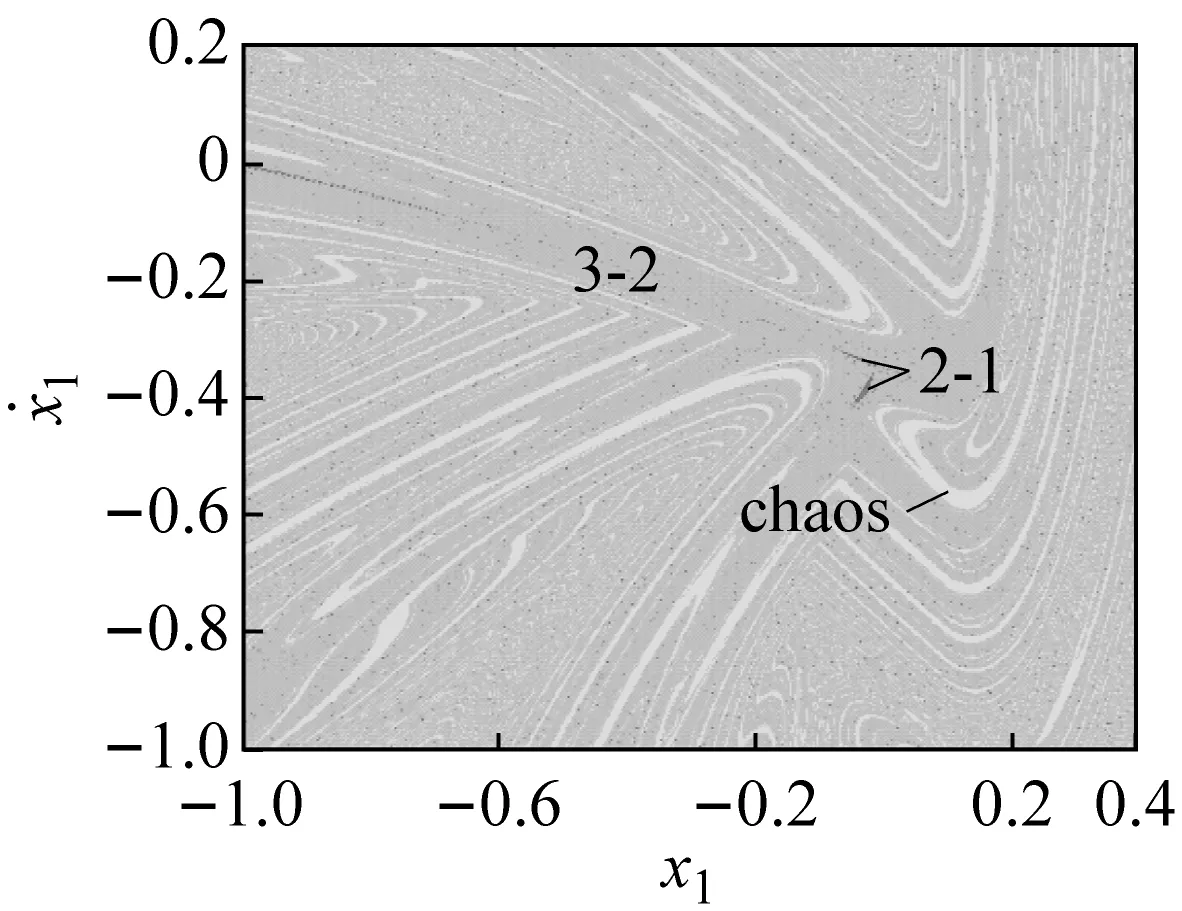
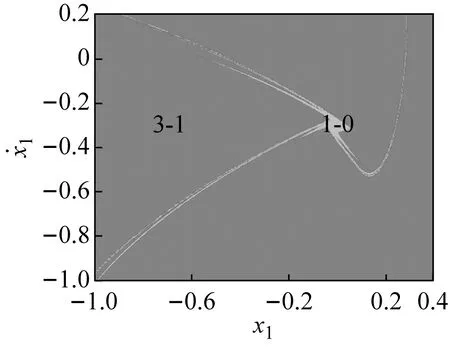
(e) ω=2.298 0图3 吸引域图Fig.3 Basins of attraction of the system

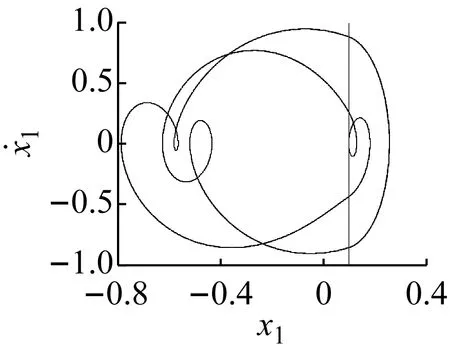
在ω∈[ω3,ω6]区间内,由于对初始状态的敏感性,随着ω的递减,在状态平面上系统的分岔图依次存在三个和两个分支,不同的分支在一些特殊分岔点处会进行转迁或合并,从而造成多态共存区的转迁或消失。在ω=ω4处,若ω减小系统发生擦边分岔,5-3周期运动转迁为7-4周期运动;在ω=ω5处,若ω增大系统发生擦边分岔(擦边相图如图4(a)所示),5-3周期运动转迁为5-2周期运动。在ω4和ω5处擦边分岔未对共存吸引子的个数产生影响,但实现了不同共存区的转迁。在ω=ω3处,7-4周期运动的特征值为

(a) 5-2擦边周期运动

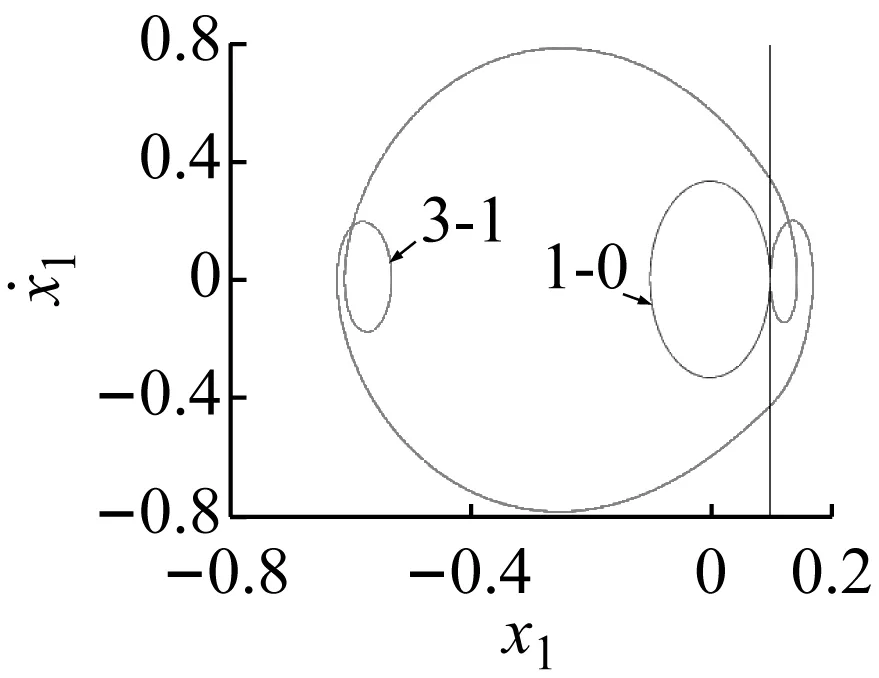
(b) 1-0和3-1擦边周期运动图4 系统擦边运动的相图Fig.4 Phase plane of grazing motion

λ1=1.000 043,|λ2,3,4|<1。

若ω减小,系统将发生鞍结分岔,7-4周期运动转迁为2-1周期运动,从而7-4周期运动所在的分支和2-1周期运动所在的分支合并,系统仅存在2-1周期运动,共存现象随即消失。

在ω=ω6处,5-2周期运动的特征值为

λ1=1.000 065,|λ2,3,4|<1。

若ω增大,系统将发生鞍结分岔,5-2周期运动转迁为混沌运动(从图2(f)所示的Lyapunov指数图可观察到),从而形成混沌运动、2-1和3-2周期运动共存的多态共存区(吸引域分布如图3(c)所示);随着ω的继续增大混沌吸引子与其吸引域边界发生碰撞出现边界激变造成混沌吸引子的消失,之后系统中只保留2-1和3-2周期运动共存。类似的边界激变现象在ω5附近也可以观察到,此处3-2周期运动所在的分支随着边界激变的发生而消失,之后系统中仅存在5-3和2-1周期运动共存。

在ω=ω8处,3-1周期运动的特征值为

λ1=1.000 187,|λ2,3,4|<1。

若ω增大,系统将发生鞍结分岔,3-1周期运动转迁为1-0周期运动,系统吸引子共存现象也随之消失,系统中只保留1-0周期运动(如图2(a)所示)。若ω继续减小,共存的3-1与1-0周期运动(吸引域分布如图3(d)所示)在不同的初始条件下同时发生擦边分岔(擦边相图如图4(b)所示),转迁为3-2与1-1周期运动的多态共存区;随着ω持续减小,1-1周期运动发生Hopf分岔(在ω=3.298处系统的特征值为:|λ1,2|=1.000 788,|λ3,4|<1)转迁为拟周期运动,此时出现拟周期运动与3-2周期运动共存的多态共存区(吸引域分布如图3(e)所示,结合图2(g)所示的状态平面上的Lyapunov指数图可观察并验证);随着ω的继续减小拟周期运动最终进入混沌运动,并且由于边界激变造成混沌吸引子消失,共存现象随即消失。

5.2 系统共存吸引子转迁验证分析

通过上面数值仿真发现,在某些参数条件下,图1所示系统因对初始状态的敏感性,会稳定运行于若干个不同的吸引子上。针对图1所示系统对初始状态的敏感性,以系统共存的某一个吸引子对应的轨道作为目标轨道,而另一吸引子对应的轨道作为被控轨道,通过施加线性反馈控制器,对被控轨道进行力驱动,从而实现吸引子之间的转迁。

取控制参数r=1、u1=5和u2=5,其余参数均为基准参数①,通过Matlab的YALMIP工具包对式(24)、(25)和(26)进行求解,可得为保证控制的稳定性而增加的带有约束条件的参数

P(i,i)>0(i=1,2,3,4),det(P)=5.038 6>0;

λ1=16.899 6>0;λ2=16.394 7>0。

由于上述参数的解都符合假定的约束条件,所以在此控制参数下可以实现系统不同吸引子之间的转迁。

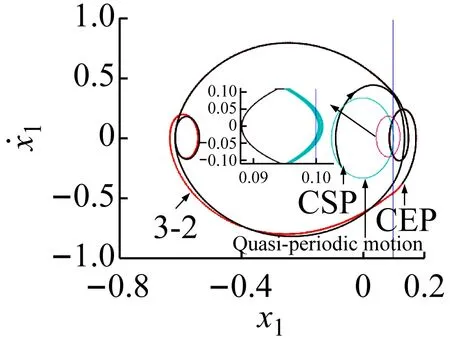
在轨道转迁的过程中,红色轨线代表目标轨道,黑色的轨线代表控制过程,淡蓝色轨道代表被控轨道。当e(t)<ε(e(t)为被控和目标轨道之间的距离,ε为控制精度,设置为0.000 01)时令s(t)=diag(0,0)控制退出,此时系统可成功转迁到目标周期轨道。在不同吸引子转迁的效果图中用以下符号表示控制的不同状态:控制开始位置(control start position, CSP);控制结束位置(control end position, CEP);控制开始时间(control start time, CST)。

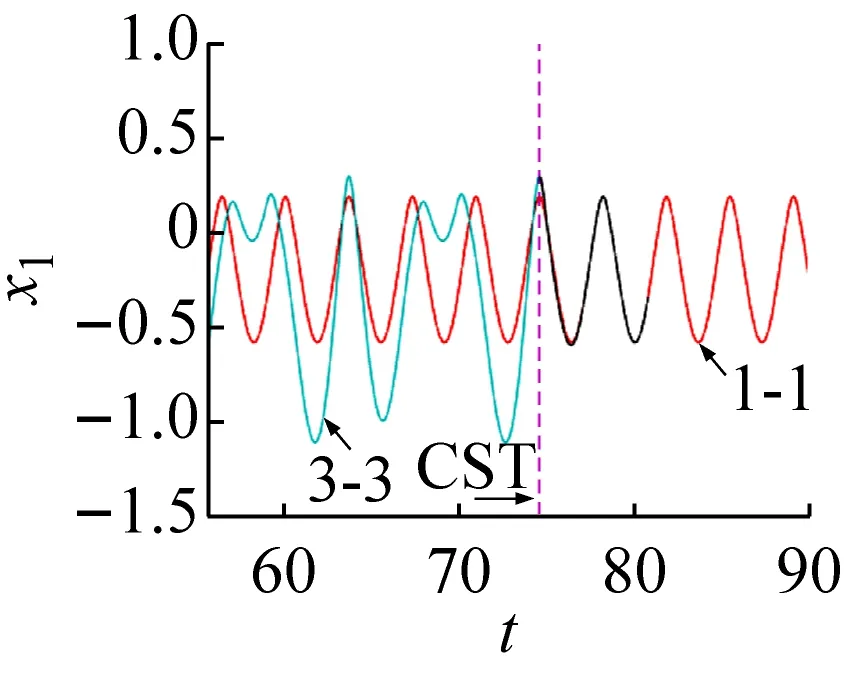
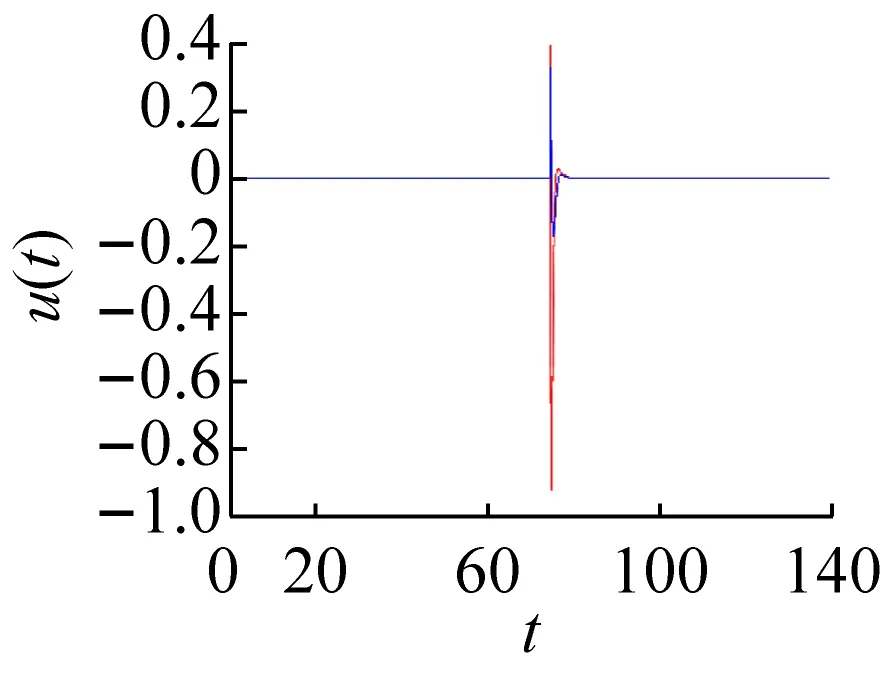
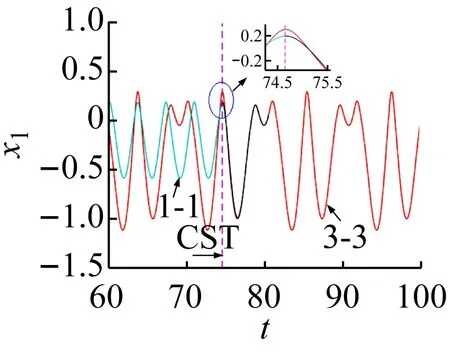
通过数值方法对上述控制方法和参数进行验证。由前面的分析结果可知,在ω=1.740 3时3-3周期运动与1-1周期运动共存。将3-3周期运动轨道作为被控轨道,而1-1周期运动轨道作为目标轨道,在3-3与1-1周期运动轨道之间距离最小时施加控制,如图5所示。图5(a)、(b)、(c)和(d)分别为将3-3周期运动转迁至1-1周期运动时的相图和位移、反馈控制力和控制误差的时间历程图。结合图5(d)可看出,当控制未施加时系统被控轨道和目标轨道之间的距离变化具有周期性,被控系统会稳定运行在振幅较大的3-3周期运动上。结合图5(a)、(b)、(c)可看出,当施加控制后,被控轨道在线性反馈控制力的作用下快速向目标轨道迁移,且反馈输入力和控制误差会随着被控轨道和目标轨道之间距离的减小而逐渐减小;在控制施加前和控制完成后,线性反馈控制力都为零,说明此种方法不需要能量的持续输入。在实际系统中,还需考虑是否限制控制器输入的上限值,若控制器输入比较大时,直接施加如此大的一个反馈控制力可能会对系统产生不利的影响或者损坏控制器。

(a) 相轨迹转迁过程

(b) 位移转迁过程

(c) 反馈控制力的时间历程图

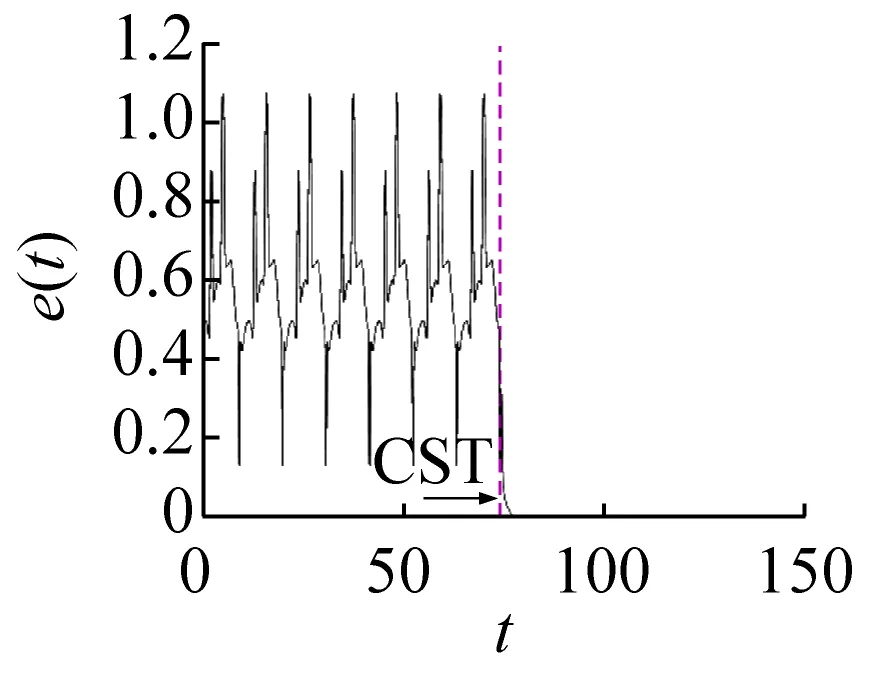
(d) 控制误差时间历程图图5 3-3周期运动转迁至1-1周期运动的效果图Fig.5 The effect chart of 3-3 periodic motion migrating to 1-1 periodic motion

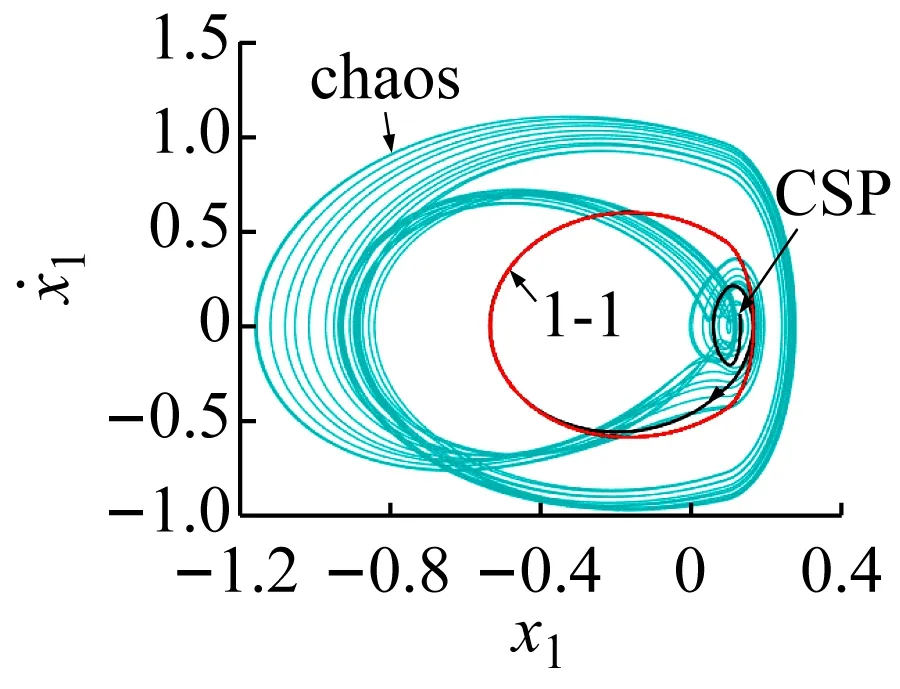
将1-1周期运动转迁至3-3周期运动的过程如图6所示;将混沌运动转迁至1-1周期运动过程如图7所示;将拟周期运动转迁至3-2周期运动的过程如图8所示;将1-0周期运动转迁至3-1周期运动的过程如图9所示。

(a) 相轨迹转迁过程

(b) 位移转迁过程图6 1-1周期运动转迁至3-3周期运动的效果图Fig.6 The effect chart of 1-1 periodic motion migrating to 3-3 periodic motion

(a) 相轨迹转迁过程

(b) 位移转迁过程图7 混沌运动转迁至1-1周期运动的效果图Fig.7 The effect chart of chaotic motion migrating to 1-1 periodic motion

(a) 相轨迹转迁过程

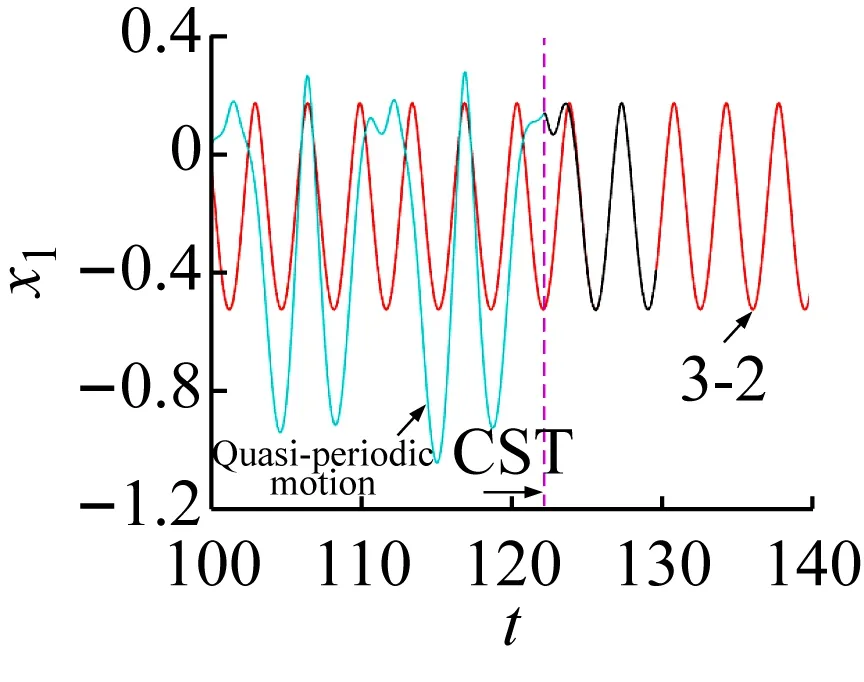
(b) 位移转迁过程图8 拟周期运动转迁至3-2周期运动的效果图Fig.8 The effect chart of quasi-periodic motion migrating to 3-2 periodic motion

(a) 相轨迹转迁过程

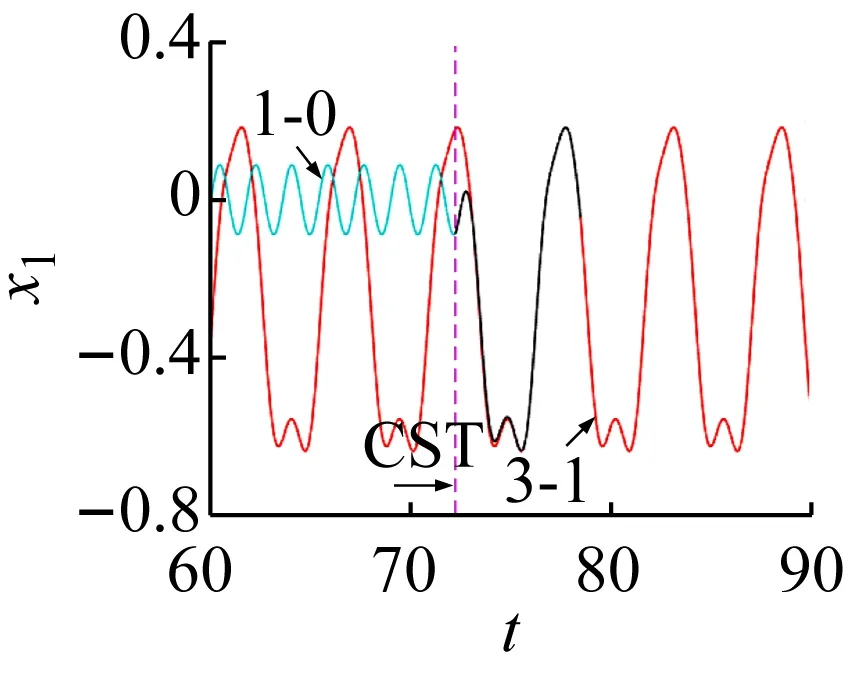
(b) 位移转迁过程图9 1-0转迁至3-1周期运动的效果图Fig.9 The effect chart of 1-0 periodic motion migrating to 3-1 periodic motion

由上述仿真结果可见,利用本文方法能够很好地实现对系统共存吸引子之间的相互转迁。上述周期运动之间的相互转迁,不仅可调整系统与约束面的关系,使系统按照不同的使用要求工作;当激励频率正向或反向迭代时还可控制各种分岔的发生;将混沌运动转迁周期运动,可实现对混沌运动的控制。

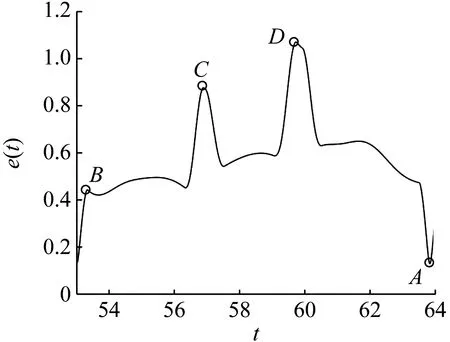
在控制过程中,控制开始状态的设置需考虑目标轨道和被控轨道之间距离对控制效果的影响,当目标轨道和被控轨道之间距离较大时施加控制,则在控制初始时刻系统的状态会出现较大的跳动,反馈控制力较大,且控制过程持续时间较长;而当目标轨道和被控轨道之间距离较小时施加控制,则在控制初始时刻系统状态的过渡会比较平稳,反馈控制力最小,且控制过程持续时间也最短。以1-1周期运动转迁至3-3周期运动为例进行验证。选取三倍激励周期内被控轨道和目标轨道之间距离的局部极大值点(B和C)以及全局的最大值点(D)和最小值点(A)(如图10(a)所示)分别为控制开始状态进行控制。图10(b)为反馈控制力的时间历程图,表1为不同控制开始状态下反馈控制力的最大值和控制过程持续时间。从图10(b)和表1可看出,不同的控制开始状态需要的反馈控制力和控制过程经历时间不同,当e(t)最大时需要的控制力最大,控制过程持续时间也最长;而e(t)最小时需要的控制力最小,控制过程持续时间也最短;所以在此类系统的共存吸引子转迁控制过程中应选择被控轨道和目标轨道之间距离最小时施加控制。

(a) 控制误差的时间历程图

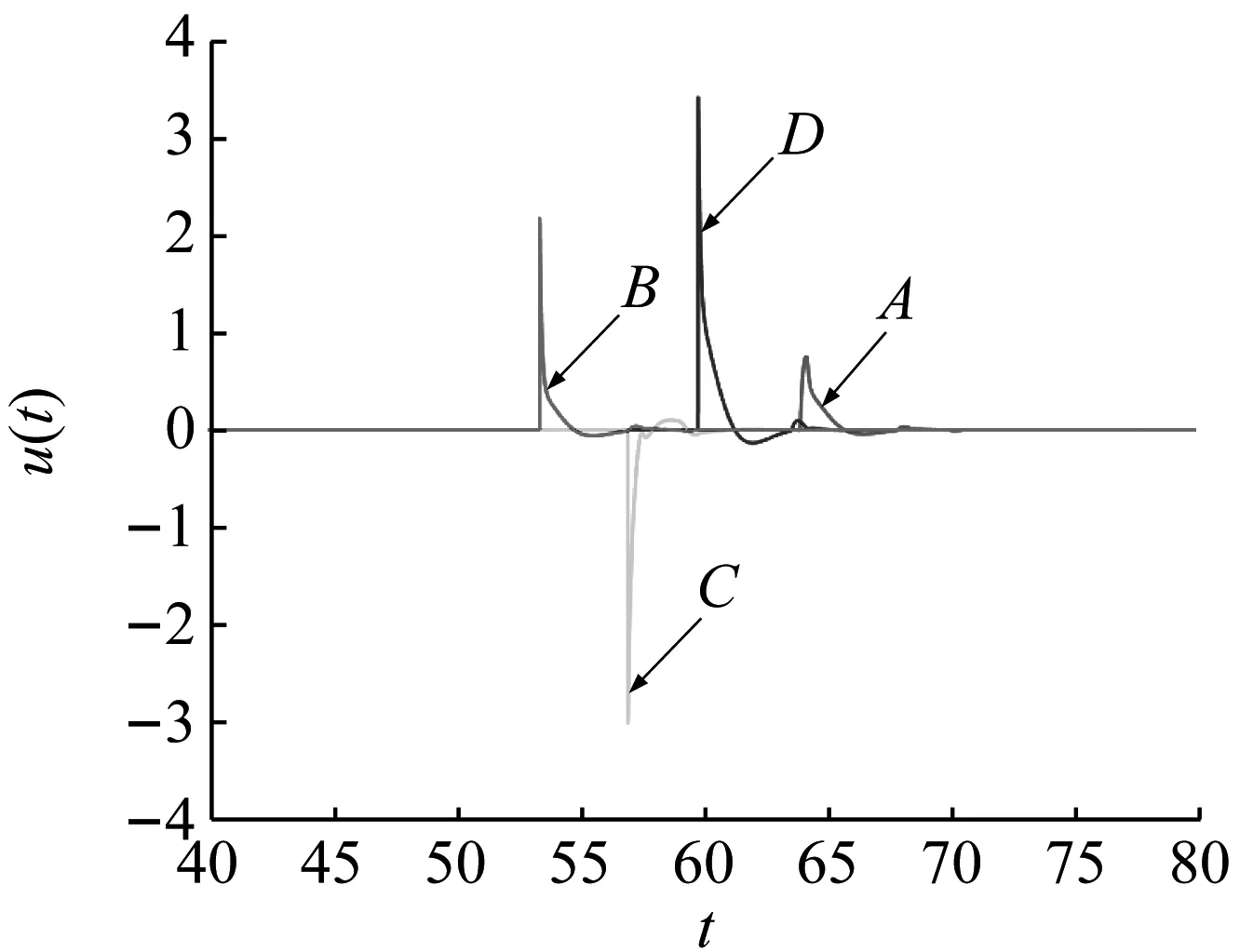
(b) 反馈控制力的时间历程图图10 不同控制开始状态对反馈控制力的影响Fig.10 The effect of different control starting positions on feedback control force

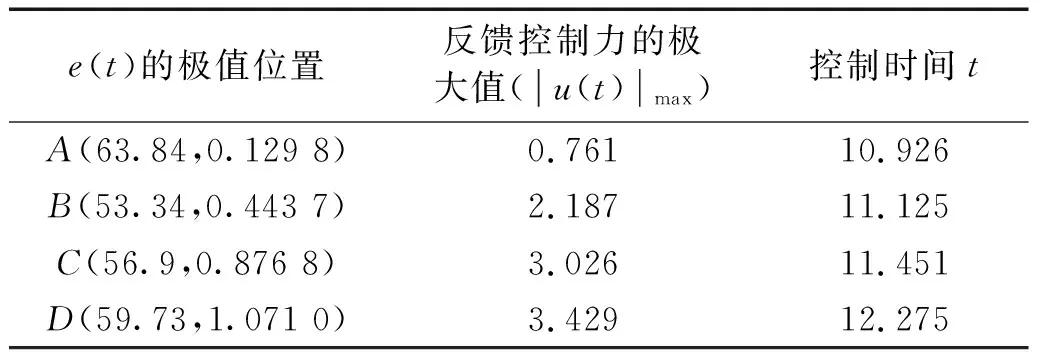
表1 不同控制开始状态下的控制性能Tab.1 Control performance under different control start states

6 结 论

针对两自由度含间隙分段线性系统的吸引子共存现象,利用线性反馈控制对共存吸引子实现了相互转迁,可以得到如下结论:

(1) 相邻吸引子之间的相互转迁由系统参数和初始状态共同决定;鞍结分岔是引起此类系统产生吸引子共存的主要原因,倍周期分岔和擦边分岔不会对共存吸引子的吸引域结构产生影响,但能实现不同共存区的转迁,边界激变是混沌吸引子及其吸引域突然消失的主要原因。

(2) 施加线性反馈控制器后,通过构造二次Lyapunov函数,利用LMI理论并结合系统分段线性的特点,可将被控系统的向量场信息通过S-procedure考虑进稳定性条件,从而将线性反馈控制的稳定性和反馈增益矩阵的选取问题转化为LMI描述,这样可解决线性反馈控制在实现分段线性系统共存吸引子转迁中的稳定性分析及反馈增益矩阵选取问题。

(3) 在此类系统共存吸引子转迁控制过程中,应选择被控轨道和目标轨道之间距离最小时开始施加控制。吸引子之间的相互转迁一方面可使系统工作在理想的周期运动上;另一方面可控制混沌运动的发生,达到提高系统稳定性及减振性能的目的。