新月形薄覆冰导线气动力特性数值模拟研究
2023-10-18肖志斌楼文娟黄铭枫2张跃龙
林 巍, 肖志斌, 楼文娟, 黄铭枫2,, 张跃龙
(1. 浙江大学 建筑设计研究院有限公司, 杭州 310027; 2. 浙江大学 平衡建筑研究中心, 杭州 310027;3. 浙江大学 结构工程研究所, 杭州 310058)
在特殊的气候条件下,输电导线可能会在其迎风面结冰,从而改变其截面形状使受力变得复杂。在一定的风速和攻角条件下,导线容易产生舞动。舞动是一种低频率(0.1~3 Hz)、大振幅(导线直径的5倍~300倍)的自激振动。输电线路的覆冰和积雪以及由此衍生的导线舞动已经严重威胁着电力及通信网络的安全运行。
导线舞动的机理十分复杂,目前国际上比较公认的是Den Hartog[1]横向舞动机理和Nigol[2]扭转舞动机理。无论采用何种舞动机理,覆冰输电导线的气动力特性是导线舞动分析的重要参数。因此,研究覆冰输电导线的气动力特性对输电导线舞动的研究及防治具有重要的意义[3]。
Masataka[4]对输电线路124次舞动过程进行了实际观测,归纳了不同覆冰形状下对应的舞动次数,如表1所示,表中D为导线直径。可以看出,在实际的舞动中导线新月形覆冰情况占据较大比重;对于新月形覆冰而言,0~0.5D的薄覆冰情况下导线舞动次数达总次数的92%。说明新月形薄覆冰对导线舞动起着关键作用。
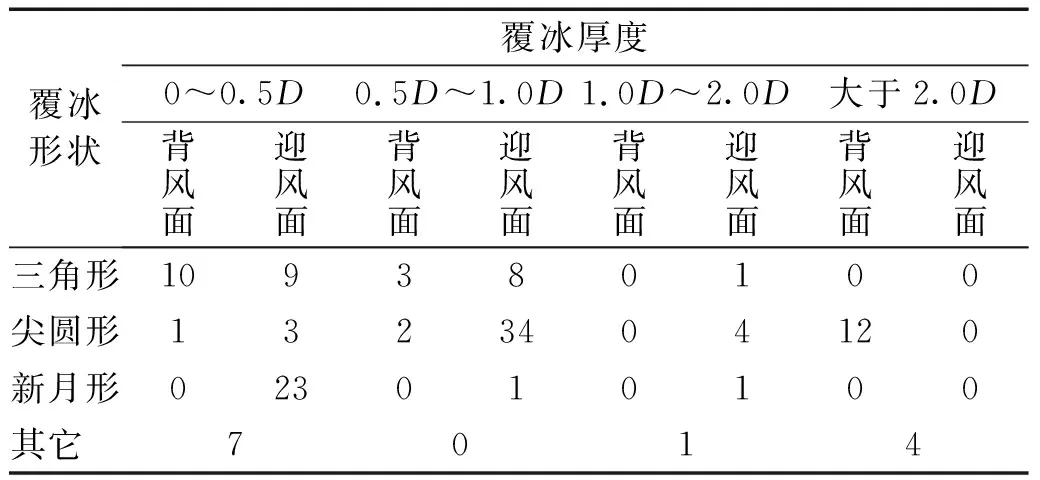
表1 不同覆冰类型对应的舞动次数Tab.1 Number of galloping corresponding to different ice accretion types
风洞试验和数值模拟是获取覆冰导线气动力特性的主要手段。Nigol在均匀流场风洞中测量了新月型覆冰导线的空气动力参数;Chadha等[5]在风洞中测量了覆冰导线的三分力系数,考虑了湍流度对气动力的影响; Chabart等[6]在对新月形覆冰截面进行气动力特性试验,得到了新月形覆冰导线的三分力系数及其拟合曲线;Ishihara[7]对 3种不同覆冰厚度的新月形覆冰的单导线及四分裂导线进行气动力特性试验,给出了均匀流场下的气动力特性;张宏雁等[8]通过试验研究新月形和扇形覆冰导线在不同风速下的气动力特性;顾明等[9]通过节段模型高频天平测力风洞试验, 计算了准椭圆形和扇形两种代表性覆冰导线的气动力系数均值、均方根值;马文勇等[10]也开展了准椭圆覆冰导线的气动特性试验研究。然而,由于覆冰的多样性,目前有关覆冰导线的气动力参数仍缺乏系统全面的数据。
姚育成[11]在高雷诺数下,在二维空间对不同冰厚的新月形覆冰导线的气动力特性进行了数值模拟;吕翼等[12]通过对新月形和扇形覆冰的单导线、三分裂导线的气动力特性进行了二维数值模拟;李新民等[13]对几种典型覆冰导线的气动力特性进行了二维数值模拟;韦远武等[14]结合重叠网格技术实现覆冰导线静态与动态气动力模拟。李彭举等[15]对新月形覆冰八分裂导线的气动力特性进行了二维数值模拟。但已有的相关数值模拟研究大多把流域简化为二维流场,其结果只能定性的反映气动力随攻角的变化趋势,具体数值与试验结果还有较大的差异。
圆柱绕流是空气动力学中经典的绕流问题,国内外学者对此进行了大量的试验研究和数值计算,已有结果包含的风速、风压结果信息丰富,相对较为成熟。Breue[16]采用大涡模拟(LES)方法对孤立圆柱绕流问题(Re=140 000)进行了三维的数值模拟,通过不同离散格式和亚格子模型的比较,表明选择合适的近壁处理和亚格子模型能和试验结果吻合较好。 Kravchenkoa[17]采用动力亚格子模型对亚临界状态下圆柱绕流问题进行了三维数值模拟。输电导线由于其直径较小,其雷诺数基本处于亚临界范围,本文首先通过对圆柱绕流问题的LES数值模拟,考察近壁面网格对风速、风压等结果的影响, 并同时验证了采用k-ωSST 湍流模型的可行性。在此基础上对新月形覆冰单导线的气动力特性进行数值模拟,并与风洞试验结果对比。为今后进行其他覆冰形状气动力数值计算提供参考。
1 试验概况
导线覆冰情况极其复杂,具有很强的随机性。 Masataka对124次舞动观测中的覆冰形状进行了归类,发现在实际舞动的观测中新月形覆冰占有很大的比重。新月形是输电导线主要的覆冰形式且截面形状易于量化,常作为气动力特性的研究对象。本文试验裸导线直径采用LGJ-400/35(直径26.8 mm),覆冰厚度为0.25D,D为裸导线直径。试验在浙江大学边界层风洞(ZD-1)中完成,试验来流风速取10 m/s,由截面的对称性,试验风攻角范围取0°~180°,风向角间隔为5°。测力采用高频测力天平,水平力量程为20 N,扭矩量程为 4 N·m,天平最高测力频率1 000 Hz。图2为模型的风洞试验照片,试验模型和设备详见文献[18]。
覆冰导线的气动力可表示为升力FL、阻力FD和扭矩M,如图1所示。并将气动力无量纲化可得

图1 气动三分力方向及风向角定义Fig.1 Definition of aerodynamic force direction and wind angle
(1)
式中:CL、CD、CM分别为覆冰导线的升力系数、阻力系数和扭转系数;U为试验风速;ρ为试验时空气密度;D为裸导线的直径;l为模型的有效长度。
2 圆柱绕流数值模拟
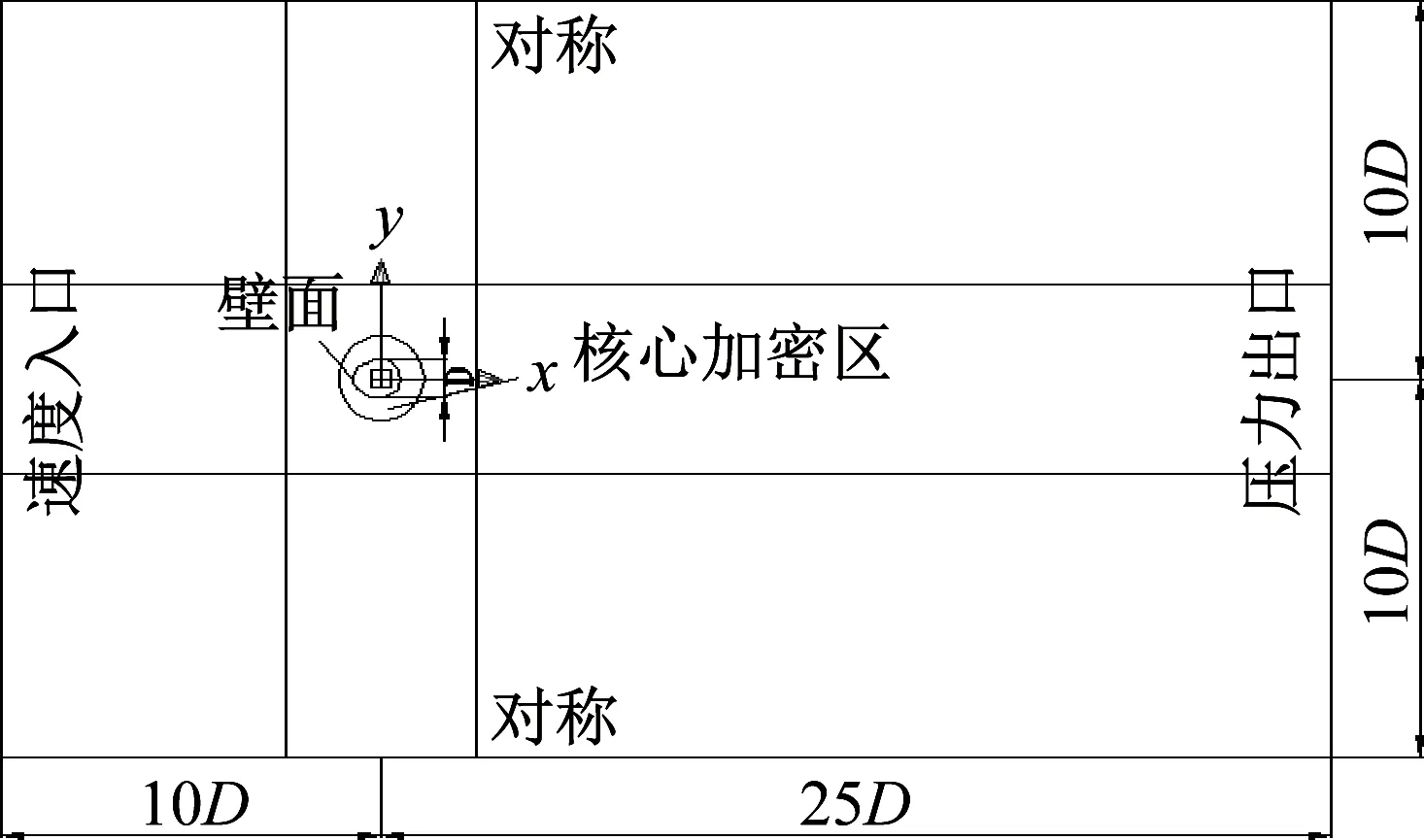
为验证数值计算模型,本文将以圆柱为研究对象,分别进行二维和三维 LES 非定常绕流计算,并验证采用k-ωSST 湍流模型的可行性。为与以往圆柱试验文献结果对比,雷诺数Re取3 900。计算流域及边界条件,如图3所示。流场区域足够大,使尾流及涡脱落能充分发展。

图2 新月形单导线模型试验照片Fig.2 Crescent single conductor model test

图3 圆柱绕流计算流域及边界条件Fig.3 Calculation of basin and boundary conditions for flow around a cylinder
2.1 圆柱绕流计算基本参数
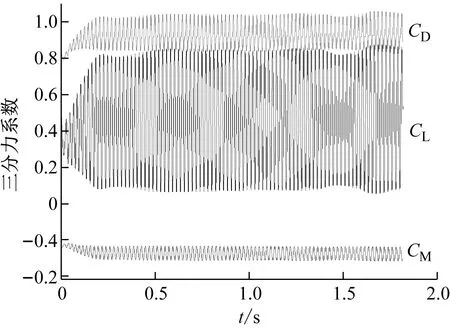
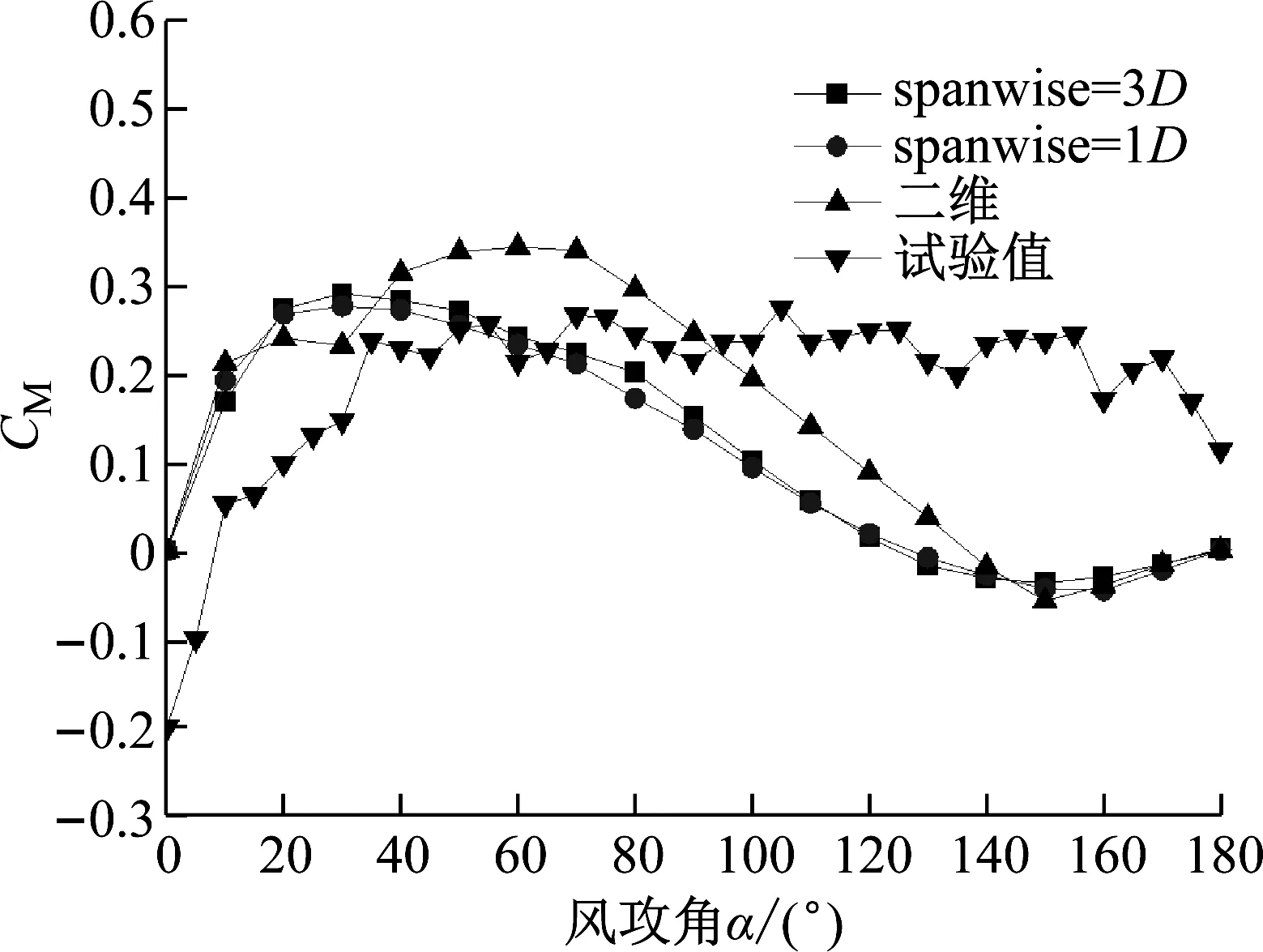
圆柱直径D=2 cm,将整个流域划分为9个子域,计算域网格划分采用非均匀的结构网格,其中子域5为核心加密区,远离圆柱表面的网格逐渐扩散。三维计算模型展向长度分别取3D和1D。为考察近壁面网格对计算结果的影响,综合考虑y+值,x-y平面内网格采用了两种不同密度的网格划分方式:(1) mesh1:近壁面第一层网格尺度为0.003D,对应壁面y+<1,加密区网格以1.05的系数向外扩散,具体网格划分见图4(a)。(2) mesh2:近壁面第一层网格尺度为0.01D,对应壁面1 (a) mesh1(优质的) (b) mesh2(粗糙的)图4 圆柱绕流网格平面图Fig.4 Grid plan of flow around a cylinder 数值计算的速度入口和初始条件如下:圆柱表面为无滑移边界(u=v=0);速度入口为2.925 m/s均匀风速;上下边界为对称边界(u=U,v=0);出口条件为压力出口。 在非定常计算前,先采用基于RANS的Realizablek-ω湍流模型进行圆柱绕流定常计算,使其流场达到稳定的状态,并以此作为非定常绕流计算的初始条件,这样可以使圆柱尾流区较早进入充分发展阶段。非稳态计算时间步长取0.000 5 s。 为考察亚格子模型和近壁面网格对数值结果的影响,分别选用标准Smagorinsky模型和Dynamic-Smagorinsky模型进行比较。通过计算可以发现,三维大涡模拟非定常绕流非常耗时。如果在现在普通8核微机上计算,要获得一个统计意义上稳定的时程,计算时长往往在100 h以上甚至更长。对覆冰导线来说,需要计算不同风攻角下的气动力系数,这样长的计算时间是无法接受的。为此,同时选择k-ωSST湍流模型进行比较。主要计算工况如表2所示。 表2 圆柱绕流计算工况表Tab.2 Calculation condition of flow around a cylinder 对表2中所有工况进行圆柱绕流CFD非定常计算,并将本文计算结果与以往风洞试验结果[19-21]和数值模拟结果进行对比分析,主要针对平均风压系数、平均速度场及斯托劳哈数(St)等。 定义测点的风压系数如下 (2) 式中:Pi为测点的压力;ρ为空气密度;U∞为来流风速。 图5为本文LES数值模拟所得的平均风压系数与以往风洞试验结果的比较,图中“expRe=3 900”表示Re=3 900时文献[19]中的试验结果。在平均风压系数方面:① 如图5(a)所示,基于两种网格及不同亚格子模型下,二维LES计算结果与风洞试验结果差别都较大。主要在圆柱侧面的分离区和背后的尾流区差别十分严重。几种工况下结果差别不大;② 由图5(b)、(c)可见,表面的压力系数在正对来流处为1,随着向周围扩展,压力系数值减小,达到最小值后很快增大到一个较为稳定的值并在圆柱背后形成平坦的稳态压力分布,变化趋势与试验结果吻合。mesh1网格下计算结果优于mesh2网格,Dynamic-Smagorinsky亚格子模型计算结果优于Smagorinsky下计算结果。展向长度取1倍特征长度时已显示很好的计算精度,展向长度取3倍特征长度对计算精度改善不明显。 (a) 二维计算结果 (b) 展向长度1D (c) 展向长度3D图5 平均风压系数比较Fig.5 Comparison of average wind pressure coefficient LES计算所得圆柱流向(x)中心线(y=0,z=H/2)的平均速度场和横风向(y)近壁区(x/D=1.54,z=H/2)脉动速度场的比较结果如图6 ~图8所示,U0为入口来流速度,u′,v′分别为x,y方向的脉动速度。从风压比较图中知,二维计算结果与试验结果差别较大,因此对二维速度场计算结果此处不再列出。 (a) 展向长度1D (b) 展向长度3D图6 x流向平均速度比较Fig.6 Comparison of mean velocity in x direction (a) 展向长度1D (b) 展向长度3D图7 x向脉动速度比较(x/D=1.54)Fig.7 Comparison of pulsating velocity in x direction(x/D=1.54) (a) 展向长度1D (b) 展向长度3D图8 y向脉动速度比较(x/D=1.54)Fig.8 Comparison of pulsating velocity in y direction(x/D=1.54) 由图6可知,对圆柱流向中心线平均风速来说:① 在圆柱尾流近壁区(图中x/D<1.0区域),不同工况下的计算结果与风洞试验结果均比较吻合;② 在圆柱远离壁面尾流区(图中x/D>1.0区域),不同工况下的计算结果与风洞试验结果吻合度不尽相同。基于mesh1网格的计算结果优于mesh2网格的结果;亚格子模型对计算精度的影响较大。展向长度1D与3D时所得计算结果无明显差别。 由图7可知,对于圆柱x/D=1.54处x向脉动风速来说,除1D_mesh2_dsma工况外,其他各工况下计算结果差别不大,与风洞试验结果吻合较好。 由图8可知,对于圆柱x/D=1.54处y向脉动风速来说,在圆柱特征长度以外(图中y/D<-0.5和y/D>-0.5),各工况所得计算结果无明显差别,与风洞试验结果吻合较好。但对圆柱特征长度范围内(图中-0.5 各工况下圆柱气动力系数统计值与风洞试验和以往数值模拟的比较如表3所示。表中St为斯托劳哈数,定义为 表3 圆柱绕流气动力统计值Tab.3 Aerodynamic statistics of cylinder flow (3) 式中,f为涡脱频率,Hz。升力系数和阻力系数均用来流平均风速无量纲化。CD,mean表示阻力系数均值。表中Cp,back为圆柱尾部点处风压系数。 如图9所示是计算时间100D/U0(约22个涡脱周期) 后1D_mesh1_dsma工况和k-ωSST工况下升、阻力系数的时程曲线。由时程曲线上可知,除大涡的周期脱落外还包括小涡的脱落(在图中表现为高频脉动部分),这是与k-ωSST、k-ω等时均湍流模型结果只含有低频部分不同之处。因此,LES模型需要更长的计算时间来获得如表3中具有统计意义的时均量。 (b) SST模型图9 圆柱升、阻力系数时程Fig.9 Lift and drag coefficient time history of the cylinder 通过对风压、速度、气动力及尾流涡脱频率等的比较,对于圆柱绕流来说,近壁面网格的疏密对LES计算结果有较大影响,近壁网格越密计算结果越精确。Dynamic-Smagorinsky亚格子模型因为CS不再固定具有更好的精度;对平均气动力而言,二维网格过高的估计了圆柱的平均阻力系数,这与图5(a)中圆柱负压区风压系数数值偏小有关;但展向长度取1倍特征长度的三维模型所得计算结果已经足够精确。k-ωSST模型对此类钝体绕流问题也具有较高的精度,考虑到计算效率问题,遇到工况较多时,采用k-ωSST湍流模型是可行的。 覆冰导线截面尺寸同风洞试验,覆冰0.25D。为再次考察展向长度对导线气动力的影响,对比二维模型与三维模型的区别。计算时取二维模型和展向长度分别为1倍导线直径(1D)和3倍导线直径(3D)的三维模型。计算域大小取为35D×20D×1D,如图10(a)所示。采用区域分块非均匀结构化网格,附面层网格与外部网格间为加密的非结构网格过渡区,展向划分为10份。为保证壁面附近y+≈1,最小网格尺寸为0.000 8D。风攻角定义如图1所示,0°风攻角下网格划分平面图如图10(b)、(c)所示,总网格数约23万。 (a) 计算域及边界条件 (c) 局部网格图10 边界条件、计算域和离散网格平面示意图Fig.10 Schematic diagram of boundary conditions, calculation basin and grid plan 采用速度入口边界条件,来流风速为10 m/s,湍流度为5%;出口为压力出口边界条件;y向和z向侧面为对称边界条件;导线表面为无滑移壁面,如图10(a)所示。在进行非稳态计算前,先进行稳态计算,然后将稳态计算的流场作为k-ωSST非定常计算的初始流场。非稳态时间步长取0.000 5 s。 覆冰导线的三分力系数定义如前文所述,取计算所得时程稳定后的若干个周期的平均值,得到覆冰导线平均三分力系数。20°攻角下模型展向长度取3D的气动三分力系数时程,如图11所示。 图11 20°攻角下气动三分力系数时程Fig.11 Time history of aerodynamic three component force coefficient at 20 °angle of attack 图12给出了新月形覆冰单导线气动三分力系数数值模拟与文献[18]风洞试验结果的对比。 图12 覆冰单导线气动三分力系数计算结果Fig.12 Results of aerodynamic three component coefficient of iced single conductor 由图12可以看出,三维模型计算所得的阻力系数的数值模拟结果与风洞试验结果在各攻角下符合较好。升力系数曲线在两个尖峰对应的攻角处存在一定的误差,展向长度3D优于1D结果,其他攻角下与试验结果较为一致。阻力系数曲线展向长度取3D与1D相差不大。扭转系数的数值模拟结果与风洞试验结果存在较大差异。主要原因在于,该薄覆冰模型的扭矩量级很小,小量级下本次测力天平已不能精确反应扭转系数的大小,因此,随着攻角的变化,测力结果已不能反应扭转系数值的变化。而数值模拟恰好能弥补这一缺点。 总的来说,三维计算模型的计算结果与测力结果是比较一致的,虽然个别攻角下存在一定误差,但计算结果仍能较好的反应气动力的随攻角的变化。二维计算模型与试验结果差别较大,采用三维模型是必要的。展向长度取3D略优于取1D的计算结果。 展向长度取3D时计算的平均风压分布结果如图13所示。由图可知,风压分布对风攻角的变化非常敏感,当α=0°时,覆冰导线截面上面对称,表面风压也呈对称分布,升力系数平均值等于零;当α=10°和α=20°时,上下表面风压不再对称,上表面负压大于下表面,这也是升力系数大于零的原因。 (a) α=0° (b) α=10° (c) α=20° (d) 平均风压系数分布图13 单导线表面平均风压分布结果Fig.13 Average wind pressure distribution on the surface of single conductor 本文通过CFD数值模拟方法对雷诺数为3 900的经典圆柱绕流问题进行了非定常计算,通过不同计算工况下平均风压、平均风速、脉动风速、斯托劳哈数(St)等参数与以往试验结果的对比,研究了近壁面网格及展向长度对结果的影响。在此基础上,通过k-ωSST湍流模型计算了新月形薄覆冰单导线二维和三维网格模型的气动三分力系数。 (1) 近壁面网格的疏密对风压系数、气动力和流场的计算结果有较大影响,近壁网格越密计算结果越精确。通常要求壁面y+值在1左右。 (2) 圆柱绕流计算表明,一个完整的大涡脱落周期内将出现一次升力的最大值和两次阻力的最大值。从精度上讲,采用壁面y+<1的网格并配合使用Dynamic-Smagorinsky亚格子模型可以得到很好的钝体绕流大涡模拟计算结果,但若仅以平均气动力为目标,采用k-ωSST计算是可行且高效的。 (3) 薄覆冰单导线的计算结果与试验结果对比表明,二维与三维模型存在较大区别,采用三维计算模型是必要的。展向长度取3倍导线直径能取得较好的计算结果。

2.2 圆柱绕流计算工况
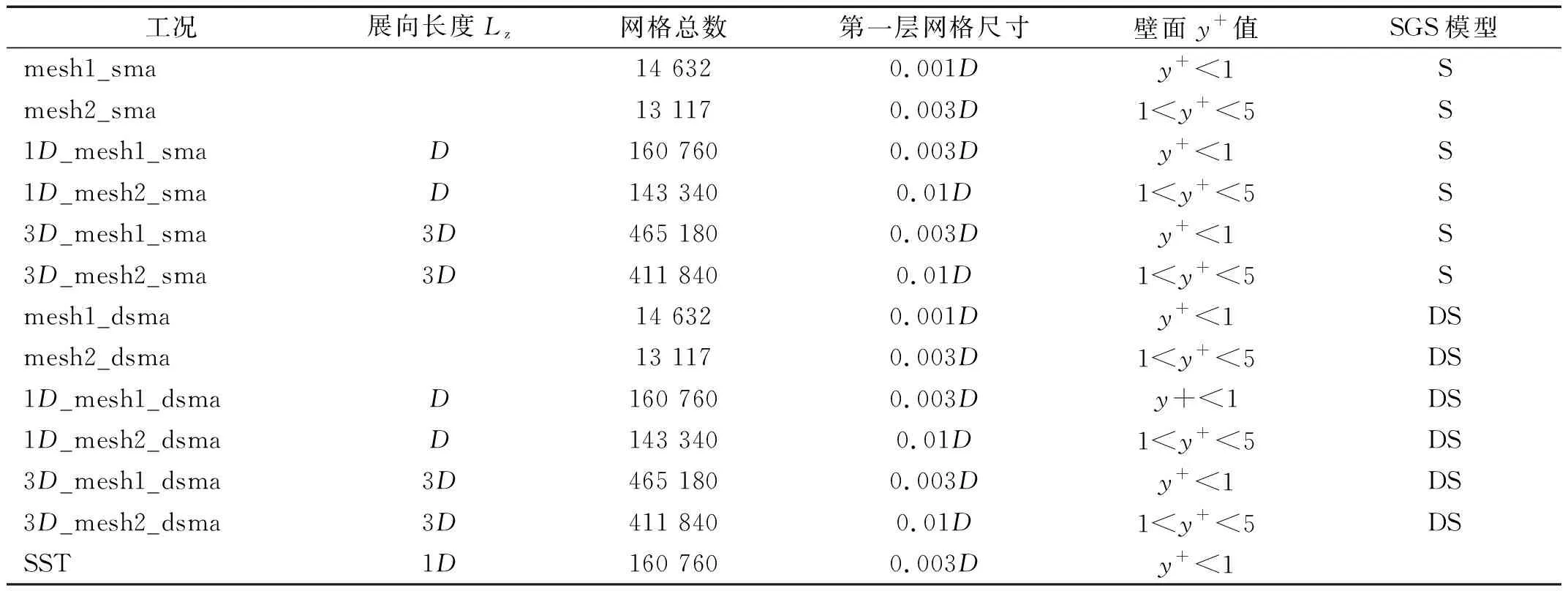
2.3 圆柱绕流计算结果



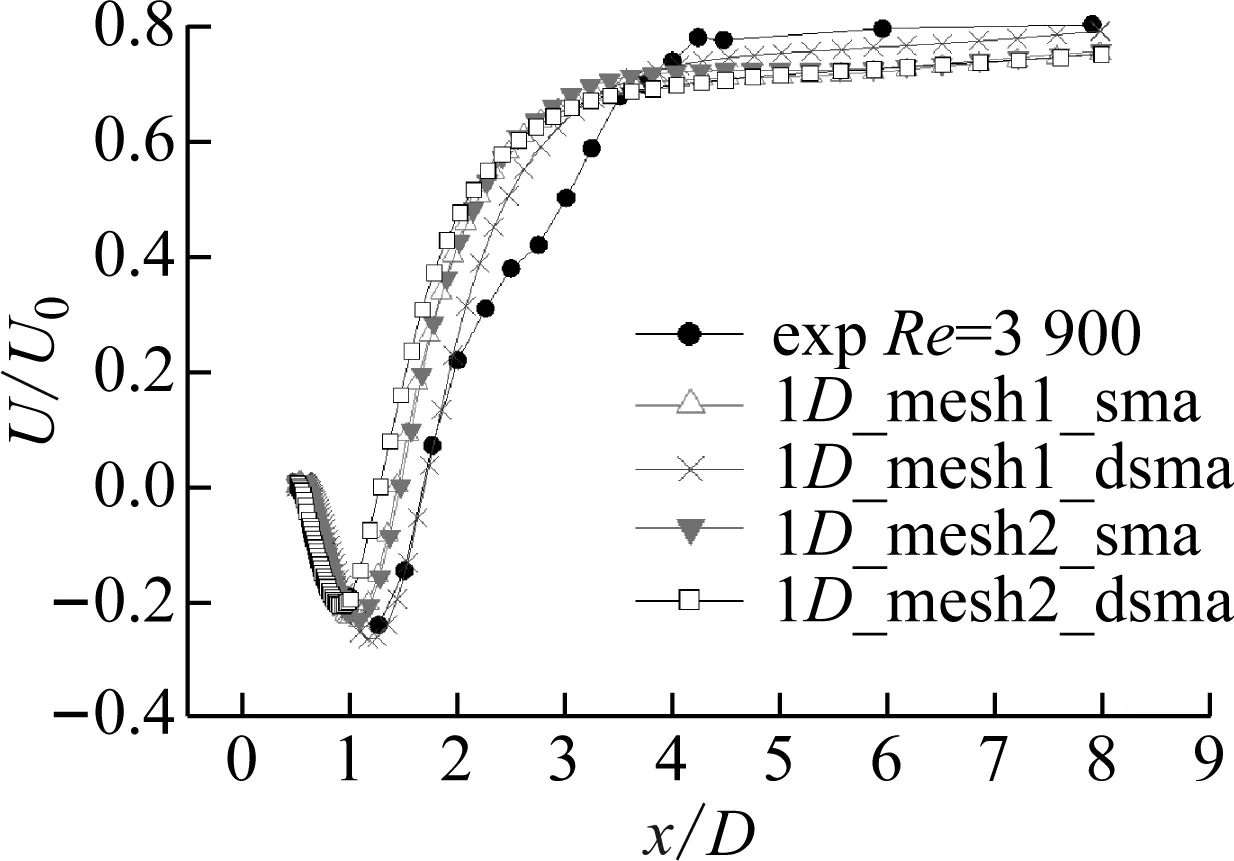


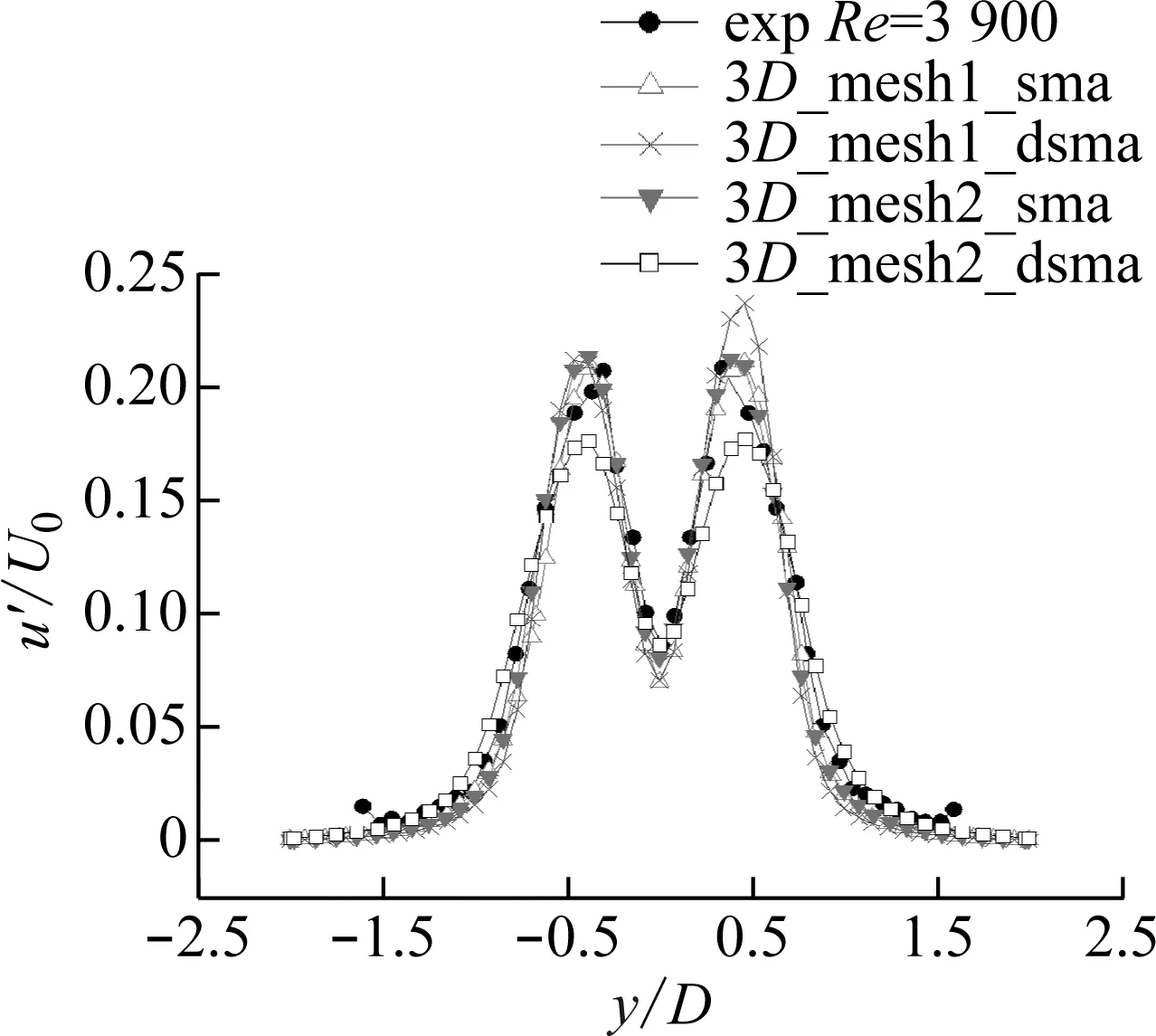
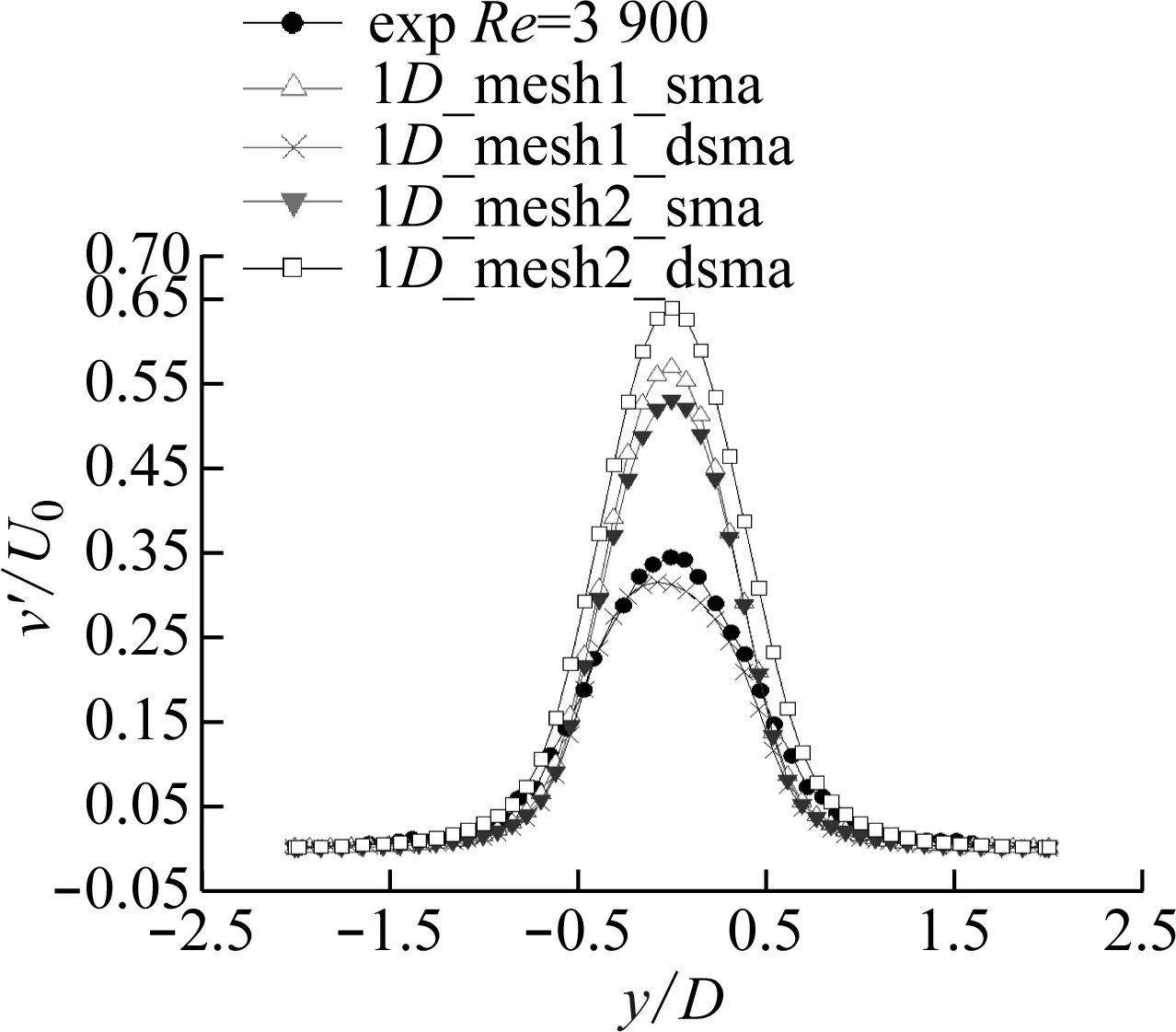

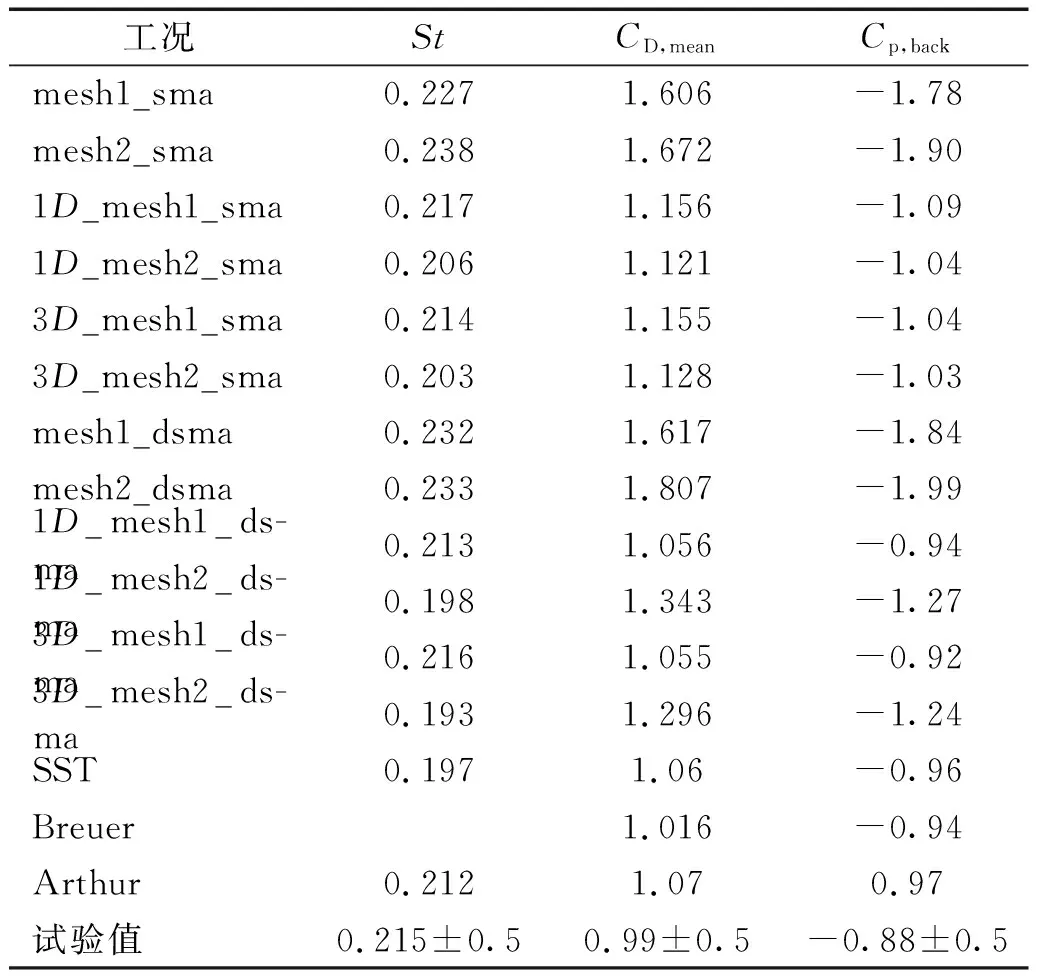
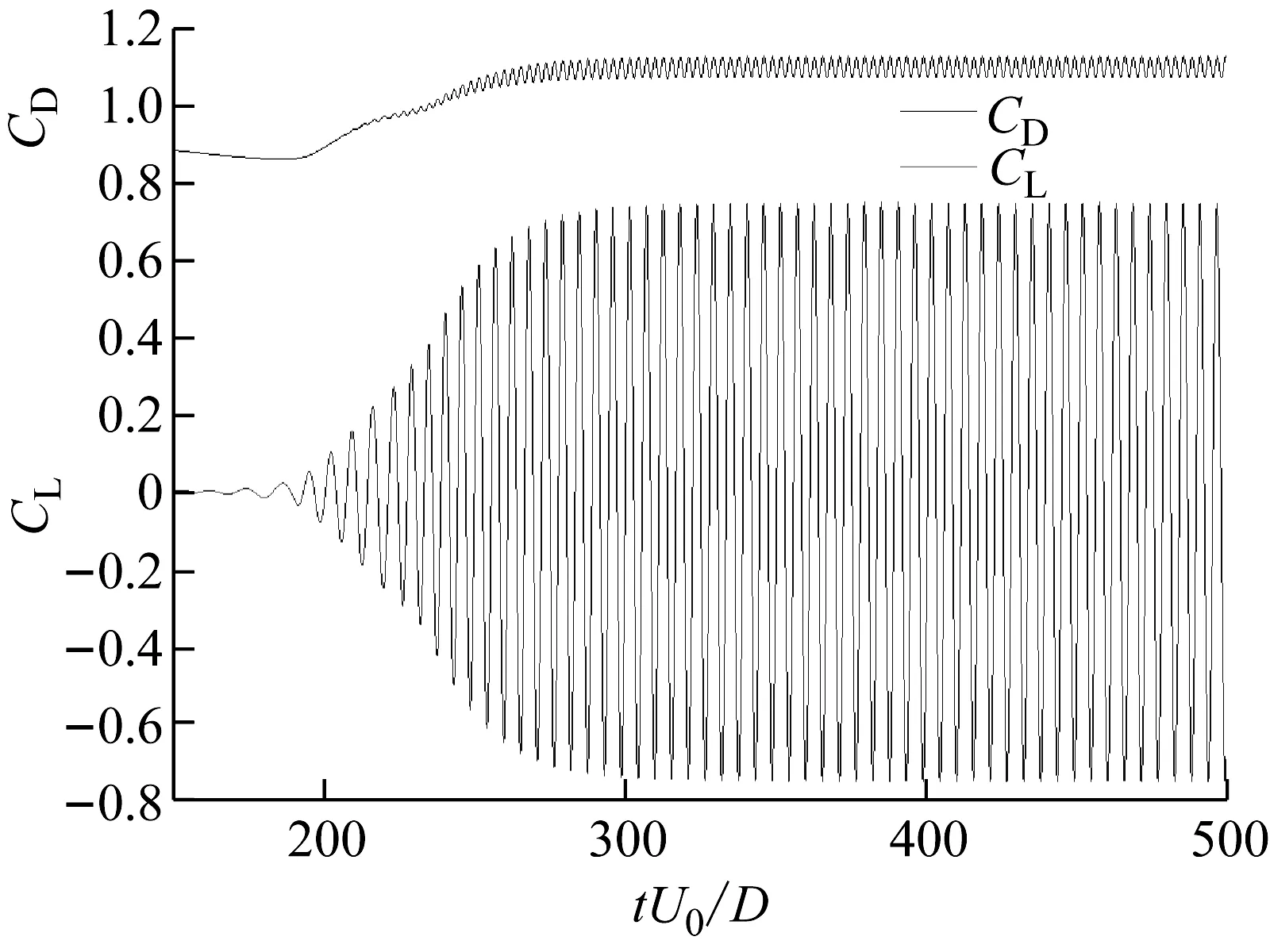
3 新月形覆冰导线气动力特性数值模拟
3.1 计算参数

3.2 气动力特性结果







4 结 论
