单自由度碰振模型擦边分岔分析
2020-05-18卢裕木吴文泽
卢裕木, 吴文泽
百色学院数学与统计学院,广西 百色 533000
机械振动产生一类特殊的动力学行为——擦边. 因为擦边,系统可以由周期运动进入混沌状态,产生各种各样的动力学现象. 许多学者也对系统擦边行为产生丰富的动力学行为的机理进行了深入研究. Nordmark[1]首次引入Poincaré-Nordmark局部映射对单自由度碰振系统的擦边运动进行了分析. 谢建华和罗冠炜[2~5]对一类碰撞振动系统的周期系统、环面分岔、余维二分岔等动力学行为做了详细分析以及混沌控制. Hu H Y[6]通过研究系统的擦边分岔,证实擦边分岔是系统由周期运动进入混沌状态的一种途径. 谭洁燕[7]通过Lyapunov指数谱分析了一类含对称刚性约束两自由度碰撞振动系统擦边轨道的稳定性. G W Luo[8,9]研究了一类含间隙受周期外力的两自由度碰振系统的参数多样性对周期运动的影响.李群宏和陈玉明在文献[10,11]中引入相对坐标讨论了对碰系统的Lyapunov指数谱稳定性判定问题. 本文针对一般的带刚性约束单自由度碰振系统,给出系统满足擦边余维二分岔的条件,数值模拟系统擦边余维二分岔点附近区域的开折图,用Lyapunov指数验证系统由于擦边分岔是系统进入混沌的一种方式.
1 力学模型
1.1 系统力学模型
单自由度碰振系统微分方程可表示为
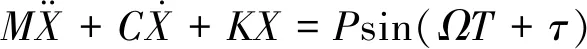
(1)
无量纲化后,方程为
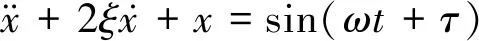
(2)
其中
振子M的冲击方程为
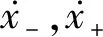
1.2 擦边分岔条件
根据文献[12]系统发生擦边余维二分岔的定义,我们可以归纳出下面的结论:
定理对于系统擦边点x*附近的碰撞点,如果满足条件
则系统发生擦边余维二分岔.
2 参数分岔分析
固定系统参数ω=3.99,同样地以变化b做扰动,当b=0.066 7时系统满足擦边条件,此时系统作混沌运动(图1(a)) ,时间历程图(图1(b))和Lyapunov指数图(图1(c)) 最大Lyapunov指数大于零.伴随着逐渐减小b的值,b=0.063时系统为一碰二周期运动(图2(a)),时间历程图(图2(b))和Lyapunov指数图(图2(c));b=0.05时系统为碰撞一周期运动(图3(a)),时间历程图(图3(b))和Lyapunov指数图(图3(c)).

图1(a)图1(b)

图1(c)图2(a)
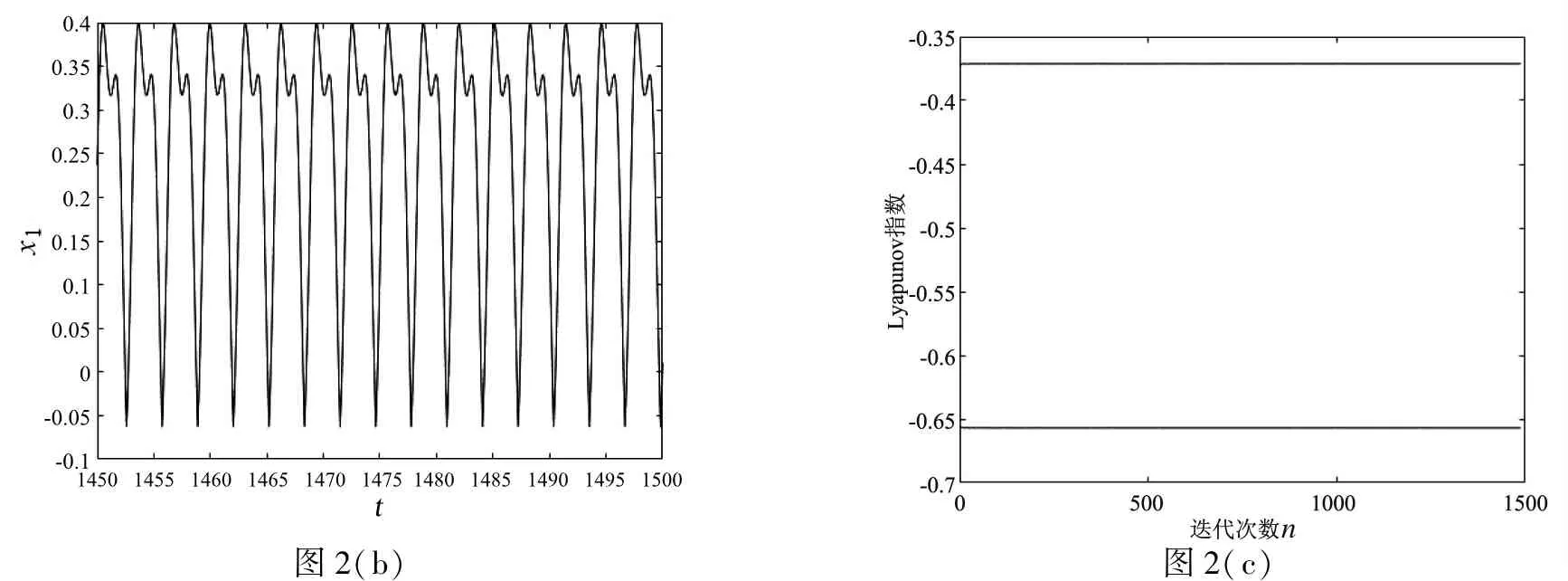
图2(b)图2(c)

图3(a)图3(b)
另一方面,观察b从b=0.066 7处逐渐增大,b=0.075时系统作混沌运动(图4(a)),时间历程图(图4(b))和Lyapunov指数图(图4(c)),最大Lyapunov指数为正数;b=0.08时系统作未碰一周期运动(图5(a)),时间历程图(图5(b))和Lyapunov指数图(图5(c)),最大Lyapunov指数为负数. 由以上的分析知,参数变化引起了的相图变化,擦边分岔同样是系统进入混沌的另一种方式.
通过上述数值模拟验证,最大Lyapunov指数大于零,系统做周期运动;最大Lyapunov指数小于零,系统出现混沌运动,表明了擦边分岔系统进入混沌的另一种途径.
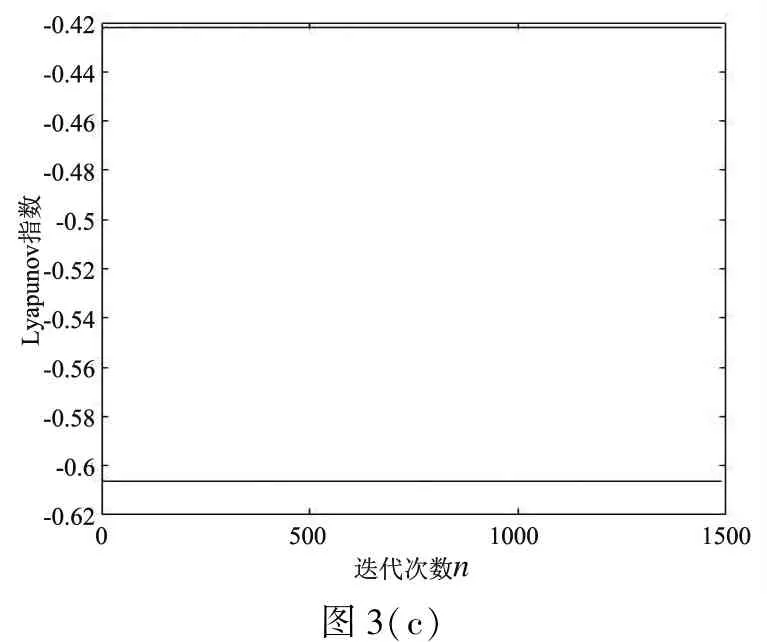
图3(c)

图4(a)图4(b)

图4(c)图5(a)

图5(b)图5(c)
3 结束语
碰撞振动系统由于擦边从周期运动进入混沌状态,产生丰富的非线性动力学现象.本文对一类单自由度含间隙刚性碰撞振动系统进行研究,首先给出满足系统发生擦边余维二分岔的条件. 然后画出系统满足余维二分岔点及其附近的运动相图,并且一一对系统运动相图的Lyapunov指数进行了验证,数值仿真表明Lyapunov指数验证系统周期运动和混沌运动的正确性,证实由参数引起相图结构的变化的分岔导致系统混沌发生.
