高拱坝浇筑条带协同的缆机群智能配置模型

赵春菊，闫楷文，刘 全，王 放，周华维

（1. 三峡大学水利与环境学院，湖北 宜昌 443002； 2. 三峡大学湖北省水电工程施工与管理重点实验室，湖北 宜昌 443002；3. 湖北工业大学土木建筑与环境学院，湖北 武汉 430072； 4. 武汉大学水利水电学院，湖北 武汉 430072）

0 引 言

混凝土拱坝超载能力强、安全性高，适于高山峡谷水资源开发［1-3］。缆索式起重机具有起重量大、覆盖范围广、机动性好等特点，可以横跨峡谷和河流等复杂地形，适用于高拱坝的混凝土浇筑［4，5］。为了高效施工，往往配置多台缆机组成缆机群浇筑大坝，小湾、溪洛渡、白鹤滩等拱坝的缆机台数均达到4 台以上［6-9］。

为了提高缆机群浇筑效率，通常利用多台缆机同时浇筑多个浇筑仓。此时，不同浇筑仓的混凝土运距不同，各台缆机的控制宽度不同，导致缆机之间吊运效率各异，进而造成浇筑循环时间和坯层覆盖时间差异，难以保证浇筑条带协同上升。加上缆机群共享轨道、塔架宽度和安全距离等因素的限制，缆机之间无法重叠和跨越，浇筑循环时间的差异可能会降低缆机的利用率，不利于缆机群发挥最大效能。因此，在多对多的缆机-浇筑仓优化配置问题中，期望各台缆机控制区域内的混凝土覆盖时间大致均衡，实现浇筑条带的协同上升和缆机群同步移位，对于提高施工效率意义重大。

近年来，已有众多国内外学者对拱坝浇筑中缆机配置优化的问题进行研究。王仁超等［10］构建了考虑空间冲突的缆机配置模型，为优化混凝土浇筑方案提供了依据。郭晓峰［11］从两仓联合浇筑的角度，根据优化目标，界定约束条件，提出缆机配置方案优选方法。王树强等［12］基于缆机群高低线协同控制系统，优化了缆机群调度配置。黄建文等［13］根据高拱坝施工数据分析结果及排队模型计算得到相关参数并建立目标模型，同时联合缆机群安全运行的边界方程取得最优的缆机配置。杨忠加等［14］基于高拱坝坝体生长特征与缆机配置之间的关系，优化了浇筑方案，提高了缆机的利用率。张志豪等［15］基于实时监控系统，通过定点下料的施工方法对缆机吊运混凝土的配置进行优化。在上述已有研究中对缆机优化配置在缆机之间作业干扰与联合、缆机施工数据分析结果、基于拱坝坝体生长特征以及仓面定点下料等方面取得成果，对于提高缆机群的安全高效运行具有重要意义。然而，在已有的研究中尚未考虑各台缆机的负载和浇筑循环时间差异对缆机群整体的施工效率的影响，因此有必要对缆机群的工作配置进行优化。

缆机群同时服务于多个浇筑仓时，单个浇筑仓又划分多个浇筑条带，按条带配置缆机和仓面的平仓机、振捣机进行下料、平仓及振捣配套作业。显然，缆机群与浇筑仓的匹配属于典型的多对多动态组合问题。针对组合优化问题通常可以运用传统算法进行求解，如0-x 算法［16］、线性规划［17］、非线性规划［18］、NSGA-II［19］、贪心算法［20］等算法。与普通的组合优化问题相比，缆机机动性强、服务组合方式灵活，仅从缆机和浇筑仓的层面进行浇筑组合遍历，组合规律难以提取，属于NP-Hard 在线装箱难题［21］，且其解空间容量十分巨大，直接求取必然面对“维数灾”，求解和优化非常困难。因此，复杂条件下考虑吊运负荷均衡的多缆机对多浇筑仓组合优化问题需要进一步研究。为此，本文提出一种“微匹配”的方法，将缆机覆盖范围与浇筑仓重叠的区域即浇筑条带进行微分化处理，在浇筑仓的微分条带内，缆机和条带之间可简化为一对一的关系，在此基础上建立求解模型。

综上所述，本文研究并提出了一种缆机群智能配置模型，以实现各缆机循环时间、负载比较均衡的优化目标。该模型首先对各缆机覆盖范围与浇筑仓重叠的区域进行浇筑条带划分，然后对浇筑条带进行微分化，通过微条带与微匹配建立缆机微条带一对一的匹配关系，并且根据浇筑匹配中的边界、约束条件和优化目标建立微匹配的积分表达实现缆机群与浇筑条带组合的优化。结合白鹤滩工程的缆机优化配置方案验证了本模型的可靠性和有效性

1 浇筑匹配模型

大坝浇筑过程可以看作是由缆机对浇筑仓服务逐步推动系统状态变迁的过程。当配置不同浇筑方案时，系统所占用的入仓资源（如缆机数量）不同，消耗的浇筑时间不同，服务的仓位不同，得到的坝体浇筑面貌也不同。因此，浇筑方案优化是大坝施工过程优化的核心。

实现浇筑方案优化需要先求解可选浇筑方案集，再根据优化目标从中选择执行方案。

设：可选浇筑方案PM即是入仓资源与浇筑仓之间的匹配关系，在本文中特指多台缆机与多浇筑仓的组合关系。可用缆机集{CC}和拟浇仓位集{Blk}的组合表示，如式（1）：

式中：CC参与浇筑的缆机；Blk为浇筑仓位。

某时刻四台缆机{CC1，CC2，CC3，CC4}浇筑两个仓位{Blk0，Blkk}以及所划分浇筑条带集合{Rng1，Rng2，Rng3，Rng4}的浇筑匹配如图1 所示。可见，浇筑匹配PM可用浇筑矩阵表示，矩阵中的匹配元记为pm，表示具体的缆机与浇筑仓的匹配，如图2所示。

图1 某CC和Blk的浇筑匹配示意图Fig.1 Match of pouring diagram of a CC and Blk

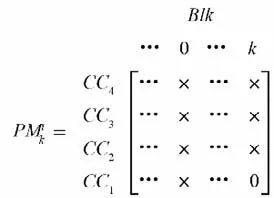
图2 某CC与Blk的匹配矩阵Fig.2 The matching matrix of some a CC and Blk

2 缆机智能配置模型

2.1 浇筑仓微条带

某一时刻存在浇筑匹配PM，PM.Blk为该匹配中的浇筑仓，根据平移式缆机覆盖的特点，将浇筑仓的缆机覆盖范围微分化为浇筑仓微条带PM.Str，如图3。

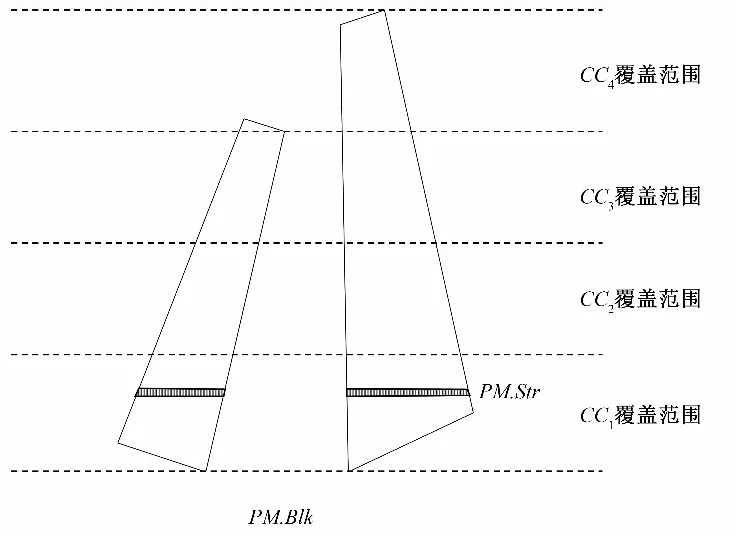
图3 浇筑仓位及微条带示意图Fig.3 Schematic diagram of pouring blocks and micro strip

2.2 基于微匹配的浇筑组合优化流程

在图3 中缆机覆盖的浇筑仓面划分的条带进行微分化，可建立浇筑组合优化的微匹配积分表达，对浇筑仓存在式（2）的积分：

式中：dl为垂直于平移式缆机方向的长度微元。

将缆机和条带多对多关系，通过微条带和微匹配转换为一对一关系，以便在微匹配层面处理浇筑组合优化问题，解法步骤见图4。

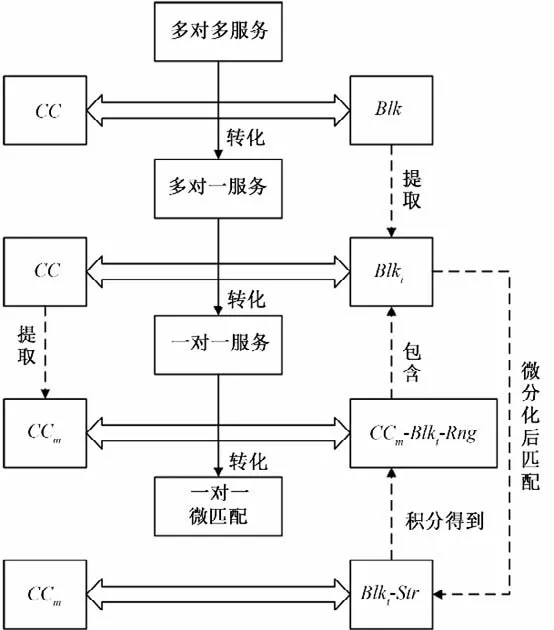
图4 微匹配的浇筑组合优化流程Fig.4 Micro match of pouring configuration optimization process

不失一般性，针对从浇仓位集Blk中提取仓位Blki，缆机集CC 中可选出某缆机CCm，根据其浇筑覆盖条带范围CCm.Rng可得到CCm针对Blki内的一个条带状浇筑控制区域CCm.Blki.Rng，该缆机与该条带即为一对一服务关系。但是，由于缆机的覆盖条带范围受到众多条件限制，难以统一。为便于处理均衡性等优化目标，将条带范围微分化，从微条带Blki.Str积分的角度反映缆机的覆盖关系。则浇筑微匹配组合可表达为式（3）：

2.3 浇筑匹配问题的基本施工约束

根据缆机浇筑作业规则，对于任一匹配组合存在施工边界约束：

（1）缆机下覆的浇筑仓坯层层间覆盖要求。根据各缆机覆盖范围内的面积、浇筑厚度和混凝土初凝时间，各缆机的浇筑强度需要满足层间覆盖需求。

（2）缆机群对浇筑区域的覆盖完备性。在各浇筑仓上的所有微条带必须保证在缆机群的覆盖范围内。

2.4 优化目标

缆机对浇筑仓的浇筑组合优化目标为：缆机群协同完成浇筑的时间短，各缆机间负载尽量均衡。

（1）缆机群浇筑的总浇筑强度最大。缆机对微条带的浇筑覆盖强度随距离增大而减小，即缆机的循环时间会增长。为了尽快完成浇筑任务，总体上希望缆机群浇筑的总强度最大，循环时间优化目标的表达见式（4）。

式中：pmmCC为缆机m的匹配组合，pmmCC.Pwr为缆机m匹配组合中的总浇筑强度。

（2）缆机间的负载均衡。对各缆机而言，希望缆机间负载均衡，方便缆机间协调。负载均衡的优化目标表达见式（5）。

式中：var{pmmCC.Pwr}为缆机m匹配组合总浇筑强度的负载方差。

2.5 智能配置

在常态混凝土拱坝浇筑过程中，受河谷形状、相邻高差、坝身结构、浇筑资源等多因素影响，各坝段交错上升，浇筑仓的约束状态随之动态变化。当某一仓的浇筑作业开始或结束时，缆机资源的闲/忙状态也随之转变。因此，在进行缆机浇筑作业匹配规划时，可利用的缆机工作台数与可浇筑仓的数量和空间分布关系随时间动态变化。本模型在空间中对缆机群下覆面积进行空间微分/积分，动态匹配缆机与浇筑仓，在微观上优化缆机与微条带之间的组合关系；在宏观上，实现缆机负载的均衡和缆机群高强度浇筑，充分利用缆机群的运输能力来完成浇筑任务。通过建立的微匹配模型，拱坝仿真系统通过遍历调整微匹配与缆机之间的组合关系来自适应动态变化的条件，利用迭代优化均衡缆机—微匹配—浇筑仓组合关系，均衡缆机之间负载，优化缆机群浇筑的总强度，实现缆机群智能配置。

3 案例研究

白鹤滩工程采用双层布置的7 台（4+3）平移式缆机浇筑。某时刻拟同时浇筑7、13、15 号坝段仓位如图5。仓位基本信息如表1。针对7 台缆机对3 个浇筑仓的组合优化问题。利用本文提出的缆机智能配置模型，可解算得到7、13、15 号坝段仓位及浇筑缆机群间的组合匹配关系，如图5所示。

表1 案例坝段仓位基本信息Tab.1 bBsic specifications of dam blocks

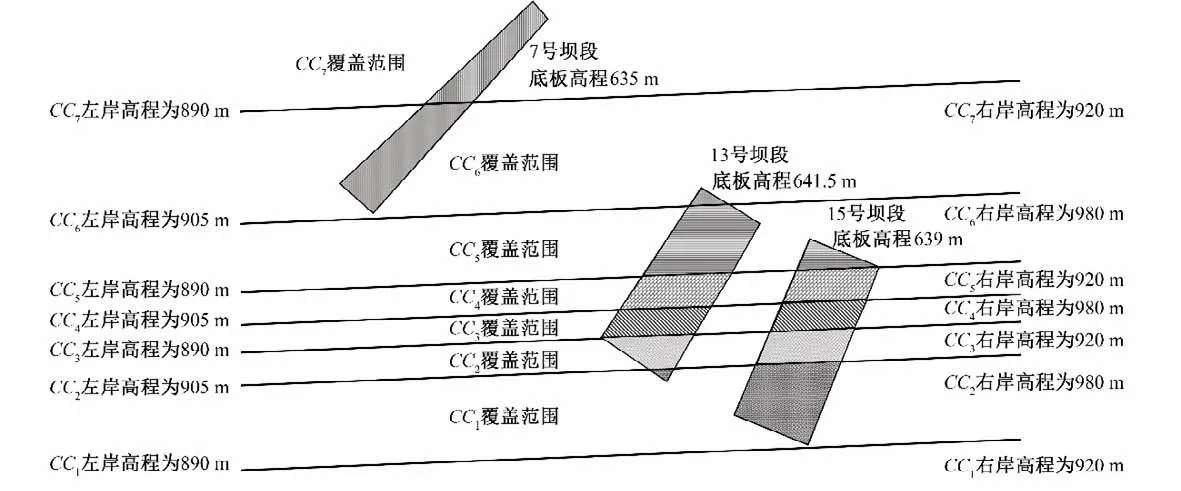
图5 坝段仓位空间位置及缆机集基本信息Fig.5 Spatial position of dam blocks and basic information of cable cranes

案例的覆盖浇筑组合矩阵见图6，基于缆机群智能调配模型解算得到各缆机覆盖浇筑条带的浇筑强度如图7，各缆机覆盖的浇筑仓面积如图8。

图6 案例的覆盖浇筑组合矩阵Fig.6 The coverage pouring configuration matrix of the case

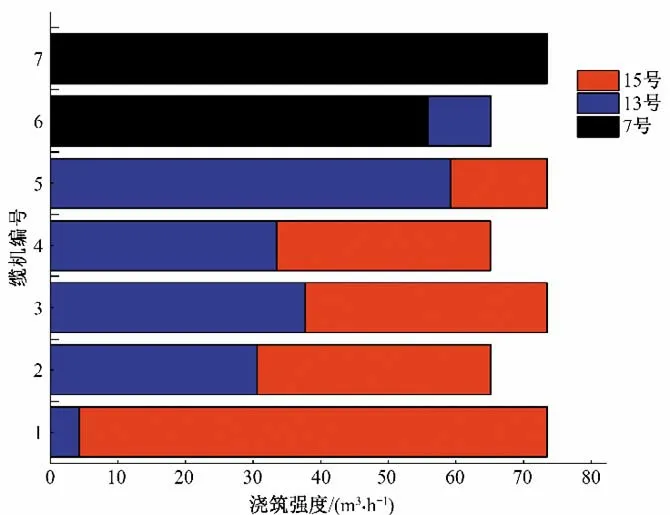
图7 缆机坝段仓位对应浇筑强度Fig.7 The position of the cable dam blocks corresponds to the pouring strength

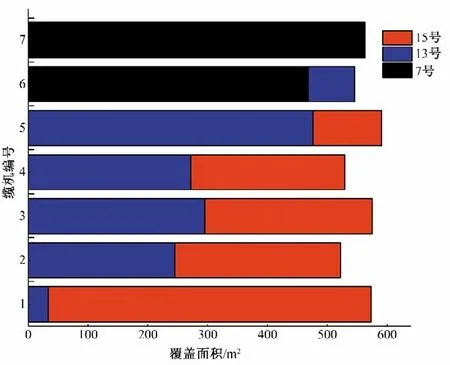
图8 缆机坝段仓位对应覆盖面积Fig.8 Corresponding coverage area of cable crane dam section

由图7、图8 可知，根据浇筑强度与覆盖面积可以得到缆机的作业时间。缆机1～7 号对其覆盖的面积下浇筑强度基本接近，经过计算1～7 号缆机的平均浇筑强度为69.9 m3/h。进而可以计算得到1-7号缆机基于平均浇筑强度偏差，如表2所示。

表2 各缆机的作业时间和强度偏差Tab.2 Cycle time and strength deviation of each cable crane

由表2可知，各缆机的作业时间基本均衡，说明各缆机覆盖的面积与其所覆盖的浇筑条带范围内的浇筑强度基本保持均衡，即保证了浇筑条带的协同上升。1、3、5、7 号缆机同为下层缆机且浇筑强度偏差均为5.1%，2，4，6 号缆机同为上层缆机且浇筑强度偏差均为-6.8%，1、3、5、7 号缆机与2，4，6 号缆机分属不同的平台，且分配的条带尺寸也稍有差异，故浇筑强度偏差不同，但是同平台的缆机负载均衡，且上下平台的偏差量基本接近，可以实现缆机群的同步移位，提高浇筑效率和保证施工安全。

综上所述，本模型对缆机群的调配实现了循环时间和负载的优化目标。在仓面条带范围内，各缆机可以实现协同上升、同步移位。实例证明本文模型具有良好的稳定性和实用性，对缆机群和浇筑仓进行了较好的配置。

4 结 论

考虑浇筑条带间缆机协同浇筑和上升，建立缆机群浇筑的智能调配模型，并运用在白鹤滩拱坝浇筑仿真中，得到以下结论。

（1）提出基于微匹配的浇筑组合优化模型。通过引入微匹配将缆机和浇筑仓条带之间多对多关系转换为缆机和微条带之间的一对一关系；进而建立基于微匹配的浇筑组合的积分式，表达缆机群总强度和负载均衡的优化目标，构建了缆机群浇筑的智能配置模型，利用迭代优化求解。

（2）本文建立的缆机群和仓位浇筑组合优化模型，在白鹤滩等工程的浇筑施工仿真中运用取得了良好的优化效果。对可变数量的缆机同时浇筑多个浇筑仓的复杂情况，具有较好的求解适应性和稳定性。在拱坝施工数字孪生系统中，可预测拱坝浇筑历时，并可作为缆机群浇筑活动的数值分析核心。