载人月球车稳定操控策略设计与优化

曹剑飞，梁常春，王 瑞，王耀兵，王志福，王 军

(1. 北京空间飞行器总体设计部空间智能机器人系统技术与应用北京市重点实验室，北京 100094；2. 北京理工大学机械与车辆学院，北京 100081)

0 引 言

以星球车为主的星表活动技术是满足人类大范围探测地外行星及建立长期基地的关键技术[1]。由于星球表面的特征及未探测区域存在较大不确定性,为了能够实现短期、长期乃至于永久性驻留,就必须通过具备高速移动能力的星球车来实现大范围月面环境探索[2]。

与现有在轨应用的无人月球车相比,载人月球车能够通过航天员驾驶实现更大范围、更高效的月面移动行驶,针对其移动操控策略的方案设计及功能开发对于完成地外星球科研探索任务意义重大[3-4]。

与地面车辆相比,载人月球车首先要克服的困难就是月面低重力环境造成的各项不利影响[5-6]。这些影响包括:低重力导致的低附着特性会造成车辆驱动能力受限,给车辆高速平稳移动控制带来不小的挑战;非结构化地形条件极易导致车辆四轮受力不均匀,高速行驶的振动特性在低重力条件下更容易造成车轮腾空,对安全平稳驾驶造成不利影响;此外,受限于宇航产品固有的体积质量严苛约束,载人月球车本身不具备机械转向拉杆及分动装置,各车轮的驱动转向均为独立控制。在提升操控自由度的同时,也对多动力执行机构的协同控制提出了新的要求。

因此,本文针对特殊地形星表载人巡视探测需求,设计了一种基于分层架构的载人月球车移动操控策略,并针对稳定转向及安全报警需求分别设计了差动制动控制策略与车轮腾空监测策略。基于仿真环境完成了系统建模及控制策略性能仿真分析,在原理样机研制基础上,对其功能、性能等进行了试验验证。

1 系统概述与技术方案分析

1.1 载人月球车基本结构

载人月球车基本结构见图1。该车属于典型的分布式驱动轮式底盘,每个车轮可通过轮毂电机实现独立驱动,同时每个驱动车轮均可通过独立的转向机构实现转向角度调整。

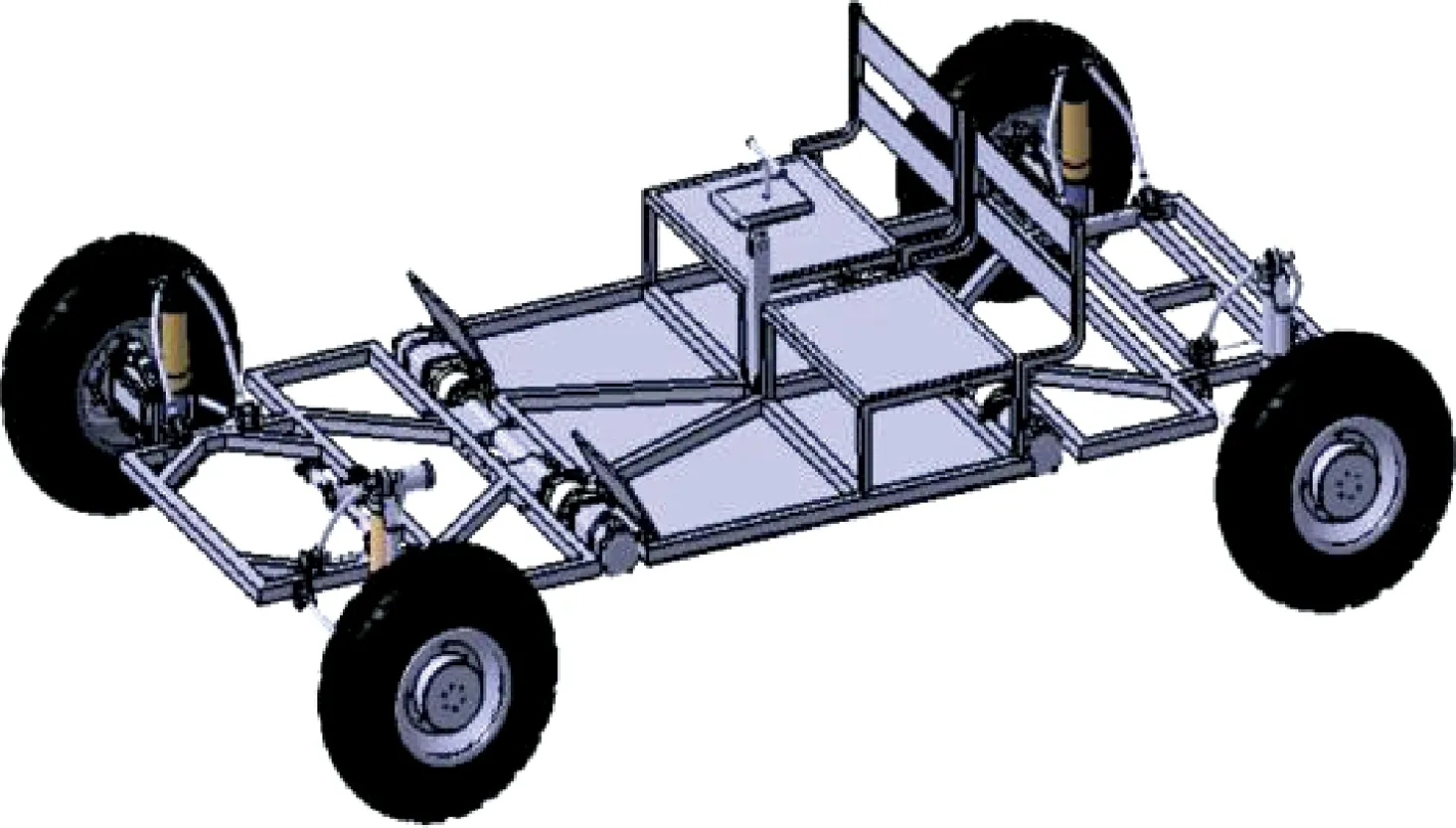
图1 载人月球车数字模型Fig.1 Digital model of the manned lunar rover

载人月球车的控制硬件系统(图2)包括了整车控制器、各类必要环境感知传感器及惯性测量单元(IMU)等。通过这些传感器,整车控制器可以实时获取各车轮的转速、转角信息,以及车辆质心处的三轴加速度与角速度信息,通过合理设计控制策略,将车轮转向指令和驱动力矩指令下发给电机控制器,实现整车移动控制。

图2 载人月球车控制系统结构Fig.2 Control system configuration of the manned lunar rover

1.2 技术方案工程适应性分析

为确保载人月球车能够有效克服各项不利因素,实现既定工程目标,移动操控算法的设计应充分借鉴来自地面车辆的各项先进经验[9-14],并根据宇航产品特性进行工程适应性分析,以确保功能有效实现。

作为一个冗余驱动系统,月球车执行器数量(驱动转向电机单元)远大于控制指令数量(来自航天员的驱动转向信号),因此选择了分层结构来设计总体控制方案,以充分发挥分布式动力总成结构优势,实现车辆运动学目标与执行器动力学控制量的分离,提升驾驶意图跟踪精度。

考虑到车辆系统固有的非线性误差及不可测干扰,驾驶意图跟踪控制器必须要具备一定的抗干扰能力,即在环境条件与系统模型失配的情况下仍能保持良好控制效果。因此,滑模控制被用于上层运动控制器的设计。该方法对系统参数变化及外界扰动不敏感,鲁棒性强,同时其数学描述简单,运算速度快,从环境适应性及计算效率上考虑均适用于载人月球车的控制系统。

在主动安全功能设计上,地面车辆的成熟技术大都采用了多目标集中控制方法。改方法尽管功能全面,但耦合性强,计算成本高,对于资源有限的深空探测任务来说并非最优方式。考虑到工程任务特点,本方案应根据具体风险场景进行针对性设计。

因月壤松软,航天员在起步加速及高强度制动过程中极易出现车轮打滑现象,不仅影响驱动性能,还会过度磨损车轮,因此,应通过设计滑移率控制功能实现驱动防滑。此外,因月面光照条件复杂,行车视线差,航天员很难避免高速行车过程中进行大角度转向操作,如不加以控制,因侧向力不足及轴荷转移引起的侧倾运动极易发展为侧滑侧翻等危险状况。故响应的预防功能也应当包含在控制策略设计中。

此外,高速行驶的月球车还很容易在非结构化月面(平整度差)上出现间歇性车轮腾空。此时部分车轮驱动力缺失,容易出现横摆不稳定现象,尽管分层控制架构下能够通过全轮矢量控制弥补这一缺陷,但仍需要通过一定技术手段对该现象进行监测报警,以提醒航天员采取主动措施来避免风险。

1.3 整车期望性能指标设计

为满足功能测试验证需求,本文设定了如下几项期望性能验证指标。其中,滑移率控制(驱动防滑基础)和车轮离地检测均采用直接验证方式;而分层控制系统的稳定性和防侧滑侧翻功能验证则是通过特定工况行驶时的关键状态参数范围予以识别。这里特别要说明的是,尽管地球环境无法模拟出低重力条件下的侧滑侧翻情况,但通过关键状态参数的核算,能够推算出月面条件下的车辆实际情况。因此,只要关键参数符合设计指标,即可说明功能目标达成。

1)驱动防滑指标:在典型对开路面,速度从0到最大行驶速度、加速时间≤10 s情况下,车辆摆动角不大于2°;

2)差动转向指标:以最大行驶速度转向时,车辆外侧滑移率不超过20%,内侧滑移率不超过20%;原地转向时间不大于30 s(滑移率为统一概念,具体到驱动和制动工况,也可分别称作“滑转”和“滑移”);

3)车身自主稳定指标:能够以最大行驶速度通过J路测试;

4)轮离地检测指标:车轮离地时间超过0.2 s即触发离地检测预警。

2 移动操控策略设计

2.1 分层控制策略架构

从系统输入上看,载人月球车仅能通过航天员接收到2组控制指令:驱动信号与转向信号。操控设备无论是采用“方向盘+油门”配置或是采用类似于阿波罗月球车的操纵摇杆配置,这一点都不会发生变化[7-8]。而作为执行机构的车辆底盘却有8组执行机构来响应控制输入(4组驱动电机+4组转向电机)。因此,这是一类典型的过约束系统,为了合理实现驾驶员意图识别并将其分配给各执行机构,本文采用了分层架构来实现整车移动操控需求,如图3所示。

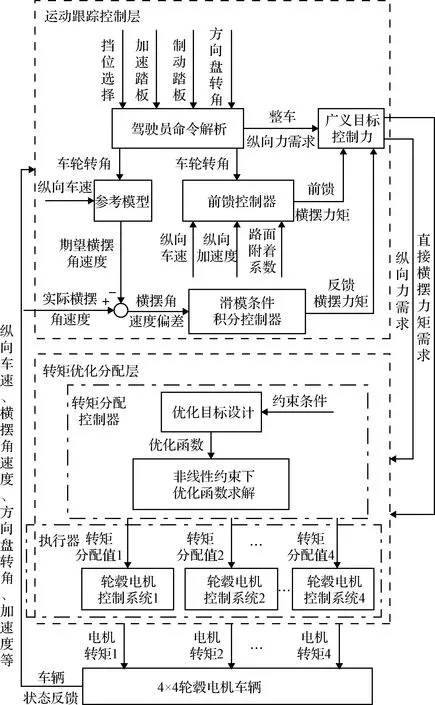
图3 基于分层结构的操纵稳定性控制策略Fig.3 Stability control strategy with hierarchical structure

所述的分层架构整体上分为2个层级,包含上层车辆运动控制器和下层车轮力矩分配控制器。而下层的车轮力矩控制器又进一步包含了车轮转矩优化分配控制与期望车轮力矩跟踪控制2个部分。其中上层控制器采用滑模控制算法重点解决车辆整体运动状态控制[9-10];下层控制器采用最优控制分配方法重点解决约束条件下的车轮力分配控制[11-12],并提出了误差跟踪和性能优化双重目标函数,约束条件下的车轮力分配采用积极集方法进行求解;期望车轮力跟踪控制器采用滑模控制算法实现对由逆轮胎模型计算得到的期望滑移率和侧偏角的跟踪,并最终计算得到各执行器的具体输出以达到指标要求,其计算流程如图4所示。

图4 移动控制流程图Fig.4 Workflow of mobiling control strategy

2.2 月球车参考状态生成

无主动悬架情况下,车辆的操纵稳定性主要受横摆角速度和质心侧偏角影响(质心侧偏角定义为车辆质心速度矢量与车辆几何前方的夹角)。兼顾考虑纵向车速要满足航天员驾驶需求,故选择期望纵向车速、期望横摆角速度和期望质心侧偏角作为车辆的参考状态[13-14]。

1)期望纵向车速计算

期望纵向车速按照如下公式计算

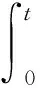
(1)

式中:vxd为车辆初始速度;axd为期望纵向加速度,由踏板给出指令。

2)期望横摆角速度和期望质心侧偏角计算

采用经典的二自由度动力学模型[15]完成期望横摆角速度和期望质心侧偏角计算。其中,二自由度动力学模型公式如下:

(2)

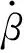
据此,当车辆在稳定状态时,可以求解得到期望横摆角速度如下:

(3)

其中,中间变量A和B的含义如下:

(4)

较大的质心侧偏角对于车辆稳定行驶是不利的,因此期望质心侧偏角可以取βd=0。

2.3 上层车辆运动控制器设计

仅考虑整车在平面上的纵向、横向和横摆运动,3个自由度对应的运动微分方程如下:

(5)

(6)

(7)

式中:Fxc,Fyc为x,y方向驱动力;Mzc为绕z轴的横摆力矩;FR为运动方向阻力;ξ为扰动。

由此可知,车辆的纵向车速、质心侧偏角和横摆角速度可分别通过纵向合力、横向合力与横摆力矩来进行跟踪控制。为避免不确定误差干扰造成的控制失配,本文采用了滑模控制方法实现3项指标的跟踪控制。

滑模面选择均为实际状态与期望状态的差值,即:

sv,x=vx-vxd

(8)

sω,z=ωz-ωzd

(9)

sβ=β-βd

(10)

(11)

据此,为实现纵向车速跟踪所需的期望纵向合力为

(12)

与之对应,侧向合力与横摆力矩的控制也具有相似关系

(13)

(14)

2.4 上层车辆运动控制器稳定性分析

为了分析采用滑模控制方法的稳定性,需构造如下的李雅普诺夫函数[16-17]:

(15)

对于本文所述的滑模面定义方法,当系统进入滑模运动时,李雅普诺夫函数的一阶导数满足

(16)

因此,系统的滑模运动稳定于滑模面s=0。

2.5 下层驱动转矩分配控制器设计

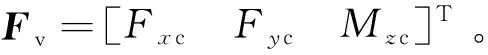
根据车辆动力学关系,目标控制力(力矩)与轮胎纵向力之间存在如下对应关系:

v=B·u

(17)

式中:v为目标控制力(矩)Fv,即

(18)

u为轮胎纵向力和侧向力:

(19)

B为系数矩阵,B∈R3×8:

(20)

其中:

B1=[cosδ11,cosδ12,cosδ21,cosδ22,-sinδ11,-sinδ12,-sinδ21,-sinδ22];

B2=[sinδ11,sinδ12,-sinδ21,-sinδ22,cosδ11,cosδ12,-cosδ21,-cosδ22];

式中:B表示轮距,L1和L2表示轴距。

理想情况下应实现v=B·u,但是对于冗余执行系统来说,该方程可能是无解、有唯一解和无穷多解等情况。因此,采用解析方式求解约束方程可能是无效的。据此,通过定义2组目标函数来完成对上述公式的求解。

1)误差逼近目标函数

定义基于l2范数的误差逼近目标函数J1:

J1=(||Wv(Bu-v)||2)2

(21)

式中:Wv为对角的加权矩阵,代表所对应的期望合力/力矩在误差逼近目标函数中的重要程度,即

Wv=diag(WFxc,WFyc,WMzc)

(22)

式中:WFxc,WFyc,WMzc分别为Fxc,Fyc,Mzc对应的权重。Wv可以对目标控制力(矩)v中元素的权重进行调整。

2)性能目标函数

性能目标函数的选取主要着眼于驱动系统效率和车辆稳定性优化。在车辆运动过程中,受轴向载荷转移等因素的影响,可能会出现某一车轮已经达到附着极限而另一车轮仍有较大的轮胎力储备的情况,不利于整车操纵稳定性控制。为此可基于轮胎负荷率的概念定义性能目标函数,使得所有轮胎的负荷率之和最小,保证各轮受力均匀、附着性能良好。

首先定义轮胎负荷率ρij:

(23)

式中:μ·Fzij代表轮胎的最大附着力。定义性能目标函数J2:

J2=(||Wuu||2)2

(24)

式中:Wu为对角加权矩阵,即

(25)

其中,λij为加权因子,代表对应车轮负荷率的权重值。

由加权最小二乘方法,可以得到综合目标函数J及下层控制器实际控制输出u:

J=J1+J2=η(||Wv(Bu-v)||2)2+(||Wuu||2)2=

(26)

式中:η为协调因子,一般取较小值,从而在求解最优解的过程中优先保证误差逼近目标函数值较小,更好地达到驾驶员驾驶意图。上式可通过“有效集法”进行求解,最终计算得到各轮期望纵向/侧向力[18-20]。

此后,进一步通过轮胎滑移率及侧偏角控制,实现期望纵向/侧向力的跟踪,确保车辆能够在避免过度滑移的情况下实现稳定的动力输出。

3 主被动安全策略设计

3.1 驱动防滑控制

在车轮坐标系xwowyw上,轮心沿纵轴方向的速度为

vwxi(l,r)=vxi(l,r)cosδi(l,r)+vyi(l,r)sinδi(l,r)

(27)

得到车轮的滑移率为

(28)

式中:ωwi(l,r)为各轮的旋转角速度;R为车轮滚动半径。显然-1≤λi(l,r)≤1,当λi(l,r)≥0时,表示车轮滑转;当λi(l,r)<0时,表示车轮滑移。

对于所述载人月球车原理样机来说,滑移率的控制可以通过轮毂电机和制动器的输出力矩来实现(实际上是通过逆轮胎模型计算出期望力矩对应的期望滑移率)。由于被控系统复杂程度高、不确定性强,结合驱动防滑任务特点,选择了基于滑模变结构方法来实现驱动防滑控制,能够有效提升控制效果的鲁棒性[21]。其原理如图5所示。

图5 驱动防滑策略流程图Fig.5 Workflow of anti-slip control strategy

与上层控制器跟踪方式相似,首先设计滑移率控制的滑模面如下:

sκ=κ-κd

(29)

对式(29)进行求导,得到:

(30)

由于车轮滑移率在驱动/制动工况下的定义不同,所以需对其进行单独讨论。

1) 驱动工况滑移率跟踪控制

驱动工况下的滑移率表达式为

(31)

代入车轮旋转运动微分方程式有:

(32)

同样选择带饱和函数的等速趋近律对抖振问题加以抑制,最终得到所需轮胎牵引力矩为

(33)

2) 制动工况滑移率跟踪控制

制动工况下的滑移率表达式为

(34)

因此,该状态下最终计算得到的轮胎牵引力矩为

(35)

通过滑移率控制,可以确保车轮能够尽量保持在线性工作区间,避免过度滑移/滑转造成整车失控。

3.2 防侧翻控制

从车辆运动来说,侧翻可以看作车辆侧倾运动的一种危险情况。车辆在曲线运动中会产生一定的载荷转移,当车辆的侧向加速度或横摆角速度超过一定值后,内侧车轮的垂向载荷会减小为0,从而引起一侧车轮离地。

本文采用车辆横向载荷转移率(LTR)来识别侧翻运动风险[22]。其定义如下:

(36)

当侧翻检测系统检测到的车辆橫向轴荷转移率大于所设定的安全阈值,就会触发防侧翻控制系统。本文采用差动制动方式来实现防侧翻控制。该功能处罚的数学表达式如下:

(37)

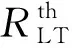
由于所研究的载荷情况不定,且工况均为侧翻危险工况,故将阈值设定为0.7,当大于或等于0.7时,即进行差动制动防侧翻控制,对前轴外轮及中后轴外轮进行单独制动,此后不再进行侧翻检测;触发控制后,控制车辆的侧向加速度,如果加速度降低到设定阈值以下,则停止差动制动;否则将持续进行加速度控制。差动制动流程见图6。

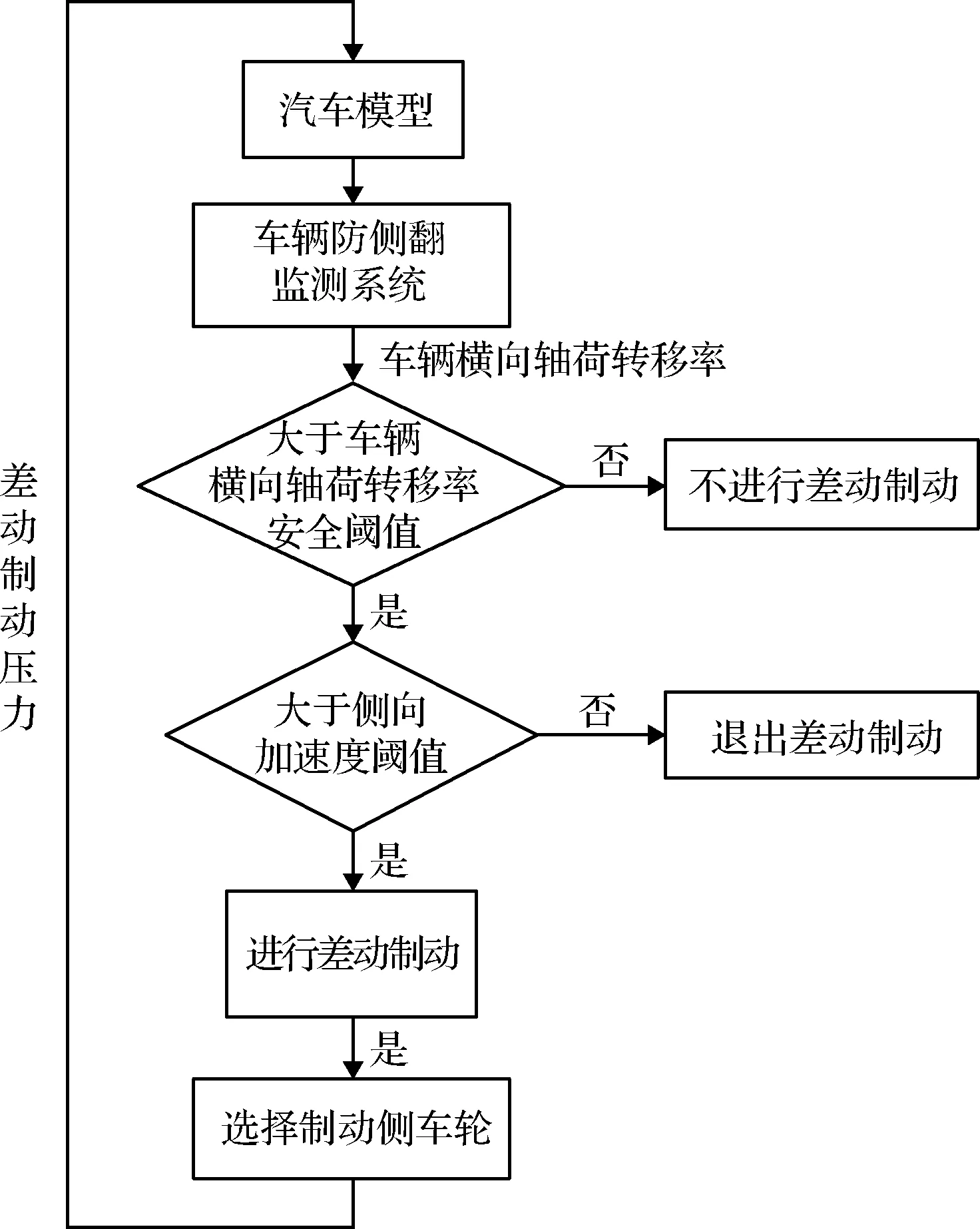
图6 差动制动控制流程Fig.6 Workflow of differential braking control strategy

3.3 离地检测

载人月球车在在崎岖月面行驶时,部分车轮容易出现离地现象。此时,通过对离地的车轮发出预警,可以有效提醒航天员去注意整车姿态的危险变化,属于一类非常实用的被动安全功能。

当载人月球车在正常行驶时,车辆加速度满足如下关系:

(38)

式中:Ft为驱动力;Ff为滚动阻力;Fs为坡道阻力;Fw为空气阻力;mδ表示考虑旋转质量换算后的整车质量;dvx/dt表示纵向车速对时间的导数,即加速度。

由上述公式可知,驱动力、滚动阻力、坡道阻力都是车辆在地面行驶时才会出现,当车辆腾空时,驱动力、滚动阻力、坡道阻力都为0。星球环境无空气或较稀薄,空气阻力假设为0。所以当车辆腾空时整车的加速度为0,水平方向的加速度也为0。

车辆在行驶的过程中腾空,航天员对车的驱动力保持腾空之前的状态,假定整个腾空过程驱动力不变,腾空时无阻力的4个轮子必定会产生过度滑转,会触发驱动防滑的功能,车轮的驱动力会下降,电机转矩便会下降,当前时刻的电机转矩会小于上一时刻的电机转矩。当车辆处于腾空状态时,在驱动防滑策略的作用下,驱动力会继续下降,驱动力矩下降的阶跃信号会一直存在,据此可实现车轮离地识别。

该过程执行流程如图7所示,当车辆启动时和正常行驶,单一的整车水平加速度和电机转矩阶跃信号出现时,并不会使能离地检测系统。只有整车水平加速度和电机转矩阶跃信号两种信号同时出现,才会使能离地检测系统。离地检测系统使能便会开始计时,当离地时间达到一定时间时(如0.2 s)便会向航天员发出预警信号。

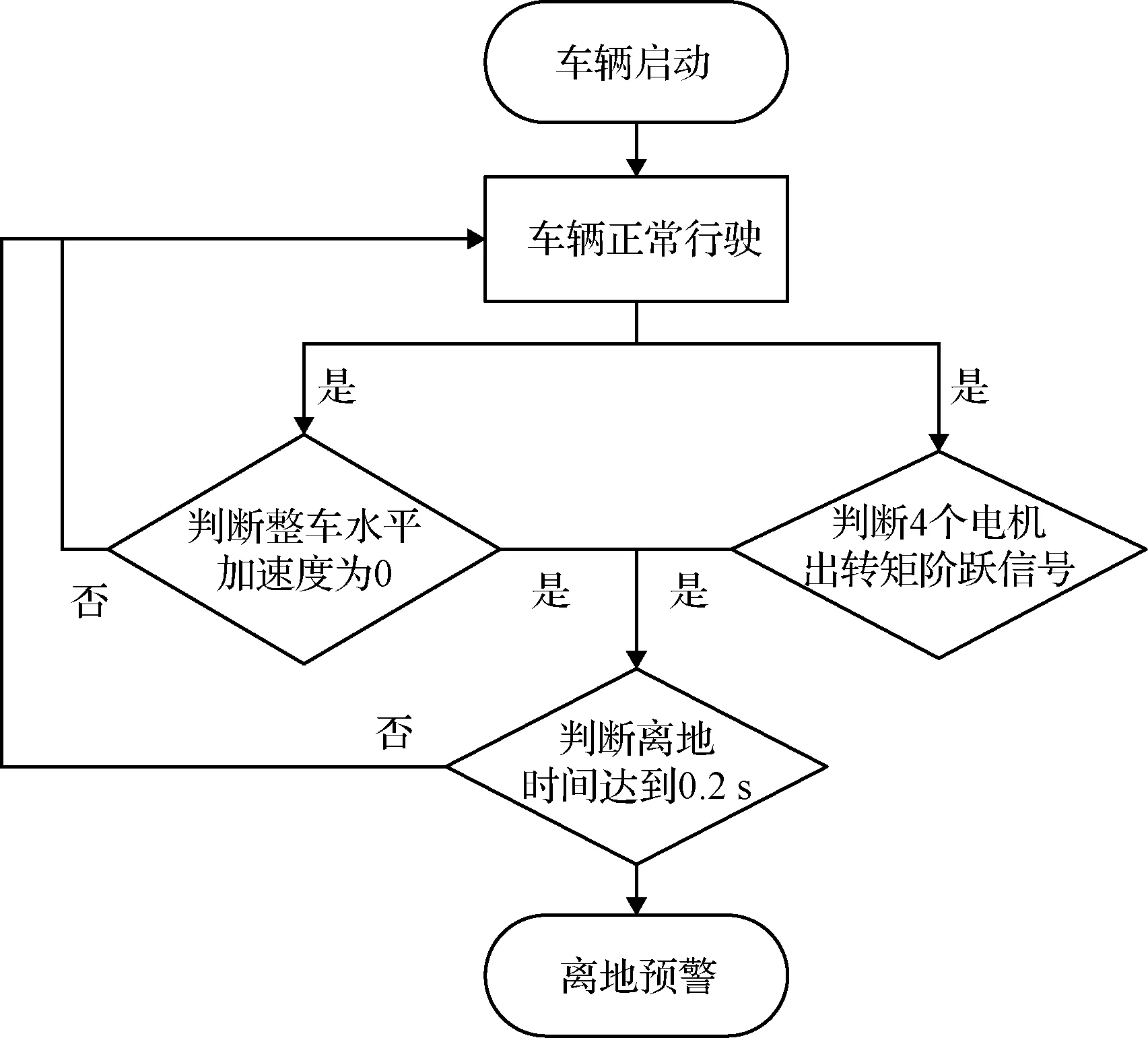
图7 离地检测流程图Fig.7 Workflow of ground-off detection

4 移动操控策略仿真分析

4.1 被控车辆建模

为了充分验证所设计的移动操控策略性能,本文建立了14自由度车辆动力学模型[23],用以分析和改进策略控制效果。模型的14个自由度包括:车身纵向、侧向、垂向以及横摆、侧倾、俯仰6自由度、4个车轮的滚动旋转自由度和考虑悬架垂向振动的4个自由度。车轮在水平面的转角运动仅通过运动学关系来描述,无动力学微分方程,故不计入自由度。

作为被控对象的车辆模型通过MATLAB/Simulink环境搭建,由于建模本身不是本文研究重点,故其细节此处不再赘述。

4.2 仿真分析

1)对开路面仿真

当路面条件为左侧附着系数0.4、右侧附着系数0.8时,驱动车辆进行匀加速直线行驶;初速度为1 km/h,加速度为0.5 m/s2,仿真时间10 s。仿真结果如图8所示。

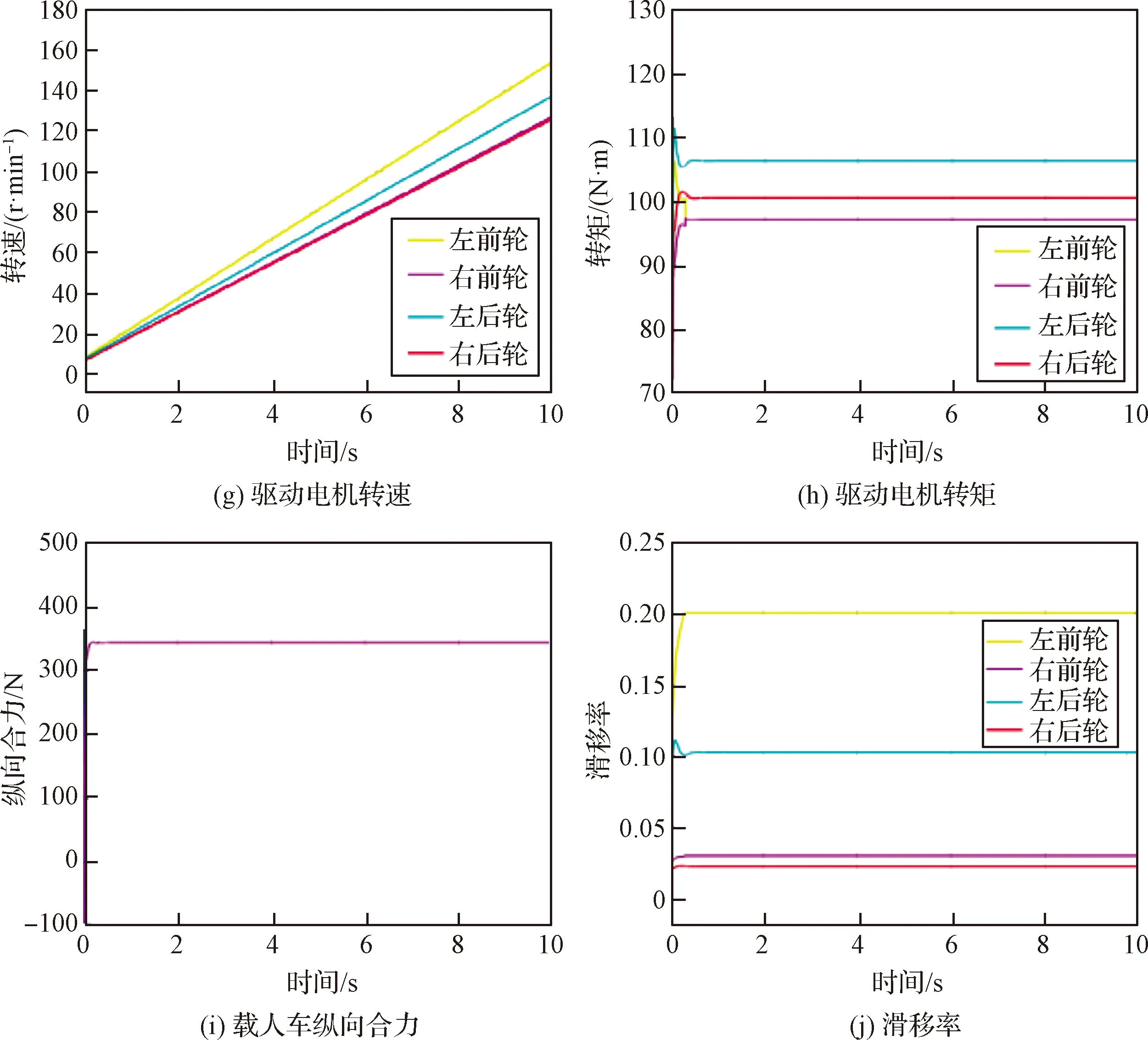
图8 对开路面仿真结果Fig.8 Simulation results of split pavement

从仿真结果可以看出,由于左侧路面附着系数较小,因此左侧车轮滑移率会比右侧车轮大,当超过期望最大滑移率0.2时,防滑模块会限制左侧车轮转矩,同时也会降低右侧车轮转矩。由于两侧附着系数不同,车辆会产生较小的侧向速度和横摆角速度,因此下层分配的左右侧车轮力也有所不同。

2)135°方向角阶跃响应

设定仿真条件为:轮地附着系数为μ=0.8,初始车速vx=10 km/h,2 s时方向盘转角由0增加到135°,之后维持135°到10 s仿真结束。车辆运动情况如图9所示。

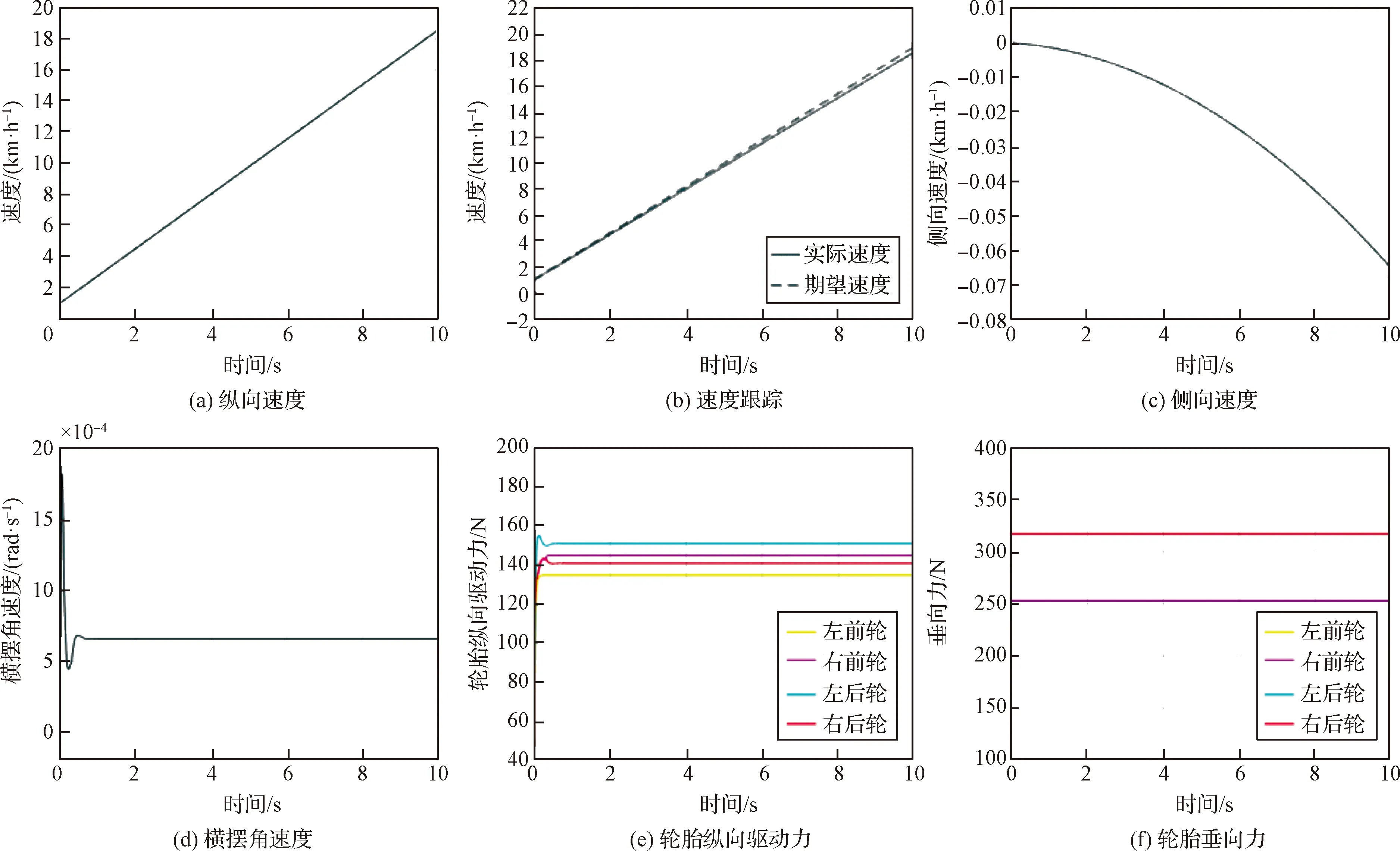
图9 135°转向性能仿真Fig.9 Simulation results of 135° steering control

由车辆运动特性图可以看出,载人车在转弯行驶时,车辆纵向速度跟踪期望车速10 km/h误差较小,横摆角速度控制效果良好,最终稳定在0.22 rad/s,侧向稳定性良好,各车轮滑移率很小,车辆行驶轨迹满足预期。

3)车轮离地功能监测

离地检测通过观测车辆加速度和车轮转矩变化从而判断车辆是否离地,由于该功能在地面重力条件下验证困难,故只进行仿真验证。

设置车辆在0～2 s以0.5 m/s2加速度行驶,此时4个电机转矩均为94 N·m,在2 s时,车辆离地,加速度变为0,4个电机转矩在驱动防滑模块作用下均降至58 N·m,观察2.2 s后报警模块是否使能。

从图10结果可以看出,当车辆加速度在2 s变为0,电机转矩在2 s均下降时,持续0.2 s后,离地检测模块使能,报警信号从低电平变为高电平,证明离地检测算法的可行性。

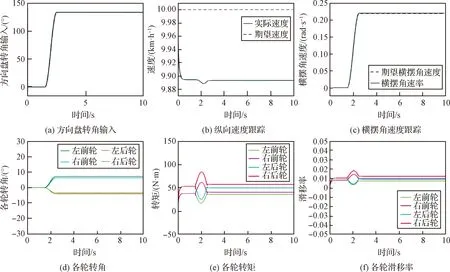
图10 离地监测能力验证Fig.10 Simulation results of off-ground detection

5 试验研究

5.1 试验条件

在完成载人月球车原理样机搭建完成后,基于快速原型开发控制完成整车移动操控策略的工程化开发,对控制系统及各功能模块进行验证。原理样机见图11,整车轴距2.23 m,轮距1.15 m,可通过遥控器远程操作实现给定移动指令执行。

图11 载人月球车原理样机Fig.11 Prototype of the manned lunar rover

5.2 试验过程

1)J型工况

J型工况试验路径如图12所示。

如图13所示,车辆在0～8.5 s进行直线加速,此时质心侧偏角和横摆角速度都很小,左右两侧车轮转速匀速增加,在10 s时,车辆开始向右转向,此时车辆质心侧偏角达到-0.06,方向向右,横摆角速度最大达到-0.2,左右侧车轮产生转速差,到11 s时车辆开始向左进行J型转弯,质心侧偏角达到0.07并维持,横摆角速度达到0.25,到12.5 s时,J型转弯结束,车辆方向开始向右微调随后回正,质心侧偏角达到-0.04后回到0附近,横摆角速度到达-0.1后也回到0附近,车辆停止运动。由试验结果可以看出,车辆在11 s时进行J型转弯,质心侧偏角和横摆角速度符合预期,质心侧偏角在J型转弯时最大为0.07,横摆角速度最大值为0.25,车辆行驶较稳定。

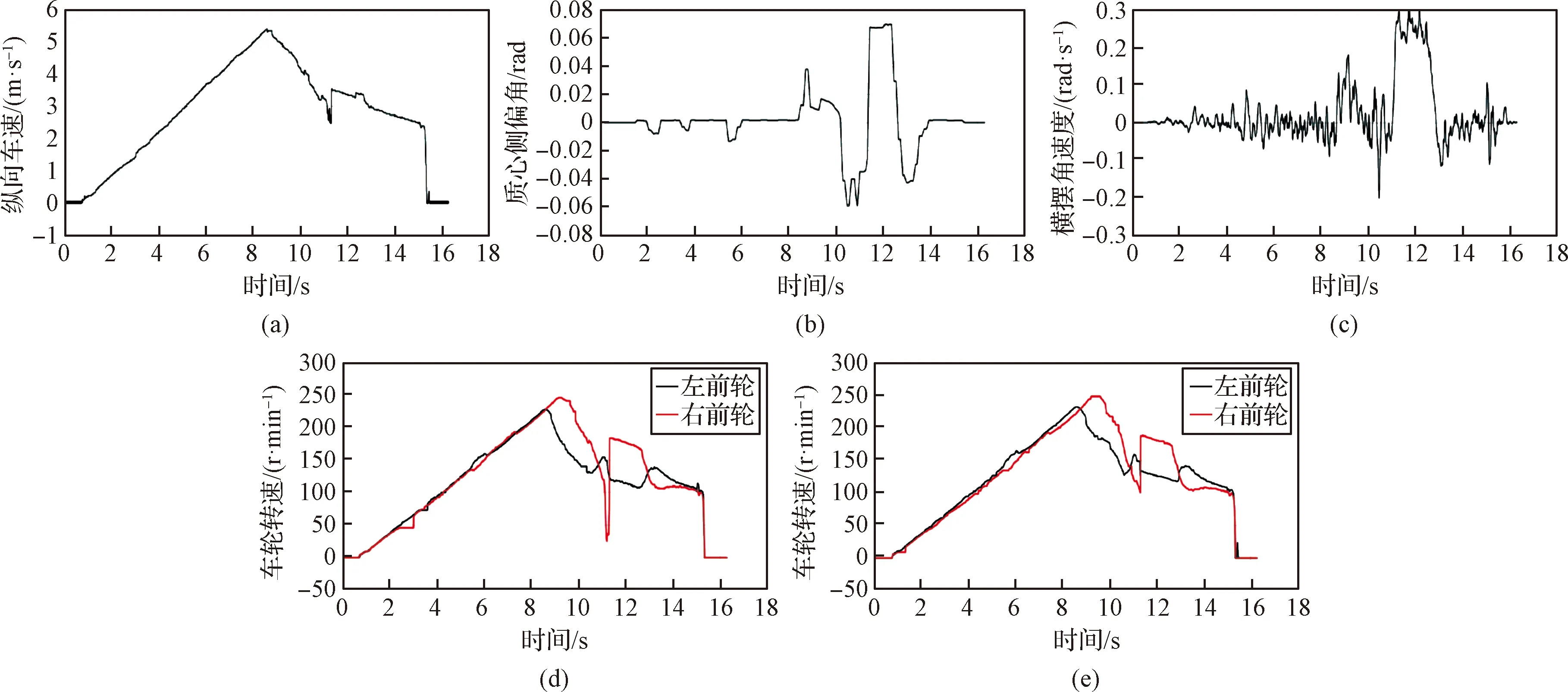
图13 J型工况试验结果Fig.13 Test results of J-type working path

2)对开路面

对开路面工况,路况设置为车辆从零加速,由良好路面直线驶入附着系数较低的潮湿金属板路面,如图14所示。

图14 对开工况试验路径Fig.14 Test path under split pavement

在对开路面行驶工况下(左侧附着系数高,右侧附着系数低),为了验证控制系统防滑功能有效性,分别在禁止驱动防滑功能和启动驱动防滑功能的条件下进行试验,结果如图15、图16所示。

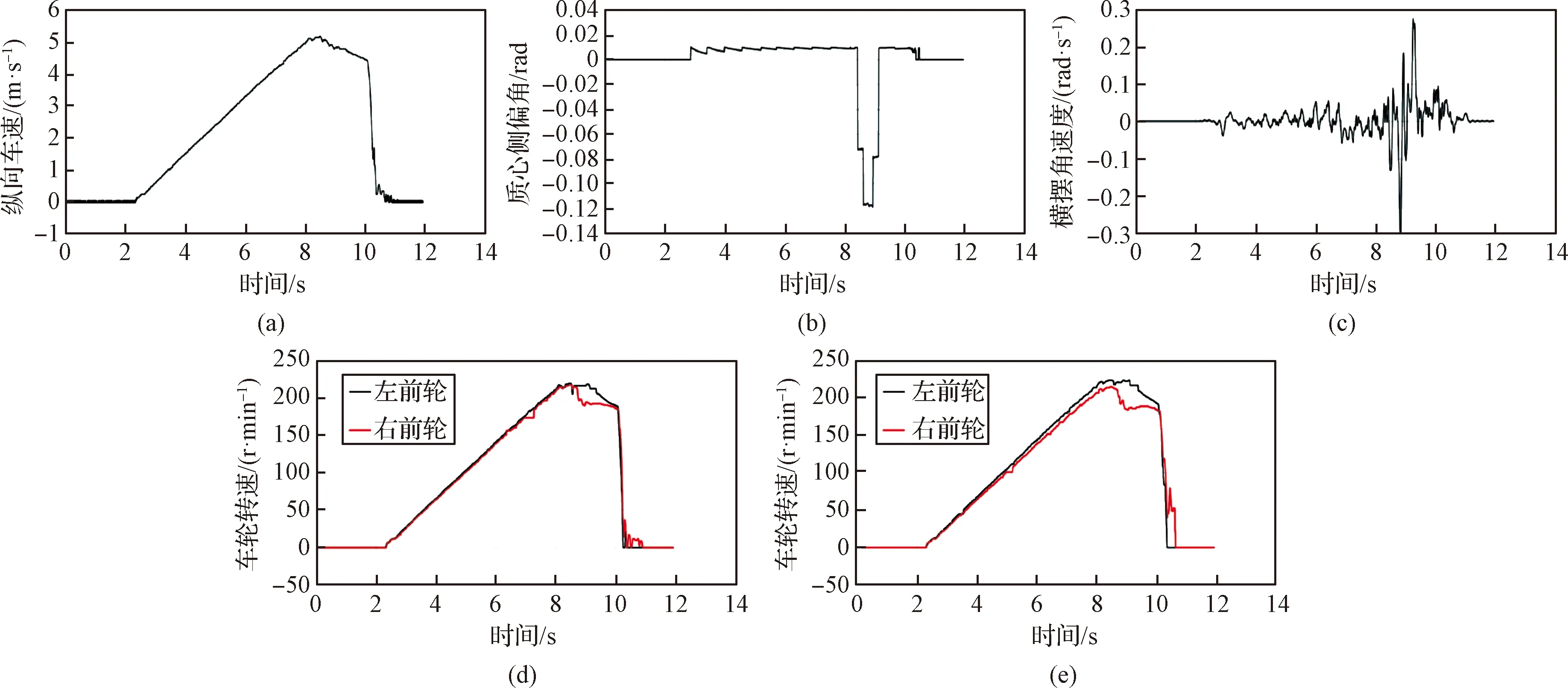
图15 对开路面无驱动防滑功能试验结果Fig.15 Test results without anti-slip control under split pavement

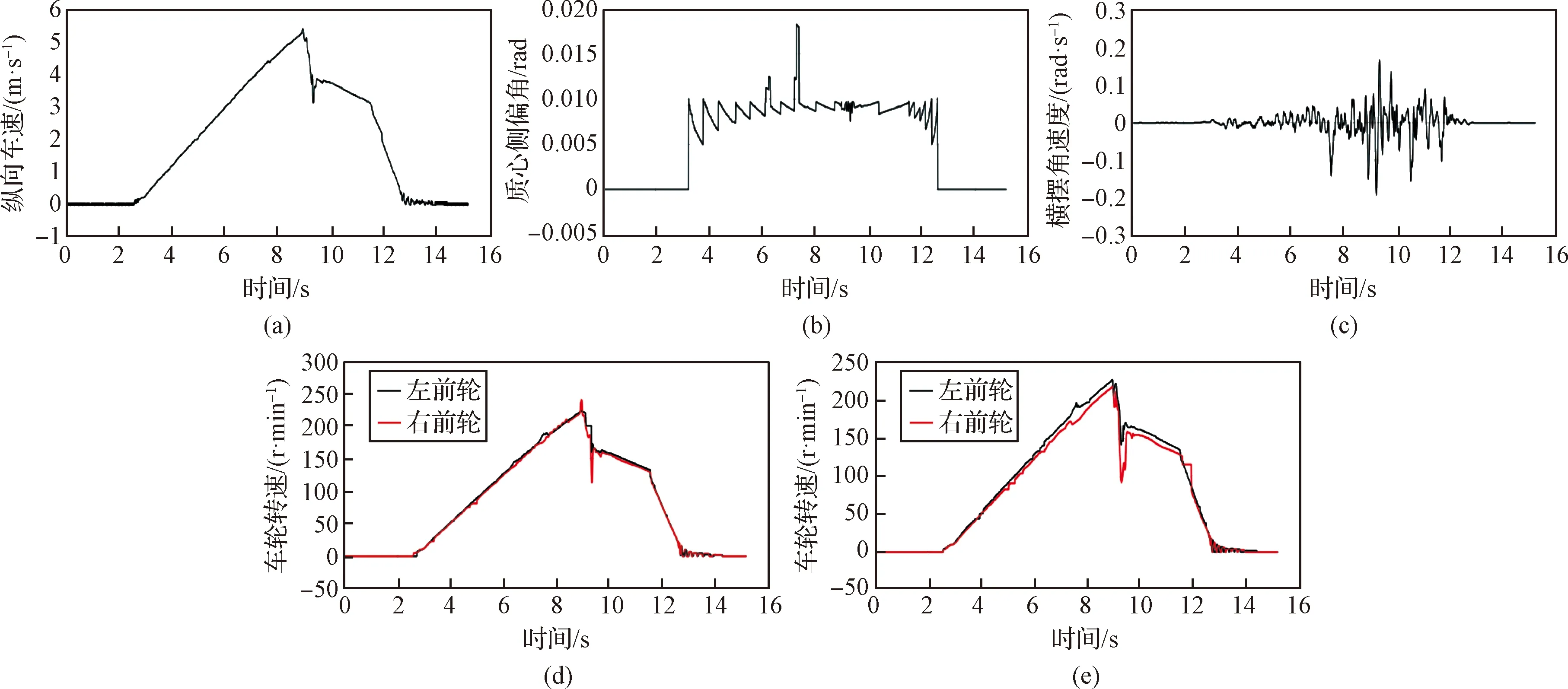
图16 对开路面有驱动防滑功能试验结果Fig.16 Test results within anti-slip control under split pavement

由图15可以看出,车辆在没有驱动防滑功能时通过对开路面,在0～8 s匀加速直线运动,车辆速度匀加速到5 m/s,此时质心侧偏角很小,维持在0.01附近,比较稳定,横摆角速度也比较小,在0附近波动,此时车辆两侧车轮转速基本一致,转速差很小,当车辆8.3 s通过对开路面时,右侧车轮通过附着系数较低的潮湿金属板路面,质心侧偏角突变到-0.12,横摆角速度也增大到了-0.3,此时车辆两侧车轮转速产生转速差,车辆发生明显右偏。

图16表明,车辆在驱动防滑模块的控制下通过对开路面时,在0～9 s时进行匀加速直线运动,此时车辆运动状态与无驱动防滑功能时运动状态基本一致,车速匀加速到5.5 m/s,车质心侧偏角比较小,维持在0.01附近,比较稳定,车横摆角速度保持在0附近,两侧车轮转速基本一致,转速差很小,当车在9 s驶入附着系数较低的潮湿金属板路面时,驱动防滑模块检测到右侧车轮滑移率增大,达到设定最大滑移率值,驱动防滑功能生效,降低输出电机转矩,电机转速下降,车速下降,车质心侧偏角未发生明显增大,依然维持在0.01附近,横摆角速度有一定程度增加,最大达到-0.2,总体相较于无驱动防滑功能时车辆驶入附着系数较低的潮湿金属板路面,横摆角速度有一定程度减少,车辆未发生明显右偏,说明驱动防滑功能控制效果良好。

特别说明的是,实车试验中的质心侧偏角、横摆角速度及车速信号等相较于仿真工况而言均存在一定的数据抖动。这是由于传感器本身性能特点造成的,尽管存在一定扰动,但并没有出现严重偏离真实范围的情况,没有干扰到整车控制策略的有效执行。

6 结 论

本文以载人月球车为研究对象,有针对性地设计了适用于车辆动力总成特点的操纵稳定性控制策略,结合月面行驶时存在的车辆易侧滑侧翻、车轮易过度滑转及腾空等风险,又进一步开展了策略优化设计。通过分层策略,将车辆运动控制的不确定性、非线性等问题集中于上层控制器,将约束条件下的转矩分配问题集中于下层控制器,分层控制结构使控制系统层次清晰、目标明确。之后进行了不同工况实车试验,试验结果表明,控制策略能够根据航天员的实时输入信号对车辆进行操纵稳定性控制,控制效果良好,整体载人车控制系统有较好的可靠性,达到了既定技术指标。