载人月球探测序列任务组合仿真设计与试验

王 华，吕纪远，李海阳

(1. 国防科技大学空天科学学院，长沙 410073；2. 空天任务智能规划与仿真湖南省重点实验室，长沙 410073；3. 中国航天员科研训练中心，北京 100094)

0 引 言

美国正在推进阿尔忒弥斯计划,采用基于地月空间站的飞行方案,以地月“门户”空间站为枢纽,支持载人月球探测任务以及未来载人火星探测任务,选定月球南极作为着陆区,建立月球基地[1-2]。

中国也在加紧载人月球探测研究论证,新一代载人运载火箭、新一代载人飞船的总体方案论证和关键技术攻关也在同步进行当中[3-4]。同时,国内又重新掀起了对载人登月近距离交会制导策略[5]、载人月球探测地月转移轨道设计方法[6-8]、载人月球软着陆GNC技术[9]、月面上升器起飞参数设计方法[10]等关键问题的研究热潮。这些研究表明中国已经逐步具备了载人登月的理论基础,实现载人登月的技术储备已经日臻完善。

目前,国内学者分别从航天器动力学建模、分系统仿真、飞行控制仿真与平行系统等方面开展了数字化仿真研究[11-15],但这些仿真系统与仿真应用捆绑过紧,通用性和可移植性不足,难以适应载人月球探测多个序列任务仿真的需要。本文以组合化思想采用1套仿真模型和1个仿真平台完成多个飞行任务仿真,根据4类载人月球探测序列任务特点,抽象出通用仿真模型,然后将仿真模型组合,形成具备4种任务仿真功能的仿真系统,并进行了载人月球序列任务仿真试验。

1 载人月球探测序列任务

基于地月空间站的方案是一种典型的载人月球探测模式[16-17]。基于稳妥可靠的任务宗旨,基于地月空间站开展的载人月球探测通常包含无人绕月飞行、地月空间站部署、载人环月飞行、载人登月飞行等多个序列任务。

1.1 无人绕月飞行

利用新一代运载火箭直接将载人飞船送入自由返回地月转移轨道,不执行近月制动,绕过月球后直接进入月地转移轨道。到达地球附近时,返回舱采用半弹道式再入大气层安全着陆。

1.2 地月空间站部署

采用新一代运载火箭将地月空间站送入地月转移轨道,到达近月点后制动进入环月轨道部署。

1.3 载人环月飞行

新一代运载火箭发射,将载人飞船送入自由返回地月转移轨道。到达近月点附近,载人飞船制动进入与地月空间站共面的环月轨道。载人飞船与空间站交会对接。返回时,载人飞船与空间站分离后加速进入月地转移轨道返回地球。

1.4 载人登月飞行

新一代运载火箭发射,将月面着陆器送入地月转移轨道,到达近月点制动进入环月轨道,与空间站交会对接。新一代运载火箭发射将载人飞船送入地月转移轨道,到达近月点制动进入环月轨道,与空间站交会对接。月面着陆器与空间站分离,完成环月轨道离轨,进入椭圆轨道,于近月点开始动力下降,完成接近、悬停、避障和减缓下降飞行,在月球表面软着陆。月面活动完成后,上升器起飞与空间站对接,航天员择机乘坐载人飞船返回地球。飞行过程如图1所示。

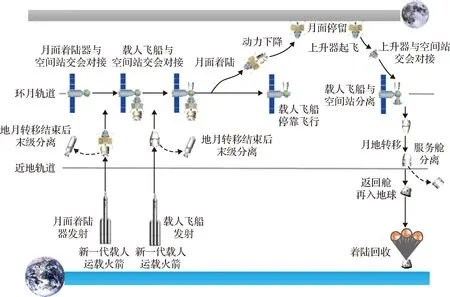
图1 载人登月飞行过程Fig.1 Flight profile of manned lunar landing

2 载人月球探测仿真模型

首先分析载人月球探测通用化仿真模型体系,然后重点介绍轨道动力学、地月转移规划和月地返回规划等模型。

2.1 通用化仿真模型体系

针对无人绕月、空间站部署、载人环月和载人登月4类飞行任务,传统仿真系统构建方法需要对这4类任务分别建立仿真模型,这不仅会大大增加人力物力成本,而且会导致系统拓展性差,难以适应载人月球探测飞行方案的变化。

从4类飞行任务出发,将载人飞船、月面着陆器等模型分解为子模型,提取子模型之间的共性信息,抽象得到载人月球探测13个通用模型,如图2所示。在抽象过程中,主要采用如下通用化路线:

图2 载人月球探测通用化模型体系Fig.2 Portable model architecture for manned lunar exploration

1)多任务模型通用化。将不同飞行任务中包含的相同飞行器模型抽象为一个飞行器模型,如将无人绕月、载人环月、载人登月中的载人飞船控制模型都抽象为“载人飞船GNC模型”。

2)多飞行器模型通用化。将不同飞行器包含的相同模型抽象为通用模型,如将载人飞船、月面着陆器、地月空间站中的动力学模型抽象为通用动力学模型,将地月空间站和月面着陆器地月转移规划都抽象为“一般地月转移规划”。

2.2 轨道动力学模型

载人月球探测飞行器需要在地球和月球之间飞行,考虑地球和月球的高精度引力以及各种摄动力的轨道动力学模型为

(1)

式中:m为飞行器质量;r为飞行器位置矢量;FE为飞行器所受的地球引力;FM为飞行器所受的月球引力;FN为飞行器所受的太阳和其他行星三体引力;FA为飞行器所受的大气阻力摄动;FSR为飞行器所受的太阳光压摄动;FT为飞行器所受的潮汐摄动。轨道动力学模型建立在地心J2000惯性系和月心J2000惯性系中,根据飞行阶段自动切换。

仿真中采用定步长与变步长结合计算轨道动力学模型,正常仿真时采用定步长Runge-Kutta 8阶算法,跳时仿真时采用变步长Runge-Kutta 89阶算法。

2.3 自由返回地月转移规划模型

基于地月空间站的载人月球探测序列任务,主要以环月轨道交会对接为关键环节展开,因此从近月段参数规划任务轨道,更有利于任务解耦[18]。本小节从双二体模型、近月伪参数和设计约束3个方面介绍自由返回地月转移规划模型。

2.3.1双二体建模

(2)

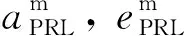
(3)

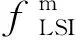
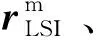
(4)

(5)

随后,地月转移入射点(TLI)到入口点的转移时间可以表示为

(6)

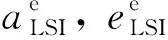
(7)

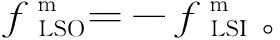
2.3.2规划参数设计

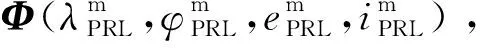
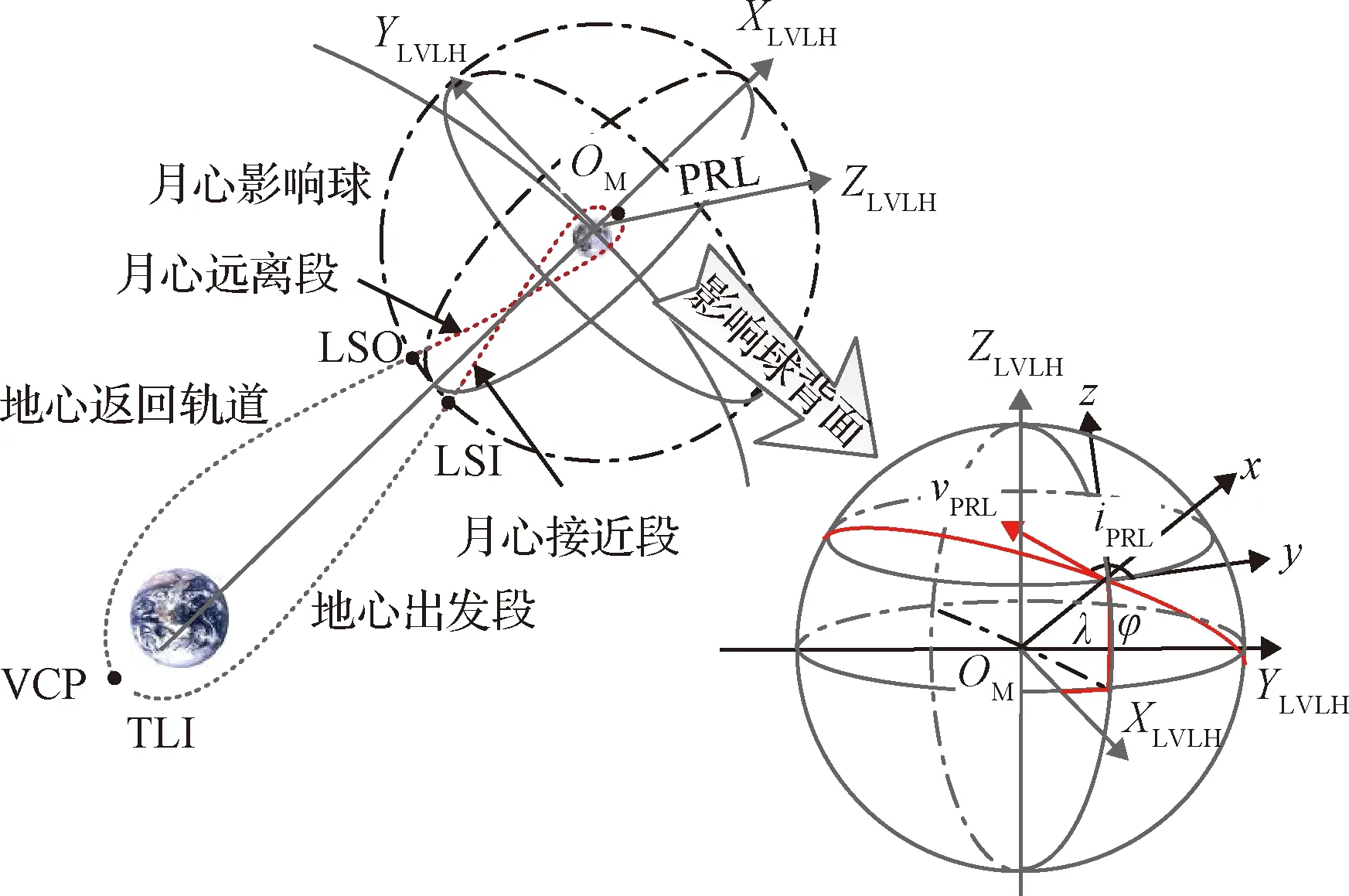
图3 近月点坐标系及近月伪参数示意图Fig.3 Diagram for perilune coordinate and pseudo-perilune parameters

(8)

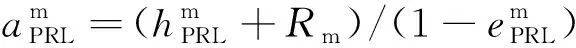
(9)

(10)

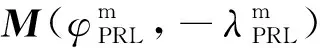
随后,按照圆锥曲线拼接法计算4段轨道的转移时间和轨道根数。

2.3.3规划设计约束

为了节省燃料,TLI点一般取地月转移轨道的近地点,地月转移轨道设计需考虑TLI点的高度和轨道倾角约束。

将进入大气层时刻作为飞行器再入时刻,飞行器再入时的速度与当地水平面的夹角作为再入角γ。为了保证过载、热流等条件的限制,再入角和真空近地点高度都需要满足一定范围。当给定大气高度时,利用二体理论可以建立再入角与VCP之间的联系。已知再入角γ与再入时刻的真近点角freen的关系为

(11)

式中:eLSO为LSO到地球返回段的轨道偏心率。真空近地点地心距rVCP与再入点地心距rreen的关系为

(12)

式中:hatmos为大气层高度;Re为地球半径。将式(11)等号两边平方,并利用上式替换其中的cosfreen和sinfreen,可得

(13)

利用上式可以计算出2个真空近地点解。由于地心返回段偏心率在0.96～1之间,因此存在1个大于地球半径的解和1个小于地球半径的解。只保留大于地球半径的解,即:

(14)

由此,当给定大气层高度和再入角,即可根据地心返回段的轨道偏心率,给出真空近地点高度的约束。

(15)

结合以上过程,可以迭代计算出满足约束条件(15)的近月伪参数初值。

2.4 一般地月转移规划模型

序列任务中载人飞船采用自由返回轨道进行地月转移,其他飞行器则采用一般转移轨道,这两类轨道设计约束不同。自由返回设计需要在近月段进行多次脉冲机动来调整环月轨道面。而一般转移轨道的设计更为灵活,近月点处的轨道面参数可以根据实际需要来确定。

一般地月转移轨道规划问题的约束为出发端的高度hLEO和倾角iLEO,以及近月段的倾角iPRL和升交点赤经ΩPRL,可以表示为

(16)

若考虑一般月地返回轨道设计,仅考虑返回轨道倾角约束和真空近地点高度约束,可按式(14)计算。

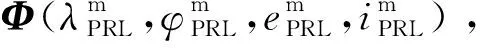
2)由上述确定初始轨道参数以及转移时间和约束,进行初始的多步迭代,明确一般转移轨道初值。

3)根据轨道设计初值和高精度轨道模型,采用二分法迭代插值,将轨道外推至VCP或TLI。

4)将高精度结果与设计约束进行对比,利用基于梯度的数值计算方法迭代计算出满足约束条件的近月伪参数结果。

2.5 月地返回规划模型

对于飞行约3天的月地返回轨道而言,定点返回地球某着陆场存在经、纬度2个匹配过程。

2.5.1纬度匹配

月球公转白道面相对赤道面夹角在每个默冬周期(约18.6年)中从18°18′到28°26′变化一次,如果忽略月心段轨道对整个月地定点返回轨道面的影响,则月地定点返回时刻的月球赤纬是影响返回地球着陆场纬度的主导因素。再参考月球拉普拉斯影响球理论,估算出月心段轨道可对整个月地返回轨道面产生约10°影响。总体而言,月地返回时刻月球赤纬幅值决定返回轨道再入点纬度。

2.5.2经度匹配

在惯性空间中,地球自转和月球公转同方向,约25小时月球扫过地表一周。待月面着陆器完成航天员、月壤等转移过程后,预留25小时调整匹配地球着陆场经度即可。

月地定点返回轨道求解方法与一般转移轨道类似,不再赘述。

2.6 月球转出规划模型

月地定点返回轨道与停泊轨道不同面,一般采用三脉冲月心大椭圆轨道来调整空间站轨道面与月地返回轨道面差异,3次近月脉冲时刻需要在25小时内迭代调整再入点时刻,用来匹配着陆场经度。第1次近月脉冲施加Δv1将飞船加速进入月心大椭圆轨道(LIO1),在目标轨道面与当前轨道面交线处点B进行第2次脉冲施加Δv2调整轨道面和近月点的高度,形成与返回轨道共面的月地转移轨道(LIO2),待再次返回近月点时施加第3次脉冲Δv3进入月地转移轨道(LIO3)。

(17)

(18)

式中:fLIO2为交线与拱线的夹角;uB为LIO2轨道上B点的纬度幅角,范围为[-π,π]。第2次改变异面差的脉冲在LIO2在B处LVLH坐标系下的分量为

(19)

约束B点为LIO1远拱点,则面内变轨的脉冲为

(20)

式中:rLDO为空间站停泊轨道(LDO)的轨道半径;rB为LIO1远拱点半径。第2次脉冲为

(21)

Δv1和Δv3均为切向机动,具体过程不再赘述。

3 载人月球探测仿真系统设计

3.1 仿真平台

载人月球探测序列任务的飞行流程各不相同,按照传统仿真系统设计,需要构建多组模型和多套仿真系统,这将导致仿真系统灵活性大大降低。针对以上问题,探索只采用1组模型和1个平台,通过模型组合实现多个序列任务的飞行流程仿真。

3.1.1仿真平台架构

国防科技大学与载人航天总体研究论证中心联合研制了dSIM仿真平台,已经成功应用于中国天宫一号、天宫二号和空间站任务联合仿真[19-20],dSIM仿真平台架构如图4所示。

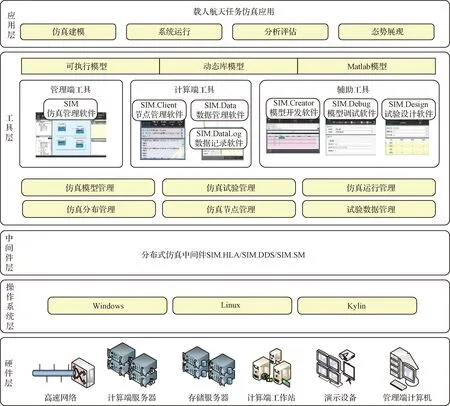
图4 dSIM仿真平台架构Fig.4 Framework of dSIM simulation platform

分布式仿真平台dSIM由应用层、工具层、中间件层、操作系统层和硬件层5层组成。应用层针对载人月球探测任务仿真等特定任务开发具体仿真应用,其他层构成具有可扩展性的通用仿真运行环境。为了在不同操作系统、不同仿真标准间达到仿真模型接口完全一致,dSIM在操作系统层和工具层之间,增加了中间件层来保证仿真模型可移植性。工具层提供管理端、计算端和辅助3类工具,包括仿真管理SIM、节点管理SIM.Client、数据管理SIM.Data、模型开发SIM.Creator、模型调试SIM.Debug等软件。

3.1.2仿真平台关键技术

为了适应无人绕月飞行、地月空间站部署、载人环月飞行、载人登月飞行4类序列任务仿真需求,降低模型开发工作量,提高模型可移植性,dSIM平台采用以下关键技术。

1)分布式仿真中间件技术

采用分布式仿真中间件将仿真模型与仿真框架完全分离,解除仿真模型与仿真平台的耦合,规范仿真模型和底层通信各自的接口,使得仿真模型和底层通信可以独立发展。仿真模型不再区分集中式或分布式,分布式仿真时也不再区分底层通信协议,可以是HLA,也可以是DDS等。

为了提高仿真性能,分布式仿真中间件还采用了多层交互机制,如图5所示。在同一台计算节点上的模型之间采用共享内存交互机制,在不同计算节点之间的模型采用HLA交互机制,特别适合毫秒级高频与分钟甚至小时级低频交互混合仿真的需求。载人月球探测仿真中飞船等飞行器内部动力学和GNC模型之间采用毫秒级交互,飞船和着陆器等飞行器之间采用秒级交互。

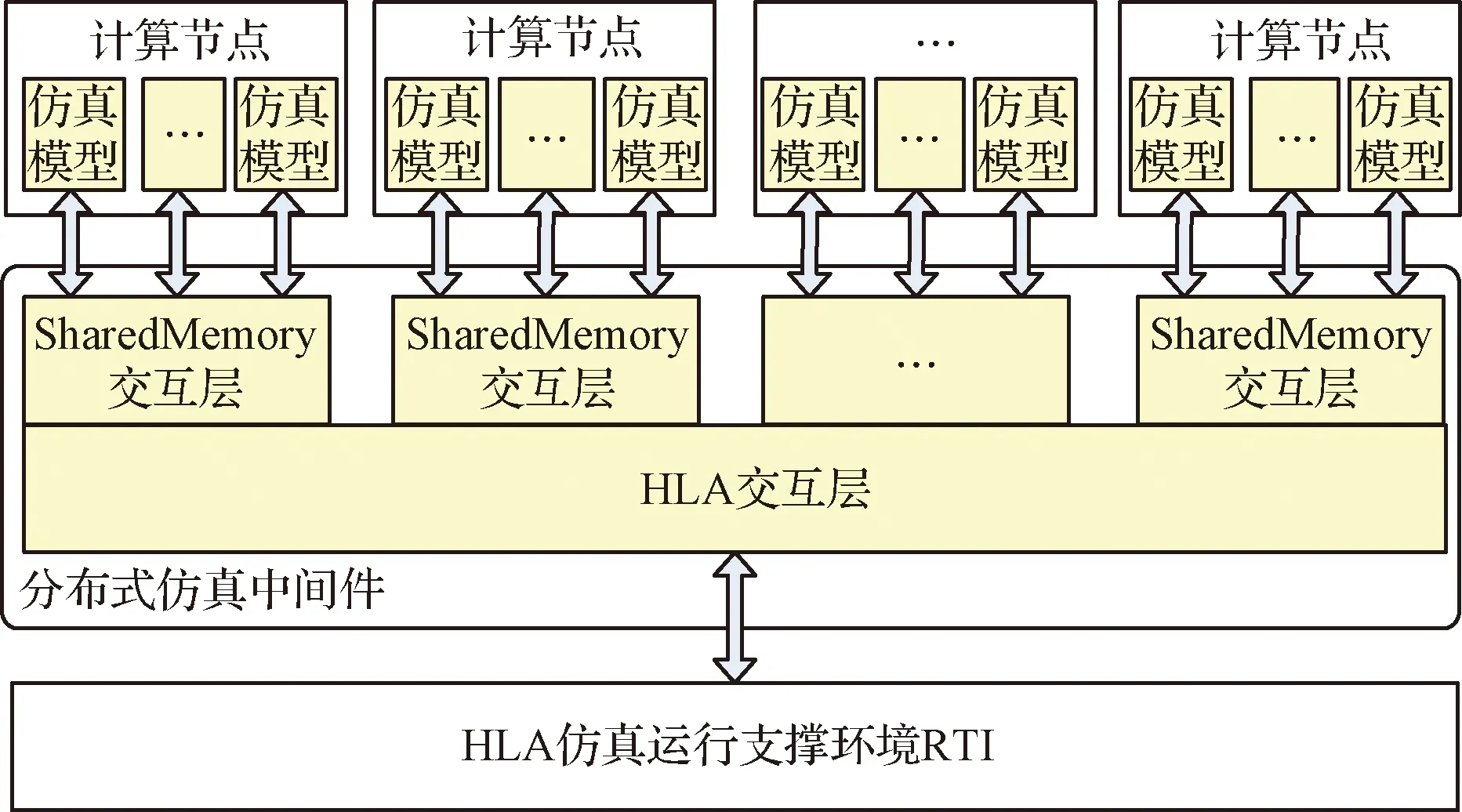
图5 分布式仿真中间件原理图Fig.5 Schematic diagram of the distributed simulation middleware

2)标准化模型规范

dSIM仿真模型可以看作一个具有输入输出端口的系统,其形式化描述可表示为六元组:

M=

(22)

式中:t是时间;X是输入变量;S是系统状态变量;Y是输出变量;F(t, Δt,X,S)是状态转移函数;G(t,X,S)是输出函数。

仿真模型遵循“描述与实现分离”原则,主要的仿真模型描述信息见表1。dSIM允许存在多种不同形式的模型,包括可执行模型、动态库模型、Simulink模型等,其中可执行模型的标准消息见表2。

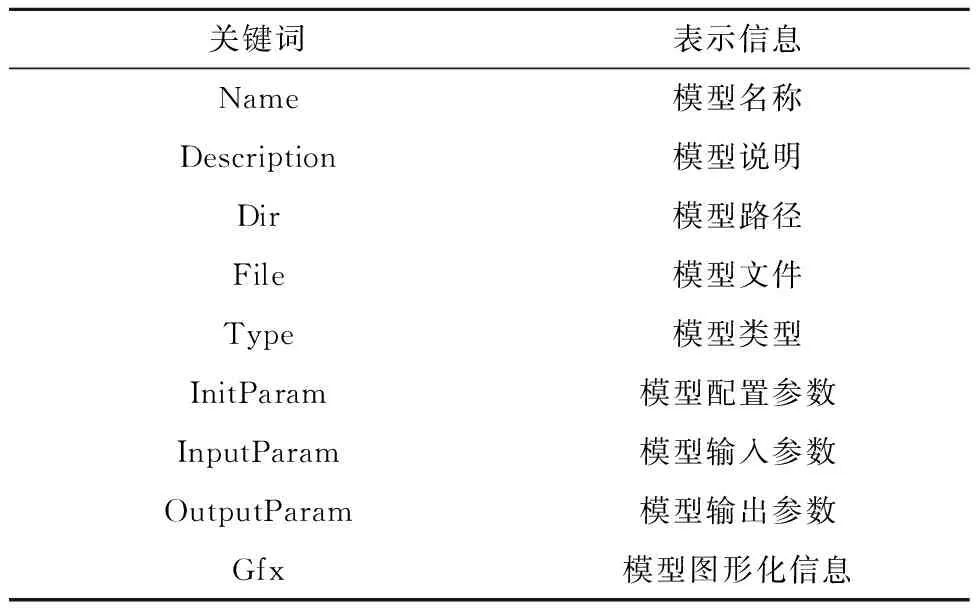
表1 dSIM仿真模型描述的关键字Table 1 Keywords to describe dSIM simulation model

表2 可执行模型消息Table 2 Message of executable model

3)可视化模型组合技术

dSIM利用可视化工具将可组合模型进行组装,其具有以下特点:①仿真模型可视化;②组合关系可视化,通过仿真模型图形端口之间的连线建立模型之间的交互关系;③模型组合零编程,对图形的操作完全替代了繁琐的手工编程。

3.2 模型组合

以相关研制部门的已有模型为基础,构建了可执行形式的仿真模型软件,利用这些仿真模型软件在dSIM仿真平台上可以灵活组合形成具备无人绕月飞行、地月空间站部署、载人环月飞行、载人登月飞行4种仿真功能的仿真系统。考虑到仿真重点支持载人探月任务前期论证,对任务规划、轨道建立了高精度模型,采用SQP算法优化求解,对测控通信则建立了简化模型。

4种仿真功能共用1个平台和1套模型,通过仿真模型的组合实现4类飞行任务,4种仿真功能包含的仿真模型见表3,其中,最复杂的载人登月飞行仿真功能的系统组成如图6所示。

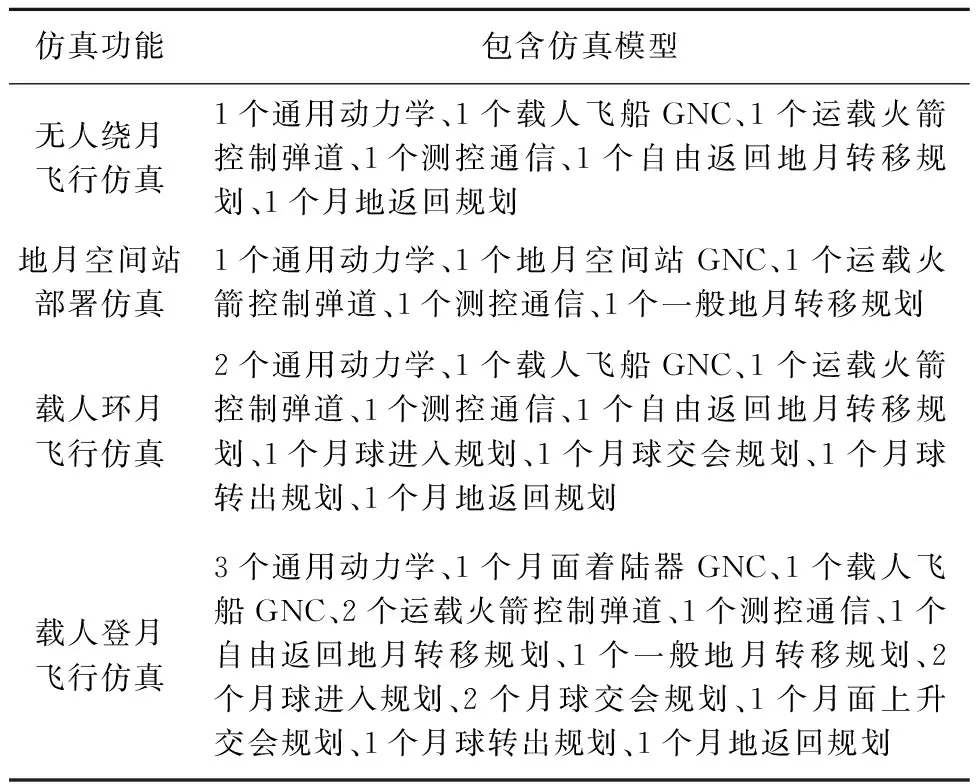
表3 4个仿真功能包含的可组合仿真模型Table 3 Composable models in the four simulation scenarios

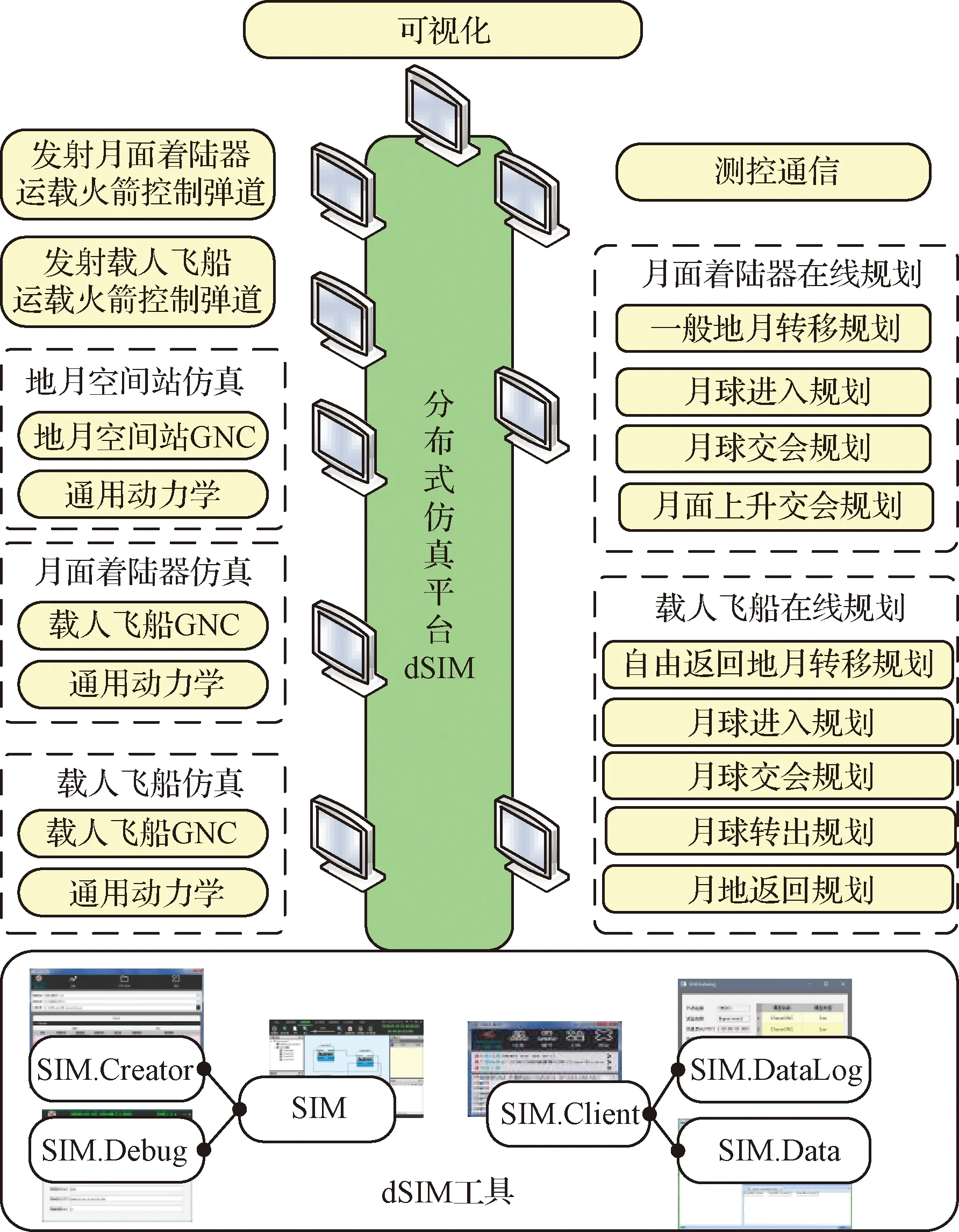
图6 载人登月飞行仿真功能组成Fig.6 Composition of the simulation scenario for manned lunar landing

载人登月飞行仿真功能包括发射月面着陆器的运载火箭控制弹道、地月空间站仿真、月面着陆器仿真、载人飞船仿真等9个节点,每个节点上又部署多个模型软件,如地月空间站仿真节点上部署地月空间站GNC、通用动力学2个模型软件。仿真系统采用多帧速模式,在计算机节点内部采用20 ms仿真步长,计算机节点之间采用1 s仿真步长。

4 仿真试验

利用通用模型组合形成的仿真系统分别进行仿真试验,下面对无人绕月飞行和载人登月飞行仿真试验进行介绍。

4.1 无人绕月飞行仿真试验

无人绕月飞行规划中重点关注发射弹道与转移轨道的衔接。完成离线规划后,在dSIM平台上对无人绕月飞行的运载火箭进行配置,然后进行仿真,得到无人绕月任务运载火箭的发射弹道仿真结果如图7～8所示,轨道仿真结果见表4。

表4 无人绕月轨道仿真结果Table 4 Trajectory results for unmanned lunar flyby

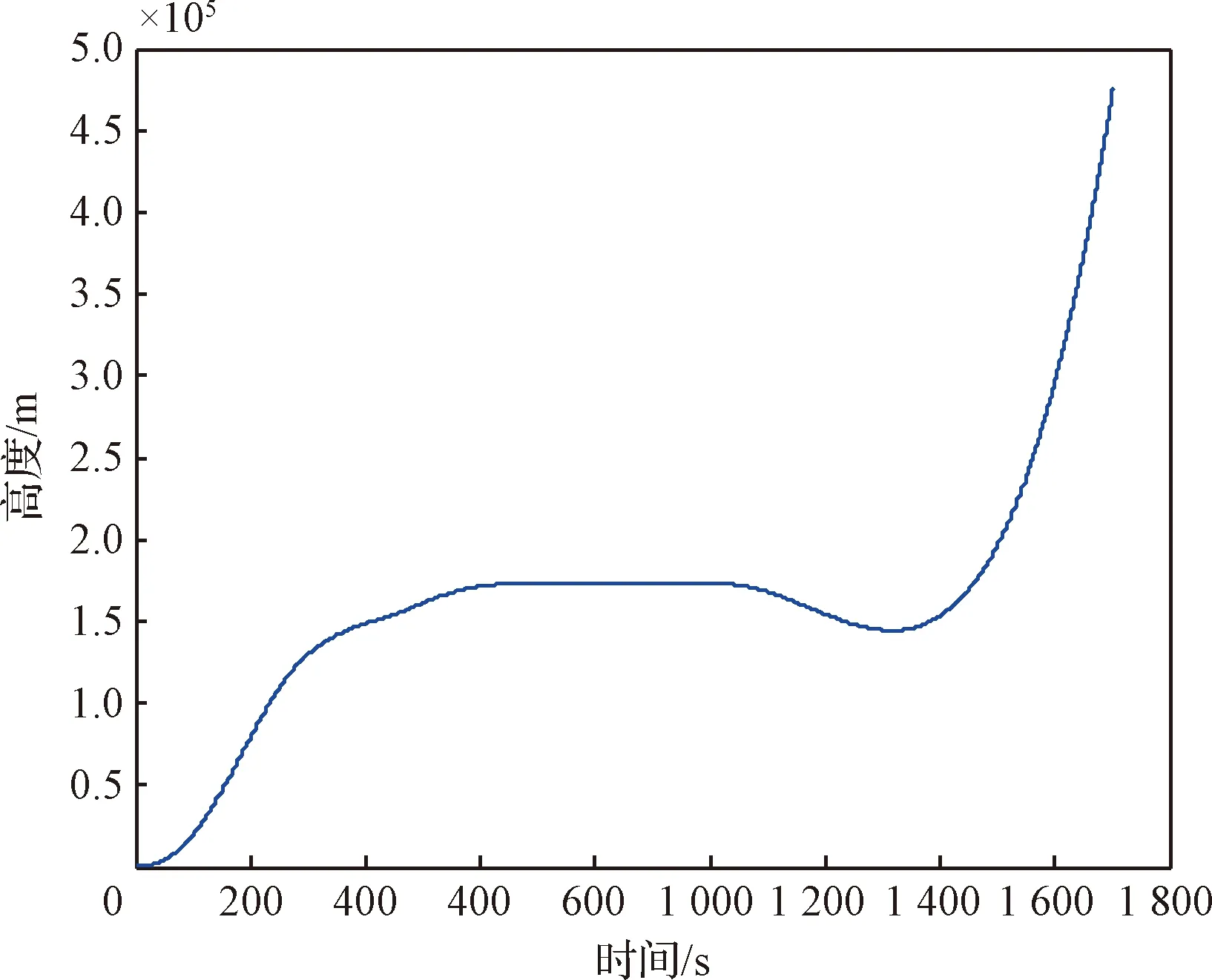
图7 无人绕月飞行运载火箭高度-时间曲线Fig.7 Curves of height versus time of the launch vehicle for unmanned lunar flyby

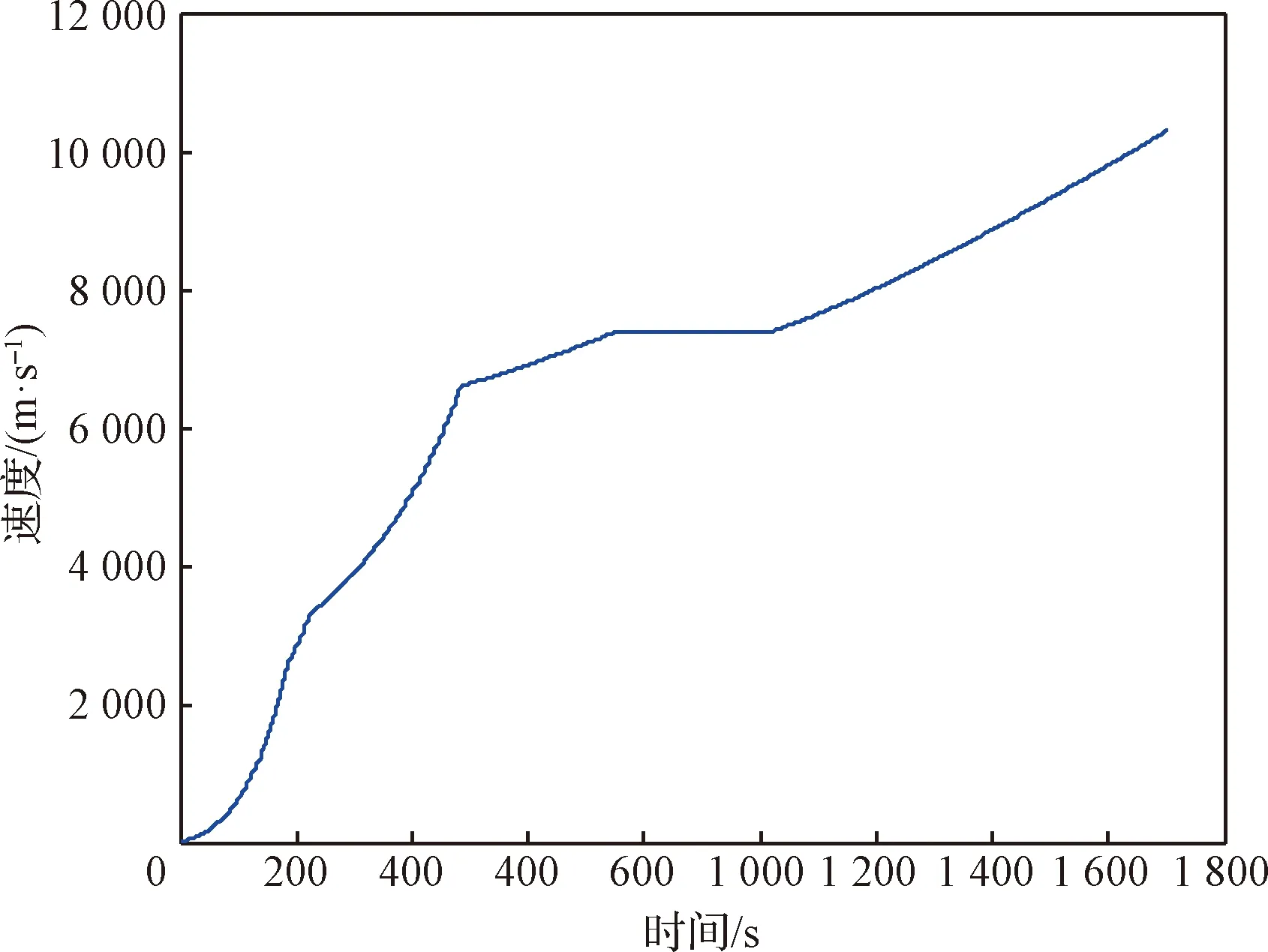
图8 无人绕月飞行运载火箭速度-时间曲线Fig.8 Curves of velocity versus time of the launch vehicle for unmanned lunar flyby

4.2 载人登月飞行仿真试验

载人登月飞行仿真试验输入参数主要包括时间设计参数、空间站停泊轨道(LDO)、地月转移轨道地心段(LTO)约束参数,仿真得到月面着陆器轨道结果见表5,仿真视景如图9所示。

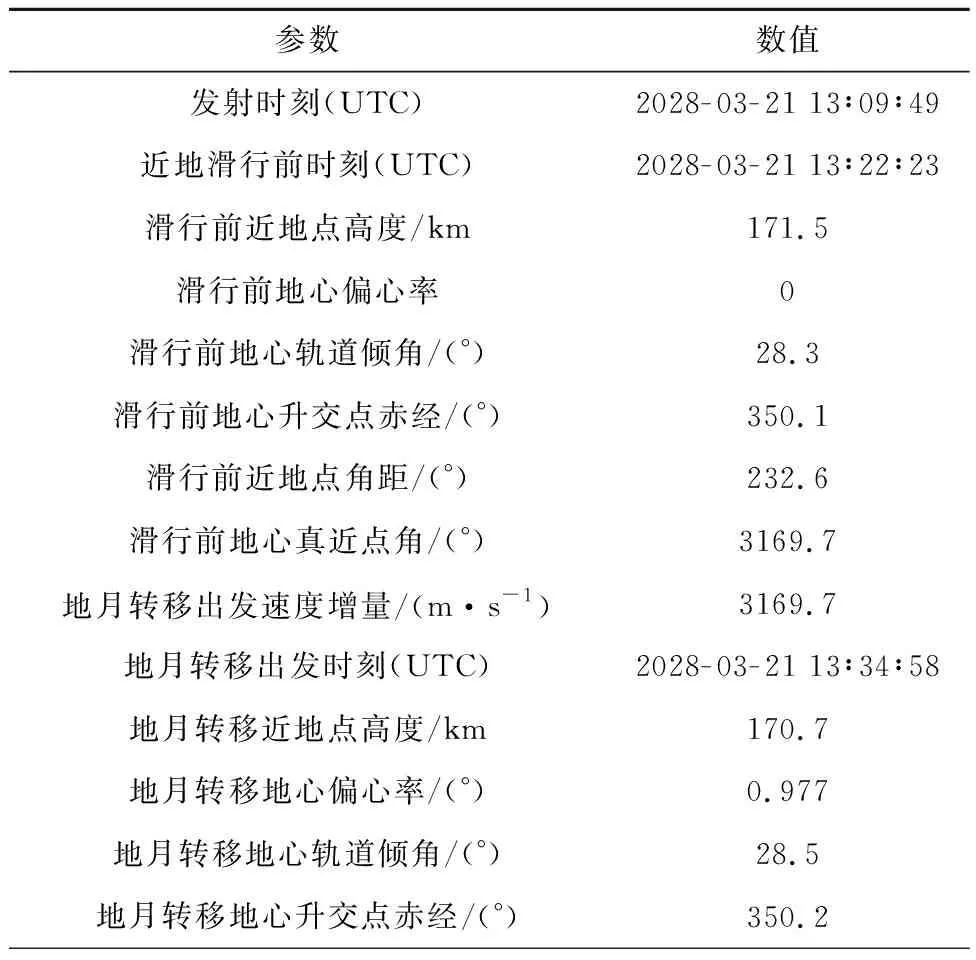
表5 月面着陆器标称任务轨道仿真结果Table 5 Simulation results of the nominal mission trajectory of the lunar lander

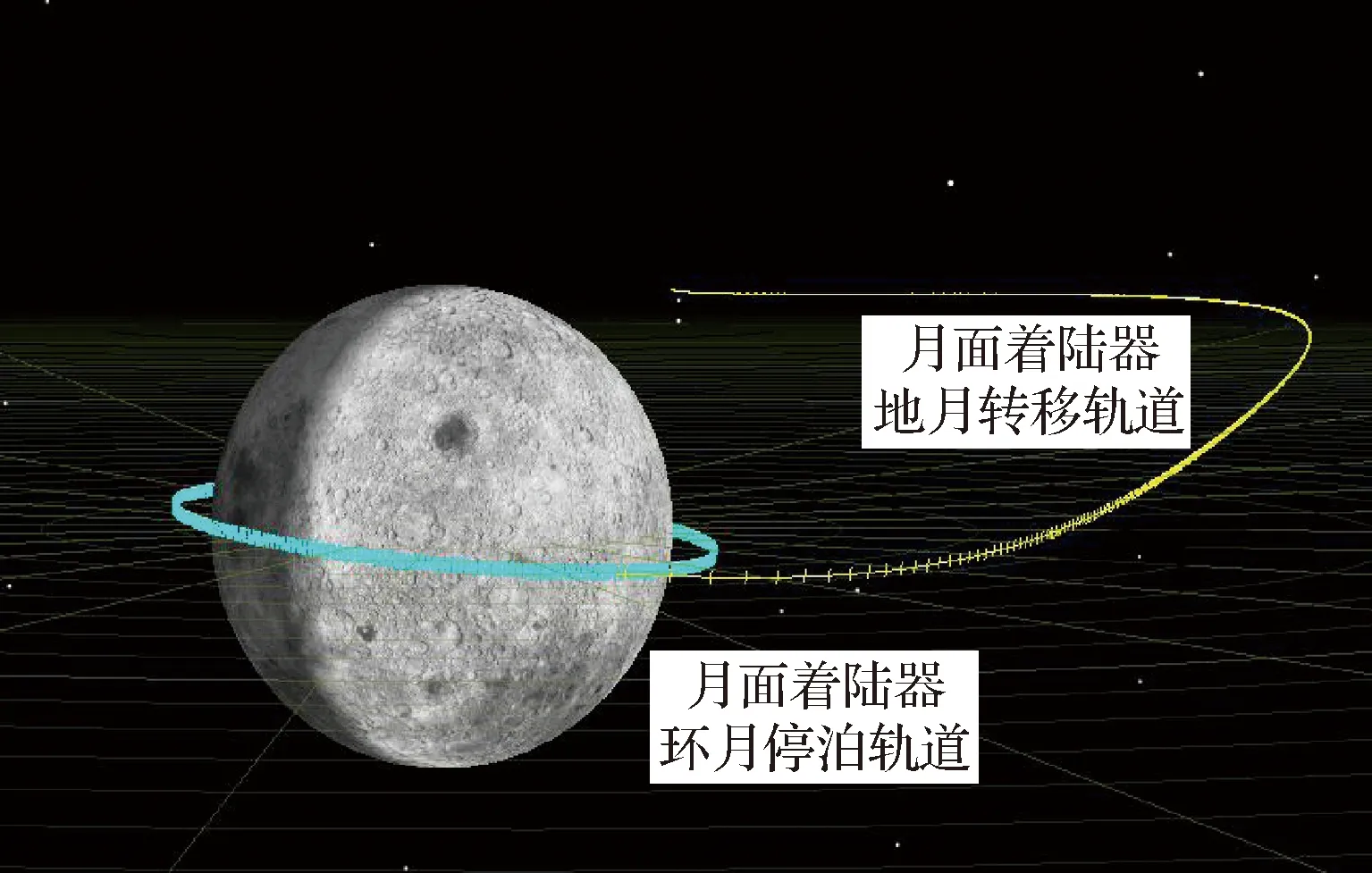
图9 月面着陆器地月转移和环月停泊轨道Fig.9 Trajectory of Earth-Moon transfer and circumlunar parking orbit of the lunar lander

空间站部署在高度约200 km、倾角约159°的月球近圆轨道上。新一代载人飞船任务持续时间约为15天,发射入轨点数据由模型软件迭代获得,中途修正、月面下降与上升轨道,采用速度增量的预留模式。月面着陆器与载人飞船的第1次交会对接,采用四脉冲优化方式给出。仿真得到的载人飞船标称任务轨道结果见表6～10,仿真视景如图10～11所示。

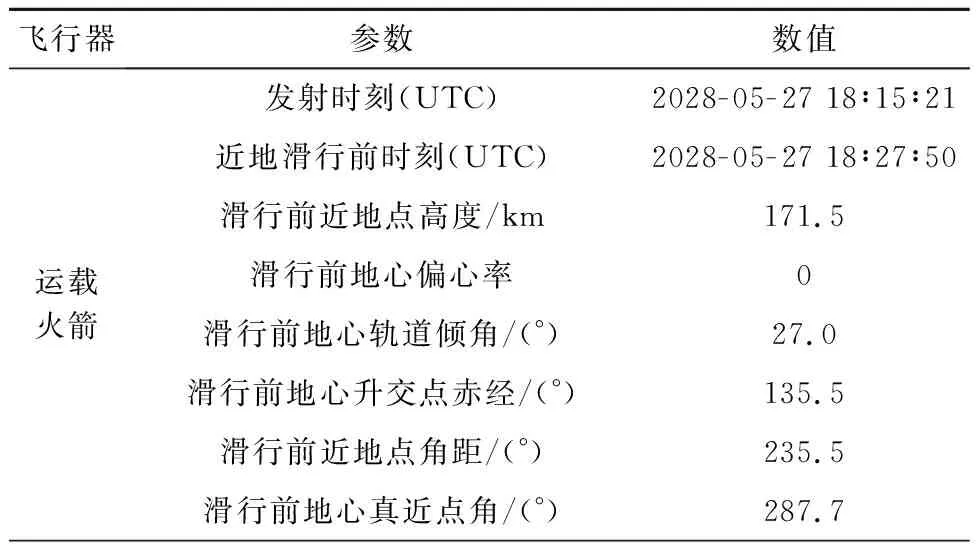
表6 载人飞船发射与地月转移仿真结果Table 6 Simulation results of launch and Earth-Moon transfer of the manned spacecraft

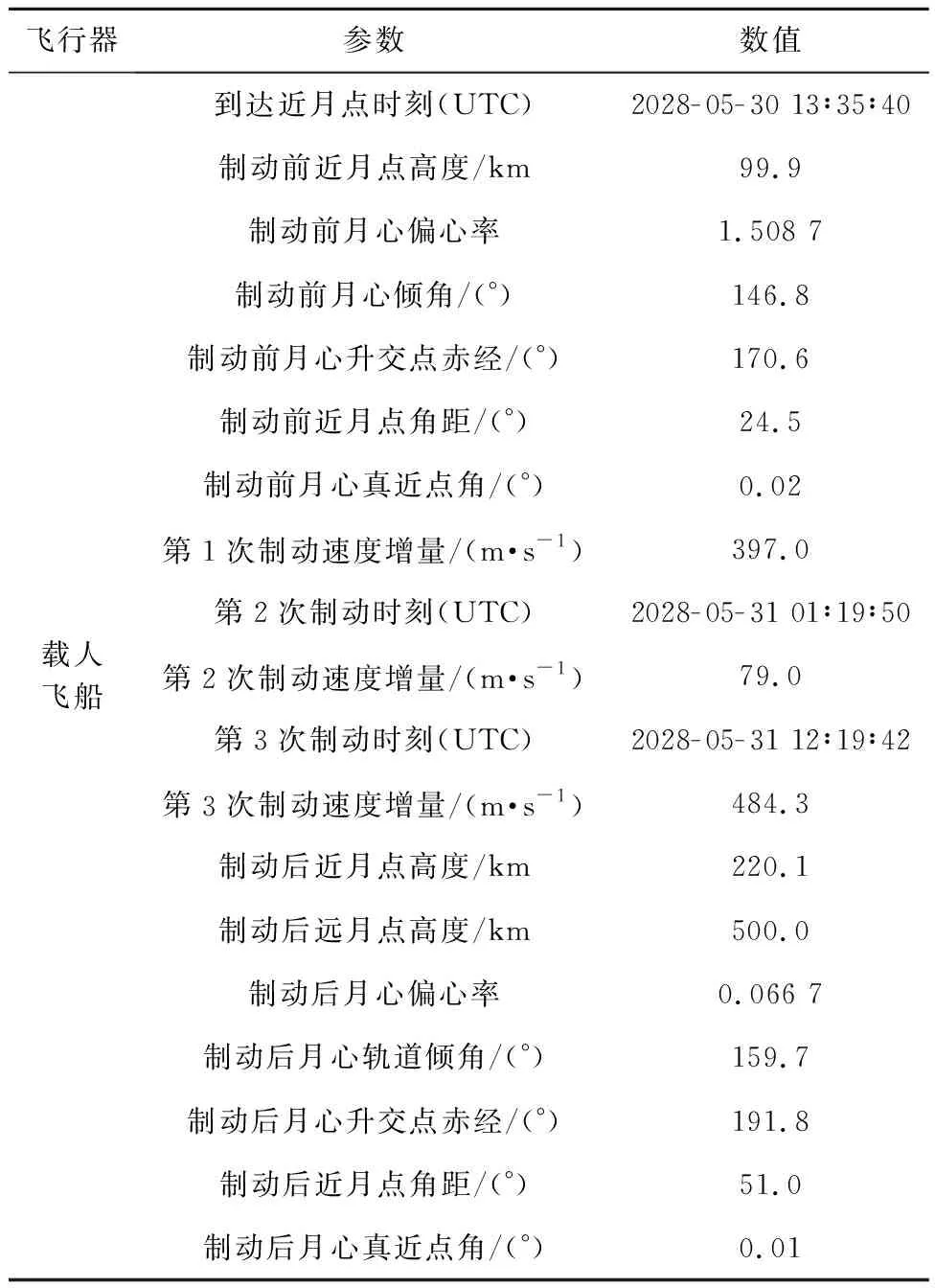
表7 载人飞船三脉冲月球进入仿真结果Table 7 Simulation results of three-pulse lunar orbit insertion of the manned spacecraft

表8 载人飞船月球轨道交会仿真结果Table 8 Simulation results of lunar orbit rendezvous of the manned spacecraft

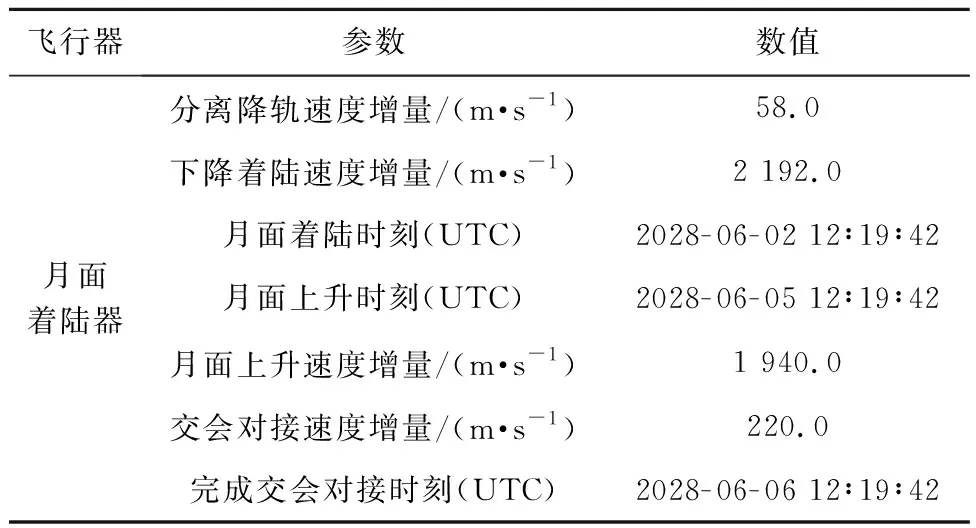
表9 月面着陆器下降与上升仿真结果Table 9 Simulation results of descent and ascent of the lunar lander

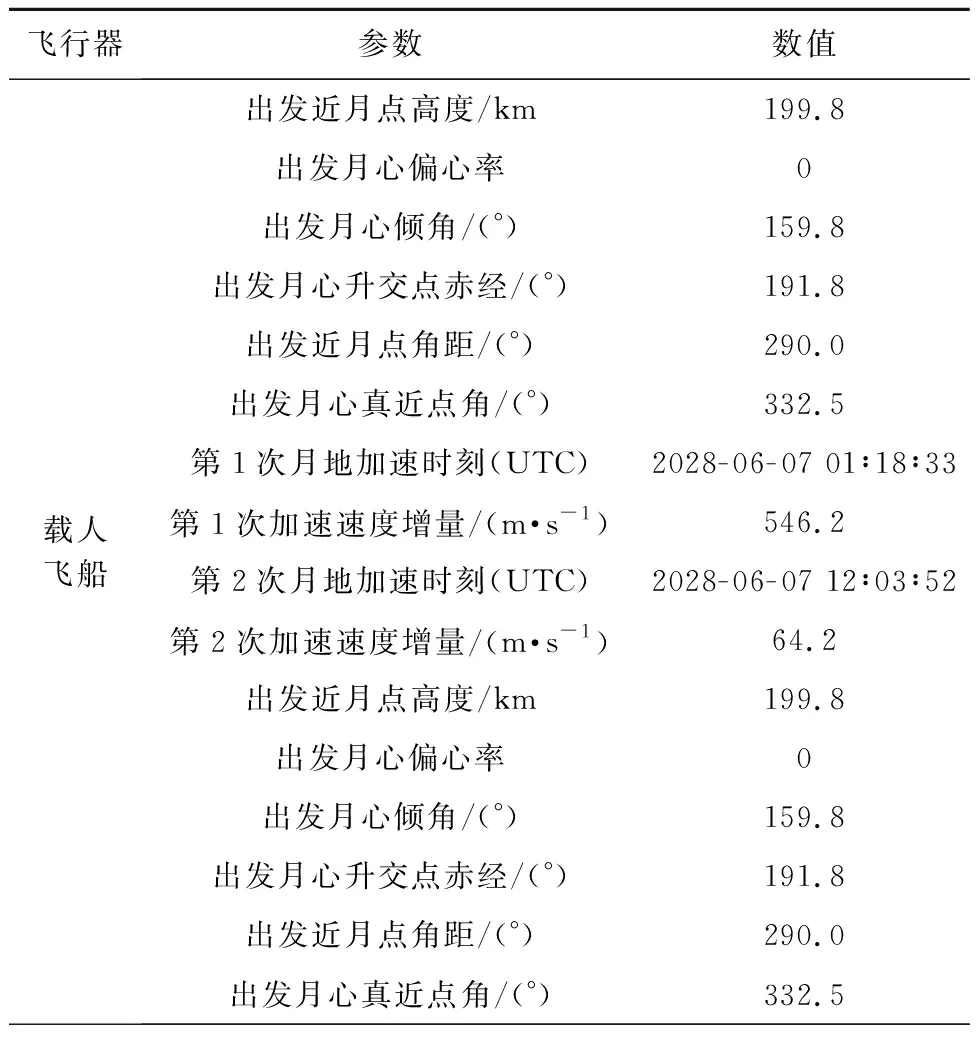
表10 载人飞船月地返回仿真结果Table 10 Simulation results of Moon-Earth maneuver of the manned spacecraft

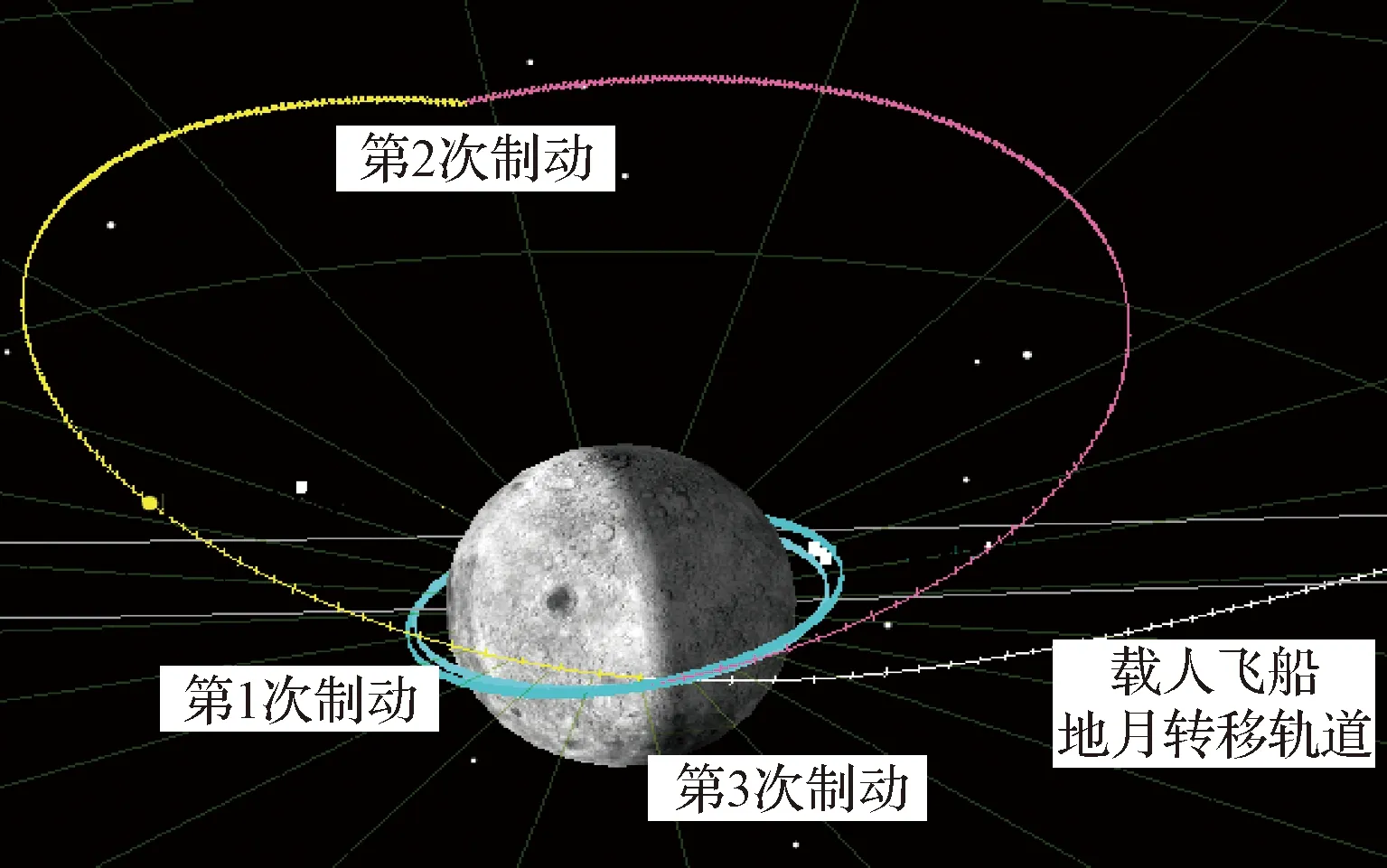
图10 载人飞船地月转移轨道结果Fig.10 Trajectory of lunar orbit insertion of the manned spacecraft

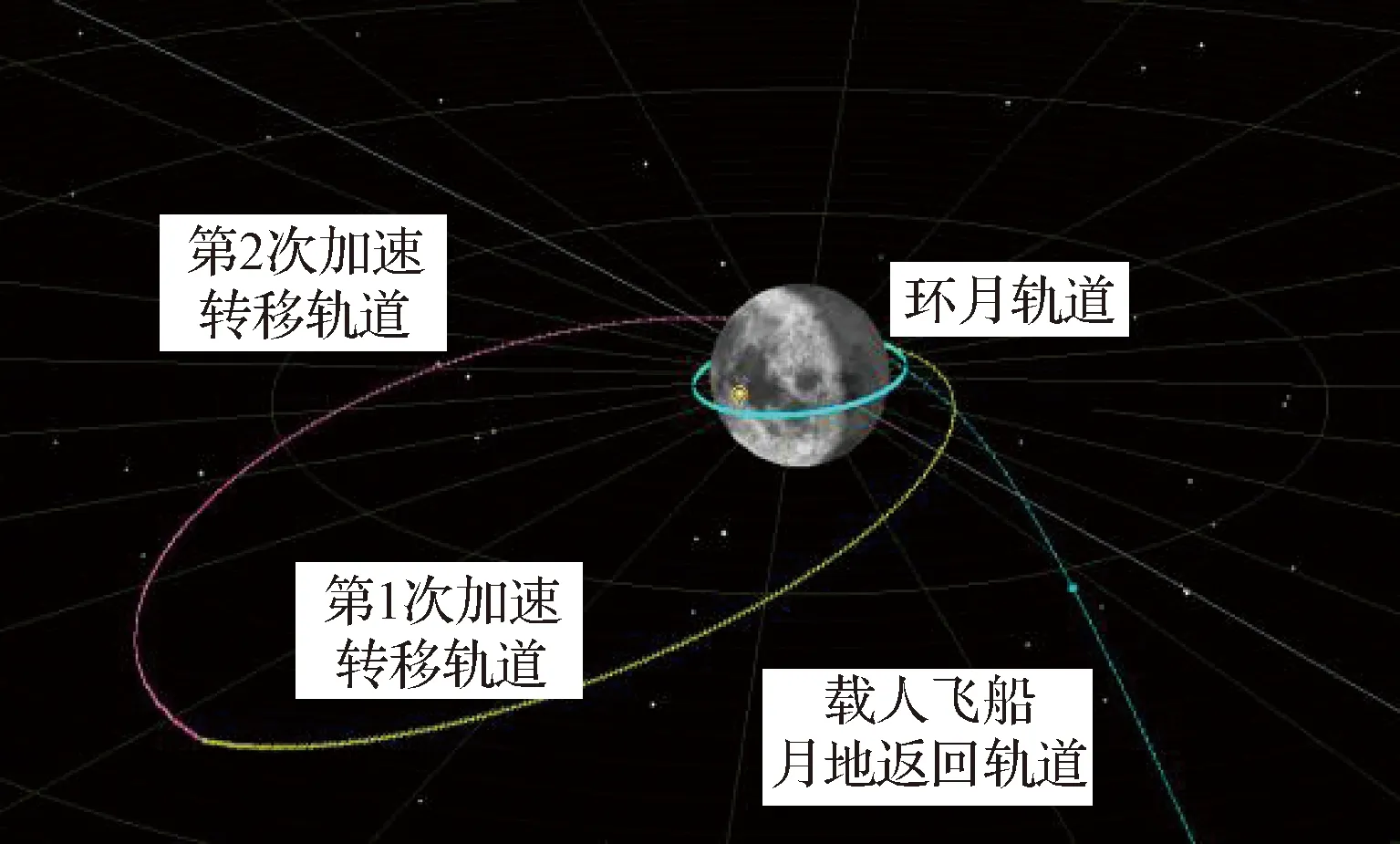
图11 载人飞船三脉冲月地加速轨道结果Fig.11 Trajectory of three-impulse Moon-Earth maneuver of the manned spacecraft

5 结 论

对于基于地月空间站的载人月球探测系列任务,本文利用组合仿真思想,按照仿真模型通用化思想将无人绕月飞行、地月空间站部署、载人环月飞行、载人登月飞行4类序列任务抽象为13个通用模型,设计了标准化组合化的仿真平台dSIM,将通用模型组合为具备4种功能的仿真系统,进行了仿真试验。文中给出的仿真试验结果说明了该方法的有效性。该方法可为未来载人月球探测系列复杂飞行任务仿真提供参考。