载人月球探测任务转移轨道及月面着陆区评估分析

丁百慧，杨 彬，秦 政，李 爽

(1. 南京航空航天大学航天学院，南京 211106；2. 中国航天员科研训练中心，北京 100094)

0 引 言

月球是地球的天然卫星,蕴藏着丰富的自然资源,具有巨大的军事价值。载人月球探测是开发月球自然资源掌控其战略地位的重要手段[1-2]。载人月球探测月面着陆区直接影响工程任务实施与科学研究成果,着陆区的选择涉及到科学研究与应用价值分析、飞行器约束条件分析、月面驻留与活动支持能力分析等关键环节。月面着陆区遴选工作需由科学需求牵引,首先提出最具科学价值月面备选着陆区;在此基础上,论证分析工程代价约束,进行飞行轨迹设计,并逐一对备选着陆区进行综合代价评估分析[3-4]。因此,高效可靠的飞行轨迹设计与综合代价评估分析方法是载人月球探测任务开展的前提。

阿波罗计划是迄今首例成功的载人登月任务,1966年至1972年间先后有12名航天员登上月球[5]。阿波罗计划采用的“人货混运、月球交会”的模式对火箭运载能力要求极高,且安全性和任务灵活性不足[6-7]。因此,现已公布的各国未来载人登月计划均采用“人货分运、多次交会”模式,充分利用成熟的大型运载火箭和飞船,节省任务成本,强调实用性和可靠性[8-9]。不论是阿波罗计划的“人货混运”还是未来的“人货分运”模式,整个任务飞行阶段包括发射段、近地停泊段、地月转移段、环月飞行段、月面下降、月面上升段及月地转移段。其中,发射段和月面下降、月面上升段分别由运载火箭和登月舱执行。本文的转移轨迹设计和分析主要围绕载人飞船和着陆器参与的地月转移段和月地转移段展开。

地月往返转移段是连接近地轨道和环月停泊轨道的轨迹,期间航天器受到地球和月球引力的共同作用,属于典型的三体问题[10]。为提升任务的安全性,载人地月转移段通常采用自由返回轨道,即载人飞船借助月球引力辅助作用在不施加额外机动的情况下返回地球[11]。因此,地月转移轨道设计本质上是高精度地月自由返回轨道设计问题。黄文德等[12]基于双二体模型采用圆锥曲线拼接法完成了自由返回轨道的初步设计。张磊等[13]通过三级微分修正完成了轨道高精度模型下求解,精度高但过程复杂。曹鹏飞等[14]针对载人登月绕月自由返回飞行任务,提出一种混合-分层轨道优化设计方法,仿真结果表明该设计方法具有求解精度高、收敛速度快等优点。陆林等[15]建立了基于近月点伪参数的两段拼接模型,采用一种考虑地球扁率修正的改进多圆锥截线法求解高精度自由返回轨道。Zhang等[16]提出了一种基于简单初值猜测的线性近似方法,可直接在高精度模型中完成地月自由返回轨道的快速解算。

载人月球探测是一项庞大复杂的航天任务,需要综合考虑各项任务指标及工程约束因素的影响,建立月面任务综合代价评估准则,以实现对不同着陆区探测效能的横向对比分析和全局评估[17]。任务周期、任务窗口以及速度增量等任务效能因素和任务光照、再入返回等工程约束是当前任务综合代价评估考虑的重点。贺波勇等[18]提出了基于双二体模型的轨道窗口存在性快速判据,将窗口存在性问题转化为含约束非线性规划问题求解。陆林等[19]提出了一种基于双重优化算法的两层串行求解策略,并通过大量仿真计算对月球返回轨道可达域、速度增量等轨道特性展开了分析。彭坤等[20]建立了一套飞行模式评价模型,从速度增量需求、飞行时间、空间环境、登月任务窗口、测控条件和任务可靠性方面对不同位置空间站的登月飞行模式进行分析和定量评价。

综上,载人月球探测飞行轨道设计方面,现有文献仅针对地月转移轨道或月球返回轨迹进行优化设计,且通过简化二体拼接模型提升轨迹优化效率,牺牲了轨道设计精度;任务综合代价评估方面,现有方法仅针对某些因素进行评估分析,缺乏多因素综合代价评估准则。因此,本文首先基于伪状态理论建立载人月球探测任务转移轨迹优化模型,实现高精度地月自由返回轨道和月球返回轨道的高效解算;在此基础上,提出了基于动态权值策略的载人月球探测任务综合代价评估方法,以2027—2037年为例,通过大量数据仿真分析,给出定量评估的动态权值取值范围,实现不同月面着陆区任务的综合代价评估,为未来开展载人月球探测任务提供参考。

1 载人月球探测任务转移轨迹设计

1.1 任务飞行模式

“人货分运、多次交会”的飞行模式具有相对较高的安全性和较小的运载火箭能力需求的优点,本文后续转移轨道设计和评估分析均以此种模式为例,针对载人飞船和着陆器的地月转移段及载人飞船的月地转移段轨迹展开。地月往返转移轨迹优化计算考虑地月空间地球和月球引力共同作用的精确动力学模型如下所示:

(1)

式中:μE为地球引力常数;r为探测器在地心惯性系下的位置矢量;μm表示月球引力常数;rmd表示探测器相对月球的位置矢量;rm表示月球在地心惯性系下的位置矢量;r,rmd分别为探测器相对地球、月球的距离;rm为月球相对地球的距离。

另外,本文分别选取了7个分布在月面低纬度及中高纬度区域的落月点作为载人月球探测任务潜在备选着陆区,其经纬度信息如表1所示。

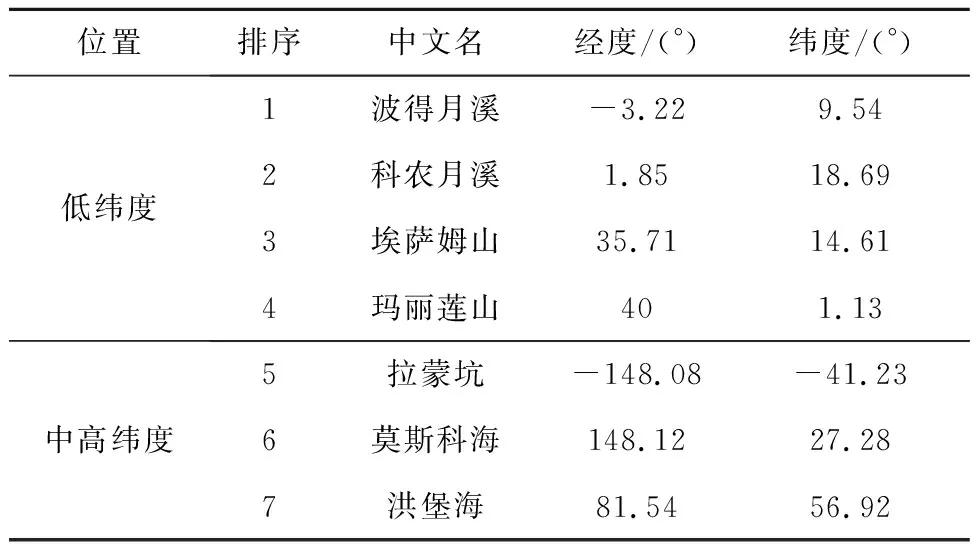
表1 载人月球探测备选着陆区经纬度信息[21]Table 1 Information of potential landing sites for manned lunar exploration[21]

1.2 着陆器地月转移轨道优化设计

在人货分运模式中,着陆器采用常规地月转移轨迹,以降低月球制动速度增量消耗,增加可行窗口。精确动力学模型考虑了地月空间三体摄动干扰,直接用于任务轨迹优化设计会导致沉重的计算负担。因此,本文采用基于伪状态理论的单步法实现各段轨迹高精度近似解算,使用自适应迭代拼接技术对各段轨迹进行拼接,该技术采用自适应参数调整策略来提高效率和鲁棒性。基于伪状态理论的地月转移轨迹优化模型如图1所示。

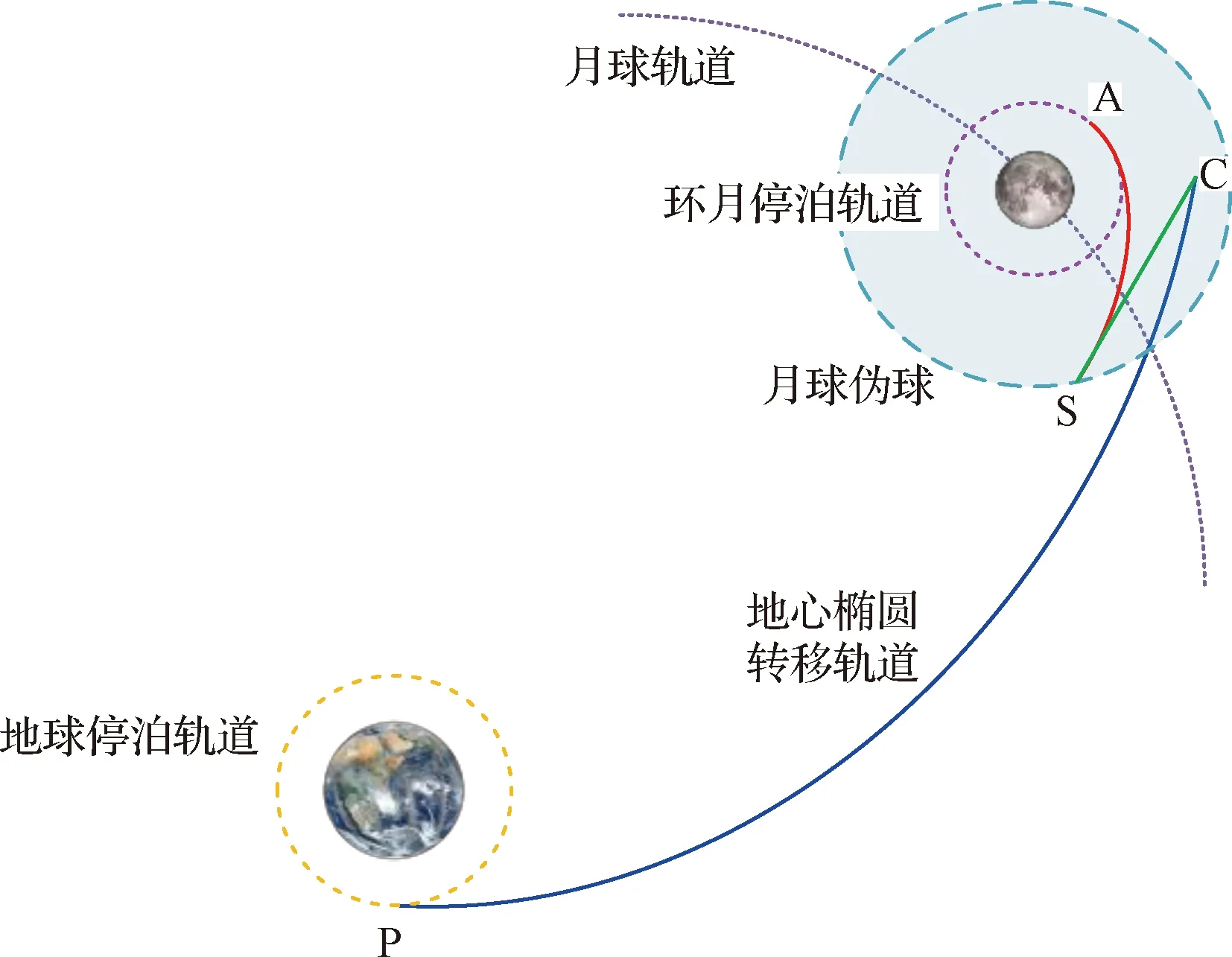
图1 基于伪状态理论的着陆器地月转移轨迹优化模型Fig.1 Optimization model of the Earth-Moon transfer trajectory of the lander based on pseudostate theory

伪状态模型中涉及的轨迹均为可解析计算的圆锥曲线(双曲线和椭圆)和直线,避免了三体动力学模型下的复杂数值积分,具有突出的计算效率和精度。伪状态模型的精度取决于伪球的半径,通常用回归时间来表示。因此,回归时间决定了基于伪状态理论的摄动引力辅助模型的近似精度,月球的最优回归时间为飞行时间的65%[22]。

对于给定的初始停泊状态(t0,rP_M,vP_M)和近月点到达时间tf,地月转移轨迹根据终端位置rC_M求解,椭圆弧的速度vC_M由兰伯特问题求解,再根据伪状态理论计算回归段的终端状态(rS_M,vS_M),从而计算接近段的实际终端状态(ra_M,va_M):

(2)

式中:Ψha表示受引力辅助天体引力支配的状态转移矩阵;ΔTd是月球的最优回归时间。

因此,只需要通过调节C点的位置矢量,就能够控制伪状态轨迹的末端位置到达目标轨道,则地月转移的速度增量为

ΔVtol=ΔVP+ΔVA=||vD_E-vP_E||+

||vA_M-vP_M||=f(t0,ttof,oepm)

(3)

即速度增量是初始时间t0、转移时间ttof和环月轨道状态oepm的函数。

环月轨道采用200 km的圆轨道。环月停泊轨道的轨道倾角由着陆区纬度和等待时间决定。不失一般性地假设着陆区的月理经纬度为(α,β),则环月轨道的轨道倾角i满足如下条件:

(4)

式中:D表示等待时间;ωM表示月球自转速度。

环月停泊轨道的升交点经度由着陆区经度和等待时间决定,满足如下条件:

(5)

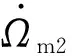
此外,本文采用三脉冲制动入轨简化模型估算月球制动捕获入轨所需速度增量。首先,在近月点施加脉冲进入环月大椭圆轨道;然后,在远月点施加第2次脉冲调整轨道面;最后,着陆器再次回到近月点时施加第3次脉冲以交会环月轨道。则近月三脉冲制动的速度增量表示为

(6)

式中:φA表示地月转移轨道与大椭圆轨道之间的夹角;rp表示近月点半径,rp=1 938 km;aZ和eZ分别表示大椭圆轨道的半长轴和偏心率,计算如下

(7)

式中:T表示大椭圆轨道周期,为不失一般性,本文设定T=0.5 d。

因此,对于选定的月球着陆点,地月转移的总速度增量表示为

ΔVtol=ΔVP+ΔV1+ΔV2+ΔV3=f(t0,ttof,u)

(8)

综上所述,着陆器转移轨迹优化问题最终被建模为地月转移时间窗口t0、飞行时间ttof和环月轨道的近月点角距u的参数寻优问题。

1.3 载人飞船地月转移轨道优化设计

不同于着陆器地月转移轨道,载人飞船为了确保航天器的安全,往往采用地月自由返回轨道,以确保在飞船失去动力时仍然能够返回地球。地月自由返回轨道本质上是利用月球引力辅助调整返程轨道,瞄准地球。本文将月球自由返回轨道优化设计问题建模为月球引力辅助轨迹优化问题,如图2所示。为匹配指定位置A(表示为rGA)的接近段和逃逸段轨迹,需要在指定位置执行脉冲机动以修正接近段和逃逸段。

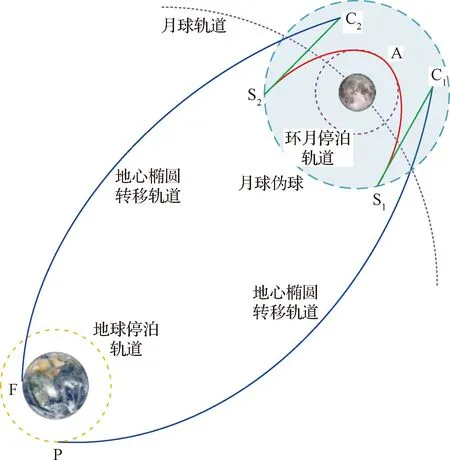
图2 地月转移自由返回轨迹优化模型Fig.2 Optimization model for the Earth-Moon free-return trajectory

对于具有给定近月点到达时间和环月轨道,其所需的速度增量主要由月球引力辅助匹配位置决定。在基于伪状态理论的摄动引力辅助模型中,初始状态(t0,R0,V0)和近月点时刻tGA是给定的,接近段用接近段主椭圆弧的终点位置rae求解。

中心椭圆弧的速度由Lambert问题求解,再根据伪状态理论计算接近段的实际终端状态(rGAa,vGAa)。近月点A作为逃逸段的初始位置,必须修正初始速度以保证逃逸段能够到达期望位置Rf。当初始位置和速度(rGAd,vGAd)已知时,逃逸中心椭圆弧的初始位置和速度(rde,vde)可由下列方程求解。

(9)

式中:rGAd和vGAd是逃逸段的初始位置和速度;Ψhd表示由月球引力主导的双曲线轨迹的状态转移矩阵。

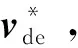
(10)

地月自由返回轨道优化中近月点必须位于设定的环月轨道上,因此,一般通过控制近地点角距和返程飞行时间使速度增量消耗最小。因此,目标函数定义为

J=||ΔvGA||+||ΔV0||+||ΔVf||=||vGAd-vGAa||+||Va0-V0||+||Vf-Vdf||=f(u,ttof2)

(11)

式中:u是环月轨道的近月点角距;ttof2是月球返回轨道飞行时间。

综上所述,接近段和逃逸段的最佳匹配位置使用MATLAB中的默认工具fmincon进行优化。

1.4 月球返回轨道优化设计

月球返回轨道可以被视为地月转移轨道的逆过程,包括逃逸准备段和月地转移段,如图3所示。逃逸准备段是航天器通过三脉冲转移调整轨道面和相角以降低月球逃逸所需速度增量。月地转移段是航天器从准备段末端转移至地球大气层边界的过程。

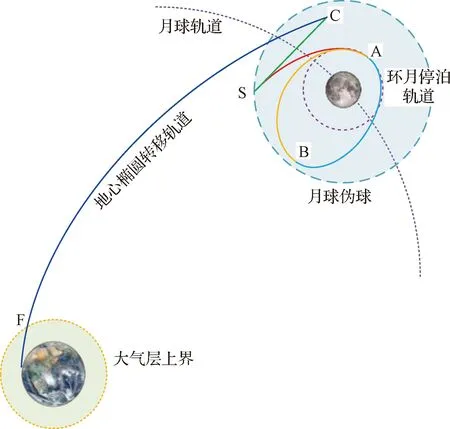
图3 月球返回轨道伪状态轨迹优化模型Fig.3 Optimization model for the Moon-Earth return trajectory via pesudostate theory

对于逃逸准备段,航天器首先在近月点施加脉冲进入环月大椭圆轨道;然后,在远月点施加第2次脉冲调整轨道面,最后,航天器再次回到近月点时施加第3次脉冲以进入月地转移轨道。月球三脉冲逃逸的速度增量可表示为

(12)

式中:φD表示月地转移轨道与大椭圆轨道之间的夹角。

月地转移过程是地月转移的逆过程,详细计算过程此处不再赘述。为确保载人飞船定点返回,对再入点位置和再入速度进行约束,以确保载人飞船的再入航程满足约束。再入点位置和再入速度约束的具体处理过程详见文献[23]。

2 载人月球探测任务综合代价评估准则

本文考虑的评价指标分为效能评价指标和工程约束指标两类。根据高精度动力学模型下计算所得的窗口信息与相关数据分析,构建出各评价指标的权值函数。

2.1 效能评价指标参数分析

2.1.1速度增量指标参数

根据前文的转移轨迹优化计算方法,以波得月溪着陆区2027年3月14日的可行发射窗口为例,航天器出发时间和转移飞行时间能量消耗呈现出规律的环状分布,如图4所示。对于同样的出发时间,适当增加转移飞行时间可以降低速度增量的消耗,但超过一定阈值之后,长时间的转移飞行会导致速度增量消耗增加。考虑到总飞行时间不超过4天的计算约束及其他轨道约束,最终最优发射窗口的优化结果出现在期望的速度增量低谷处。

由于载人月球探测任务过程复杂、历时长,综合代价评估更注重在满足任务所有约束条件前提下,各阶段飞行轨道衔接匹配设计问题。根据对可行发射窗口宽度的分析可知,较小的速度增量发射窗口在备份能力上也有比较优秀的表现,因此,可将速度增量进行分段,作为综合代价评估模型的一项强影响指标。

从上图中可以看出,速度增量Δv大于1.7 km/s之后会产生突变,因此可将速度增量Δv= 1.7 km/s作为分段点,并对拼接点进行平滑处理防止出现权值跳变。根据载人月球探测任务的总速度增量要求,限制参与评价的窗口总速度增量均小于2 km/s。因此,可给出速度增量指标参数函数如下:

(13)

式中:Δv表示载人月球探测任务的总速度增量。

2.1.2转移时长指标参数

不失一般性,设定地月发射C3不超过20 km2/s2,满足发射场经纬度及发射约束,转移飞行时间上限为4天,采用遗传算法逐天搜索并筛除近月点拼接速度增量不为零的点,即不满足自由返回轨道约束要求的窗口,限制地月转移出发段速度增量小于0.935 km/s。最后,表1中列出的着陆区的可行发射窗口优化结果如图5所示,拉蒙坑和洪堡海着陆区由于纬度太高,无法找到满足任务约束的可行窗口。

由上图可知,不同着陆区的地月转移时间多分布在2～3天内,每年较为集中的可行发射窗口对应的地月转移时间基本呈现出先增后减的趋势,但峰值月份略有不同,在3月至5月不同的月面着陆区都出现了较多的可行发射窗口。另外,不同着陆区均有一定的重合窗口出现,地月转移时间呈现出相似的变化趋势。

在满足自由返回轨道约束的基础上,进一步对初步筛选过的地月转移轨道展开月球返回轨道优化计算,限制总转移速度增量小于1.97 km/s,最终获得的可行发射窗口具体结果如图6所示。

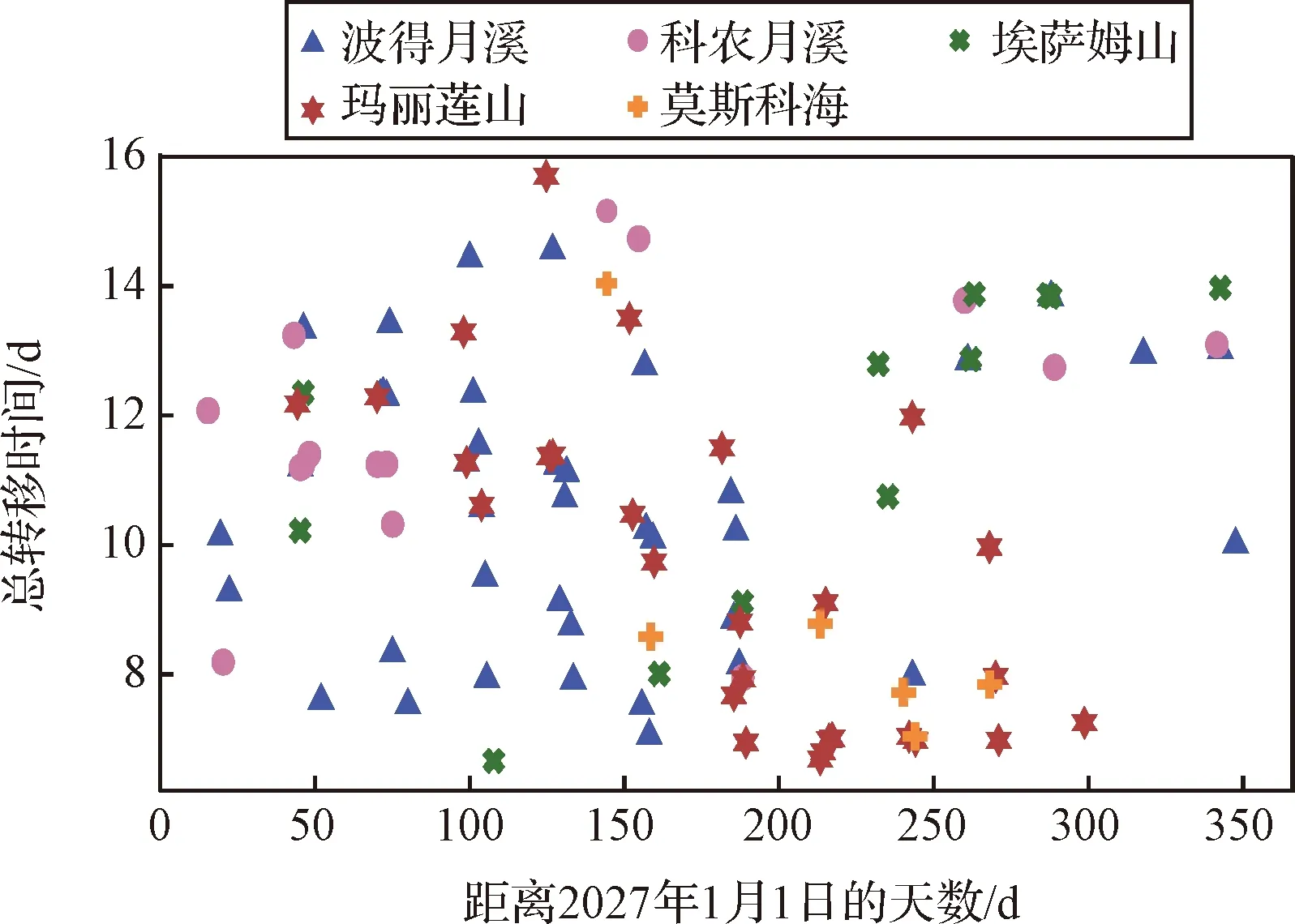
图6 月面着陆区2027年返回陆上着陆场可行发射窗口总转移时间分布Fig.6 Feasible launch window distribution of the lunar landing sites in 2027 (returning to land-based landing sites)

对于整个载人月球探测任务而言,总任务时长在8～14天范围内呈周期性变化,其中每年的第200～250天内分布的可行窗口比较少,总任务时长较短的窗口多分布在每年的上半年,总任务时长较长的窗口多分布在每年的下半年。

本文在筛选可行发射窗口初期优先筛选了符合总转移时间要求的出发窗口,用于后续其他约束下的轨道优化计算,但考虑到较短的转移时长对可行发射窗口的月面停留时长会产生一定的影响,进而影响整个任务窗口的备份能力和工程代价,因此,给出转移时长指标参数函数如下:

(14)

式中:ttof0表示总任务转移时长。

2.1.3任务窗口指标参数

为保证发射窗口的质量,考虑到两次任务都可能存在推迟发射情况,本文对优化计算出所有可行窗口的宽度展开分析。采用数值延拓的基本思想,对优化得到的可行发射窗口进行延拓分析,分别在原本的最优出发时刻上向前、向后延拓0.5小时,采用遗传算法及第1节所述的转移轨道计算方法对每个可行窗口的延拓解进行优化计算。以波得月溪2027年最优发射窗口前后延拓0.5小时可行发射窗口分布为例,从转移出发的速度增量消耗、飞行时间两个维度,对可行发射窗口的延拓解进行评估分析,具体结果如图7所示。

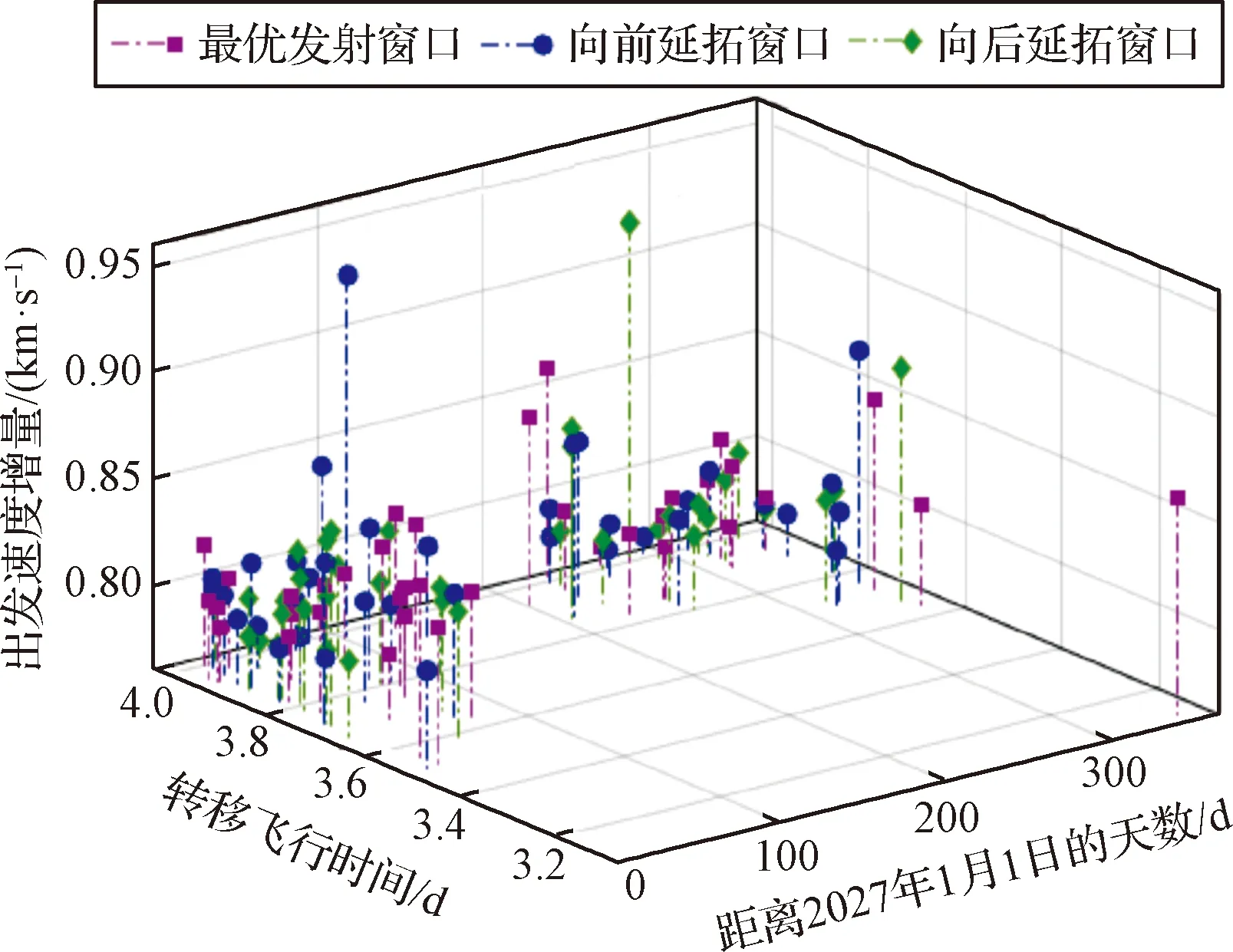
图7 波得月溪2027年可行发射窗口的出发时刻、飞行时间与速度增量关系图Fig.7 Relations of departure time, flight time and velocity increment of the feasible launch windows of Rimae Bode in 2027

分析可知,对于每一个最优发射窗口,在出发时刻上前后进行0.5小时的延拓,对速度增量与转移时间的分布影响波动比较小,仍在约束要求范围内,且最优发射窗口多满足速度增量及转移时间综合比较小的情况,相较于延拓解,最优解对其他约束的符合度更好。

表2给出了7个候选着陆区所有可行发射窗口满足延拓0.5小时约束的情况分布,可以看出,月面着陆区除极少数窗口以外,计算获得的可行发射窗口均满足宽度要求,具备推迟发射的能力。不满足延拓要求的窗口其本身已临近总速度增量极限,其延拓解均会超出速度增量约束,故不符合窗口宽度要求。而出于对载人月球探测任务的安全性考虑,中高纬度着陆区的窗口宽度一般较小,不符合本文的约束要求。

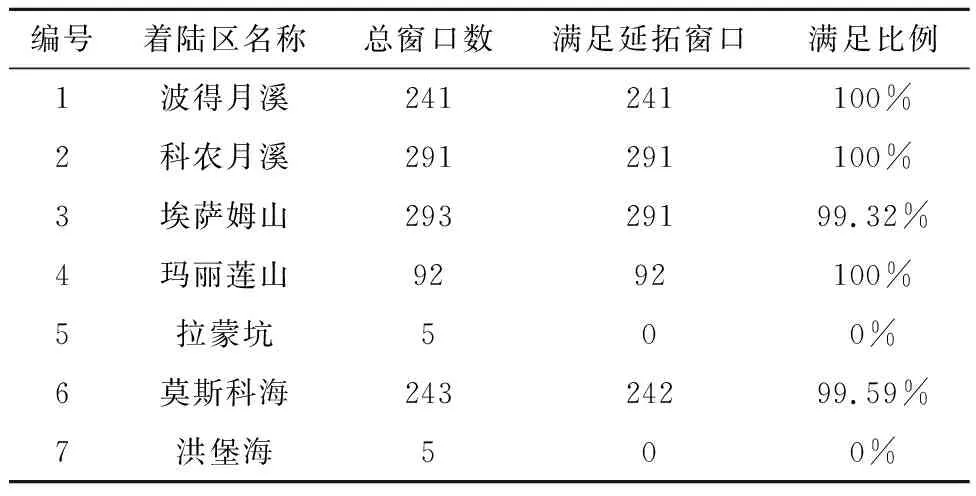
表2 月面着陆区窗口满足延拓0.5小时约束情况分布Table 2 Mission windows with 0.5-hour delayed launch capability of the lunar landing sites

为保证发射窗口的质量,不仅需要对优化计算所得的所有可行窗口宽度展开分析,本文还对所有可行窗口的备份能力进行了分析评估。

在所有候选窗口中挑选连续2天、连续2个月出现过的可行发射窗口。以波得月溪2027年最优发射窗口连续2天、连续2个月的可行发射窗口分布为例,具体结果如图8所示。

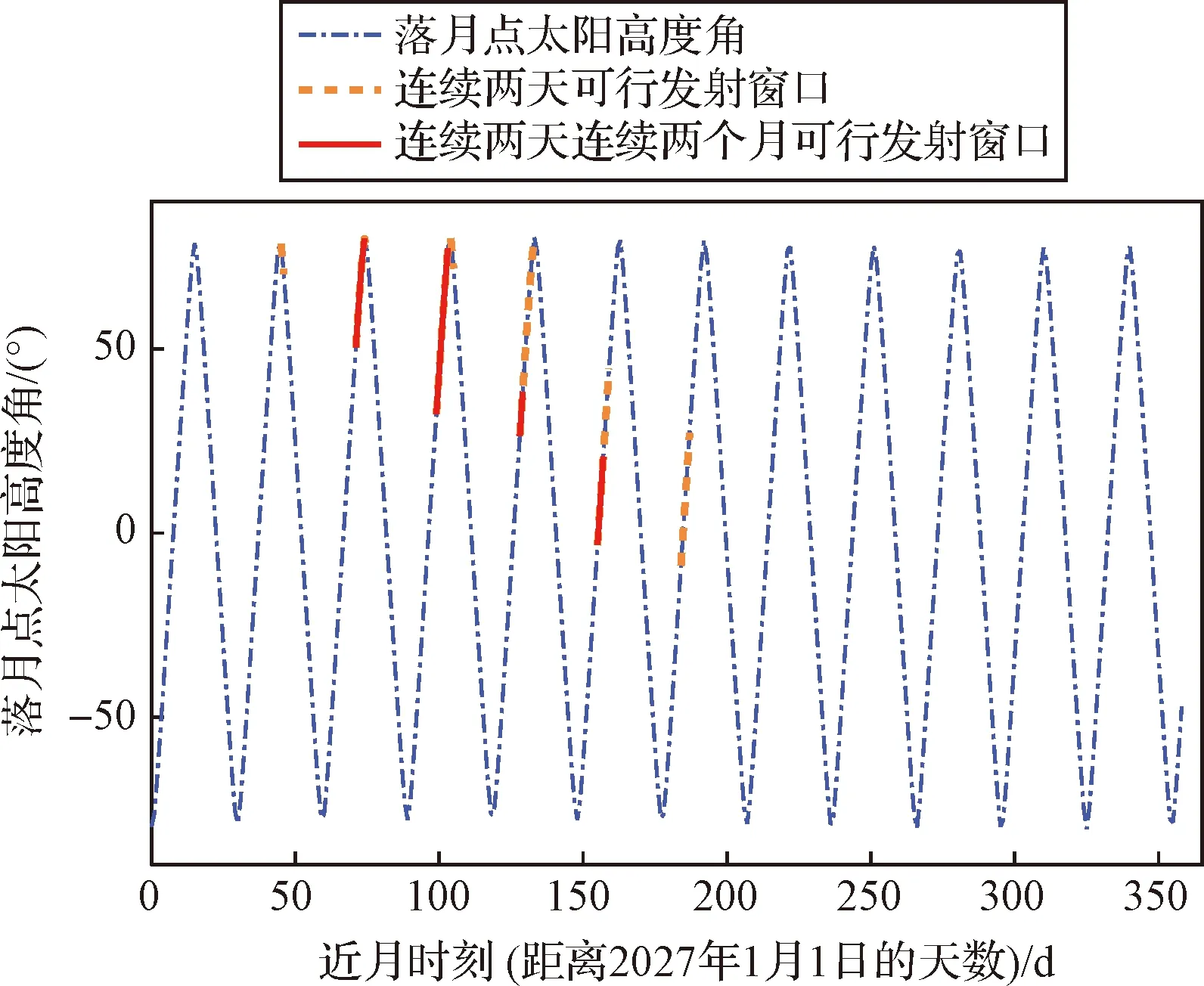
图8 波得月溪2027年连续2天、连续2个月的可行发射窗口分布Fig.8 Feasible launch window distribution of Rimae Bode with two consecutive days and two consecutive months in 2027

分析波得月溪2027年连续可行发射窗口分布图可知,连续窗口出现呈一定规律,出现的时间间隔大致相等,周期约为20～30天,并且连续窗口均出现在2027年上半年,近月时刻多为正午之前,此时太阳高度角尚未达到峰值。图9给出了月面着陆区返回陆上着陆场及返回海上着陆场的连续2天及连续2个月的可行发射窗口数目。

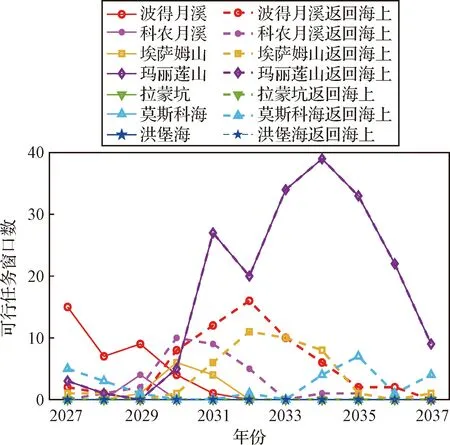
图9 月面着陆区返回陆上着陆场及海上着陆场的连续2天、连续2个月可行发射窗口数目Fig.9 The number of feasible launch windows of the lunar landing sites with two consecutive days and two consecutive months (returning to land-based and sea-based landing sites)

由上图可知,波得月溪等位于月球北半球的着陆区,连续窗口出现在2033年之前;而对于赤道附近的玛丽莲山着陆区,每年均会出现可行发射窗口,且数量远超出其他着陆区。

对比上图可知,月面着陆区返回海上着陆场相较于返回陆上着陆场的可行发射窗口分布,总窗口数目更多,窗口出现的年份分布也更加广泛。由于陆上着陆场与海上着陆场的纬度区别较大,海上应急着陆窗口为载人月球探测任务的可行窗口提供了很大的扩展空间,因此,海上着陆场可作为陆上着陆场的补充增加窗口。

本文采用数值延拓的基本思想,对优化获得的可行发射窗口进行延拓分析,并对所有连续2天可行窗口的连续2个月窗口分布进行了分析评估。给出任务窗口指标参数函数如下:

Gw=1+w

(15)

式中:w表示任务窗口权值,当仅满足连续2天的任务窗口时取值为0.6;同时满足连续2天和2个月的窗口时取值为1。

2.1.4月面探测停留时长指标参数

对于考虑再入返回约束和总任务时长约束的月球返回轨道,月面探测的停留时长直接影响了月球返回的转移时长及返回着陆范围。但考虑到月面科考工作的不确定性,本文在设计的月面活动时间3天的基础上,利用数值延拓的思想,对可行发射窗口分别延拓计算了月面停留时间延长到4～7天的可行窗口分布。以波得月溪着陆区为例,从图10中可看出,随着月面停留时间的延长,月球返回的速度增量均有一定的增加,对于转移出发飞行时间较长的窗口,月面停留时间较长会导致该类窗口无法满足总飞行时间约束。

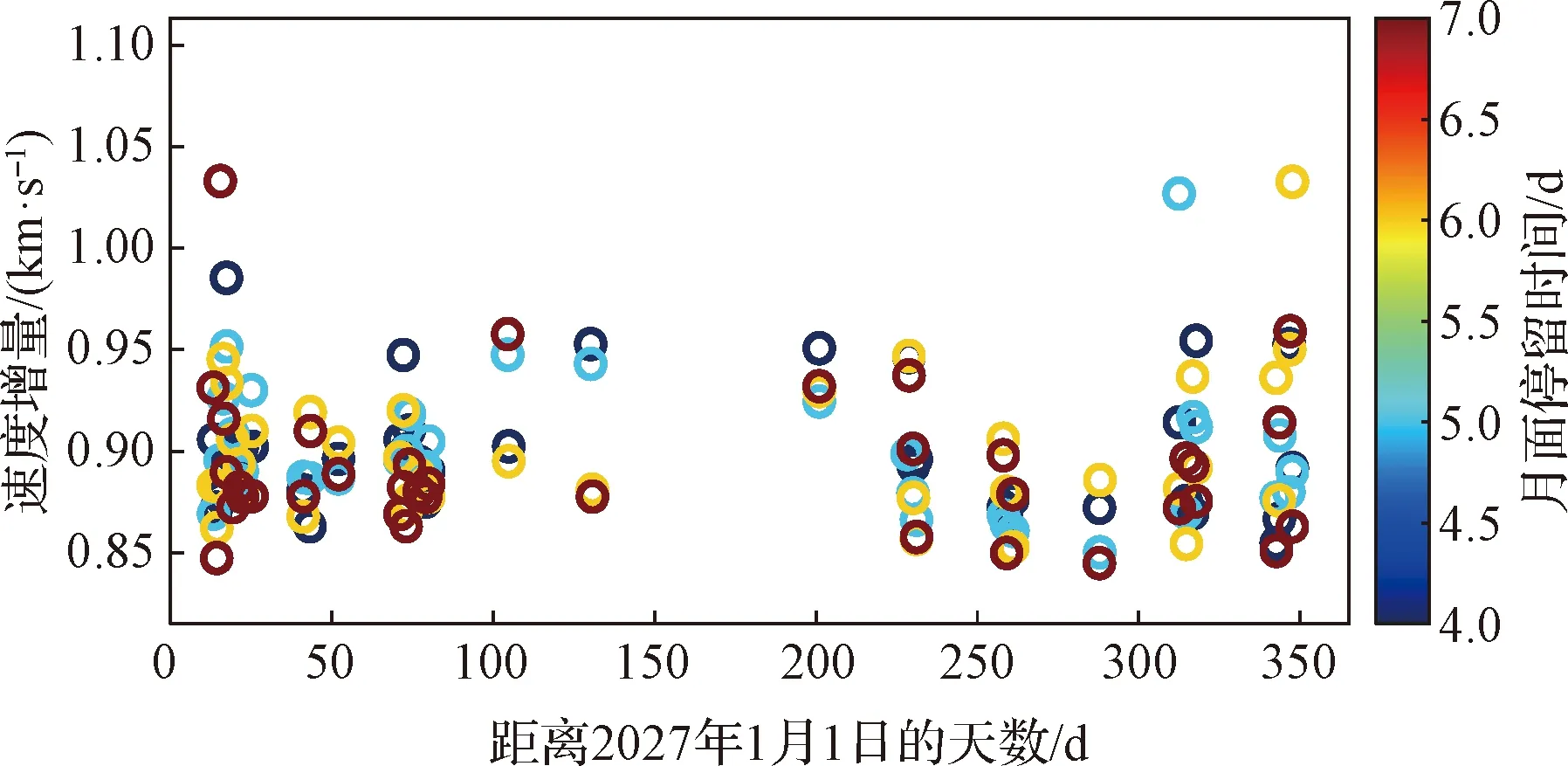
图10 波得月溪2027年返回陆上着陆场的月面停留时长延拓窗口速度增量分布Fig.10 Velocity increments of extending mission period of Rimae Bode in 2027 (returning to the land-based landing sites)

因此,给出月面探测停留时长指标参数函数如下:

GST=1+κtST

(16)

式中:权值参数κ的取值如表3所示。

表3 月面探测停留时长指标参数κ取值信息Table 3 Value range of κ, the parameter of lunar detection residence duration

2.1.5区域科学价值指标参数

在前期工作获得的精选着陆区中[24-25],选取了7个位于月面低纬度及中高纬度的区域,其科学探测价值排序结果如表4所示。

表4 月球潜在着陆区科学探测价值排序Table 4 The scientific exploration value ranking of potential landing sites on the Moon

根据7个着陆区的科学探测价值排序,可得出月面低纬度及中高纬度着陆区区域科学价值指标参数的权值函数,从而构造综合代价评估模型。着陆区科学价值指标GS的权值k的取值区间为[1,7]的整数,则区域科学价值指标参数函数定义如下:

GS=1+k

(17)

2.2 工程约束指标参数分析

2.2.1光照条件约束参数

载人航天任务中,为保障通信电力供给充足,约束月面着陆器落月时刻的阳光入射角(太阳光和月面的夹角)范围为5°～90°。由于太阳高度角约束与飞行轨道无关、只与月面停留时间和月面着陆点位置相关,因此,可优先判断太阳高度角约束。对月面着陆区波得月溪的月面光照条件分析可知,2027年满足太阳高度角约束的发射窗口呈现规律的周期性变化,周期约为1个月,总窗口数约占全年的一半。图11给出了波得月溪2027年载人月球探测任务符合光照约束的窗口分布。

所有约束中,月面动力下降时刻太阳入射角由着陆区域在月固系中经纬度决定,任务事先往往给定着陆区,这时,动力下降时刻太阳入射角约束只能通过窗口调节。因此,月面动力下降窗口受到强约束。

本文在轨道设计初期,优先筛选了符合轨道太阳高度角约束的出发窗口用于后续其他约束下的轨道优化计算,因此,本文给出的可行发射窗口均满足抵月时刻对应的太阳高度角约束,故该项工程约束指标不计入综合代价评估准则模型中。

2.2.2返回着陆约束参数

根据载人航天任务的返回着陆原则,在允许的条件下优选陆上着陆场。为便于开展航天员搜救,返回陆上着陆场时间尽量选在白天,返回海上着陆场的时间要求在白天。此外,本文考虑的再入状态约束包括再入角约束为-6° ± 0.2°,再入航程约束为3 000～8 000 km。

对于载人月球探测任务,月球返回轨道选择不同的目标着陆场,对可行发射窗口的分布规律会造成较大的影响。以位于月球北半球的波得月溪着陆区为例,由图12可知,返回陆上着陆场的可行发射窗口出现在2033年之前,但返回海上着陆场的可行发射窗口在2027—2037年均有分布。

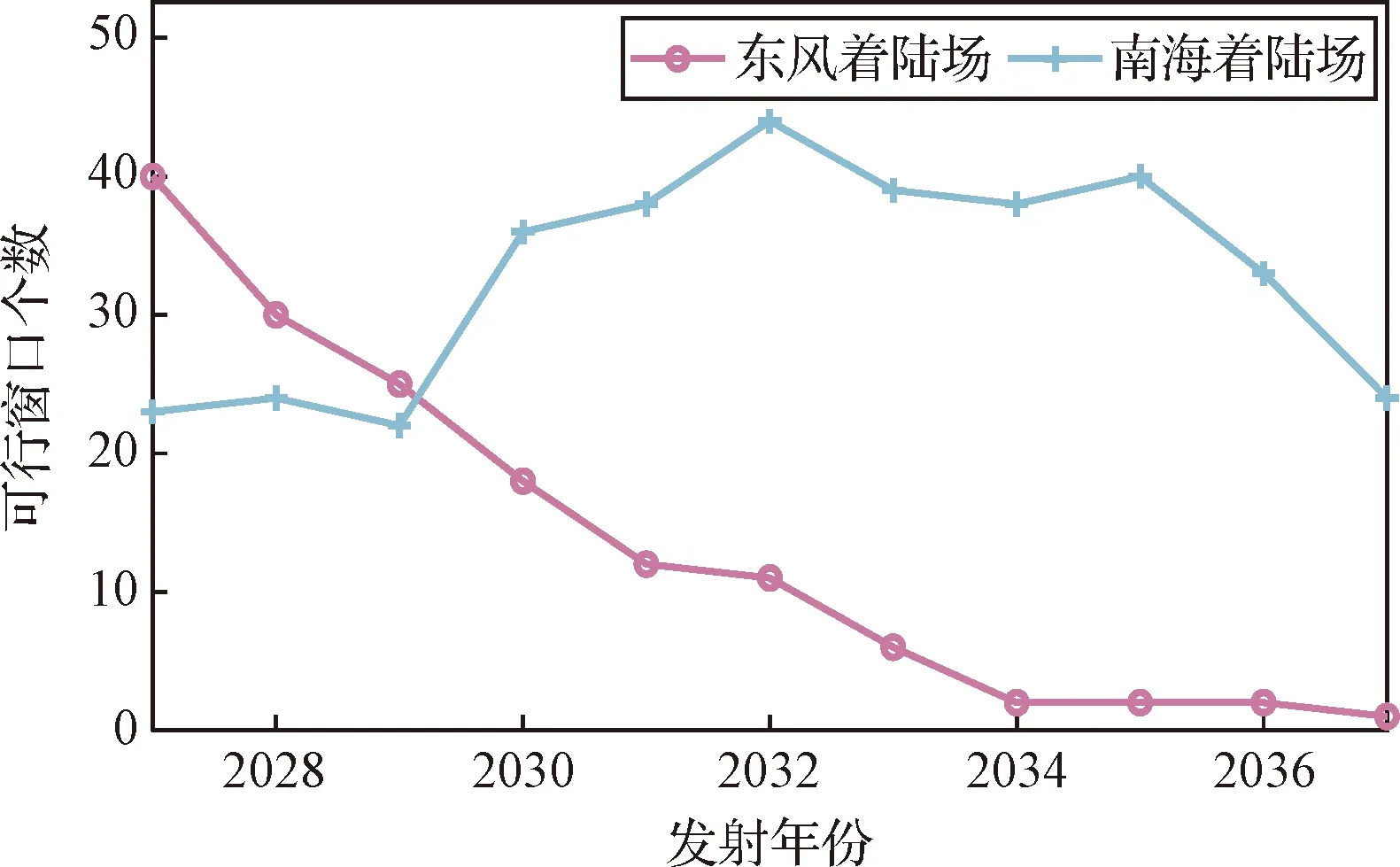
图12 波得月溪2027—2037年返回不同着陆场的可行发射窗口分布Fig.12 The feasible launch window distribution of Rimae Bode with returning to different landing sites from 2027 to 2037

因此,返回海上着陆场的可行解可作为载人月球探测任务返回着陆的补充窗口,该返回条件也可作为权值影响因素加入评价指标中。返回着陆约束指标参数函数定义如下:

(18)

式中:xdf和xsea分别表示返回陆上着陆场和海上着陆场的窗口数量;κsea表示返回海上的权值系数,当返回海上的时间在适宜返回搜救期间时,取值0.5,否则取值0.3。

2.3 载人月球探测任务综合代价评估准则模型

为满足不同目标着陆区以及时长探测任务评估需求,实现各项任务指标影响的综合评估,需要综合考虑各项指标及约束因素的影响,基于加权的方式构建综合代价评估准则模型,建立通用性的评价准则体系。本文首先利用高精度模型对各项评价指标分别进行计算,再对各项因素及约束进行加权综合,满足低纬度及中高纬度着陆区的载人月球探测任务工程约束与代价的综合分析需求。

本文考虑的评价指标包括效能评价指标和工程约束指标两类。主要为轨道转移消耗(转移速度增量消耗、转移时长等)、任务窗口(窗口数量、窗口时间间隔、窗口备份能力等)、月面探测(月面候选区域分值、月面停留时长等);约束则包括各类光照时长约束、返回着陆约束等因素。本文通过对各项指标进行加权综合,构建综合代价评估指标G,其形式如下所示:

(Cw)i(Gw)i]+CSGS+CSTGST+CRGR

(19)

式中:C和G分别代表权值以及指标参数;下标“Δv”表示转移速度增量;“tof”表示转移时长;“w”表示任务窗口数量;“S”表示月面候选区域的分值;“ST”表示月面停留时长;“R”表示任务窗口返回着陆约束;k代表可行的任务窗口数量。

考虑到不同指标参数的量纲不同,首先将效能评价指标参数和工程约束指标参数的指标类型转换为统一的极小值指标,再对指标参数函数进行标准化处理,便于构建综合代价评估准则模型。指标参数函数的取值区间由对应指标相应约束范围来决定,其中任务窗口指标参数的取值区间为符合全部飞行约束的窗口总数。

对于本文建立的极大型指标,可采用下式进行极小化处理,相应的参数函数取值区间如表5所示。

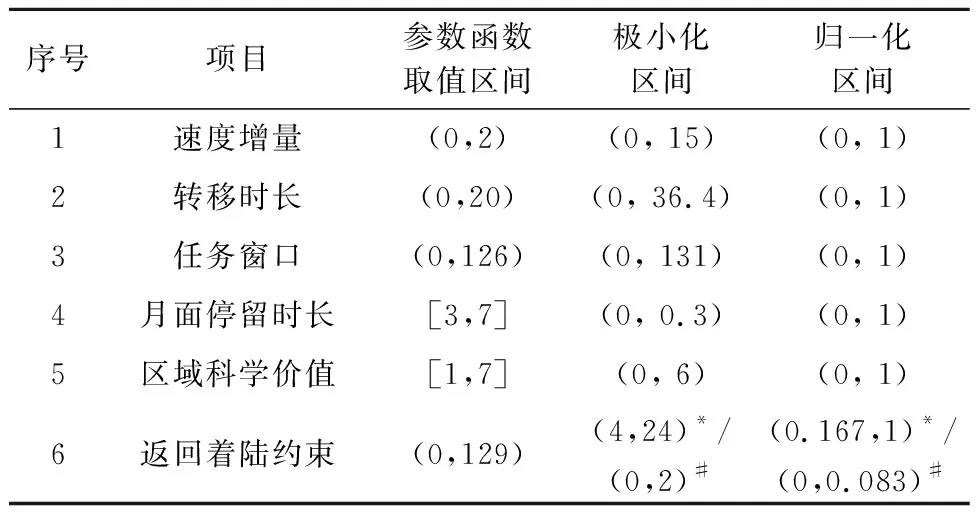
表5 指标参数的权值区间、极小化区间及归一化区间Table 5 Weight range, minimization range, and normalization range for the performance indicators

(20)

由此可将评价指标参数转换极小型指标形式{x′ij},i=1, 2, … ,n; 1≤j≤6。然后,通过下式做极差变化将数据标准化:

(21)

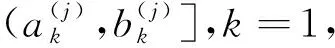
表5给出了效能评价指标参数和工程约束指标参数的权值区间、极小化区间及归一化区间。

考虑到评价指标的“质差”与“量差”,在确定综合代价评估指标时,既要体现同类型指标的数量差异,也要体现不同类型指标之间的差异。因此需要给不同指标参数再次加权,最终构建出载人月球探测任务综合代价评估准则模型。考虑到中高纬度着陆区具有较高的探索价值,可适当放宽对其速度增量等任务约束要求,根据工程约束及评价准则优先级,对低纬度及中高纬度着陆区建立不同的综合代价评估准则模型,结合实际问题具体分析,可分别给出不同类型指标的加权值,如表6所示。

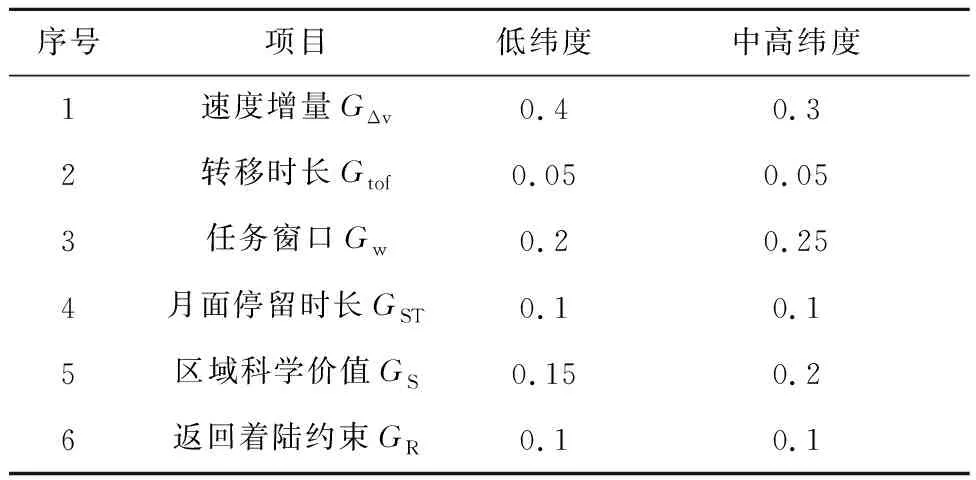
表6 月面着陆区不同指标参数分类加权的权值Table 6 Weights of classification weighting of different index parameters for lunar landing sites

至此,已经建立起低纬度及中高纬度着陆区的综合代价评估准则模型,每个被评价对象的j个属性都有N组样本值,并已完成标准化处理,将其代入综合代价评估准则模型中计算可得综合代价评估值矩阵XG,并由此得出不同着陆区的综合代价评估总排序方案。

3 数值仿真结果

基于本文建立的载人月球探测任务综合代价评估准则体系及各项指标参数对应的函数模型,对低纬度及中高纬度区域的7个着陆区展开综合代价评估。将载人月球探测飞行轨迹优化结果依次代入载人月球探测任务低纬度及中高纬度着陆区综合代价评估准则模型,可计算出每个被评价着陆区的综合代价评估矩阵XG,从而得到不同着陆区的综合代价评估总排序方案。

表7给出了低纬度及中高纬度着陆区不同指标参数加权后的综合评估矩阵,该矩阵为极小化、归一化之后的标准矩阵。根据排序结果可知,月面着陆区的综合代价评估结果基本与其科学价值排序相符,其中玛丽莲山因为其任务窗口与转移时长参数指标相对较高,从而其综合评价排序较为靠前;而中高纬度着陆区,因拉蒙坑和洪堡海相对位置较难到达,可行窗口宽度不足,故其为不满足当前任务约束的着陆区,因此排序较末,而莫斯科海因其速度增量、任务窗口及返回着陆指标参数都远优于其他中高纬度备选着陆区,故其综合评估排序较优。

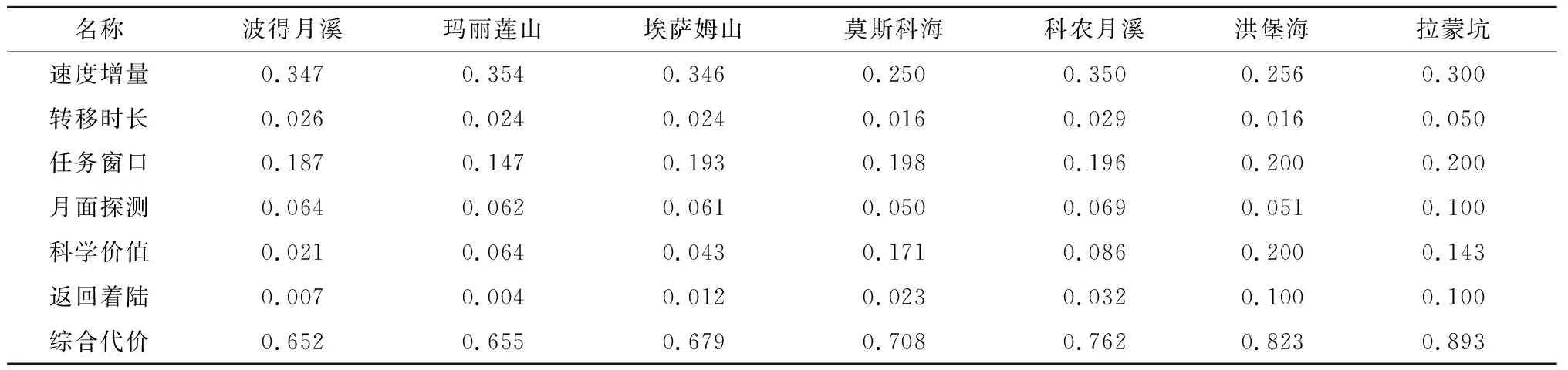
表7 月面着陆区加权后的综合评估矩阵Table 7 Weighted comprehensive assessment matrix of the lunar landing sites

4 结 论

本文针对载人月球探测任务飞行轨迹进行建模,引入基于伪状态理论的单步法实现高精度摄动轨迹的快速解算,改善飞行轨迹优化效率和精度;在此基础上,应用动态权值策略建立了综合代价评估准则模型,综合考虑各飞行轨迹的效能评价指标和工程约束指标。应用本文所提方法对文中列举的7个月面着陆区载人登月任务进行了量化评估,验证了所提方法的可行性。本文的仿真结果仅可作为综合评估方法的参考,具体指标参数的取值区间和权值的选取需要根据实际工程实施等多方面因素去权衡决定。载人登月着陆区的选择涉及到科学目标与任务分析等多项关键环节,如何将各种耦合工程约束进行标准量化评估、建立通用任务评估体系是需要进一步深入研究的问题。